Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.

792 VId. Applications: Simulation of Thermofluid Systems
the inter-nodal flow rates. Node k may also receive flow from external sources
(shown by subscript x), such as safety injection. This node may also discharge
flow if a pipe break (shown with subscript B) happens to occur at this node. Not
all these flow rates exist simultaneously or for all the nodes. However, we are
considering them for the sake of generality. The conservation equation of mass,
Equation IIa.5.1 for node k becomes:
¦¦
−+
¦
−=
kBkxkeki
k
mmmm
dt
dm
)()()()(
VId.3.1
Similarly, the conservation equation of energy, Equation IIa.6.4-1 for the node be-
comes:
¦¦
+
¦
+−+
¦
−=
RCSkkkBkxxkkekii
kk
PQhmhmhmhm
dt
hmd
V)()()(
)(
VId.3.2
Note that the work term includes only the pressure work as there is no shaft work
and the shear work is ignored. Taking the derivative of the left side, substituting
from the conservation equation of mass, and rearranging, yields:
[][]
RCSkkxkxkxkikkiikk
PcQhmhmmhhmhm
V)()()()( +
¦
+
¦¦
−−
¦
−
¦
=
VId.3.3
where c in Equation VId.3.3 is a conversion factor. We now use the volume con-
straint for node k, given the fact that V
k
remains constant hence, dV
k
/dt = 0:
()
0vvv
V
=+==
kkkkkk
k
mmm
dt
d
dt
d
The derivatives can be expanded in terms of the RCS pressure (
RCS
P ) and the
node enthalpy (h
k
):
0
vv
v =
¸
¸
¹
·
¨
¨
©
§
++
RCS
h
k
k
P
k
k
kkk
P
P
h
h
mm
k
RCS
∂
∂
∂
∂
VId.3.4
Substitute from Equations VId.3.1 and VId.3.3, we obtain:
»
¼
º
«
¬
ª
¦
+
¦
−+
¦
−
=++
¦
−
¦
+
¦
−
kxx
k
k
kx
k
k
kk
k
k
k
kkB
RCS
k
k
k
k
kkekkii
k
k
ki
k
k
kk
hm
h
m
h
hQ
h
m
P
P
m
h
cmhm
h
m
h
h
)(
v
)()
v
v(
v
v)(
)
vv
V()(v)(
v
)()
v
v(
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
VId.3.5
3. Simplified PWR Model 793
This is the general form of the mass-energy algorithm for loops using an integral
momentum equation. In this relation, the unknowns are inter-nodal flow rates and
RCS pressure. These can be determined for specified break flow rate, rate of heat
transfer to the node, and the external flow rates and enthalpies.
3.1. Determination of Nodal Flow Rates In a One Loop PWR
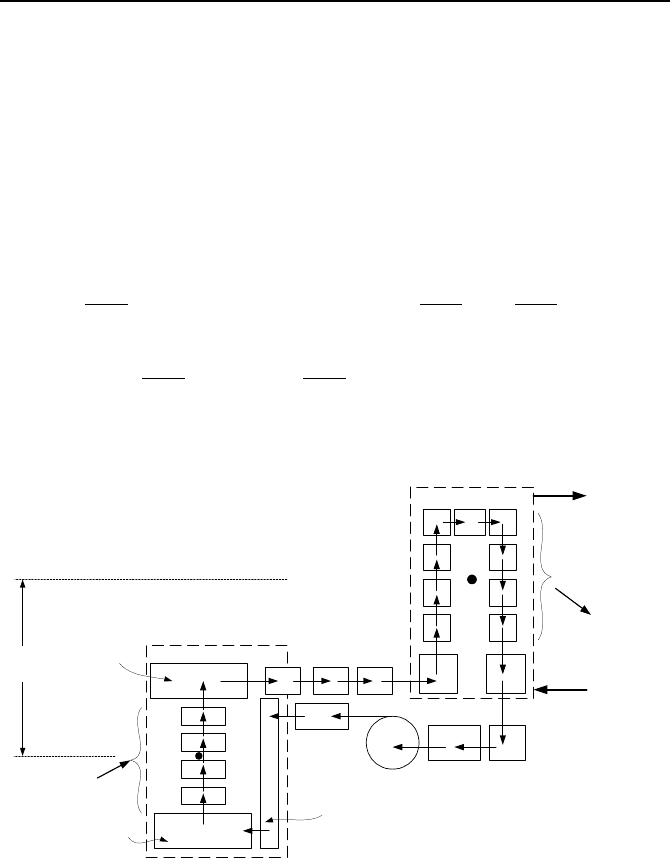
To demonstrate the application of the mass-energy algorithm, Equation VId.3.5 is
applied to a one-loop PWR as shown in Figure VId.3.2. By using the donor cell
concept, the algorithm simplifies to:
»
»
¼
º
«
«
¬
ª
¦
¸
¸
¹
·
¨
¨
©
§
−−+
¦
−
=
¸
¸
¹
·
¨
¨
©
§
++−
»
¼
º
«
¬
ª
−+
−−
kxkx
k
k
k
k
k
kkB
RCS
k
k
k
k
kkkkkk
k
k
k
mhh
h
Q
h
m
P
P
m
h
cmmhh
h
)()(
v
v
v
v)(
vv
Vv)(
v
v
11
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
VId.3.6
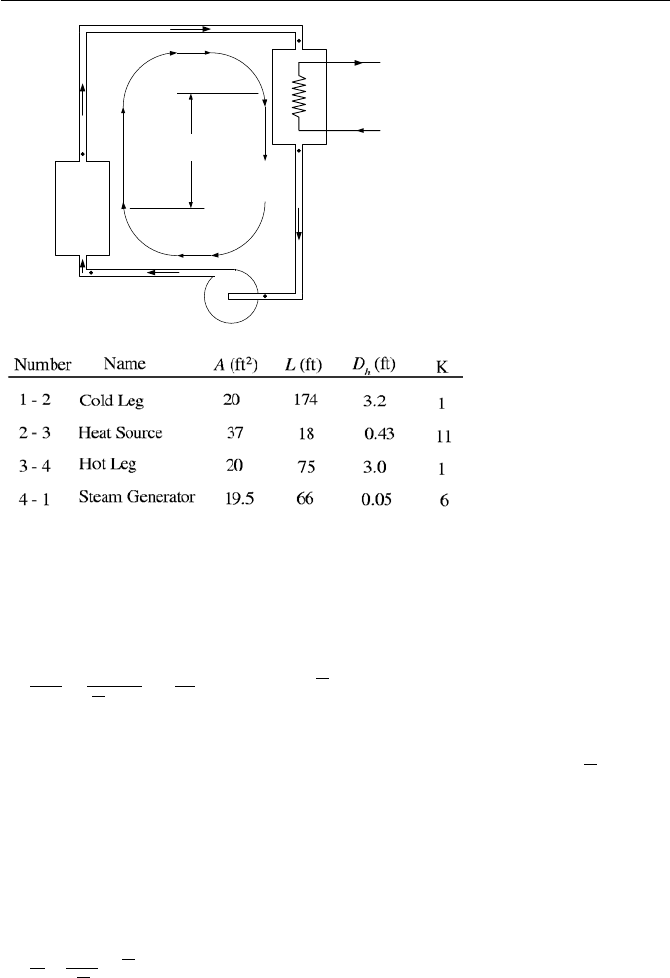
Recator Vessel
Hot Leg
RCP
Cold Leg
Cold Leg
Steam Generator (SG)
1
2
3
4
5
6
7
n - 1n
SG Tube Nodes
Core Nodes
Upper Head
Lower Plenum
Downcomer
H
th
Feedwater
Steam
Q
Q
Figure VId.3.2. A one-loop PWR, obtained by collapsing all the loops into one loop
Equation VId.3.6 can be simply shown as:
kRCSkkkkk
Pmm
εδγη
=++
−
1
where the coefficients
η
k
,
γ
k
,
δ
k
, and
ε
k
in this equation represent:

794 VId. Applications: Simulation of Thermofluid Systems
)(
v
v
1 kk
k
k
kk
hh
h
−+=
−
∂
∂
η
,
kk
v−=
γ
,
P
m
h
c
k
k
k
k
kk
∂
∂
∂
∂
δ
vv
V +=
, and
k
ε
=
()
¿
¾
½
¯
®
¦
»
¼
º
«
¬
ª
−++
¦
−
k
xkx
k
k
kk
k
k
kkB
mhh
h
Q
h
m
)(
v
v
v
v)(
∂
∂
∂
∂
We start from the discharge section of the cold leg as node 1. In this case, the
flow entering this node is from the reactor coolant pump (RCP). Applying the
mass-energy algorithm to all n nodes of the RCS, the following matrix equation is
obtained:
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
¬
ª
−−
nn
nn
δγ
δγ
δγη
δγη
δγη
δγ
"
#####
##%####
"
"
"
"
0000
000
000
000
0000
11
444
333
222
11
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
¬
ª
−
RCS
n
P
m
m
m
m
m
#
1
4
3
2
1
=
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
¬
ª
−
−
RCPnn
RCP
m
m
#
#
γε
ε
ε
ε
ηε
4
3
2
11
VId.3.7
At any time step, the thermodynamic properties and their derivatives are obtained
from the equation of state by having the two independent variables of pressure and
enthalpy of the previous time step. Hence, for a given pump flow rate, the RCS
pressure and the inter-nodal flow rates are obtained from Equation VId.3.7 in an
explicit manner. Subsequent to the calculation of the inter-nodal flow rates, nodal
mass derivatives are found from back substitution of flow rates into the nodal con-
servation equations of mass. Upon integration over the time step this process
yields the new nodal mass:
[]
tmmmmm
kBkxk
N
k
N
k
∆×
¦¦
−++=
+
)()()(
1
Nodal enthalpy derivatives are determined from Equation VId.3.3 by using the
calculated mass flow rates and the RCS pressure derivative as well as the updated
nodal mass. The nodal enthalpies and the RCS pressure are then determined by
explicit integration of the above quantities at the end of each time step. For exam-
ple, the nodal enthalpy becomes
thhh
k
N
k
N
k
∆×+=
+
1
and the RCS pressure
tPPP
RCS
N
RCS
N
RCS
∆×+=
+
1
. This process is continued until the specified total

3. Simplified PWR Model 795
transient time is reached. In steady state operation, where no external flow or
break flow rate exists, from Equation VId.3.1 we find:
RCPkk
mmm
==
−1
Similarly, for each node from Equation VId.3.2 we obtain the following energy
balance:
0)(
1
=−+
− kkRCPk
hhmQ
3.2. Integral Momentum Equation for a Multi-loop PWR
The primary side of a PWR may consist of two, three, four, or six loops. An inte-
gral momentum equation for loop L, for example, is obtained by integrating Equa-
tion IIIa.3.44 around the loop, which includes the reactor vessel:
()
()
³
()
[]
V,L,L,
V
V
V
L
L
.
fric
loop
fricpump
L
PPsdgP
dt
md
A
L
dt
md
A
L
∆+
¦
∆+−∆=
¦¦¸
¹
·
¨
©
§
+
¸
¹
·
¨
©
§
KK
ρ
VId.3.8
where subscripts L and V stand for Loop and vessel, respectively. We now evalu-
ate various terms in the right side of Equation VId.3.8, i.e. the friction pressure
drop, the hydrostatic pressure head, and the pump head.
3.3. Friction Pressure Drop
The vessel and the rest of the loop friction pressure drops consists of skin friction
and pressure losses at bends, the core support plate, the grid spacers, upper ple-
num, upper internals, entrance to hot leg, entrance to steam generator plenum,
tubesheet, etc. As we did in Equation VId.2.3, we also consider a two-phase fric-
tion multiplier for cases where subcooling is lost and a two-phase mixture is flow-
ing in the primary side. Calculation of the loss coefficients is discussed in Chapter
IIIb. The loss coefficients for components used exclusively in the nuclear indus-
try, such as the fuel rod grid spacers used in a specific design, are provided by the
nuclear reactor vendor. However, we may use the correlation suggested by Rust
to estimate pressure drop due to the fuel rod grid spacers as:
2
2 A
mmC
P
v
grid
ρ
ε
=∆
where
ε
is the ratio of the projected grid spacer cross section to undisturbed flow
cross section and C
v
is the drag coefficient, in turn estimated from
0245.0
91.54
−
= mC
v
.

796 VId. Applications: Simulation of Thermofluid Systems
3.4 Hydrostatic Pressure Head
The hydrostatic head in Equation VId.3.8 represents the body force due to gravity.
During normal operation when forced convection is the dominant flow regime, the
hydrostatic force is negligible compared to such pressure forces as friction pres-
sure drop and pressure rise over the pump. However, in thermal loops having
natural circulation flow regime, the hydrostatic head is the driving force. The hy-
drostatic head then becomes:
()
³
()()
[]
¦
∆=
+VL
cos.
kkk
Zgsdg
αρρ
K
K
VId.3.9
where in Equation VId.3.9 the summation is over the vessel and other regions in
the loop. These regions, as shown in Figure VId.3.2, include downcomer, lower
plenum, core, upper plenum, hot leg, steam generator, and cold leg. In this equa-
tion,
α
is the angle between the velocity vector and the vector representing the ac-
celeration of gravity. Hence, cos(
α
k
) is the same as index s introduced in Exam-
ple VId.2.1. For upward flow in the core,
α
k
=
π
and cos(
α
k
) = –1, for horizontal
flow in the hot leg,
α
k
=
π
/2 and cos(
α
k
) = 0, and for downward flow in the down-
comer,
α
k
= 0 and cos(
α
k
) = 1. In Equation VId.3.9, ∆Z
k
is the difference between
the exit and the inlet elevations to a given region hence, ∆Z
k
= Z
e
– Z
i
.
Determination of the hydrostatic head where change in the liquid is linear is
straightforward. For example in the core, Figure VId.3.3(a), assuming a near lin-
ear density profile, the hydrostatic head becomes:
()
³
()()
[]
()
core
ei
e
i
corecorecore
exitCore
inletCore
ggsdg H
2
cosH.
ρ
ρ
αρρ
+
−==
KK
Determination of the hydrostatic head in the steam generator is more involved. In
the following example we evaluate the hydrostatic head for the single-phase flow
inside the tubes of a U-tube steam generator. As shown in Figure VId.3.3(b), the
height of each leg of the average tube is l and the length of the horizontal section
is
δ
, so the average tube length becomes L = 2l +
δ
.
λ
l
s
g
δ
L = 2l +
δ
Thermal
Center
T
i
T
e
Z
core
(Z
th
)
core
Z
SG
(Z
th
)
SG
(a) (b)
Figure VId.3.3. Nodes representing (a) core and (b) tubes of a U-tube steam generator

3. Simplified PWR Model 797
Example VId.3.1. Develop the hydrostatic head for flow of water in the tubes of
a U-tube steam generator. Flow enters tubes at pressure P and temperature T
H
and
leaves at temperature T
C
. The tube average length is L.
Solution: To find the hydrostatic head in the steam generator, we find the follow-
ing:
[]
³
[]
³
[]
³
sdgssdgssdgs
L
l
H
l
H
L
H
KKKKKK
⋅−+⋅−=⋅−
+
δ
ρρρρρρ
)()()(
00
with re-
spect to Figure VId.3.3(b). Since in the upward leg cos(
π
) = –1 and in the down-
ward leg cos(0) = 1, we can write:
[]
³
[]
³
[]
³
gdssgdsssdgs
L
l
H
l
H
L
H
δ
ρρρρρρ
+
−+−−=⋅− )()()(
00
KK
We do not have the density profile to integrate. However, we have the tempera-
ture profile from Equation VIa.5.8 given as T(s) = T
sat
+ (T
H
– T
sat
)
*
/ ls
e
−
where s
is an element of length along the tube. To bridge the gap and relate the density
difference to temperature difference, we use the definition of the thermal expan-
sion coefficient of Chapter IIa,
β
=
ρρ
/])/[(
P
T∂∂− . It is assumed that
β
re-
mains constant in the temperature range of T
C
to T
H
and
β
is approximated as
β
≈
∆
ρ
/∆T)/
ρ
or ∆
ρ
=
ρβ
∆T. Thus, the integral becomes:
[]
()
(
)
³
(
)
³
{
}
³
L L
l
ls
l
ls
satHHH
dsedseTTgsdgs
0
/
0
/
**
11)(
δ
ρβρρ
+
−−
−+−−−=⋅−
KK
The integral of the argument is found as:
(
)
³
**
/*/
1
lsls
elsdse
−−
+=− , subject to
the limits 0 to l and l +
δ
to L:
[
]
()( )
{}
** *
0
*/ * * / *()/
()
() ()
L
H
ll Ll l l
HH sat
sgds
g T T l le l L le l le
δ
ρρ
βρ δ
−− +
´
¶
−⋅=
−−+ −++ −+−
KK
simplifies to:
[]
³
(
)
***
//)(/*
0
1)()(
lLllll
satHH
L
H
eeelTTgsdgs
−+−
+−−−=⋅−
δ
ρβρρ
KK
.
Substituting from Equation (2), we get:
[]
³
(
)
***
//)(/*
0
1)()(
lLllll
satHH
L
H
eeelTTgsdgs
−+−
+−−−=⋅−
δ
ρβρρ
KK
.
Replacing T
H
- T
sat
with T
H
- T
C
, yields:
[
]
()()
*** *
0
*/()// /
()
()1 /1
L
H
ll l l Ll Ll
HH C
sgds
gTTl e e e e
δ
ρρ
βρ
−+− −
´
¶
−⋅=
−−−+ −
KK
VId.3.10

798 VId. Applications: Simulation of Thermofluid Systems
Two-Phase Flow in Tubes. In Example VId.3.1, we found the hydrostatic
head for single-phase inside tubes. In the case of two-phase flow in the tubes, we
must use the mixture density as defined in Chapter V,
ρ
m
= (1 – α)
ρ
f
+
αρ
g
where
α
is given by Equation Va.1.3 as
α
= X/(aX + b). Therefore, the hydrostatic head
becomes:
()
³
()
sdg
baX
X
sdg
L
fg
f
SG
m
KKKK
..
0
µ
¶
´
¸
¸
¹
·
¨
¨
©
§
+
−
+=
ρρ
ρρ
VId.3.11
All we need to do now is to find the profile for flowing quality in the tubes. This
is accomplished by using an energy balance in an elemental length of the tube, ds
to obtain:
[
]
dsPTPTUdNdhm
ondarysatprimarysatoo
)()(
sec
−−=
π
Substituting for dh = h
fg
dX in the above equation allows us to solve for dX/ds =
[
]
fgondarysatprimarysatoo
hmPTPTUdN
/)()(
sec
−−
π
=
*
2 phase
l . We now integrate
the result, which yields X =
*
2 phase
l s + X
in
. Having the quality profile, we then
substitute into Equation VId.3.11 and integrate. The final answer depends on the
length of the boiling section (L
B
) i.e. whether L
B
< l, of l < L
B
< l +
δ
, or l +
δ
< L
B
< L. For example if L
B
< l then the hydrostatic head becomes:
()
()
()
()
»
¼
º
«
¬
ª
+
−=
µ
µ
¶
´
µ
µ
¶
´
¸
¸
¹
·
¨
¨
©
§
++
+−
+−=
b
baX
axaglds
bXsla
Xsl
gsdg
in
phase
L
L
inphase
inphasefg
fm
B
B
ln.
21
*
2
0
0
*
2
*
2
ρρ
ρρ
G
K
where a
1
=
ρ
f
– (
ρ
g
–
ρ
f
)/a and a
2
= (
ρ
g
–
ρ
f
)b/a
2
. Then from L
B
to L we use the
single-phase integral of Equation VId.3.10. The solutions for all these cases are
obtained by Kao.
Thermal Center. We now define a node property referred to as thermal cen-
ter. In lumped nodes, the thermal center may be viewed as a point at which the
heat transfer process takes place. For example, consider the node representing the
core or the steam generator U-tubes in Figure VId.3.3. Thermal center for these
nodes may be defined as:
()
[]
³
HC
L
H
TT
dsTsT
−
−
=
0
λ
VId.3.12
where
λ
is measured from the entrance to the node. For the core node, it is trivial
to show that for linear temperature rise in the core, the thermal center is located at
λ
core
= L
core
/2. Determination of the thermal center for the steam generator node,
where temperature profile is not linear, is similar to the method used in
Example VId.3.1. For U-tube steam generators it can be shown (see Problem 2)
that:
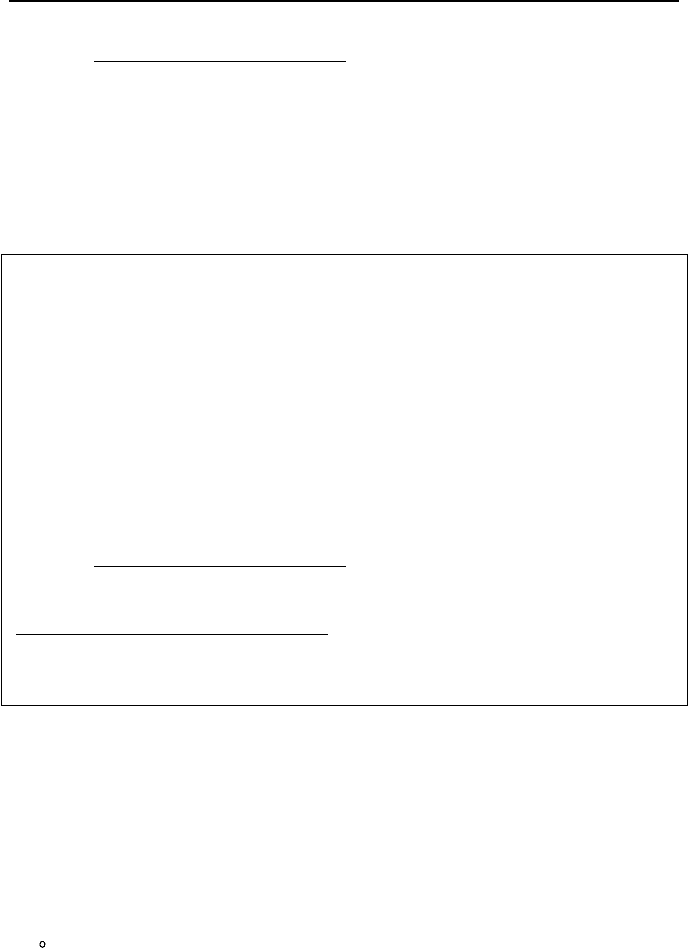
3. Simplified PWR Model 799
*
/
//)(/
*
***
1
1
l
e
eee
lL
lLllll
SG
−
−+−−
−
+−−
=
δ
λ
VId.3.13
If we now substitute
λ
SG
into Equation VId.3.10, we obtain the steam generator
hydrostatic head as:
[]
³
³
SGCHH
LL
H
TTgsdgssdgs
λρβρρρ
)()()(
00
−==⋅=⋅−
KKKK
Example VId.3.2. Find the distance to the thermal center of a steam generator
from the tube sheet. Tube-side data: =m
61E6 lbm/h, c
p
= 1.4 Btu/lbm F, N =
8485, d
o
= 0.75 in, U
o
= 1040 Btu/h ft
2
F, L = 56 ft, l = 26 ft, average length of the
U-tube horizontal section
δ
= 4 ft, cold leg temperature T
C
= 550 F, hot leg tem-
perature T
H
= 600 F.
Solution: According to Example VIa.6.2, l
*
= m
c
p
/(
π
Nd
o
U
o
). Therefore, l
*
is
found as:
l
*
= 61E6 × 1.4/[
π
× 8485 × (0.75/12) × 1040] = 49.3 ft.
We now use Equation VId.3.13:
*
/
//)(/
*
***
1
1
l
e
eee
lL
lLllll
SG
−
−+−−
−
+−−
=
δ
λ
=
3.49
1
1
3.49/56
3.49/563.49/)426(3.49/26
×
−
+−−
−
−+−−
e
eee
= 13.57 ft
This is almost equal to l/2. Indeed as l
*
ĺ,
λ
SG
= 0.5(1 +
δ
/L)l.
Having the height of the core and the steam generator thermal centers, we can
then find their corresponding elevations by adding the heights to the elevation of
the bottom of the core and the tube sheet, respectively. Hence, (Z
th
)
core
= Z
core
+
λ
core
and (Z
th
)
SG
= Z
SG
+
λ
SG
. These are shown in Figure VId.3.3.
The discussion on the hydrostatic head in a flow loop demonstrates that the hy-
drostatic head is primarily a function of the loop geometry and the working fluid
density gradient. Therefore in flow loops, the hydrostatic force is given as:
()
³
()
thHC
Loop
gsdg H.
ρρρ
−=
KK
VId.3.14
where H
th
in Equation VId.3.14 is the difference between the steam generator and
the core thermal centers given by H
th
= (Z
th
)
SG
– (Z
th
)
core
. Note that elevations of
the core and steam generator thermal centers are measured from a common refer-
ence.
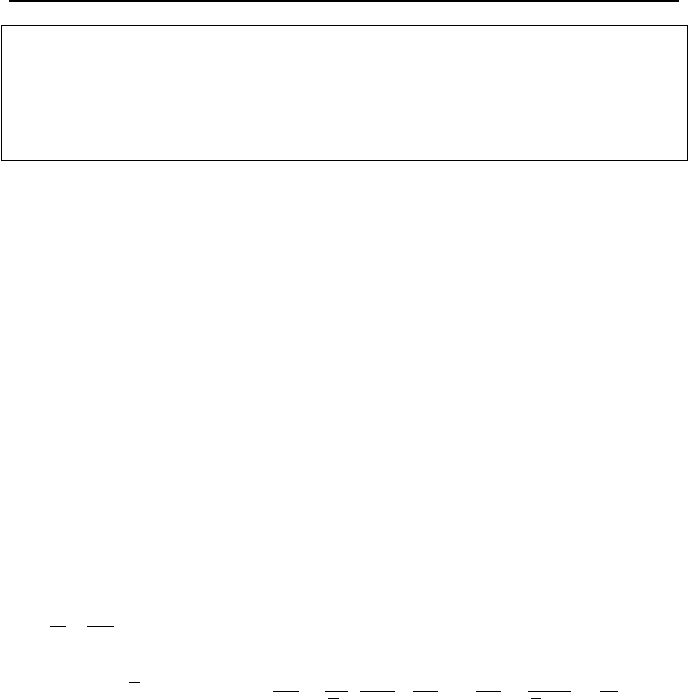
800 VId. Applications: Simulation of Thermofluid Systems
Example VId.3.3. Find the pressure difference due to the buoyancy force in a
flow loop. Data: P = 2250, T
Hot
= 600 F, T
Cold
= 550 F, Z
Heat Sink
= 61 ft, Z
Heat Source
= 31 ft. Working fluid is water.
Solution: We use Equation VId.3.14 to estimate ∆P
gravity
= (47.2 – 43.1) × (61 –
31) = 0.85 psi.
3.5. Natural Circulation in Flow Loops
Natural circulation is the preferred mode of operation when the enhancement of
the passive safety features, such as elimination of any pump failure, is a design re-
quirement. Some high rise buildings use natural circulation for the heating of their
units. This is accomplished by heating water in a boiler located in the basement
resulting in warm water flowing upward inside the riser. As water passes various
floors it deposits energy to heat the space. The colder and heavier water then
flows downward and back to the boiler, pushing the warmer water upward.
Hence, a necessary condition for establishment of natural circulation is that
H
th
> 0.
To estimate the natural circulation flow rate, we start with the single-loop of
Figure VId.3.4 and use Equation VId.2.3. Since this equation is obtained for a
single node, we integrate it over all the nodes comprising the loop. By doing so,
the static pressure difference term cancels out. Integrating Equation VId.2.3 is
equivalent to summing up all the terms of Equation IIIa.3.44 around the loop.
This results in:
()
1
22
1
22 2
11 1
1
11 1 1
K
22
n
k
k
nn n
pump k j j
k
kk k
kj j kk
k
k
Ldm
Adt
mmL
PgZZ f
DAA A
ρ
ρρ
=
+
== =
+
§·
=
¨¸
©¹
§·
§·
∆− −− − − +
¨¸
¨¸
©¹
©¹
¦
¦¦ ¦
VId.3.15
where in the case of Figure VId.3.4, n = 5. Equation VId.3.15 can be simplified
by noting that in a natural circulation loop, the pump head is zero. Note that the
pump head being zero does not necessarily mean that there is no pump in the loop.
Rather, the pump is simply not operating. A loop without a pump has by far less
frictional losses than an identical loop but equipped with a pump that is turned off.
This is because in the latter case, the working liquid must flow through the pump
volute and among the blades of the impeller. The losses due to friction in pumps
depend on the type of the pump and whether the impeller is locked or is free to
spin. For example, for the canned-motor pump of the LOFT (Reeder) experiment,
the loss coefficient for the free spinning impeller with flow in forward direction
(from pump suction to pump discharge) was estimated to be K = 3, for flow in the
reverse direction K = 12, and for flow through the pump with impeller locked
K = 20.
3. Simplified PWR Model 801
RPV
RCP
Feedwater
Steam
SG
2
3
4
1
H
th
Heat
Source
Heat Sink
Figure VId.3.4. Schematics of a single-loop PWR primary side and related data
Returning to Equation VId.3.15, we may also ignore the pressure drop term due
to the velocity change. Thus, in steady state operation, Equation VId.3.15 simpli-
fies to:
()
()
¦
−≈−−=
¦¸
¹
·
¨
©
§
+
=
+
=
n
k
thHc
k
jjk
k
n
k
kk
gZZg
D
L
f
A
m
1
1
1
2
2
HK
1
2
ρρρ
ρ
VId.3.16
The left side of Equation VId.3.16 may be shown as
ρ
2/Rm
where
2
/]K)/[(
kkkkk
ADLfR
¦
+= , known as the loop flow resistance. In the right
side of Equation VId.3.16, we made use of Equation VId.3.14 for the hydrostatic
head. If we relate the density difference (
∆
ρ
) to the corresponding temperature
difference (
∆T) by ∆
ρ
§
βρ
∆T, assuming constant
β
in the temperature range of T
C
to T
H
, Equation VId.3.16 becomes:
Tg
m
R
th
∆= H
2
1
2
βρ
ρ
VId.3.17
The change in temperature in the loop is due to the rate of heat addition in the heat
source (core) or the rate of heat rejection in the heat sink (steam generator).
Therefore, from a steady state energy balance over the heat source, for example
