Маслова Т.Н., Суходский А.М. Справочник школьника по математике. 5-11 кл
Подождите немного. Документ загружается.


ÀËÃÅÁÐÀ
Ðàçäåë I. ×ÈÑËÀ
30
3
4
/
1
4
/
ÀËÃÅÁÐÀ
§ 3. Äåéñòâèòåëüíûå ÷èñëà
31
3
4
/
1
4
/
Íàïðèìåð:
Ñðåäè äðîáåé, îáîçíà÷àþùèõ äàííîå ðàöèîíàëüíîå
÷èñëî, èìååòñÿ îäíà è òîëüêî îäíà íåñîêðàòèìàÿ äðîáü.
Äëÿ öåëûõ ÷èñåë ýòî äðîáü ñî çíàìåíàòåëåì 1.
§ 3. Äåéñòâèòåëüíûå ÷èñëà
20. Èððàöèîíàëüíûå ÷èñëà. Äëÿ èçìåðåíèÿ èñ-
ïîëüçóþòñÿ íå òîëüêî ðàöèîíàëüíûå ÷èñëà, íî è ÷èñ-
ëà èíîé ïðèðîäû, ò. å. íå ÿâëÿþùèåñÿ öåëûìè èëè
äðîáíûìè. Âñå òàêèå ÷èñëà íàçûâàþòñÿ èððàöèî-
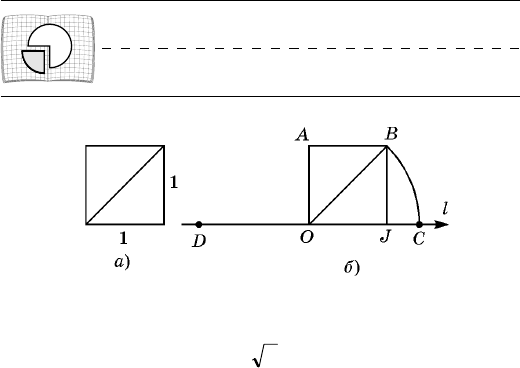
íàëüíûìè. Íàïðèìåð, äëèíà äèàãîíàëè êâàäðàòà ñî
ñòîðîíîé 1 (ðèñ. 2, à) äîëæíà âûðàæàòüñÿ íåêîòîðûì
ïîëîæèòåëüíûì ÷èñëîì r, òàêèì, ÷òî r
2
= 1
2
+
+ 1
2
(ïî òåîðåìå Ïèôàãîðà, ñì. ï. 275), ò. å. òàêèì,
÷òî r
2
= 2. ×èñëî r íå ìîæåò áûòü öåëûì, òàê êàê
1
2
= 1; 2
2
= 4; 3
2
= 9 è ò. ä. ×èñëî r íå ìîæåò áûòü è
äðîáíûì: åñëè
n
m
r =
íåñîêðàòèìàÿ äðîáü, ãäå
,1¹n
òî
2
2
2
n
m
r =
òàêæå íåñîêðàòèìàÿ äðîáü, ãäå
;1
2
¹n
çíà÷èò,
2
2
n
m
íå ÿâëÿåòñÿ öåëûì ÷èñëîì, à ïî-
òîìó íå ìîæåò áûòü ðàâíûì 2. Ïîýòîìó äëèíà äèàãî-
íàëè êâàäðàòà âûðàæàåòñÿ èððàöèîíàëüíûì ÷èñëîì,
êîòîðîå îáîçíà÷àåòñÿ
2
(÷èòàåòñÿ: «êâàäðàòíûé êî-
ðåíü èç äâóõ»). Íà ðèñ. 2, á èçîáðàæåíà êîîðäèíàò-
íàÿ ïðÿìàÿ l, OABJ êâàäðàò, OC = OB = OD. Òîãäà
êîîðäèíàòîé òî÷êè Ñ ÿâëÿåòñÿ ÷èñëî
2
, à êîîðäè-
ÿâëÿåòñÿ ÷èñëî 3, à êîîðäèíàòó òî÷êè
A
¢
çàïèñûâà-
þò 3 è ÷èòàþò: «ìèíóñ 3». Àíàëîãè÷íî, êîîðäèíàòà
òî÷êè
B
¢
, ñèììåòðè÷íîé òî÷êå  (ðèñ. 1), åñòü ÷èñëî
4,2. ×èñëà 3 è 3, 4,2 è 4,2 íàçûâàþò ïðîòèâîïî-
ëîæíûìè. ×èñëà, êîòîðûì ñîîòâåòñòâóþò òî÷êè, ðàñ-
ïîëîæåííûå íà êîîðäèíàòíîé ïðÿìîé â çàäàííîì
íàïðàâëåíèè, íàçûâàþò ïîëîæèòåëüíûìè; òàê, 1, 3,
4,2 ïîëîæèòåëüíûå ÷èñëà. ×èñëà, êîòîðûì ñîîò-
âåòñòâóþò òî÷êè, ðàñïîëîæåííûå íà êîîðäèíàòíîé
ïðÿìîé â íàïðàâëåíèè, ïðîòèâîïîëîæíîì çàäàííîìó,
íàçûâàþò îòðèöàòåëüíûìè; òàê, 3, 4,2 îòðèöà-
òåëüíûå ÷èñëà. ×èñëî 0 íå ñ÷èòàåòñÿ íè ïîëîæèòåëü-
íûì, íè îòðèöàòåëüíûì.
Çàäàííîå íàïðàâëåíèå íà êîîðäèíàòíîé ïðÿìîé
íàçûâàþò ïîëîæèòåëüíûì (îáû÷íî îíî èäåò âïðà-
âî), à íàïðàâëåíèå, ïðîòèâîïîëîæíîå çàäàííîìó,
îòðèöàòåëüíûì.
19. Ìíîæåñòâî ðàöèîíàëüíûõ ÷èñåë. Íàòóðàëü-
íûå ÷èñëà 1, 2, 3, 4, 5,... íàçûâàþò òàêæå ïîëîæèòåëü-
íûìè öåëûìè ÷èñëàìè. ×èñëà 1, 2, 3, 4, 5, ...,
ïðîòèâîïîëîæíûå íàòóðàëüíûì, íàçûâàþò îòðèöàòåëü-
íûìè öåëûìè ÷èñëàìè. ×èñëî 0 òàêæå ñ÷èòàþò öå-
ëûì ÷èñëîì. Èòàê, öåëûå ÷èñëà ýòî íàòóðàëüíûå
÷èñëà, ÷èñëà, ïðîòèâîïîëîæíûå íàòóðàëüíûì, è ÷èñ-
ëî 0.
Öåëûå ÷èñëà è äðîáè (ïîëîæèòåëüíûå è îòðèöà-
òåëüíûå) ñîñòàâëÿþò âìåñòå ìíîæåñòâî ðàöèîíàëü-
íûõ ÷èñåë.
Çàìåòèì, ÷òî ëþáîå ðàöèîíàëüíîå ÷èñëî ìîæíî
ïðåäñòàâèòü â âèäå îòíîøåíèÿ
n
m
, ãäå m öåëîå,
à n íàòóðàëüíîå ÷èñëî, ïðè÷åì îäíî è òî æå ÷èñ-
ëî ìîæíî çàïèñàòü â âèäå îòíîøåíèÿ ìíîãèìè ñïî-
ñîáàìè.
0,3 = = = .
3
10
300
1000
6
20
2 = = = ;
4
2
6
3
100
50

ÀËÃÅÁÐÀ
Ðàçäåë I. ×ÈÑËÀ
30
3
4
/
1
4
/
ÀËÃÅÁÐÀ
§ 3. Äåéñòâèòåëüíûå ÷èñëà
31
3
4
/
1
4
/
Íàïðèìåð:
Ñðåäè äðîáåé, îáîçíà÷àþùèõ äàííîå ðàöèîíàëüíîå
÷èñëî, èìååòñÿ îäíà è òîëüêî îäíà íåñîêðàòèìàÿ äðîáü.
Äëÿ öåëûõ ÷èñåë ýòî äðîáü ñî çíàìåíàòåëåì 1.
§ 3. Äåéñòâèòåëüíûå ÷èñëà
20. Èððàöèîíàëüíûå ÷èñëà. Äëÿ èçìåðåíèÿ èñ-
ïîëüçóþòñÿ íå òîëüêî ðàöèîíàëüíûå ÷èñëà, íî è ÷èñ-
ëà èíîé ïðèðîäû, ò. å. íå ÿâëÿþùèåñÿ öåëûìè èëè
äðîáíûìè. Âñå òàêèå ÷èñëà íàçûâàþòñÿ èððàöèî-
íàëüíûìè. Íàïðèìåð, äëèíà äèàãîíàëè êâàäðàòà ñî
ñòîðîíîé 1 (ðèñ. 2, à) äîëæíà âûðàæàòüñÿ íåêîòîðûì
ïîëîæèòåëüíûì ÷èñëîì r, òàêèì, ÷òî r
2
= 1
2
+
+ 1
2
(ïî òåîðåìå Ïèôàãîðà, ñì. ï. 275), ò. å. òàêèì,
÷òî r
2
= 2. ×èñëî r íå ìîæåò áûòü öåëûì, òàê êàê
1
2
= 1; 2
2
= 4; 3
2
= 9 è ò. ä. ×èñëî r íå ìîæåò áûòü è
äðîáíûì: åñëè
n
m
r =
íåñîêðàòèìàÿ äðîáü, ãäå
,1¹n
òî
2
2
2
n
m
r =
òàêæå íåñîêðàòèìàÿ äðîáü, ãäå
;1
2
¹n
çíà÷èò,
2
2
n
m
íå ÿâëÿåòñÿ öåëûì ÷èñëîì, à ïî-
òîìó íå ìîæåò áûòü ðàâíûì 2. Ïîýòîìó äëèíà äèàãî-
íàëè êâàäðàòà âûðàæàåòñÿ èððàöèîíàëüíûì ÷èñëîì,
êîòîðîå îáîçíà÷àåòñÿ
2
(÷èòàåòñÿ: «êâàäðàòíûé êî-
ðåíü èç äâóõ»). Íà ðèñ. 2, á èçîáðàæåíà êîîðäèíàò-
íàÿ ïðÿìàÿ l, OABJ êâàäðàò, OC = OB = OD. Òîãäà
êîîðäèíàòîé òî÷êè Ñ ÿâëÿåòñÿ ÷èñëî
2
, à êîîðäè-
ÿâëÿåòñÿ ÷èñëî 3, à êîîðäèíàòó òî÷êè
A
¢
çàïèñûâà-
þò 3 è ÷èòàþò: «ìèíóñ 3». Àíàëîãè÷íî, êîîðäèíàòà
òî÷êè
B
¢
, ñèììåòðè÷íîé òî÷êå  (ðèñ. 1), åñòü ÷èñëî
4,2. ×èñëà 3 è 3, 4,2 è 4,2 íàçûâàþò ïðîòèâîïî-
ëîæíûìè. ×èñëà, êîòîðûì ñîîòâåòñòâóþò òî÷êè, ðàñ-
ïîëîæåííûå íà êîîðäèíàòíîé ïðÿìîé â çàäàííîì
íàïðàâëåíèè, íàçûâàþò ïîëîæèòåëüíûìè; òàê, 1, 3,
4,2 ïîëîæèòåëüíûå ÷èñëà. ×èñëà, êîòîðûì ñîîò-
âåòñòâóþò òî÷êè, ðàñïîëîæåííûå íà êîîðäèíàòíîé
ïðÿìîé â íàïðàâëåíèè, ïðîòèâîïîëîæíîì çàäàííîìó,
íàçûâàþò îòðèöàòåëüíûìè; òàê, 3, 4,2 îòðèöà-
òåëüíûå ÷èñëà. ×èñëî 0 íå ñ÷èòàåòñÿ íè ïîëîæèòåëü-
íûì, íè îòðèöàòåëüíûì.
Çàäàííîå íàïðàâëåíèå íà êîîðäèíàòíîé ïðÿìîé
íàçûâàþò ïîëîæèòåëüíûì (îáû÷íî îíî èäåò âïðà-
âî), à íàïðàâëåíèå, ïðîòèâîïîëîæíîå çàäàííîìó,
îòðèöàòåëüíûì.
19. Ìíîæåñòâî ðàöèîíàëüíûõ ÷èñåë. Íàòóðàëü-
íûå ÷èñëà 1, 2, 3, 4, 5,... íàçûâàþò òàêæå ïîëîæèòåëü-
íûìè öåëûìè ÷èñëàìè. ×èñëà 1, 2, 3, 4, 5, ...,
ïðîòèâîïîëîæíûå íàòóðàëüíûì, íàçûâàþò îòðèöàòåëü-
íûìè öåëûìè ÷èñëàìè. ×èñëî 0 òàêæå ñ÷èòàþò öå-
ëûì ÷èñëîì. Èòàê, öåëûå ÷èñëà ýòî íàòóðàëüíûå
÷èñëà, ÷èñëà, ïðîòèâîïîëîæíûå íàòóðàëüíûì, è ÷èñ-
ëî 0.
Öåëûå ÷èñëà è äðîáè (ïîëîæèòåëüíûå è îòðèöà-
òåëüíûå) ñîñòàâëÿþò âìåñòå ìíîæåñòâî ðàöèîíàëü-
íûõ ÷èñåë.
Çàìåòèì, ÷òî ëþáîå ðàöèîíàëüíîå ÷èñëî ìîæíî
ïðåäñòàâèòü â âèäå îòíîøåíèÿ
n
m
, ãäå m öåëîå,
à n íàòóðàëüíîå ÷èñëî, ïðè÷åì îäíî è òî æå ÷èñ-
ëî ìîæíî çàïèñàòü â âèäå îòíîøåíèÿ ìíîãèìè ñïî-
ñîáàìè.
0,3 = = = .
3
10
300
1000
6
20
2 = = = ;
4
2
6
3
100
50
ÀËÃÅÁÐÀ
§ 3. Äåéñòâèòåëüíûå ÷èñëà
ÀËÃÅÁÐÀ
Ðàçäåë I. ×ÈÑËÀ
33
32
3
4
/
1
4
/
3
4
/
1
4
/
22. ×èñëîâàÿ ïëîñêîñòü. Ïðÿìîóãîëüíàÿ äåêàð-
òîâà ñèñòåìà êîîðäèíàò íà ïëîñêîñòè è â ïðîñòðàí-
ñòâå. Ïîä ïàðîé ÷èñåë îáû÷íî ïîíèìàþò äâà ÷èñëà,
êîòîðûå ðàññìàòðèâàþòñÿ â îïðåäåëåííîì ïîðÿäêå
(óïîðÿäî÷åííàÿ ïàðà). Ìíîæåñòâî âñåõ ïàð äåéñòâè-
òåëüíûõ ÷èñåë íàçûâàþò ÷èñëîâîé ïëîñêîñòüþ.
Êàê äëÿ ìíîæåñòâà âñåõ äåéñòâèòåëüíûõ ÷èñåë (èëè
÷èñëîâîé ïðÿìîé) åñòü ãåîìåòðè÷åñêàÿ ìîäåëü
êîîðäèíàòíàÿ ïðÿìàÿ (ñì. ïï. 18 è 21), òàê è äëÿ
ìíîæåñòâà âñåõ ïàð äåéñòâèòåëüíûõ ÷èñåë (÷èñëî-
âîé ïëîñêîñòè) åñòü ãåîìåòðè÷åñêàÿ ìîäåëü êîîð-
äèíàòíàÿ ïëîñêîñòü. Êîîðäèíàòíàÿ ïëîñêîñòü
õOy îïðåäåëÿåòñÿ äâóìÿ âçàèìíî ïåðïåíäèêóëÿð-
íûìè ïðÿìûìè ñ îáùèì íà÷àëîì Î è îäèíàêîâûì
ìàñøòàáîì (ðèñ. 3). Òî÷êà Î íàçûâàåòñÿ íà÷àëîì
êîîðäèíàò. Ãîðèçîíòàëüíàÿ ïðÿìàÿ íàçûâàåòñÿ
îñüþ àáñöèññ èëè îñüþ Îõ, âåðòèêàëüíàÿ îñüþ
îðäèíàò èëè îñüþ Îy. Ãîâîðÿò, ÷òî ýòè îñè îáðàçó-
þò ïðÿìîóãîëüíóþ äåêàðòîâó ñèñòåìó êîîðäè-
íàò íà ïëîñêîñòè.
Êàæäîé òî÷êå ïëîñêîñòè xOy ñîîòâåòñòâóåò ïàðà
÷èñåë êîîðäèíàò ýòîé òî÷êè îòíîñèòåëüíî äàííîé
êîîîðäèíàòíîé ñèñòåìû. Ðàññìîòðèì ïðÿìîóãîëüíûå
ïðîåêöèè òî÷êè Ì íà îñè Îõ è Oy (ðèñ. 3); ñîîòâåò-
íàòîé òî÷êè D ÷èñëî
2
. Îáå òî÷êè C è D èìåþò
èððàöèîíàëüíûå êîîðäèíàòû.
Òàê êàê ëþáîå ðàöèîíàëüíîå ÷èñëî ìîæíî çàïè-
ñàòü â âèäå áåñêîíå÷íîé äåñÿòè÷íîé äðîáè (ñì. ï. 16)
è â ñâîþ î÷åðåäü ëþáàÿ áåñêîíå÷íàÿ äåñÿòè÷íàÿ ïå-
ðèîäè÷åñêàÿ äðîáü ïðåäñòàâëÿåò ñîáîé ðàöèîíàëüíîå
÷èñëî (ñì. ï. 17), òî êàæäîå èððàöèîíàëüíîå ÷èñëî
ìîæíî çàïèñàòü â âèäå áåñêîíå÷íîé äåñÿòè÷íîé
äðîáè è â ñâîþ î÷åðåäü ëþáàÿ áåñêîíå÷íàÿ äåñÿòè÷-
íàÿ íåïåðèîäè÷åñêàÿ äðîáü åñòü èððàöèîíàëüíîå
÷èñëî.
21. Ìíîæåñòâî äåéñòâèòåëüíûõ ÷èñåë. ×èñëîâàÿ
ïðÿìàÿ. Ðàöèîíàëüíûå è èððàöèîíàëüíûå ÷èñëà ñî-
ñòàâëÿþò âìåñòå ìíîæåñòâî äåéñòâèòåëüíûõ ÷è-
ñåë. Êàæäîìó äåéñòâèòåëüíîìó ÷èñëó ñîîòâåòñòâóåò
åäèíñòâåííàÿ òî÷êà êîîðäèíàòíîé ïðÿìîé. Êàæäàÿ
òî÷êà êîîðäèíàòíîé ïðÿìîé ñîîòâåòñòâóåò åäèíñòâåí-
íîìó äåéñòâèòåëüíîìó ÷èñëó (äîñòàòî÷íî íàéòè ðàñ-
ñòîÿíèå äî ýòîé òî÷êè îò íà÷àëà îòñ÷åòà è ïîñòàâèòü
ïåðåä íàéäåííûì ÷èñëîì çíàê «+» èëè «» â çàâè-
ñèìîñòè îò òîãî, ñïðàâà èëè ñëåâà îò íà÷àëà îòñ÷åòà
íàõîäèòñÿ çàäàííàÿ òî÷êà).
Ìíîæåñòâî äåéñòâèòåëüíûõ ÷èñåë íàçûâàþò òàê-
æå ÷èñëîâîé ïðÿìîé. Ãåîìåòðè÷åñêîé ìîäåëüþ ÷èñ-
ëîâîé ïðÿìîé ñëóæèò êîîðäèíàòíàÿ ïðÿìàÿ.
Ðèñ. 3
Ðèñ. 2

ÀËÃÅÁÐÀ
§ 3. Äåéñòâèòåëüíûå ÷èñëà
ÀËÃÅÁÐÀ
Ðàçäåë I. ×ÈÑËÀ
33
32
3
4
/
1
4
/
3
4
/
1
4
/
22. ×èñëîâàÿ ïëîñêîñòü. Ïðÿìîóãîëüíàÿ äåêàð-
òîâà ñèñòåìà êîîðäèíàò íà ïëîñêîñòè è â ïðîñòðàí-
ñòâå. Ïîä ïàðîé ÷èñåë îáû÷íî ïîíèìàþò äâà ÷èñëà,
êîòîðûå ðàññìàòðèâàþòñÿ â îïðåäåëåííîì ïîðÿäêå
(óïîðÿäî÷åííàÿ ïàðà). Ìíîæåñòâî âñåõ ïàð äåéñòâè-
òåëüíûõ ÷èñåë íàçûâàþò ÷èñëîâîé ïëîñêîñòüþ.
Êàê äëÿ ìíîæåñòâà âñåõ äåéñòâèòåëüíûõ ÷èñåë (èëè
÷èñëîâîé ïðÿìîé) åñòü ãåîìåòðè÷åñêàÿ ìîäåëü
êîîðäèíàòíàÿ ïðÿìàÿ (ñì. ïï. 18 è 21), òàê è äëÿ
ìíîæåñòâà âñåõ ïàð äåéñòâèòåëüíûõ ÷èñåë (÷èñëî-
âîé ïëîñêîñòè) åñòü ãåîìåòðè÷åñêàÿ ìîäåëü êîîð-
äèíàòíàÿ ïëîñêîñòü. Êîîðäèíàòíàÿ ïëîñêîñòü
õOy îïðåäåëÿåòñÿ äâóìÿ âçàèìíî ïåðïåíäèêóëÿð-
íûìè ïðÿìûìè ñ îáùèì íà÷àëîì Î è îäèíàêîâûì
ìàñøòàáîì (ðèñ. 3). Òî÷êà Î íàçûâàåòñÿ íà÷àëîì
êîîðäèíàò. Ãîðèçîíòàëüíàÿ ïðÿìàÿ íàçûâàåòñÿ
îñüþ àáñöèññ èëè îñüþ Îõ, âåðòèêàëüíàÿ îñüþ
îðäèíàò èëè îñüþ Îy. Ãîâîðÿò, ÷òî ýòè îñè îáðàçó-
þò ïðÿìîóãîëüíóþ äåêàðòîâó ñèñòåìó êîîðäè-
íàò íà ïëîñêîñòè.
Êàæäîé òî÷êå ïëîñêîñòè xOy ñîîòâåòñòâóåò ïàðà
÷èñåë êîîðäèíàò ýòîé òî÷êè îòíîñèòåëüíî äàííîé
êîîîðäèíàòíîé ñèñòåìû. Ðàññìîòðèì ïðÿìîóãîëüíûå
ïðîåêöèè òî÷êè Ì íà îñè Îõ è Oy (ðèñ. 3); ñîîòâåò-
íàòîé òî÷êè D ÷èñëî
2
. Îáå òî÷êè C è D èìåþò
èððàöèîíàëüíûå êîîðäèíàòû.
Òàê êàê ëþáîå ðàöèîíàëüíîå ÷èñëî ìîæíî çàïè-
ñàòü â âèäå áåñêîíå÷íîé äåñÿòè÷íîé äðîáè (ñì. ï. 16)
è â ñâîþ î÷åðåäü ëþáàÿ áåñêîíå÷íàÿ äåñÿòè÷íàÿ ïå-
ðèîäè÷åñêàÿ äðîáü ïðåäñòàâëÿåò ñîáîé ðàöèîíàëüíîå
÷èñëî (ñì. ï. 17), òî êàæäîå èððàöèîíàëüíîå ÷èñëî
ìîæíî çàïèñàòü â âèäå áåñêîíå÷íîé äåñÿòè÷íîé
äðîáè è â ñâîþ î÷åðåäü ëþáàÿ áåñêîíå÷íàÿ äåñÿòè÷-
íàÿ íåïåðèîäè÷åñêàÿ äðîáü åñòü èððàöèîíàëüíîå
÷èñëî.
21. Ìíîæåñòâî äåéñòâèòåëüíûõ ÷èñåë. ×èñëîâàÿ
ïðÿìàÿ. Ðàöèîíàëüíûå è èððàöèîíàëüíûå ÷èñëà ñî-
ñòàâëÿþò âìåñòå ìíîæåñòâî äåéñòâèòåëüíûõ ÷è-
ñåë. Êàæäîìó äåéñòâèòåëüíîìó ÷èñëó ñîîòâåòñòâóåò
åäèíñòâåííàÿ òî÷êà êîîðäèíàòíîé ïðÿìîé. Êàæäàÿ
òî÷êà êîîðäèíàòíîé ïðÿìîé ñîîòâåòñòâóåò åäèíñòâåí-
íîìó äåéñòâèòåëüíîìó ÷èñëó (äîñòàòî÷íî íàéòè ðàñ-
ñòîÿíèå äî ýòîé òî÷êè îò íà÷àëà îòñ÷åòà è ïîñòàâèòü
ïåðåä íàéäåííûì ÷èñëîì çíàê «+» èëè «» â çàâè-
ñèìîñòè îò òîãî, ñïðàâà èëè ñëåâà îò íà÷àëà îòñ÷åòà
íàõîäèòñÿ çàäàííàÿ òî÷êà).
Ìíîæåñòâî äåéñòâèòåëüíûõ ÷èñåë íàçûâàþò òàê-
æå ÷èñëîâîé ïðÿìîé. Ãåîìåòðè÷åñêîé ìîäåëüþ ÷èñ-
ëîâîé ïðÿìîé ñëóæèò êîîðäèíàòíàÿ ïðÿìàÿ.
Ðèñ. 3
Ðèñ. 2
ÀËÃÅÁÐÀ
§ 3. Äåéñòâèòåëüíûå ÷èñëà
ÀËÃÅÁÐÀ
Ðàçäåë I. ×ÈÑËÀ
35
34
3
4
/
1
4
/
3
4
/
1
4
/
Òî÷êó Ì ñ êîîðäèíàòàìè x, y, z áóäåì çàïèñûâàòü
òàê: Ì (x; y; z), ïðè÷åì õ íàçûâàåòñÿ àáñöèññîé, y
îðäèíàòîé, à z àïïëèêàòîé.
Èòàê, êàæäîé òî÷êå Ì â ïðîñòðàíñòâå ñîîòâåòñò-
âóþò òðè ÷èñëà, âçÿòûå â îïðåäåëåííîì ïîðÿäêå,
êîîðäèíàòû òî÷êè Ì â ïðîñòðàíñòâå.
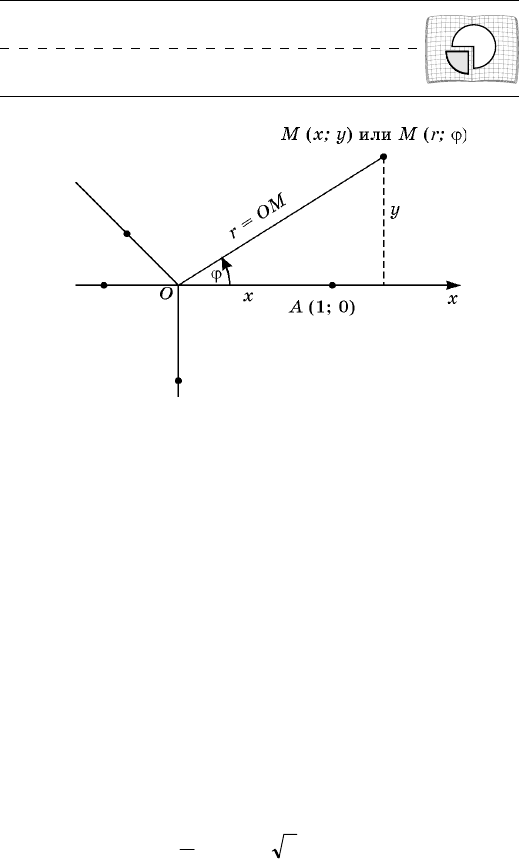
23. Ïîëÿðíàÿ ñèñòåìà êîîðäèíàò. Ïîëîæåíèå òî÷-
êè íà ïëîñêîñòè ìîæíî çàäàòü íå òîëüêî åå äåêàðòî-
âûìè ïðÿìîóãîëüíûìè êîîðäèíàòàìè õ, y, íî è äðóãè-
ìè ñïîñîáàìè. Ñîåäèíèì, íàïðèìåð, òî÷êó Ì ñ íà÷à-
ëîì Î (ðèñ. 5) è ðàññìîòðèì ñëåäóþùèå äâà ÷èñëà:
äëèíó îòðåçêà ÎÌ = r è óãîë j íàêëîíà ýòîãî îòðåçêà
ê ïîëîæèòåëüíîìó íàïðàâëåíèþ îñè Îõ (ýòîò óãîë
ñ÷èòàåòñÿ ïîëîæèòåëüíûì, åñëè ïîâîðîò îò îñè Îõ äî
åå ñîâìåùåíèÿ ñ íàïðàâëåíèåì ÎÌ ïðîèñõîäèò ïðî-
òèâ ÷àñîâîé ñòðåëêè, è îòðèöàòåëüíûì â ïðîòèâíîì
ñëó÷àå). Îòðåçîê r = ÎÌ íàçûâàåòñÿ ïîëÿðíûì ðà-
äèóñîì òî÷êè Ì, óãîë j åå ïîëÿðíûì óãëîì, ïàðà
÷èñåë (r; j) åå ïîëÿðíûìè êîîðäèíàòàìè, òî÷êà
Î ïîëþñîì, îñü Ox ïîëÿðíîé îñüþ. Òàêàÿ ñèñ-
òåìà êîîðäèíàò íàçûâàåòñÿ ïîëÿðíîé.
ñòâóþùèå òî÷êè íà îñÿõ Îõ è Oy îáîçíà÷å-
íû ÷åðåç Ì
õ
è Ì
y
.Òî÷êà Ì
õ
èìååò êîîðäèíàòó
(àáñöèññó) õ, òî÷êà Ì
y
êîîðäèíàòó (îðäèíàòó)
y. Ýòè äâà ÷èñëà, çàïèñàííûå â óêàçàííîì ïîðÿä-
êå, íàçûâàþò êîîðäèíàòàìè òî÷êè Ì è ïèøóò
Ì (õ; y).
Îñè êîîðäèíàò äåëÿò êîîðäèíàòíóþ ïëîñêîñòü íà
÷åòûðå êîîðäèíàòíûå ÷åòâåðòè (êâàäðàíòû), êî-
òîðûå íóìåðóþòñÿ ðèìñêèìè öèôðàìè (ñì. ðèñ. 3).
Çíàêè êîîðäèíàò òî÷êè â çàâèñèìîñòè îò òîãî, â êà-
êîì êâàäðàíòå îíà ëåæèò, óêàçàíû íà ðèñ. 3.
Òî÷êè, ëåæàùèå íà îñè Îõ, èìåþò îðäèíàòó y, ðàâ-
íóþ íóëþ; òî÷êè íà îñè Îy àáñöèññó õ, ðàâíóþ
íóëþ.
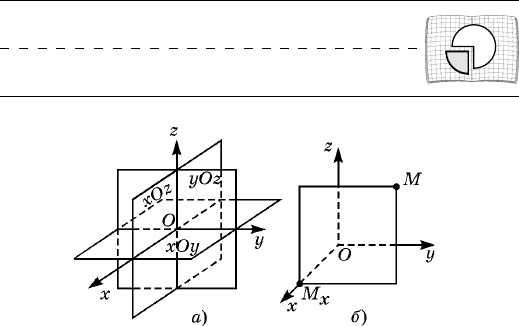
Àíàëîãè÷íî ââîäèòñÿ ïðÿìîóãîëüíàÿ äåêàðòî-
âà ñèñòåìà êîîðäèíàò â ïðîñòðàíñòâå. Äëÿ ýòî-
ãî âîçüìåì òðè ïîïàðíî ïåðïåíäèêóëÿðíûå ïðÿìûå
ñ îáùèì íà÷àëîì Î è îäèíàêîâûì ìàñøòàáîì (ðèñ.
4, à). Ïðîâåäåì ÷åðåç êàæäóþ ïàðó ýòèõ ïðÿìûõ
ïëîñêîñòü. Ïëîñêîñòü, ïðîõîäÿùàÿ ÷åðåç ïðÿìûå Îõ
è Îy, íàçûâàåòñÿ ïëîñêîñòüþ õÎy, à äâå äðóãèå
ïëîñêîñòÿìè õÎz è yÎz. Òî÷êà Î íàçûâàåòñÿ íà÷à-
ëîì êîîðäèíàò, ïðÿìûå Îõ, Îy, è Îz êîîðäèíàò-
íûìè îñÿìè, à ïëîñêîñòè õÎó, õÎz è óÎz êîîðäè-
íàòíûìè ïëîñêîñòÿìè. Ïðè ýòîì îñü Îõ íàçûâà-
åòñÿ îñüþ àáñöèññ, îñü Îy îñüþ îðäèíàò, à îñü Îz
îñüþ àïïëèêàò.
Âîçüìåì ïðîèçâîëüíóþ òî÷êó Ì è ïðîâåäåì ÷å-
ðåç íåå ïëîñêîñòü, ïàðàëëåëüíóþ ïëîñêîñòè yOz
(ðèñ. 4, á); òîãäà ïîñòðîåííàÿ ïëîñêîñòü ïåðåñå÷åò îñü
Îõ â òî÷êå Ì
õ
.
Êîîðäèíàòîé õ òî÷êè Ì ÿâëÿåòñÿ ÷èñëî, ðàâíîå ïî
ìîäóëþ äëèíå îòðåçêà ÎÌ
õ
(îíî ïîëîæèòåëüíî, åñëè
Ì
õ
ëåæèò íà ïîëîæèòåëüíîé ïîëóîñè, è îòðèöàòåëü-
íî, åñëè Ì
õ
ëåæèò íà îòðèöàòåëüíîé ïîëóîñè). Àíà-
ëîãè÷íî îïðåäåëÿþòñÿ êîîðäèíàòû y è z òî÷êè Ì.
Ðèñ. 4
ÀËÃÅÁÐÀ
§ 3. Äåéñòâèòåëüíûå ÷èñëà
ÀËÃÅÁÐÀ
Ðàçäåë I. ×ÈÑËÀ
35
34
3
4
/
1
4
/
3
4
/
1
4
/
Òî÷êó Ì ñ êîîðäèíàòàìè x, y, z áóäåì çàïèñûâàòü
òàê: Ì (x; y; z), ïðè÷åì õ íàçûâàåòñÿ àáñöèññîé, y
îðäèíàòîé, à z àïïëèêàòîé.
Èòàê, êàæäîé òî÷êå Ì â ïðîñòðàíñòâå ñîîòâåòñò-
âóþò òðè ÷èñëà, âçÿòûå â îïðåäåëåííîì ïîðÿäêå,
êîîðäèíàòû òî÷êè Ì â ïðîñòðàíñòâå.
23. Ïîëÿðíàÿ ñèñòåìà êîîðäèíàò. Ïîëîæåíèå òî÷-
êè íà ïëîñêîñòè ìîæíî çàäàòü íå òîëüêî åå äåêàðòî-
âûìè ïðÿìîóãîëüíûìè êîîðäèíàòàìè õ, y, íî è äðóãè-
ìè ñïîñîáàìè. Ñîåäèíèì, íàïðèìåð, òî÷êó Ì ñ íà÷à-
ëîì Î (ðèñ. 5) è ðàññìîòðèì ñëåäóþùèå äâà ÷èñëà:
äëèíó îòðåçêà ÎÌ = r è óãîë j íàêëîíà ýòîãî îòðåçêà
ê ïîëîæèòåëüíîìó íàïðàâëåíèþ îñè Îõ (ýòîò óãîë
ñ÷èòàåòñÿ ïîëîæèòåëüíûì, åñëè ïîâîðîò îò îñè Îõ äî
åå ñîâìåùåíèÿ ñ íàïðàâëåíèåì ÎÌ ïðîèñõîäèò ïðî-
òèâ ÷àñîâîé ñòðåëêè, è îòðèöàòåëüíûì â ïðîòèâíîì
ñëó÷àå). Îòðåçîê r = ÎÌ íàçûâàåòñÿ ïîëÿðíûì ðà-
äèóñîì òî÷êè Ì, óãîë j åå ïîëÿðíûì óãëîì, ïàðà
÷èñåë (r; j) åå ïîëÿðíûìè êîîðäèíàòàìè, òî÷êà
Î ïîëþñîì, îñü Ox ïîëÿðíîé îñüþ. Òàêàÿ ñèñ-
òåìà êîîðäèíàò íàçûâàåòñÿ ïîëÿðíîé.
ñòâóþùèå òî÷êè íà îñÿõ Îõ è Oy îáîçíà÷å-
íû ÷åðåç Ì
õ
è Ì
y
.Òî÷êà Ì
õ
èìååò êîîðäèíàòó
(àáñöèññó) õ, òî÷êà Ì
y
êîîðäèíàòó (îðäèíàòó)
y. Ýòè äâà ÷èñëà, çàïèñàííûå â óêàçàííîì ïîðÿä-
êå, íàçûâàþò êîîðäèíàòàìè òî÷êè Ì è ïèøóò
Ì (õ; y).
Îñè êîîðäèíàò äåëÿò êîîðäèíàòíóþ ïëîñêîñòü íà
÷åòûðå êîîðäèíàòíûå ÷åòâåðòè (êâàäðàíòû), êî-
òîðûå íóìåðóþòñÿ ðèìñêèìè öèôðàìè (ñì. ðèñ. 3).
Çíàêè êîîðäèíàò òî÷êè â çàâèñèìîñòè îò òîãî, â êà-
êîì êâàäðàíòå îíà ëåæèò, óêàçàíû íà ðèñ. 3.
Òî÷êè, ëåæàùèå íà îñè Îõ, èìåþò îðäèíàòó y, ðàâ-
íóþ íóëþ; òî÷êè íà îñè Îy àáñöèññó õ, ðàâíóþ
íóëþ.
Àíàëîãè÷íî ââîäèòñÿ ïðÿìîóãîëüíàÿ äåêàðòî-
âà ñèñòåìà êîîðäèíàò â ïðîñòðàíñòâå. Äëÿ ýòî-
ãî âîçüìåì òðè ïîïàðíî ïåðïåíäèêóëÿðíûå ïðÿìûå
ñ îáùèì íà÷àëîì Î è îäèíàêîâûì ìàñøòàáîì (ðèñ.
4, à). Ïðîâåäåì ÷åðåç êàæäóþ ïàðó ýòèõ ïðÿìûõ
ïëîñêîñòü. Ïëîñêîñòü, ïðîõîäÿùàÿ ÷åðåç ïðÿìûå Îõ
è Îy, íàçûâàåòñÿ ïëîñêîñòüþ õÎy, à äâå äðóãèå
ïëîñêîñòÿìè õÎz è yÎz. Òî÷êà Î íàçûâàåòñÿ íà÷à-
ëîì êîîðäèíàò, ïðÿìûå Îõ, Îy, è Îz êîîðäèíàò-
íûìè îñÿìè, à ïëîñêîñòè õÎó, õÎz è óÎz êîîðäè-
íàòíûìè ïëîñêîñòÿìè. Ïðè ýòîì îñü Îõ íàçûâà-
åòñÿ îñüþ àáñöèññ, îñü Îy îñüþ îðäèíàò, à îñü Îz
îñüþ àïïëèêàò.
Âîçüìåì ïðîèçâîëüíóþ òî÷êó Ì è ïðîâåäåì ÷å-
ðåç íåå ïëîñêîñòü, ïàðàëëåëüíóþ ïëîñêîñòè yOz
(ðèñ. 4, á); òîãäà ïîñòðîåííàÿ ïëîñêîñòü ïåðåñå÷åò îñü
Îõ â òî÷êå Ì
õ
.
Êîîðäèíàòîé õ òî÷êè Ì ÿâëÿåòñÿ ÷èñëî, ðàâíîå ïî
ìîäóëþ äëèíå îòðåçêà ÎÌ
õ
(îíî ïîëîæèòåëüíî, åñëè
Ì
õ
ëåæèò íà ïîëîæèòåëüíîé ïîëóîñè, è îòðèöàòåëü-
íî, åñëè Ì
õ
ëåæèò íà îòðèöàòåëüíîé ïîëóîñè). Àíà-
ëîãè÷íî îïðåäåëÿþòñÿ êîîðäèíàòû y è z òî÷êè Ì.
Ðèñ. 4
ÀËÃÅÁÐÀ
§ 3. Äåéñòâèòåëüíûå ÷èñëà
ÀËÃÅÁÐÀ
Ðàçäåë I. ×ÈÑËÀ
37
36
3
4
/
1
4
/
3
4
/
1
4
/
24. Îáîçíà÷åíèÿ íåêîòîðûõ ÷èñëîâûõ ìíîæåñòâ.
Îñíîâíûå ïîíÿòèÿ, ñâÿçàííûå ñ ìíîæåñòâàìè. Ïðè-
âåäåì îáîçíà÷åíèÿ ÷àñòî âñòðå÷àþùèõñÿ ÷èñëîâûõ
ìíîæåñòâ:
N ìíîæåñòâî íàòóðàëüíûõ ÷èñåë;
Z ìíîæåñòâî öåëûõ ÷èñåë;
Q ìíîæåñòâî ðàöèîíàëüíûõ ÷èñåë;
I ìíîæåñòâî èððàöèîíàëüíûõ ÷èñåë;
R ìíîæåñòâî äåéñòâèòåëüíûõ ÷èñåë;
Ñ ìíîæåñòâî êîìïëåêñíûõ ÷èñåë (ñì. ï. 45).
Åñëè à ÿâëÿåòñÿ ýëåìåíòîì ìíîæåñòâà À, òî ãîâî-
ðÿò, ÷òî à ïðèíàäëåæèò ìíîæåñòâó À è ïèøóò
Aa Î
(Î çíàê ïðèíàäëåæíîñòè).  ïðîòèâíîì ñëó÷àå,
ò. å. åñëè à íå ÿâëÿåòñÿ ýëåìåíòîì ìíîæåñòâà À,
ïèøóò
Aa Ï
. Òàê, íàïðèìåð,
NÎ5
, à
;NÏO
,5 ZÎ-
à
;4,1 ZÏ ,
3
2
QÎ
à
.2 QÏ
Íà ðèñ. 5 èçîáðàæåíû òî÷êè, çàäàííûå ïîëÿðíûìè
êîîðäèíàòàìè: À (1; 0),
,
2
;
5
3
÷
ø
ö
ç
è
æ
p
-B
.
4
3
;
2
1
÷
ø
ö
ç
è
æ
p
C
÷
ø
ö
ç
è
æ
p;
5
3
D
.
Çíàÿ ïîëÿðíûå êîîðäèíàòû òî÷êè, ìîæíî íàéòè
åå äåêàðòîâû êîîðäèíàòû ïî ôîðìóëàì
,sin,cos j=j= ryrx
(1)
íåïîñðåäñòâåííî âûòåêàþùèì èç îïðåäåëåíèÿ òðè-
ãîíîìåòðè÷åñêèõ ôóíêöèé (ñì. ï. 118). Íàîáîðîò, åñëè
èçâåñòíû äåêàðòîâû êîîðäèíàòû òî÷êè, òî åå ïîëÿð-
íûå êîîðäèíàòû íàõîäÿòñÿ ïî ôîðìóëàì
,
22
yxr +=
,
.sin
22
yx
y
r
y
+
-=
j
(2)
Ï ð è ì å ð. Íàéòè ïîëÿðíûå êîîðäèíàòû òî÷êè Ì
(4;
34
).
q Èñïîëüçóÿ ïåðâóþ èç ôîðìóë (2), íàõîäèì
.84816)34()4(
22
=+=+-=r Äàëåå, ñîãëàñíî
âòîðîé è òðåòüåé ôîðìóëàì (2), èìååì
,
2
1
8
4
cos =
-
=
j
,
2
3
8
34
sin ==j
îòêóäà ñëåäóåò, ÷òî
.
3
2p
=j
Èòàê,
.
3
2
;8
÷
ø
ö
ç
è
æ
p
M
n
0
,
Ðèñ. 5
cos j =
x
r
x
Ö
x
2
+ y
2
ÀËÃÅÁÐÀ
§ 3. Äåéñòâèòåëüíûå ÷èñëà
ÀËÃÅÁÐÀ
Ðàçäåë I. ×ÈÑËÀ
37
36
3
4
/
1
4
/
3
4
/
1
4
/
24. Îáîçíà÷åíèÿ íåêîòîðûõ ÷èñëîâûõ ìíîæåñòâ.
Îñíîâíûå ïîíÿòèÿ, ñâÿçàííûå ñ ìíîæåñòâàìè. Ïðè-
âåäåì îáîçíà÷åíèÿ ÷àñòî âñòðå÷àþùèõñÿ ÷èñëîâûõ
ìíîæåñòâ:
N ìíîæåñòâî íàòóðàëüíûõ ÷èñåë;
Z ìíîæåñòâî öåëûõ ÷èñåë;
Q ìíîæåñòâî ðàöèîíàëüíûõ ÷èñåë;
I ìíîæåñòâî èððàöèîíàëüíûõ ÷èñåë;
R ìíîæåñòâî äåéñòâèòåëüíûõ ÷èñåë;
Ñ ìíîæåñòâî êîìïëåêñíûõ ÷èñåë (ñì. ï. 45).
Åñëè à ÿâëÿåòñÿ ýëåìåíòîì ìíîæåñòâà À, òî ãîâî-
ðÿò, ÷òî à ïðèíàäëåæèò ìíîæåñòâó À è ïèøóò
Aa Î
(Î çíàê ïðèíàäëåæíîñòè).  ïðîòèâíîì ñëó÷àå,
ò. å. åñëè à íå ÿâëÿåòñÿ ýëåìåíòîì ìíîæåñòâà À,
ïèøóò
Aa Ï
. Òàê, íàïðèìåð,
NÎ5
, à
;NÏO
,5 ZÎ-
à
;4,1 ZÏ ,
3
2
QÎ
à
.2 QÏ
Íà ðèñ. 5 èçîáðàæåíû òî÷êè, çàäàííûå ïîëÿðíûìè
êîîðäèíàòàìè: À (1; 0),
,
2
;
5
3
÷
ø
ö
ç
è
æ
p
-B
.
4
3
;
2
1
÷
ø
ö
ç
è
æ
p
C
÷
ø
ö
ç
è
æ
p;
5
3
D
.
Çíàÿ ïîëÿðíûå êîîðäèíàòû òî÷êè, ìîæíî íàéòè
åå äåêàðòîâû êîîðäèíàòû ïî ôîðìóëàì
,sin,cos j=j= ryrx
(1)
íåïîñðåäñòâåííî âûòåêàþùèì èç îïðåäåëåíèÿ òðè-
ãîíîìåòðè÷åñêèõ ôóíêöèé (ñì. ï. 118). Íàîáîðîò, åñëè
èçâåñòíû äåêàðòîâû êîîðäèíàòû òî÷êè, òî åå ïîëÿð-
íûå êîîðäèíàòû íàõîäÿòñÿ ïî ôîðìóëàì
,
22
yxr +=
,
.sin
22
yx
y
r
y
+
-=
j
(2)
Ï ð è ì å ð. Íàéòè ïîëÿðíûå êîîðäèíàòû òî÷êè Ì
(4;
34
).
q Èñïîëüçóÿ ïåðâóþ èç ôîðìóë (2), íàõîäèì
.84816)34()4(
22
=+=+-=r Äàëåå, ñîãëàñíî
âòîðîé è òðåòüåé ôîðìóëàì (2), èìååì
,
2
1
8
4
cos =
-
=
j
,
2
3
8
34
sin ==j
îòêóäà ñëåäóåò, ÷òî
.
3
2p
=j
Èòàê,
.
3
2
;8
÷
ø
ö
ç
è
æ
p
M
n
0
,
Ðèñ. 5
cos j =
x
r
x
Ö
x
2
+ y
2
ÀËÃÅÁÐÀ
§ 3. Äåéñòâèòåëüíûå ÷èñëà
ÀËÃÅÁÐÀ
Ðàçäåë I. ×ÈÑËÀ
39
38
3
4
/
1
4
/
3
4
/
1
4
/
Ìíîæåñòâî, íå ñîäåðæàùåå íè îäíîãî ýëåìåíòà,
íàçûâàåòñÿ ïóñòûì (îáîçíà÷åíèå: Æ). Íàïðèìåð, ïó-
ñòûì ÿâëÿåòñÿ ìíîæåñòâî òî÷åê ïåðåñå÷åíèÿ äâóõ ïà-
ðàëëåëüíûõ ïðÿìûõ èëè ìíîæåñòâî äåéñòâèòåëüíûõ
êîðíåé óðàâíåíèÿ õ
2
+ 1 = 0.
Ìíîæåñòâî Â íàçûâàåòñÿ ïîäìíîæåñòâîì ìíî-
æåñòâà À, åñëè ëþáîé ýëåìåíò ìíîæåñòâà Â ïðèíàä-
ëåæèò ìíîæåñòâó À.  ýòîì ñëó÷àå ïèøóò
AB Ì
(
ÌÌ
ÌÌ
Ì çíàê âêëþ÷åíèÿ). Íàïðèìåð,
., RZZN ÌÌ
Îáúåäèíåíèåì ìíîæåñòâ À è Â íàçûâàåòñÿ ìíî-
æåñòâî, ñîñòîÿùåå èç òåõ è òîëüêî òåõ ýëåìåíòîâ, êî-
òîðûå ïðèíàäëåæàò õîòÿ áû îäíîìó èç ìíîæåñòâ À è
Â.  ýòîì ñëó÷àå ïèøóò:
BA U
(
U
çíàê îáúåäè-
íåíèÿ). Íàïðèìåð,
., RIQZZN == UU
Ïåðåñå÷åíèåì ìíîæåñòâ À è  íàçûâàåòñÿ ìíî-
æåñòâî, ñîñòîÿùåå èç âñåõ òåõ è òîëüêî òåõ ýëåìåí-
òîâ, êîòîðûå ïðèíàäëåæàò êàæäîìó èç ìíîæåñòâ
À è Â.  ýòîì ñëó÷àå ïèøóò:
BA I
(
I
çíàê ïå-
ðåñå÷åíèÿ). Íàïðèìåð,
== IQNZN II , Æ.
25. Ñðàâíåíèå äåéñòâèòåëüíûõ ÷èñåë. Äëÿ ëþ-
áûõ íåðàâíûõ äåéñòâèòåëüíûõ ÷èñåë à è b ìîæíî ñêà-
çàòü, êàêîå áîëüøå, à êàêîå ìåíüøå.
Ãîâîðÿò, ÷òî ÷èñëî à áîëüøå ÷èñëà b, è ïèøóò à > b,
åñëè ðàçíîñòü à b ïîëîæèòåëüíîå ÷èñëî; åñëè
ðàçíîñòü à b îòðèöàòåëüíîå ÷èñëî, òî ãîâîðÿò, ÷òî
÷èñëî à ìåíüøå ÷èñëà b, è ïèøóò à < b. Ñîãëàñíî
ýòîìó îïðåäåëåíèþ ëþáîå ïîëîæèòåëüíîå ÷èñëî áîëü-
øå íóëÿ, ëþáîå îòðèöàòåëüíîå ÷èñëî ìåíüøå íóëÿ è
ìåíüøå ëþáîãî ïîëîæèòåëüíîãî ÷èñëà. Äëÿ ëþáûõ
çàäàííûõ ÷èñåë à è b âåðíî îäíî è òîëüêî îäíî èç
ñîîòíîøåíèé à > b, a < b, a = b.
Ãåîìåòðè÷åñêè íåðàâåíñòâî a < b (à > b) îçíà÷àåò,
÷òî òî÷êà à ðàñïîëîæåíà íà êîîðäèíàòíîé ïðÿìîé
ëåâåå (ïðàâåå) òî÷êè b.
Çíàêè < , > íàçûâàþòñÿ çíàêàìè ñòðîãèõ íåðà-
âåíñòâ. Èíîãäà èñïîëüçóþòñÿ çíàêè íåñòðîãèõ íå-
ðàâåíñòâ
;, £³
çàïèñü
ba £
îçíà÷àåò, ÷òî âåðíî îäíî
èç äâóõ: èëè ÷èñëî à ìåíüøå ÷èñëà b, èëè ÷èñëî à
ðàâíî ÷èñëó b. Íàïðèìåð,
55,53 ³£
âåðíûå íå-
ðàâåíñòâà. Íåðàâåíñòâà à > b è c > d íàçûâàþòñÿ
íåðàâåíñòâàìè îäíîãî çíàêà; íåðàâåíñòâà à > b è
c < d íàçûâàþòñÿ íåðàâåíñòâàìè ïðîòèâîïîëîæ-
íûõ çíàêîâ. Åñëè ÷èñëà à, b, c òàêîâû, ÷òî a < b è
b < c, òî èñïîëüçóþò çàïèñü a < b < c, êîòîðóþ íàçûâà-
þò äâîéíûì íåðàâåíñòâîì.
26. Ñâîéñòâà ÷èñëîâûõ íåðàâåíñòâ. Äëÿ ëþáûõ
äåéñòâèòåëüíûõ ÷èñåë a, b, c, d âûïîëíÿþòñÿ ñëåäóþ-
ùèå ñâîéñòâà:
1
0
. Åñëè à > b, òî b < a.
2
0
. Åñëè à > b è b > c, òî à > ñ (ñâîéñòâî òðàíçè-
òèâíîñòè).
3
0
. Åñëè à > b, òî à + ñ > b + ñ.
4
0
. Åñëè à > b è ñ ïîëîæèòåëüíîå ÷èñëî (ñ > 0),
òî àñ > bñ (åñëè îáå ÷àñòè âåðíîãî íåðàâåíñòâà óì-
íîæèòü íà îäíî è òî æå ïîëîæèòåëüíîå ÷èñëî, òî
ïîëó÷èòñÿ âåðíîå íåðàâåíñòâî).
5
0
. Åñëè à > b è ñ îòðèöàòåëüíîå ÷èñëî (c < 0), òî
àñ < bñ (åñëè îáå ÷àñòè âåðíîãî íåðàâåíñòâà óìíî-
æèòü íà îäíî è òî æå îòðèöàòåëüíîå ÷èñëî è èçìå-
íèòü çíàê èñõîäíîãî íåðàâåíñòâà íà ïðîòèâîïîëîæ-
íûé, òî ïîëó÷èòñÿ âåðíîå íåðàâåíñòâî).
6
0
. Åñëè à > b è ñ > d, òî à + ñ > b + d (åñëè
ïî÷ëåííî ñëîæèòü äâà âåðíûõ íåðàâåíñòâà îäíîãî
çíàêà, òî ïîëó÷èòñÿ âåðíîå íåðàâåíñòâî).
ÀËÃÅÁÐÀ
§ 3. Äåéñòâèòåëüíûå ÷èñëà
ÀËÃÅÁÐÀ
Ðàçäåë I. ×ÈÑËÀ
39
38
3
4
/
1
4
/
3
4
/
1
4
/
Ìíîæåñòâî, íå ñîäåðæàùåå íè îäíîãî ýëåìåíòà,
íàçûâàåòñÿ ïóñòûì (îáîçíà÷åíèå: Æ). Íàïðèìåð, ïó-
ñòûì ÿâëÿåòñÿ ìíîæåñòâî òî÷åê ïåðåñå÷åíèÿ äâóõ ïà-
ðàëëåëüíûõ ïðÿìûõ èëè ìíîæåñòâî äåéñòâèòåëüíûõ
êîðíåé óðàâíåíèÿ õ
2
+ 1 = 0.
Ìíîæåñòâî Â íàçûâàåòñÿ ïîäìíîæåñòâîì ìíî-
æåñòâà À, åñëè ëþáîé ýëåìåíò ìíîæåñòâà Â ïðèíàä-
ëåæèò ìíîæåñòâó À.  ýòîì ñëó÷àå ïèøóò
AB Ì
(
ÌÌ
ÌÌ
Ì çíàê âêëþ÷åíèÿ). Íàïðèìåð,
., RZZN ÌÌ
Îáúåäèíåíèåì ìíîæåñòâ À è Â íàçûâàåòñÿ ìíî-
æåñòâî, ñîñòîÿùåå èç òåõ è òîëüêî òåõ ýëåìåíòîâ, êî-
òîðûå ïðèíàäëåæàò õîòÿ áû îäíîìó èç ìíîæåñòâ À è
Â.  ýòîì ñëó÷àå ïèøóò:
BA U
(
U
çíàê îáúåäè-
íåíèÿ). Íàïðèìåð,
., RIQZZN == UU
Ïåðåñå÷åíèåì ìíîæåñòâ À è  íàçûâàåòñÿ ìíî-
æåñòâî, ñîñòîÿùåå èç âñåõ òåõ è òîëüêî òåõ ýëåìåí-
òîâ, êîòîðûå ïðèíàäëåæàò êàæäîìó èç ìíîæåñòâ
À è Â.  ýòîì ñëó÷àå ïèøóò:
BA I
(
I
çíàê ïå-
ðåñå÷åíèÿ). Íàïðèìåð,
== IQNZN II , Æ.
25. Ñðàâíåíèå äåéñòâèòåëüíûõ ÷èñåë. Äëÿ ëþ-
áûõ íåðàâíûõ äåéñòâèòåëüíûõ ÷èñåë à è b ìîæíî ñêà-
çàòü, êàêîå áîëüøå, à êàêîå ìåíüøå.
Ãîâîðÿò, ÷òî ÷èñëî à áîëüøå ÷èñëà b, è ïèøóò à > b,
åñëè ðàçíîñòü à b ïîëîæèòåëüíîå ÷èñëî; åñëè
ðàçíîñòü à b îòðèöàòåëüíîå ÷èñëî, òî ãîâîðÿò, ÷òî
÷èñëî à ìåíüøå ÷èñëà b, è ïèøóò à < b. Ñîãëàñíî
ýòîìó îïðåäåëåíèþ ëþáîå ïîëîæèòåëüíîå ÷èñëî áîëü-
øå íóëÿ, ëþáîå îòðèöàòåëüíîå ÷èñëî ìåíüøå íóëÿ è
ìåíüøå ëþáîãî ïîëîæèòåëüíîãî ÷èñëà. Äëÿ ëþáûõ
çàäàííûõ ÷èñåë à è b âåðíî îäíî è òîëüêî îäíî èç
ñîîòíîøåíèé à > b, a < b, a = b.
Ãåîìåòðè÷åñêè íåðàâåíñòâî a < b (à > b) îçíà÷àåò,
÷òî òî÷êà à ðàñïîëîæåíà íà êîîðäèíàòíîé ïðÿìîé
ëåâåå (ïðàâåå) òî÷êè b.
Çíàêè < , > íàçûâàþòñÿ çíàêàìè ñòðîãèõ íåðà-
âåíñòâ. Èíîãäà èñïîëüçóþòñÿ çíàêè íåñòðîãèõ íå-
ðàâåíñòâ
;, £³
çàïèñü
ba £
îçíà÷àåò, ÷òî âåðíî îäíî
èç äâóõ: èëè ÷èñëî à ìåíüøå ÷èñëà b, èëè ÷èñëî à
ðàâíî ÷èñëó b. Íàïðèìåð,
55,53 ³£
âåðíûå íå-
ðàâåíñòâà. Íåðàâåíñòâà à > b è c > d íàçûâàþòñÿ
íåðàâåíñòâàìè îäíîãî çíàêà; íåðàâåíñòâà à > b è
c < d íàçûâàþòñÿ íåðàâåíñòâàìè ïðîòèâîïîëîæ-
íûõ çíàêîâ. Åñëè ÷èñëà à, b, c òàêîâû, ÷òî a < b è
b < c, òî èñïîëüçóþò çàïèñü a < b < c, êîòîðóþ íàçûâà-
þò äâîéíûì íåðàâåíñòâîì.
26. Ñâîéñòâà ÷èñëîâûõ íåðàâåíñòâ. Äëÿ ëþáûõ
äåéñòâèòåëüíûõ ÷èñåë a, b, c, d âûïîëíÿþòñÿ ñëåäóþ-
ùèå ñâîéñòâà:
1
0
. Åñëè à > b, òî b < a.
2
0
. Åñëè à > b è b > c, òî à > ñ (ñâîéñòâî òðàíçè-
òèâíîñòè).
3
0
. Åñëè à > b, òî à + ñ > b + ñ.
4
0
. Åñëè à > b è ñ ïîëîæèòåëüíîå ÷èñëî (ñ > 0),
òî àñ > bñ (åñëè îáå ÷àñòè âåðíîãî íåðàâåíñòâà óì-
íîæèòü íà îäíî è òî æå ïîëîæèòåëüíîå ÷èñëî, òî
ïîëó÷èòñÿ âåðíîå íåðàâåíñòâî).
5
0
. Åñëè à > b è ñ îòðèöàòåëüíîå ÷èñëî (c < 0), òî
àñ < bñ (åñëè îáå ÷àñòè âåðíîãî íåðàâåíñòâà óìíî-
æèòü íà îäíî è òî æå îòðèöàòåëüíîå ÷èñëî è èçìå-
íèòü çíàê èñõîäíîãî íåðàâåíñòâà íà ïðîòèâîïîëîæ-
íûé, òî ïîëó÷èòñÿ âåðíîå íåðàâåíñòâî).
6
0
. Åñëè à > b è ñ > d, òî à + ñ > b + d (åñëè
ïî÷ëåííî ñëîæèòü äâà âåðíûõ íåðàâåíñòâà îäíîãî
çíàêà, òî ïîëó÷èòñÿ âåðíîå íåðàâåíñòâî).
