Маслов А.В., Григорьева А.А. Математическое моделирование в экономике и управлении: Учебное пособие. Гриф УМО
Подождите немного. Документ загружается.


Исходная задача:
321min
52 xxxZ
.632
,55
,4
321
321
321
xxx
xxx
xxx
)3,2,1(0 jx
j
.
Двойственная задача:
321max
654 yyyf
.53
,25
,22
321
321
321
yyy
yyy
yyy
)3,2,1( 0 iy
i
.
Матрица коэффициентов ограничений в двойственной задаче
является транспонированной матрицей коэффициентов ограничений
исходной задачи.
Рассмотрим теперь случай, когда число ограничений не совпадает с
числом переменных.
Пример 4.8. Исходная задача. Найти минимальное значение
линейной функции
542
3xxxZ
при ограничениях
.5 3
,2 24
,1 2
652
5432
5421
xxx
xxxx
xxxx
)6,...,2,1(0 jx
j
.
,0,3,1,0,1,0 C
,
5
2
1
B
,
110
012
011
030
140
021
A
100
111
021
010
342
001
Т
A
.
Двойственная задача (несимметричная; вид (4.15)). Найти
максимальное значение линейной функции
321
52 yyyf
при
ограничениях
.0
,3
,12
,0
,1342
,0
3
321
21
2
321
1
y
yyy
yy
y
yyy
y
Вопросы для самопроверки
1. Задача линейного программирования в общем виде.
2. Возможные варианты решения задачи линейного
программирования.
3. Области применения линейного программирования.
4. Группы и подгруппы задач линейного программирования,
используемые в машиностроительной отрасли.
5. Пример решения станковой задачи.
6. Математическая модель задачи использования сырья.
71
1
2
3
5
4
6
7. Основные понятия и теоремы линейного программирования:
допустимый, опорный план, теорема связи опорных планов задачи
с угловыми точками выпуклого множества.
8. Формы записи задачи линейного программирования:
каноническая, стандартная, общая.
9. Нахождение решения задачи линейного программирования на
основе её геометрической интерпретации.
10. Свойства опорных решений задачи линейного
программирования.
11. Правила построения первоначальной симплекс-таблицы,
симплекс-таблицы, приведённой к какому-либо базису.
12. Признак оптимальности и другие утверждения на основе
приведённой симплекс-таблицы.
13. Алгоритм симплекс-метода решения задач линейного
программирования.
14. Правило перехода к новому базису для предотвращения
зацикливания симплекс-метода.
15. Метод искусственного базиса для отыскания начального
опорного решения.
16. Понятие двойственности в линейном программировании,
теоремы двойственности.
17. Виды математических моделей двойственных задач.
Тема 5 Целочисленное программирование
Значительная часть экономических задач, в частности, в
машиностроении, относящихся к задачам линейного программирования,
требует целочисленного решения. К ним относятся задачи, у которых
переменные величины означают количество единиц неделимой
продукции, например, распределение производственных заданий между
предприятиями, раскрой материалов, загрузка оборудования,
распределение судов по линиям, самолётов по рейсам, а также задачи по
производству неделимой продукции. Если единица составляет малую
часть всего объёма производства, то оптимальное решение находят
обычным симплексным методом, округляя его до целых единиц, исходя
из смысла задачи. В противном случае округление может привести к
решению, далёкому от оптимального целочисленного решения.
Постановка задачи и метод решения
72
1
2
3
5
4
6

Задача целочисленного программирования формулируется так же,
как и задача линейного программирования, но включается
дополнительное требование, состоящее в том, что значения
переменных, составляющих оптимальное решение, должны быть
целыми неотрицательными числами.
Найти минимальное значение линейной функции
n
j
jj
xcZ
1
(5.1)
при ограничениях
mibxa
ij
n
j
ij
,...,2,1 ,
1
,
(5.2)
),...,2,1(0 njx
j
(5.3)
j
x
целое. (5.4)
Предположим, что задача линейного программирования имеет
многогранник решений, приведённый на рис. 5.1.
Если наложить требование целочисленности, то допустимое
множество решений такой задачи представляет собой совокупность
изолированных целочисленных точек и не является выпуклым. Если
добавить новое ограничение, связывающее внешние целочисленные
точки, а затем в качестве многогранника решений использовать всё
выпуклое множество, ограниченное осями координат и новым контуром
(рис. 5.1), то получим новую задачу линейного программирования со
следующими свойствами:
Рис.5.1. Многогранник решений
1) новый многогранник решений содержит все целые точки,
заключавшиеся в первоначальном многограннике решений; любая его
угловая точка является целочисленной;
2) так как линейная функция достигает оптимума в угловой точке
многогранника решений, то построением такого многогранника и
обеспечивается целочисленность оптимального решения.
Это и есть графический способ решения задачи целочисленного
программирования. Но ясно, что он пригоден для решения таких задач,
73
1
2
3
5
4
6

где n-m=2, или, что более верно,
,2 rn
где n – число неизвестных, m
– число ограничений, r – ранг системы ограничений.
В общем же случае для определения оптимального плана задачи
(5.1)-(5.4) требуются специальные методы. В настоящее время
существует несколько таких методов, из которых наиболее известным
является метод Гомори, в основе которого лежит описанный выше
симплексный метод.
Метод Гомори
Процесс определения оптимального плана задачи целочисленного
программирования методом Гомори включает следующие основные этапы:
1. Используя симплекс-метод, находят решение задачи (5.1)-(5.3)
без учёта требования целочисленности переменных.
2. Составляют, если оптимальный план нецелочисленный,
дополнительное ограничение для переменной
,
i
x
которая в
оптимальном плане задачи (5.1)-(5.3) имеет максимальное дробное
значение (как это определяется, объясняется в примере). Как составлять
ограничение, также об этом отдельно.
3. Используя симплекс-метод (чаще всего, двойственная его
модификация, которая позволяет работать с отрицательными правыми
частями уравнений), находят решение задачи, получающейся из задачи
(5.1)-(5.3) в результате присоединения дополнительного ограничения.
4. В случае необходимости составляют ещё одно дополнительное
ограничение и продолжают итерационный процесс до получения
оптимального плана задачи (5.1)-(5.4) или установления её
неразрешимости (последнее имеет место в случае, если для дробного
i
x
все
j
i
x
в этой строке окажутся целыми).
Недостатком метода Гомори является требование
целочисленности для всех переменных: как основных, выражающих,
предположим, единицы продукции, так и для дополнительных,
выражающих величину неиспользованных ресурсов, которые могут
быть и дробными. Этот недостаток обходится в модификации метода,
рассмотренной И.Л. Акулич в книге "Математическое
программирование в примерах и задачах".
Составление дополнительного ограничения (сечения Гомори)
Пусть оптимальный план, полученный симплекс-методом для
задачи (5.1)-(5.3), следующий:
),...,,...,,...,,(
21 nmi
xxxxxx
и получен на
базисе
.,...,,...,,
21 mi
AAAA
Тогда последняя симплексная таблица имеет
следующий вид:
74
1
2
3
5
4
6

Таблица 5.1
Приведённая к базису симплексная таблица для задачи целочисленного
программирования
m
i
nm
niji
nj
nj
x
x
x
x
x...xx
......
x...xx
......
x...xx
xxx
X
mjm
m
m
m
...
...
...1...0...00
...........................
...0...1...00
...........................
...0...0...10
......0...0...01
2
1
1
1
122
111
1
1
1
1
Предположим, что
i
x
дробное; тогда некоторое
j
i
x
также
дробное (в противном случае задача не имеет целочисленного решения).
Обозначим через
i
x
и
ij
x
целые части чисел
i
x
и
j
i
x
, т.е.
наибольшие целые числа, не превосходящие числа
i
x
и
j
i
x
. Тогда
величины дробных частей
i
q
и
j
i
q
чисел
i
x
и
j
i
x
определяются как
разности:
,;
j
i
j
i
j
iiii
qxxqxx
где
i
q
и
.0
j
i
q
Например,
3
1
2
3
7
3
7
3
7
;3
3
7
,2
3
7
2
3
3
3
7
3
7
3
7
.
Так как по условию
),1( njx
j
– неотрицательные целые числа, то и
разность
0)...(
2
2
1
1
in
n
iii
qxqxqxq
также целое неотрицательное
число.
Преобразуя это неравенство в уравнение, вычитая из его левой
части целую неотрицательную дополнительную переменную
,
1n
x
умножим уравнение на –1, добавим к последней симплексной таблице
и, применяя симплексный метод (желательно двойственный), находим
новый план. Если он не является целочисленным, то по последней
симплексной таблице составляем новое дополнительное ограничение.
Если в оптимальном плане задачи (5.1)-(5.3) несколько дробных
,
i
x
то дополнительное ограничение составляют для max
i
q
. Это ускоряет
процесс получения оптимального целочисленного решения.
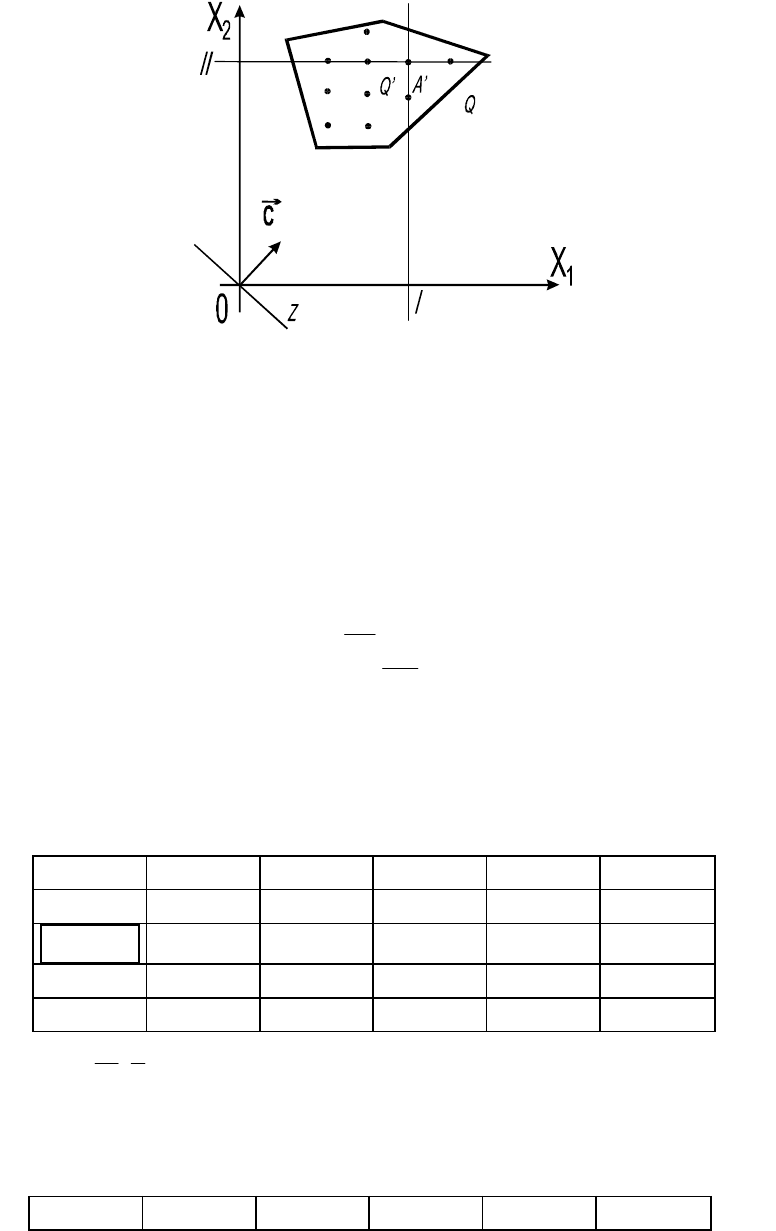
Рассмотрим геометрический смысл введения дополнительного
ограничения (см. рис. 5.2). Пусть в точке A многогранника решений Q
функция Z достигает максимального значения Z(A)=max, но координаты
точки A – дробные. Тогда введенные ограничения по целочисленности I
и II от области Q отсекают область
/
Q
с угловой точкой
/
A
,
75
1
2
3
5
4
6
координаты которой целочисленные и в которой линейная функция
достигает максимального значения.
Рис.5.2. Геометрический смысл ограничения Гомори
Метод Гомори рассмотрим на примере следующей задачи.
Пример 5.1. Найти максимальное значение функции
21
23 xxF
(5.5)
при условиях
,9 3
,6
,13=
521
421
321
xxx
xxx
xxx
(5.6)
,5,1,0 jx
j
(5.7)
j
x
– целые,
,5,1j
(5.8)
Дать геометрическую интерпретацию решения задачи.
Решение. Для определения оптимального плана задачи (5.5)-(5.8)
сначала находим оптимальный план задачи (5.5)-(5.7):
Таблица 5.2
Симплекс-таблица, приведённая к базису
543
,, AAA
x
1
x
2
x
3
x
4
x
5
1 1 1 0 0 13
1
-1 0 1 0 6
-3 1 0 0 0 9
3 2 0 0 1 0
,6
1
6
;
1
13
min
базис
,,,
543
AAA
план
)9;6;13;0;0(
1
–
неоптимальный,
41
AA
.
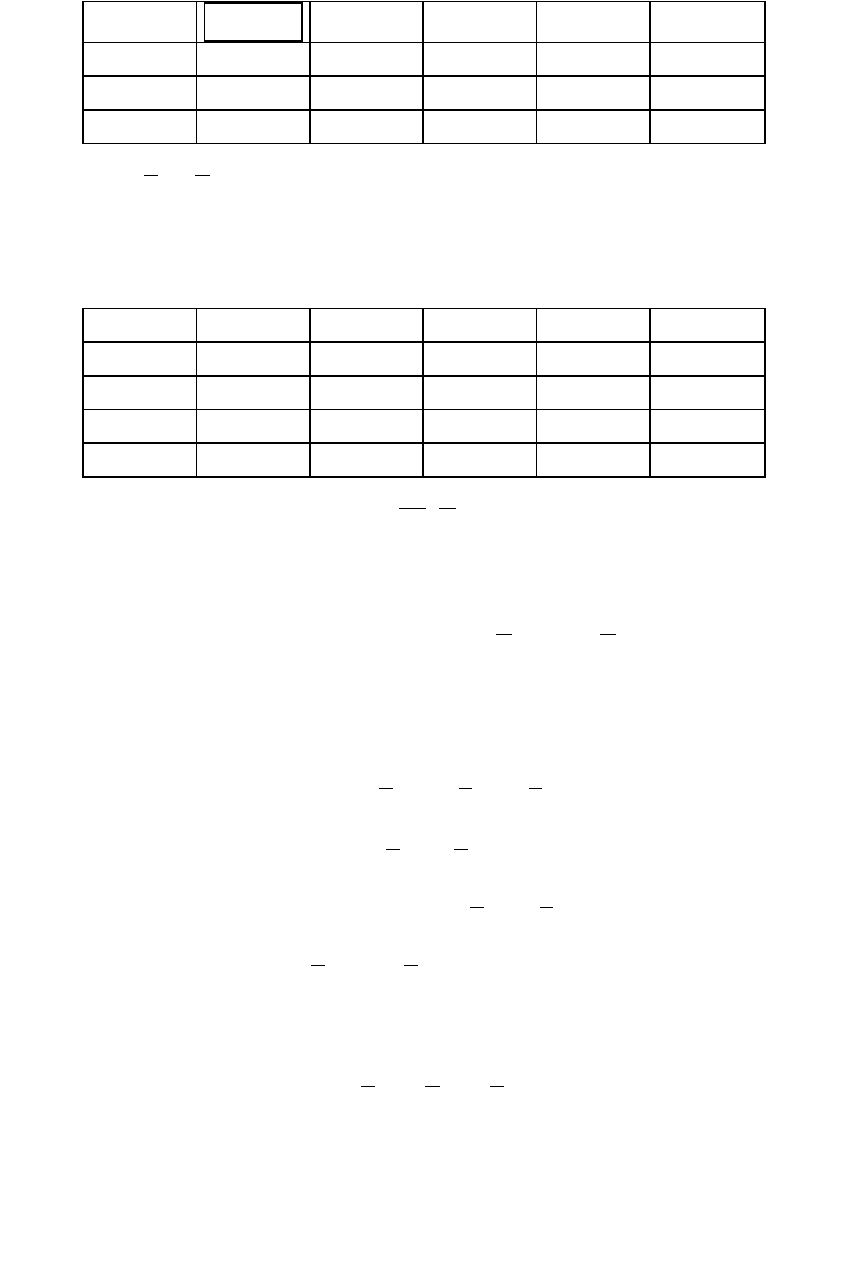
Таблица 5.3
Симплекс-таблица, приведённая к базису
531
,, AAA
x
1
x
2
x
3
x
4
x
5
76
1
2
3
5
4
6
0
2
1 -1 0 7
1 -1 0 1 0 6
0 -2 0 3 1 27
0 5 0 -3 0 -18
2
7
2
7
min
,
)27;0;7;0;6(
2
– неоптимальный, базис
531
,, AAA
,
23
AA
.
Таблица 5.4
Симплекс-таблица, приведённая к базису
521
,, AAA
x
1
x
2
x
3
x
4
x
5
0 1 1/2 -1/2 0 7/2
1 0 1/2 Ѕ 0 19/2
0 0 1 2 1 34
0 0 -5/2 -1/2 0 -71/2
Оптимальный план
34;0;0;
2
7
;
2
19
3
, базис
521
,, AAA
. Этот
оптимальный план не является оптимальным планом задачи (5.5)-(5.8),
поскольку две компоненты
1
x
и
2
x
имеют нецелочисленное значение.
При этом дробные части этих чисел
2
1
,
2
1
21
qq
равны между собой.
Поэтому для одной из этих переменных составляется дополнительное
ограничение. Составим, например, такое ограничение для переменной
2
x
(чаще берут первую строку). Из последней симплекс-таблицы имеем:
2
7
2
1
2
1
432
xxx
.
.
2
1
1
2
1
;
2
1
0
2
1
;011
;0;
2
1
3
2
7
4
2
3
2
2
2
5
2
1
2222
q
qq
qqxxq
Таким образом, к системе ограничений задачи (5.5)-(5.7) добавляем
неравенство
,
2
1
2
1
2
1
43
xx
т. е.
.1
43
xx
(5.9)
Теперь находим максимальное значение функции (5.5) при
выполнении условий (5.6), (5.7) и (5.9). В условие (5.9) вводим
дополнительную переменную
)1(0
6436
xxxx
:
Таблица 5.5
77
1
2
3
5
4
6
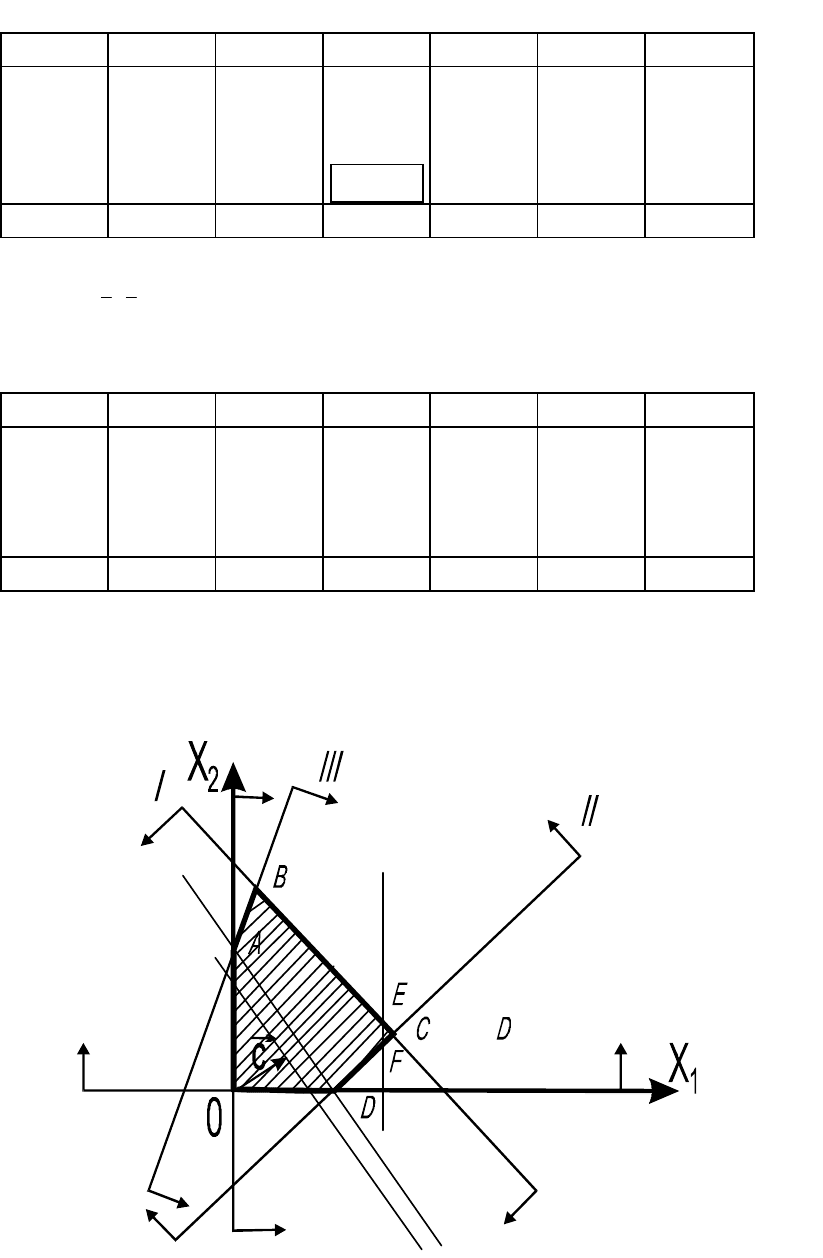
Ввод в симплекс-таблицу дополнительной переменной
6
x
x
1
x
2
x
3
x
4
x
5
x
6
0
1
0
0
1
0
0
0
1/2
1/2
1
1
-1/2
1/2
2
1
0
0
1
0
0
0
0
-1
7/2
19/2
34
1
0 0 -5/2 -1/2 0 0 -71/2
.1
1
1
;
1
1
min
Выберем
4
A
.
4
A
базис.
Таблица 5.6
Приведение симплекс-таблицы к базису
5421
,,, AAAA
x
1
x
2
x
3
x
4
x
5
x
6
0
1
0
0
1
0
0
0
1
0
-1
1
0
0
0
1
0
0
1
0
-1/2
1/2
2
-1
4
9
32
1
0 0 -2 0 0 -1/2 -35
Базис
5421
,,, AAAA
.
)32;1;0;4;9(
.
Запишем оптимальный план для исходной задачи:
).32;1;0;4;9(
*
x
При этом плане значение целевой функции равно
35
max
F
.
Геометрическая интерпретация решения задачи.
X
1
+
X
2
=
1
3
3
X
1
+
X
2
=
1
8
3
X
1
+
X
2
=
F
-
3
X
1
+
X
2
=
9
X
1
-
X
2
=
6
2
9
2
3
6
1
2
1
3
9
-
3
-
6
X
1
=
9
Рис.5.3. Геометрическая интерпретация решения задачи
78
1
2
3
5
4
6

Областью допустимых решений задачи (5.5)-(5.7) является
многоугольник ОАВСD (рис. 5.3). Из рисунка видно, что максимальное
значение целевая функция принимает в точке
,
2
7
;
2
19
C
т.е.
34;0;0;
2
7
;
2
19
x
является оптимальным планом. Так как этот план не
является оптимальным планом задачи (5.5)-(5.8) (числа
2
19
и
2
7
–
дробные), то вводится дополнительное ограничение
.1
43
xx
Исключая из этого неравенства
3
x
и
4
x
подстановкой вместо них
соответствующих значений из уравнений системы ограничений (5.6),
получим
9
1
x
.
91
6
13
143
214
213
xxx
xxx
xxx
.
Этому неравенству соответствует полуплоскость, ограниченная
прямой
,9
1
x
отсекающей от многоугольника ОАВСD треугольник EFC.
Как видно из рисунка, областью допустимых решений полученной
задачи является многоугольник OABEFD. В точке E(9;4) этого
многоугольника целевая функция данной задачи принимает
максимальное значение. Так как координаты точки Е – целые числа и
неизвестные
43
, xx
и
5
x
принимают целочисленные значения при
подстановке в уравнения (5.6) значений
9
1
x
и
,4
2
x
то
)32;0;0;4;9(
*
x
является оптимальным планом задачи (5.5)-(5.8). Это
следует и из таблицы симплекс-метода.
Замечание к использованию метода Гомори: если в
первоначальный базис задачи входили искусственные векторы, то при
составлении дополнительного ограничения искусственные переменные
необходимо опустить.
Вопросы для самопроверки
1. Области применения целочисленного программирования.
2. Постановка задачи целочисленного программирования.
3. Графический способ решения задачи целочисленного
программирования.
4. Алгоритм метода Гомори.
5. Правило составления дополнительного ограничения (сечения
Гомори).
6. Геометрический смысл введения сечения Гомори.
79
1
2
3
5
4
6
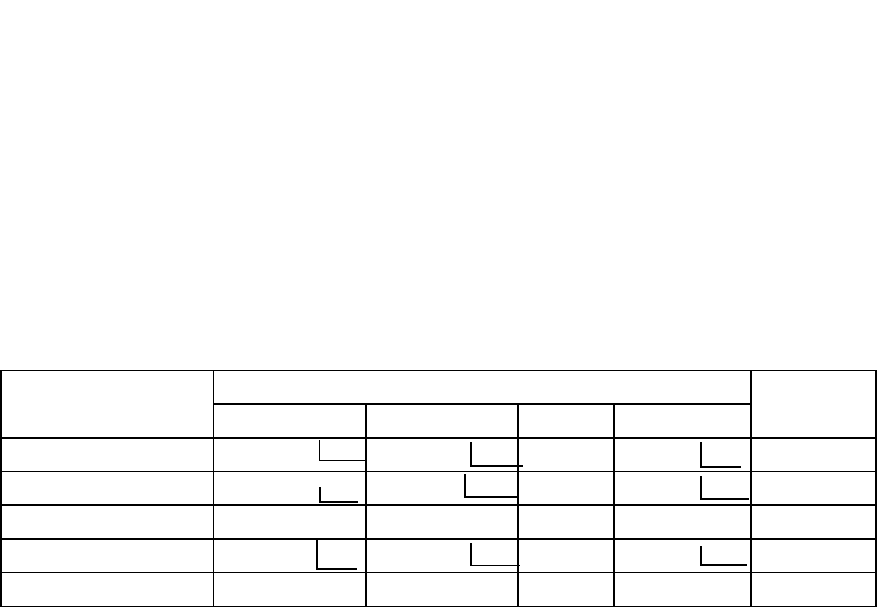
Тема 6 Транспортная задача
В настоящее время транспортная задача линейного
программирования широко применяется как в теоретических
разработках, так и в практике планирования различных экономических
процессов. Особенно важное значение она имеет при решении вопросов
рационализации поставок важнейших видов промышленной и
сельскохозяйственной продукции, а также оптимального планирования
грузопотоков и работы различных видов транспорта. Она применяется и
при решении экономических проблем, которые по своему характеру не
имеют ничего общего с транспортировкой груза, например,
оптимальное закрепление за станками операций по обработке деталей
("станковая" задача), проблема выбора (оптимального назначения),
задачи размещения производства с учётом транспортных и
производственных затрат.
В общем виде постановка транспортной задачи такова. (Сейчас
рассматривается классическая постановка задачи, её применение к
станковой задаче рассмотрим позже).
Пусть некоторый однородный продукт, сосредоточенный у m
поставщиков A
i
в количестве a
i
(i=1,2,…,m) единиц соответственно,
необходимо доставить n потребителям B
j
в количестве b
j
(
nj ,...,2,1
)
единиц. Известна стоимость c
ij
перевозки единицы груза от i-го
поставщика к j-му потребителю. Необходимо составить план перевозок,
позволяющий вывезти все грузы, полностью удовлетворить потребность
и добиться минимальной стоимости перевозок.
Обозначим через x
ij
количество единиц груза, запланированных к
перевозке от i-го поставщика к j-му потребителю; тогда условие задачи
можно записать в виде таблицы, которую в дальнейшем будем называть
матрицей планирования (табл. 6.1).
Таблица 6.1
Запись условий транспортной задачи
Поставщики Потребители Запасы
B
1
B
2
... B
n
A
1
x
11
С
11 x
12
C
12 ... x
1n
C
1n A
1
A
2
x
21
C
21 x
22
C
22 ... x
2n
C
2n A
2
... ... ... ... ... ...
A
m
x
m1
C
m1 x
m2
C
m2 ... x
mn
C
mn a
m
Потребности b
1
b
2
… b
n
∑a
i
=∑b
j
80
1
2
3
5
4
6
