Маслов А.В., Григорьева А.А. Математическое моделирование в экономике и управлении: Учебное пособие. Гриф УМО
Подождите немного. Документ загружается.


Каждое из неравенств системы ограничений задачи геометрически
определяет полуплоскость с граничными прямыми a
i1
x
1
+a
i2
x
2
=b
i
(i=1,
…,k), х
1
=0 и х
2
=0. В том случае, если система неравенств совместна,
область её решений есть множество точек, принадлежащих всем
указанным полуплоскостям. Так как множество точек пересечения
данных полуплоскостей выпуклое, то областью допустимых решений
задачи является выпуклое множество, которое называется
многоугольником решений (многогранником, когда n≥3). Стороны этого
многоугольника лежат на прямых, уравнения которых получаются из
исходной системы ограничений заменой знаков неравенств на знаки
точных равенств.
Таким образом, исходная задача линейного программирования
состоит в нахождении такой точки многоугольника решений, в которой
целевая функция L принимает максимальное значение (для стандартной
задачи линейного программирования). Эта точка существует тогда,
когда многоугольник решений не пуст, и на нём целевая функция
ограничена сверху. При указанных условиях в одной из вершин
многоугольника решений целевая функция принимает максимальное
значение. Для определения данной вершины построим линию уровня
с
1
х
1
+с
2
х
2
=h (где h – некоторая постоянная), проходящую через
многоугольник решений, и будем передвигать её в направлении вектора
c
=(с
1
;с
2
) до тех пор, пока она не пройдёт через последнюю её общую
точку с многоугольником решений. Координаты указанной точки и
определят оптимальный план данной задачи.
Заканчивая рассмотрение геометрической интерпретации задачи
линейного программирования, отметим, что при нахождении её
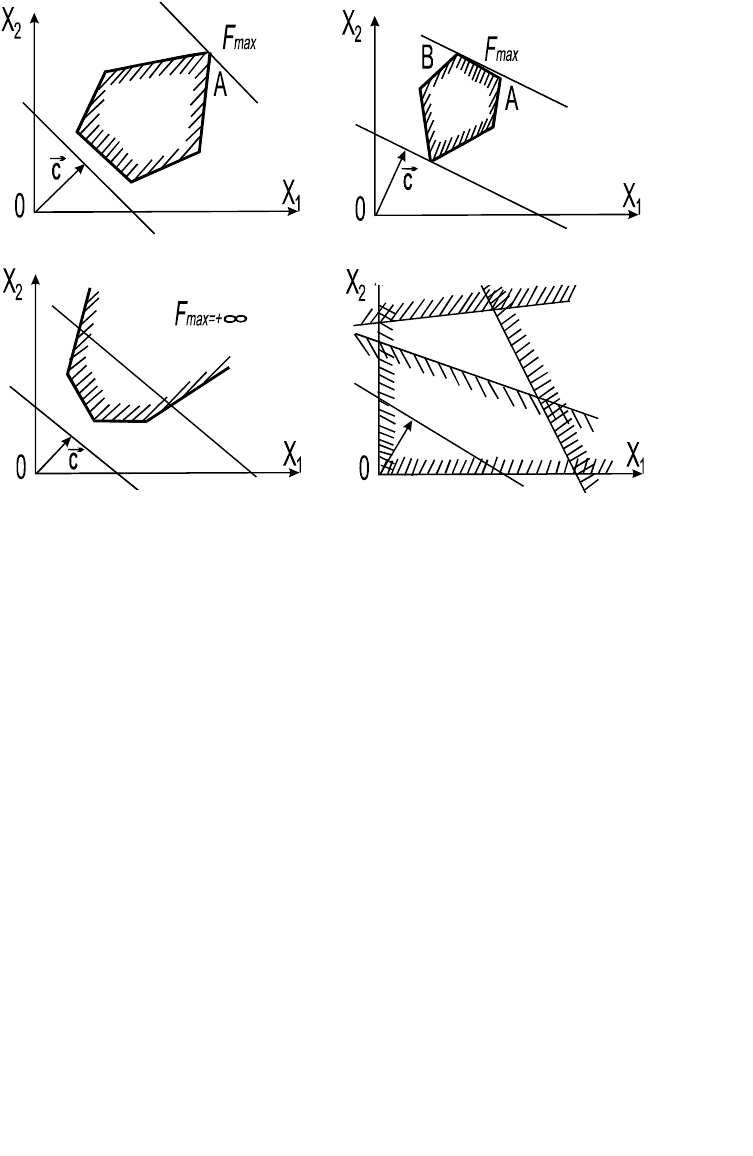
решения могут встретиться случаи, изображённые на рис. 4.1-4.4. Рис.
4.1 характеризует такой случай, когда целевая функция принимает
максимальное значение в единственной точке A.
Из рис. 4.2 видно, что максимальное значение целевая функция
принимает в любой точке отрезка AB. На рис. 4.3 изображен случай,
когда целевая функция не ограничена сверху на множестве допустимых
решений, а на рис. 4.4 – случай, когда система ограничений задачи
несовместна. Последние 3 случая – это особые случаи.
51
1
2
3
5
4
6
Отметим, что нахождение минимального значения линейной
целевой функции при данной системе ограничений отличается от
нахождения ее максимального значения при тех же ограничениях лишь
тем, что линия уровня с
1
х
1
+с
2
х
2
=h передвигается не в направлении
вектора
c
=(с
1
;с
2
), а в противоположном направлении. Таким образом,
отмеченные выше случаи, встречающиеся при нахождении
максимального значения целевой функции, имеют место и при
определении её минимального значения.
Итак, нахождение решения задачи линейного программирования на
основе её геометрической интерпретации включает следующие этапы:
1. Строят прямые, уравнения которых получают в результате
замены в ограничениях знаков неравенств на знаки точных равенств.
2. Находят полуплоскости, определяемые каждым из
ограничений задачи.
3. Находят многоугольник решений.
4. Строят вектор
c
=(с
1
;с
2
).
5. Строят прямую с
1
х
1
+с
2
х
2
=h, проходящую через
многоугольник решений.
6. Передвигают прямую с
1
х
1
+с
2
х
2
=h в направлении вектора
c
,
в результате чего-либо находят точку (точки), в которой целевая
функция принимает максимальное значение, либо устанавливают
неограниченность сверху функции на множестве планов.
7. Определяют координаты точки максимума функции и
вычисляют значение целевой функции в этой точке.
52
Рис.4.1. Случай 1
Рис. 4.2. Случай 2
Рис.4.3. Случай 3
Рис.4.4. Случай 4
1
2
3
5
4
6
Рассмотрим пример.
Пример 4.1. Для производства двух видов изделий А и В
предприятие использует три вида сырья. Норма расхода сырья каждого
вида на изготовление единицы продукции данного вида приведена в
таблице. В ней же указаны прибыль от реализации одного изделия
каждого вида и общее количество сырья данного вида, которое может
быть использовано предприятием.
Таблица 4.3
Условия задачи оптимального использования сырья
Вид сырья
Нормы расхода
сырья (кг)
на одно изделие
Общее
количество
A B сырья (кг)
I
II
III
12
4
3
4
4
12
300
120
252
Прибыль от
реализации одного
изделия (руб.)
30 40
Учитывая, что изделия А и В могут производиться в любых
соотношениях (сбыт обеспечен), требуется составить такой план их
выпуска, при котором прибыль предприятия от реализации всех
изделий является максимальной.
Решение. Предположим, что предприятие изготовит
1
x
изделий
вида А и
2
x
изделий вида В. Поскольку производство продукции
ограничено имеющимся в распоряжении предприятия сырьём каждого
вида, и количество изготовляемых изделий не может быть
отрицательным, должны выполняться неравенства:
.0,
,252123
,12044
,300412
21
21
21
21
xx
xx
xx
xx
Общая прибыль от реализации
1
x
изделий вида А и
2
x
изделий
вида В составит F=30
1
x
+ 40
2
x
.
Таким образом, мы приходим к следующей математической задаче:
среди всех неотрицательных решений данной системы линейных
неравенств требуется найти такое, при котором функция F принимает
максимальное значение.
Решим сформулированную задачу геометрическим способом.
Сначала определим многоугольник решений. Для этого в неравенствах
системы ограничений и условиях неотрицательности переменных знаки
53
1
2
3
5
4
6
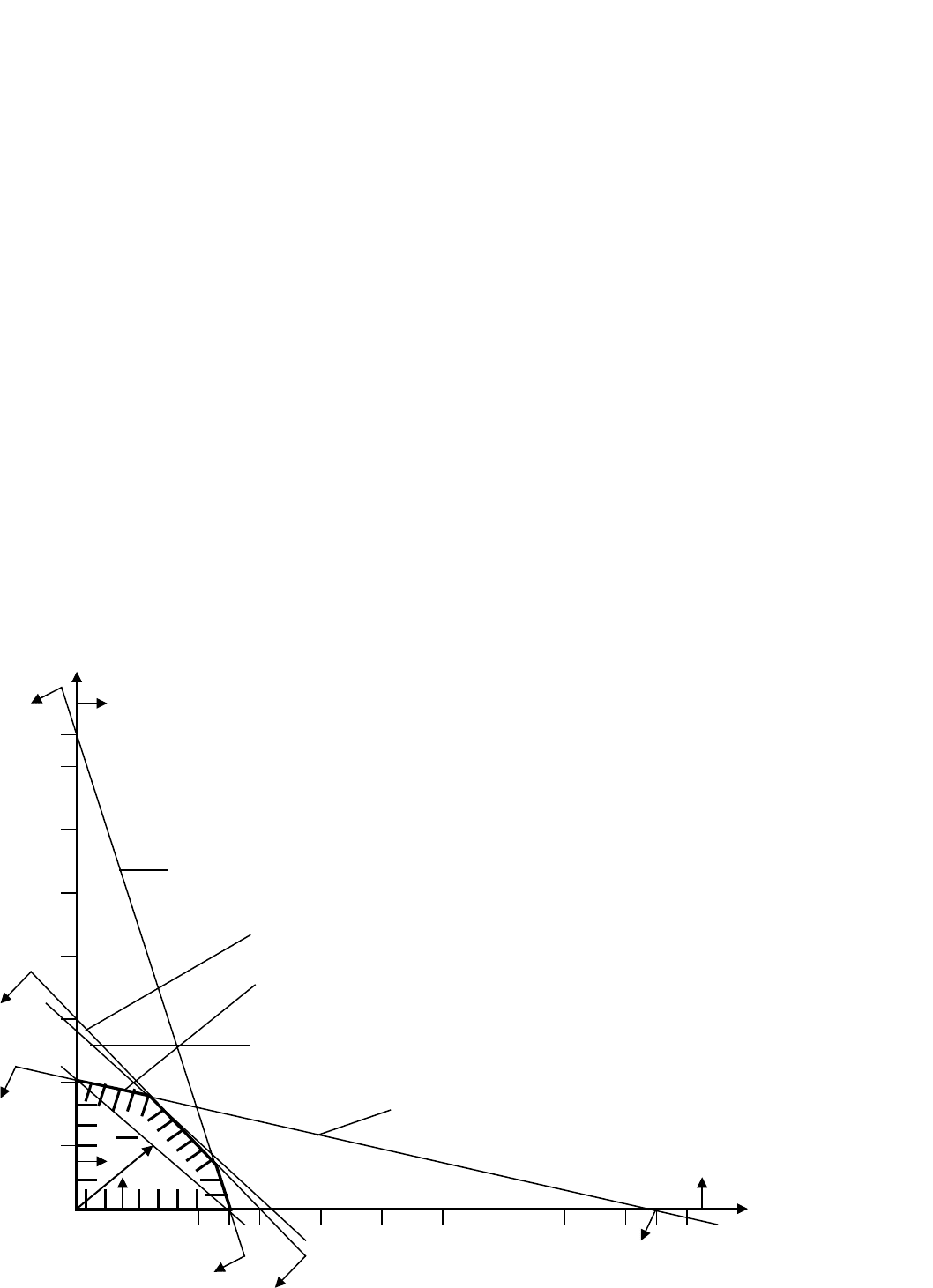
неравенств заменим на знаки точных равенств и найдём
соответствующие прямые:
Vx
IVx
IIIxx
IIxx
Ixx
,0
,0
,252123
,12044
,300412
2
1
21
21
21
Эти прямые изображены на рис. 4.5. Каждая из построенных
прямых делит плоскость на две полуплоскости. Координаты точек
одной полуплоскости удовлетворяют исходному неравенству, а другой
– нет. Чтобы определить искомую полуплоскость, нужно взять какую-
нибудь точку, принадлежащую одной из полуплоскостей, и проверить,
удовлетворяют ли её координаты данному неравенству. Если
координаты взятой точки удовлетворяют данному неравенству, то
искомой является та полуплоскость, которой принадлежит эта точка, в
противном случае – другая полуплоскость.
Найдем, например, полуплоскость, определяемую неравенством 12
1
x
+4
2
x
<300. Для этого, построив прямую 12
1
x
+4
2
x
=300 (пр. I),
возьмём какую-нибудь точку, принадлежащую одной из полученных
полуплоскостей, например, точку O(0;0). Координаты этой точки
удовлетворяют неравенству: 12
300040
, значит, полуплоскость,
которой принадлежит точка O(0;0), определится неравенством 12
3004
21
xx
.
Это и показано стрелками на рис. 4.5.
Пересечение полученных полуплоскостей и определяет
многоугольник решений данной задачи.
Как видно из рисунка, многоугольником решений является
пятиугольник OABCD. Координаты любой точки, принадлежащей
этому пятиугольнику, удовлетворяют данной системе неравенств и
условию неотрицательности переменных.
54
0
10 20
2
5
30 40 50 60 70 80 90 100
9
4
10
20
30
40
50
60
70
2
1
7
5
А
B
B
B
B
B
B
В
D
D
С
D
C
X
2
(V
(IV)
(II
)
12х
1
+ 4х
2
= 300 ( I )
4x
1
+ 4x
2
= 120 ( II )
30x
1
+ 40x
2
= 480
30x
1
+ 40x
2
= 1080
3x
1
+ 12x
2
=252 ( III )
X
1
1
2
3
5
4
6

Рис.4.5. Геометрический метод решения примера 4.1
Поэтому сформулированная задача будет решена, если мы сможем
найти точку, принадлежащую пятиугольнику OABCD, в которой
функция F принимает максимальное значение. Чтобы найти указанную
точку, построим вектор
)40;30(с
и прямую 30
hxx
21
40
, где h –
некоторая постоянная такая, что прямая 30
hxx
21
40
имеет общие
точки с многоугольником решений. Положим, например, h=480 и
построим прямую 30
48040
21
xx
(рис. 4.5). Точки пересечения с осями
0;16
12;0
.
Если теперь взять какую-нибудь точку, принадлежащую
построенной прямой и многоугольнику решений, то её координаты
определяют такой план производства изделий А и В, при котором
прибыль от их реализации равна 480 руб. Далее, полагая h равным
некоторому числу, большему чем 480, мы будем получать различные
параллельные прямые. Если они имеют общие точки с
многоугольником решений, то эти точки определяют план производства
изделий А и В, при которых прибыль от их реализации превзойдет 480
руб.
Перемещая построенную прямую 30
48040
21
xx
в направлении
вектора
с
, видим, что последней общей точкой её с многоугольником
решений задачи служит точка В. Координаты этой точки и определяют
план выпуска изделий А и В, при котором прибыль от их реализации
является максимальной.
Найдем координаты точки В как точки пересечения прямых II и III.
Следовательно, её координаты удовлетворяют уравнениям этих прямых:
.252123
,12044
21
21
xx
xx
Решив эту систему уравнений, получим
1
x
=12,
2
x
=18.
Следовательно, если предприятие изготовит 12 изделий вида А и 18
изделий вида В, то оно получит максимальную прибыль, равную
max
F
=
108018401230
руб.
55
B
B
B
B
B
B
В
D
D
1
2
3
5
4
6

Вообще, с помощью графического метода может быть решена такая
задача линейного программирования, система ограничений которой
содержит n неизвестных и m линейно независимых уравнений, если n и
m связаны соотношением n-m=2.
Действительно, пусть поставлена каноническая задача линейного
программирования: найти минимальное значение линейной функции
Z=
nn
xcxcxс ...
2211
при ограничениях
....
.............................................
,...
,...
2211
21222121
1212111
mnmnmm
nn
nn
bxaxaxa
bxaxaxa
bxcxaxa
,,...,2,1,0 njx
j
где все уравнения линейно независимы и выполняется соотношение n-
m=2.
Используя метод Гаусса, производим m исключений, в результате
которых базисными неизвестными оказались, например, m первых
неизвестных
m
xxx ,...,
21
, а свободными – два последних
1m
x
и
n
x
, т.е.
система ограничений приняла вид:
,
...
,
,
//
1
/
1
2
/
2
/
1
12
/
2
1
/
1
/
1
11
/
1
mnmnmmmm
n
n
m
m
n
n
m
m
bxaxax
bxaxax
bxaxax
(4.4)
0
j
x
(j=1,2,…,n).
С помощью уравнений преобразованной системы выражаем
линейную функцию только через свободные неизвестные и, учитывая,
что все базисные переменные - неотрицательные (
0
j
x
, j=1,2,…,n),
отбрасываем их, переходя к системе ограничений, выраженных в виде
неравенств. Таким образом, окончательно получаем следующую задачу:
Найти минимальное значение линейной функции Z=
nnmm
xcxс
/
1
/
1
при ограничениях
,
...................................
,
,
//
1
/
1
/
2
/
21
/
12
/
1
/
11
/
11
mnmnmmm
nnmm
nnmm
bxaxa
bxaxa
bxaxa
.0
,0
1
m
n
x
x
Преобразованная задача содержит две неизвестных; решая её
геометрическим способом, находим оптимальные значения
1m
x
и
n
x
, а
затем, подставляя их в (4.4), находим оптимальные значения
m
xxx ,...,,
21
.
Пример 4.2. Геометрическим способом найти оптимальный план
задачи линейного программирования, при котором линейная функция
54321
432 xxxxxZ
достигает максимального значения при
ограничениях
,381143823
,2242142
,42183
54321
54321
54321
xxxxx
xxxxx
xxxxx
(4.5)
.5,...,1,0 jx
j
56
1
2
3
5
4
6
Решение. Используя метод Гаусса, произведём три полных
исключения
321
,, xxx
. В результате приходим к системе
,2054
,70107
,63
543
542
54 1
xxx
xxx
xxx
откуда
.5420
,10770
,36
543
542
541
xxx
xxx
xxx
(4.6)
Подставляя эти значения в целевую линейную функцию и
отбрасывая в системе (4.5) базисные переменные, получаем задачу,
выраженную только через свободные неизвестные
4
x
и
5
x
:
найти максимальное значение линейной функции
38156
54
xxZ
при ограничениях
0,0
,2054
,70107
,63
54
54
54
54
xx
xx
xx
xx
(подставлены
значения из (4.6)).
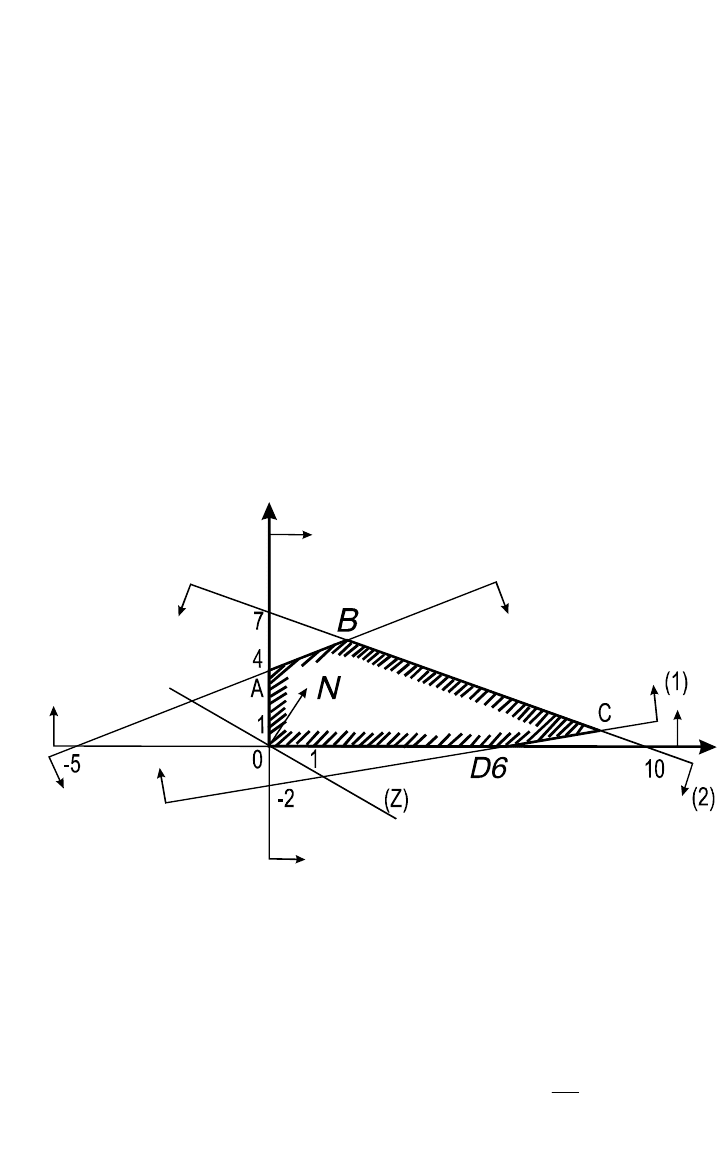
Рис.4.6. Геометрический метод решения примера 4.2
Построим многоугольник решений и линейную функцию в системе
координат
4
x
O
5
x
(рис. 4.6). Из рисунка заключаем, что линейная
функция принимает максимальное значение в угловой точке В, которая
лежит на пересечении прямых 2 и 3. В результате решения системы
,2054
,70107
54
54
xx
xx
находим:
2
4
x
,
5
28
5
x
.
Максимальное значение функции
max
Z
-38+12+84=58. Для
отыскания оптимального плана исходной задачи подставляем в (4.6)
57
1
2
3
5
4
6

найденные значения
4
x
и
5
x
. Окончательно получим:
5
104
1
x
;
0
2
x
;
0
3
x
;
2
4
x
;
5
28
5
x
.
Симплекс-метод решения задач линейного программирования
Рассмотрим задачу линейного программирования в
канонической форме и на минимум целевой функции:
min
1
j
n
j
j
xcf
BxA
j
n
j
j
1
,
0
j
x
,
nj ,...,2,1
,
(4.7)
где
nj
AAAA ,...,,...,,
21
– вектора условий задачи, а В – вектор
ограничений этой задачи. Любую задачу линейного программирования
можно свести к задаче линейного программирования в канонической
форме.
Допустимое решение
задачи (4.7) в канонической форме
называется опорным решением (планом) этой задачи, если векторы
условий
,,...,,
21 ikii
AAA
где
k
iii ,...,,
21
– номера всех ненулевых
координат
образуют линейно независимую систему векторов.
Пример 4.3. Например, векторы
)
2
5
;
2
1
;0;0(
1
и
)1;1;0;1(
2
являются допустимыми решениями задачи
Z=
min43
4321
xxxx
,222
,3
4321
4321
xxxx
xxxx
,0
j
x
1j
, 2, 3, 4.
Векторы условий
1
1
3
A
,
1
1
4
A
образуют, очевидно,
линейно независимую систему. Значит,
1
является опорным решением
данной задачи. Векторы
2
1
1
A
,
1
1
3
A
,
1
1
4
A
линейно зависимы, поэтому
2
не является опорным решением.
Свойства опорных решений
1. Если допустимое множество задачи (4.7) в канонической форме
не пусто, то эта задача имеет опорное решение.
2. Опорные решения задачи (4.7) являются крайними точками
допустимого множества этой задачи. (Допустимое множество всегда
выпукло.)
58
1
2
3
5
4
6

3. Задача (4.7) в канонической форме имеет лишь конечное число
различных опорных решений (либо не имеет их вовсе).
Чтобы найти некоторое опорное решение задачи (4.7), достаточно
выбрать базис системы
n
AAA ,...,,
21
векторов условий этой задачи так,
чтобы вектор ограничений В раскладывался по нему с
неотрицательными коэффициентами.
Если
r
iii
AAA ,...,,
21
– такой базис и
,...
2211 iririiii
dAdAdAB
,0,...,0,0
21
irii
ddd
то
)0;...0;;0;...;0;;0;...;0;;0;...;0(
21 r
iii
ddd
является опорным решением задачи (4.7).
Базис
r
iii
AAA ,...,,
21
системы векторов условий
n
AAA ,...,,
21
задачи
(4.7) называется базисом опорного решения
),...,;(
21 n
ddd
этой задачи,
если
0
i
d
при
r
iiii ,...,,
21
.
Пример 4.4. Рассмотрим опорное решение
)1;0;0;1(
задачи
min
4321
xxxxZ
02
,22
4321
4321
xxxx
xxxx
,0
j
x
.4,3,2,1j
Здесь
,
1
1
1
A
,
2
1
2
A
,
1
2
3
A
1
1
4
A
и
2141
,;, AAAA
базисы системы. Так как вторая и третья координаты
вектора
равны 0, то
41
, AA
является базисом опорного решения
. С
другой стороны, четвёртая координата
отлична от нуля.
Следовательно,
21
, AA
не будут базисом
.
У любого опорного решения задачи (4.7) не может быть более, чем
r ненулевых (положительных) координат, где r=rang(
n
AAA ,...,,
21
).
Опорное решение называется невырожденным, если число его
ненулевых координат точно равно r и вырожденным – в противном
случае.
Любое опорное решение имеет базис, при этом у невырожденного
опорного плана базис только один, а вырожденное опорное решение
может иметь несколько различных базисов.
Опорные решения играют важную роль при решении задач
линейного программирования в канонической форме, так как если
задача имеет оптимальное решение, то одно из её опорных решений
обязательно будет её оптимальным решением. Таким образом,
оптимальное решение задачи линейного программирования в
канонической форме можно искать только среди её опорных решений (а
их лишь конечное число).
По задаче линейного программирования в канонической форме
(4.7) всегда можно составить так называемую симплекс-таблицу:
59
1
2
3
5
4
6

Таблица 4.4
Исходная симплекс-таблица условий задачи линейного
программирования
х
1
х
2
... ... х
n
a
11
a
21
.
.
.
a
m1
a
12
a
22
.
.
.
a
m2
...
...
...
...
...
...
a
1n
a
2n
.
.
.
a
mn
b
1
b
2
.
.
.
b
m
- c
1
- c
2
... ... - c
n
0
Предположим, что
);...,;(
21 n
ddd
– некоторое опорное решение
задачи (4.7), а векторы
r
iii
AAA ,...,,
21
образуют его базис. Тогда таблицу
4.4 можно преобразовать методом Гаусса в таблицу 4.5.
Прибавим к последней строке таблицы 4.5 первую строку, умножив
на
1
i
с
, вторую строку, умножив на
2
i
c
, r-ю строку, умножив на
r
i
с
. В
результате получим новую таблицу 4.6, где
r
iii
ddd ,...,,
21
координаты
опорного решения, соответствующие векторам базиса
,,...,,
21 r
iii
AAA
где
,0...
21
r
iii
а
f
0
(значению целевой функции на опорном
решении
).
Таблица 4.6, полученная указанным выше способом, называется
симплекс-таблицей, приведённой к базису
r
iii
AAA ,...,,
21
опорного
решения
, а числа
nsiii
r
,...,,...,...,,...,,...,
21
1
оценками этого
базиса.
Имеют место следующие утверждения (рассматривается случай
задачи минимизации):
1. Если все оценки некоторого базиса опорного решения
неположительны, то оно является оптимальным решением задачи
линейного программирования в канонической форме (признак
оптимальности).
Таблица 4.5
Приведённая к базису
r
iii
AAA ,...,,
21
симплекс-таблица без изменений в
последней строке
x
1
... x
i1
... x
i2
... x
ir
... x
s
... x
n
a'
11
a'
21
.
1
0
.
0
1
.
0
0
.
a'
1s
a'
2s
.
a'
1n
a'
2n
.
d
i1
d
i2
.
60
1
2
3
5
4
6
