Маслов А.В., Григорьева А.А. Математическое моделирование в экономике и управлении: Учебное пособие. Гриф УМО

Подождите немного. Документ загружается.

Неструктуризованные проблемы отличаются значительной

неопределённостью и неформализуемостью как самих целей

деятельности, так и возможных программ действий. При решении этих

проблем суждения, опыт, интуиция руководителей, квалификация

специалистов, членов трудового коллектива приобретают решающее

значение. Научные методы решения таких проблем состоят в

использовании общих идей системного подхода в процессе

систематизации мыслительной деятельности при рассмотрении

проблем, а также в правильной организации экспертных опросов и

квалификационной обработке данных.

Эвристика (от греч. heuriskό – отыскиваю, открываю) –

совокупность знаний, опыта, интуиции, интеллекта, используемых для

получения решений с помощью неформальных правил и здравого

смысла.

К неструктуризованным проблемам можно, например, отнести

проблему формирования долгосрочных и среднесрочных планов научно

– исследовательских и опытно – конструкторских работ, построение

планов социального развития коллектива и т. п. В этих сферах какая бы

то ни было формализация выбора наилучших программ действий

наименее оправдана, хотя использование количественной информации и

проведение вспомогательных расчётов также может быть весьма

полезны.

Важно подчеркнуть, что отнесение той или иной проблемы к

одному из названных классов не носит постоянного характера. В

процессе всё более глубокого изучения, осмысления и анализа

проблемы она из неструктуризованной может превратиться в

слабоструктуризованную (при повышении удельного веса формально-

логического и математического описания проблемы и её элементов),

затем в хорошо структуризованную, а в ряде случаев и в стандартную

(сводимую к тривиальному ППР или к выполнению рутинных,

полностью автоматизируемых операций).

Часто решения стандартных и хорошо структуризованных проблем

называются программируемыми, а слабоструктуризованных и

неструктуризованных – непрограммируемыми.

Методы решения хорошо структуризованных проблем основаны на

применении математических моделей так называемого

оптимизационного программирования.

Остановимся на понятии модели, экономико-математической

модели, их классификации.

Моделирование как метод научного познания

Моделирование в научных исследованиях стало применяться ещё в

глубокой древности и постепенно захватывало всё новые области

научных знаний: техническое конструирование, строительство и

архитектуру, астрономию, классическую физику, химию, биологию и

социально-экономические науки. Большие успехи и признание

практически во всех отраслях современной науки принёс методу

моделирования ХХ век.

Однако методология моделирования долгое время развивалась

независимо в недрах отдельных наук. Отсутствовала единая система

понятий, единая терминология. Лишь постепенно стала осознаваться

роль моделирования как универсального метода научного познания.

Теперь же приходится сталкиваться уже с трудностями совершенно

другого рода. Понятия "модель" и "моделирование" стали настолько

употребительными, что зачастую сложно разобраться, где же кончается

мир моделей, и что в процессах познания не является моделированием.

Модель – это такой материально или мысленно представляемый

объект, который в процессе исследования замещает объект-оригинал

так, что его непосредственное изучение даёт новые знания об объекте-

оригинале.

Под моделированием понимается процесс построения, изучения и

применения моделей. Процесс моделирования обязательно включает и

построение абстракций, и умозаключения по аналогии, и

конструирование научных гипотез. Поэтому естественно задать вопрос:

является ли моделирование особым методом научного познания, не

является ли оно синонимом процесса теоретического исследования или

процесса познавательной деятельности вообще.

Главная особенность моделирования в том, что это метод

опосредованного познания с помощью объектов-заместителей. Модель

выступает как своеобразный инструмент для познания, который

исследователь ставит между собой и объектом, с помощью которого

изучает интересующий его объект. Необходимость использования

метода моделирования определяется тем, что многие объекты (или

проблемы, относящиеся к этим объектам) непосредственно исследовать

или вовсе невозможно (когда объект недосягаем, как, например, ядро

Земли и глубины Вселенной, либо еще реально не существует: будущее

состояние экономики, будущие потребности общества и т.п.), или это

исследование требует много времени и средств.

Процесс моделирования включает 3 элемента:

1) субъект (исследователь);

2) объект исследования;

3) модель, опосредствующую отношения познающего субъекта

и познаваемого объекта.

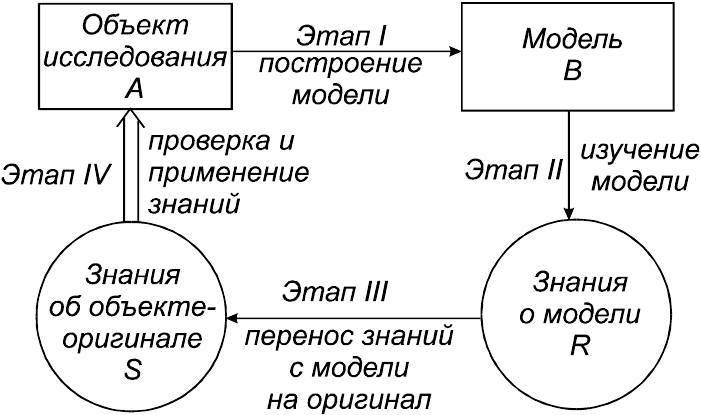
Сущность процесса моделирования схематически отображена на рис. 1.2.

Пусть имеется некоторый объект А, который необходимо

исследовать. Мы конструируем или находим в реальном мире другой

объект В – модель объекта А. Этап построения модели предполагает

наличие некоторых знаний об объекте–оригинале. Познавательные

возможности модели обусловливаются тем, что модель отображает

(воспроизводит, имитирует) какие-либо существенные черты объекта–

оригинала. Таким образом, изучение одних сторон моделируемого

объекта осуществляется ценой отказа от исследования других сторон.

Для одного объекта может быть построено несколько

специализированных моделей, концентрирующих внимание на

определённых сторонах исследуемого объекта или же характеризующих

объект с разной степенью детализации.

На втором этапе процесса моделирования модель выступает как

самостоятельный объект исследования. Одной из форм такого

исследования является проведение модельных экспериментов, при

которых сознательно изменяются условия функционирования модели и

систематизируются данные об её поведении. Конечным результатом

этого этапа является множество (совокупность) знаний о модели R.

Рис.1.2. Схема процесса моделирования

На третьем этапе осуществляется перенос знаний с модели на

оригинал–формирование множества знаний S. Одновременно мы

переходим с языка модели на язык оригинала. Этот процесс проводится

по определённым правилам. Знания о модели должны быть

скорректированы с учётом тех свойств объекта–оригинала, которые

нашли отражение или были изменены при построении модели.

Четвёртый этап – практическая проверка получаемых с помощью

моделей знаний и их использование для построения обобщающей

теории объекта, его преобразования или управления им. В итоге мы

снова возвращаемся к проблематике реального объекта.

Для понимания сущности моделирования важно не упускать из

виду, что моделирование – не единственный источник знаний об

объекте. Процесс моделирования как бы погружён в общий процесс

познания. Это обстоятельство учитывается не только на этапе

построения модели, но и на завершающей стадии, когда происходит

объединение и обобщение результатов исследования, получаемых на

основе многообразных средств познания.

Моделирование – циклический процесс. Это означает, что за

первым четырёхэтапным циклом может последовать второй, третий и

т.д. При этом знания об исследуемом объекте расширяются и

уточняются, а исходная модель постепенно достигает совершенства.

Всё множество моделей делится на два больших класса: модели

материальные (предметные) и модели идеальные (мысленные). Первые

воплощены в каких-либо материальных объектах, имеющих

естественное или искусственное происхождение (отобранные в природе

или созданные человеком для целей исследования); вторые – являются

продуктом человеческого мышления, операции с такими моделями

осуществляются в сознании человека.

В классе материальных (предметных) моделей можно выделить 2

основные группы: модели физические и модели предметно-

математические.

Нас интересуют последние модели. Они являются разновидностью

математических моделей. Предметно-математическое моделирование

основано на том, что характерные черты каких-либо процессов или

явлений, принципиально различных по своей физической природе,

могут выражаться одинаковыми математическими зависимостями.

Класс идеальных (мысленных) моделей объединяет довольно

разнообразные модели, различающиеся, прежде всего, по степени

формализации реальной действительности. В научном познании

основным видом идеальных моделей являются знаковые

(интуитивные) модели, использующие определённый

формализованный язык. В свою очередь важнейшим видом знаковых

моделей являются логико-математические модели, которые

выражаются на языке математики и логики. Логико-математическая

модель представляет собой определённую систему математических

отношений и логических выражений (функций, уравнений, неравенств,

алгоритмов и т.д.), отражающих существенные свойства исследуемого

объекта.

Предметно-математическое и логико-математическое

моделирование образуют математическое моделирование в широком

смысле – метод исследования, основанный на аналогии процессов и

явлений, различных по своей природе, но описываемых одинаковыми

математическими зависимостями. В современных научных

исследованиях математическое моделирование является, безусловно,

важнейшей формой моделирования, а в экономических исследованиях –

доминирующей формой. Роли двух разновидностей математических

моделей неодинаковы. Предметно-математические модели служат

средствами технической реализации логико-математических моделей и,

следовательно, предполагают существование последних.

Известно немало примеров построения наглядных и эффективно

действующих предметно-математических моделей для решения

разнообразных экономических задач. Ещё в XIX в. немецкий

экономист-географ Лаунхардт предложил механическую модель для

решения простейших задач размещения хозяйства; впоследствии эту

модель обобщил А. Вебер, и в историю экономической науки она вошла

как "штандортный треугольник Вебера". Для решения задач

межотраслевого баланса применяются гидравлические модели,

представляющие собой систему из заполняемых жидкостью

резервуаров и сообщающихся сосудов. Большое число электрических и

электронных моделей построено для изучения проблем регулирования

экономического роста, циркуляции денежных потоков, товарного

обращения и т.д. Далее мы будем изучать только логико-

математические модели (или просто математические модели).

Математическое моделирование полностью укладывается в

рассмотренную выше общую схему процесса моделирования.

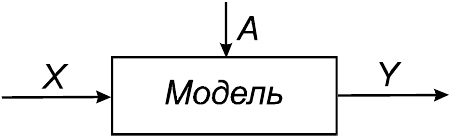
Математическая модель любого объекта (процесса, явления)

включает 3 группы элементов (рис. 1.3):

1) характеристики объекта, которые нужно определить

(неизвестные величины) – вектор Y=(y

);

2) характеристики внешних (по отношению к моделируемому

объекту) изменяющихся условий – вектор X=(x

);

3) совокупность внутренних параметров объекта А.

Множество условий и параметров X и A могут рассматриваться как

экзогенные величины (т.е. определяемые вне модели), а величины,

входящие в вектор Y, как эндогенные (т.е. определяемые с помощью

модели).

Рис.1.3. Входы и выходы модели

Математически модель можно интерпретировать как особый

преобразователь внешних условий объекта ("входа") Х в искомые

характеристики объекта ("выхода") Y. По способам выражения

соотношений между внешними условиями, внутренними параметрами и

искомыми характеристиками математические модели делятся на 2

основных типа: структурные и функциональные.

Структурные модели отражают внутреннюю организацию объекта:

его составные части, внутренние параметры, их связь с "входом" и

"выходом" и т.д.

Возможны 3 вида структурной модели:

1) хорошо структурированные, где все неизвестные

выражаются в виде явных функций от внешних условий и внутренних

параметров объекта;

= f

(A, X)

2) структурированные, где неизвестные определяются

совместно из системы известных отношений i-го вида (уравнений,

неравенств и т.д.);

(A, X, Y)=0

3) неструктурированные, где в модели включены

соотношения 2-го типа, но конкретный вид этих соотношений

неизвестен (модель как бы недостроена, определён только её каркас).

Модели 1-го и 2-го типа – это вполне определённые

математические задачи, которые можно решить по формульным или

численным алгоритмам. Модель 1-го типа даёт аналитическое решение.

Модели 3-го типа не сводятся к чётко определённым математическим

задачам и требуют нахождения особых средств для получения решений

(теория игр, исследование операций и пр.). Совокупность подходов и

методов к исследованию моделей рассматриваемого типа часто

объединяется термином "имитационное моделирование". Модель 3-го

типа даёт неотчётливое описание внутренней организации (структуры)

объекта и поэтому занимает промежуточное место между структурными

и функциональными моделями.

Основная идея функциональных моделей – познание сущности

объекта через важнейшие проявления этой сущности: деятельность,

функционирование, поведение. Функциональная модель имитирует

поведение объекта так, что, задавая значение "входа" X, можно

получить значение "выхода" Y (без участия информации об А): Y=D(X).

Построить функциональную модель – это значит отыскать оператор

D, связывающий X и Y.

Классификация экономико-математических моделей

Математические модели экономических процессов и явлений более

кратко можно назвать экономико-математическими моделями. Для

классификации этих моделей используют разные основания.

По целевому назначению экономико-математические модели

делятся на теоретико-аналитические, используемые в исследовании

общих свойств и закономерностей экономических процессов, и

прикладные, применяемые в решении конкретных экономических задач

(модели экономического анализа, прогнозирования, управления).

В соответствии с общей классификацией математических моделей

экономико-математические модели подразделяются на структурные и

функциональные, а также включают промежуточные формы

(структурно-функциональные). Типичными структурными моделями

являются модели межотраслевых связей. Функциональные модели –

модели поведения потребителей в условиях товарно-денежных

отношений.

Имеется также классификация моделей на дескриптивные и

нормативные. Дескриптивные модели отвечают на вопрос "Как это

происходит?" или "Как это может дальше развиваться?", т.е. они только

объясняют наблюдаемые факты или дают пассивный прогноз.

Нормативные модели отвечают на вопрос "Как это должно быть?", т.е.

предполагают целенаправленную деятельность. Таким образом,

дескриптивные и нормативные модели характеризуют принципиально

разные подходы к экономическому исследованию и экономической

практике. Примерами дескриптивных моделей являются некоторые

виды производственных функций и функций покупательного спроса.

Примеров эффективных нормативных моделей в экономике

машиностроения ещё мало.

По характеру отражения причинно-следственных связей различают

модели, жёстко детерминированные и модели, учитывающие

случайные и неопределённые факторы. Необходимо различать

неопределённость, описываемую вероятностными законами, и

неопределённость, для описания которой законы теории вероятностей

неприменимы. Второй тип неопределённости гораздо более сложен для

моделирования.

По способам отражения фактора времени экономико-

математические модели делятся на статические и динамические

модели. По форме математических зависимостей можно выделить

классы линейных и нелинейных моделей. По соотношению экзогенных и

эндогенных переменных, включаемых в модели, они могут разделяться

на открытые и закрытые модели. Полностью как открытых, так и

закрытых моделей не существует. Вопрос о преимуществах более

открытой или более закрытой модели решается по-разному в

зависимости от того, используется ли модель автономно или она входит

в некоторую систему моделей. Во втором случае предпочтение следует

отдать более открытой модели.

Существует классификация экономико-математических моделей и

по ряду других признаков: по типу используемых переменных – с

непрерывными переменными, дискретными и со смешанным составом

переменных; по степени детализации – агрегированные и

детализированные; по пространственному признаку – точечные и

пространственные и т.д.

Наряду с появлением новых типов моделей и новых признаков их

классификации осуществляется процесс интеграции моделей разного типа.

Этапы экономико-математического моделирования

Основные этапы моделирования уже были рассмотрены, но

поскольку в каждой отрасли знаний применение метода моделирования

имеет существенные особенности, целесообразно более внимательно

проанализировать и содержание этапов экономико-математического

моделирования.

1. Постановка экономической проблемы и её качественный

анализ.

Главное здесь – чётко сформулировать сущность проблемы,

принимаемые допущения (предпосылки) и те вопросы, на которые

требуется получить ответы. Этот этап включает выделение важнейших

черт и свойств моделируемого объекта и абстрагирование от

второстепенных; изучение структуры объекта и основных

зависимостей, связывающих его элементы; формулирование гипотез

(хотя бы предварительных), объясняющих поведение и развитие

объекта.

2. Построение математической модели.

Это этап формализации экономической проблемы (ситуации),

выражения её в виде конкретных математических зависимостей и

отношений (функций, уравнений, неравенств и т.п.). Обычно сначала

определяется основная конструкция (тип) математической модели и

изучаются возможности её применения, а затем уточняются детали этой

конструкции (конкретный перечень переменных и параметров, форма

связей). Таким образом, построение модели подразделяется, в свою

очередь, на несколько стадий.

Модель должна включать только основные факторы и условия,

характеризующие объект. Сложность модели должна быть в известном

смысле оптимальной. Неправильно полагать, что чем больше факторов

учитывает модель, тем она лучше работает и даёт лучшие результаты.

То же самое можно сказать о таких характеристиках сложности модели,

как используемые формы математических зависимостей (линейные и

нелинейные), учёт факторов случайности и неопределённости и т.д.

Одна из важных особенностей математических моделей –

потенциальная возможность их использования для решения

разнокачественных проблем. Поэтому, даже сталкиваясь с новой

экономической задачей, не нужно стремиться изобретать модель.

Вначале необходимо попытаться применить для решения этой задачи

уже известные модели.

3. Математический анализ модели.

Целью этого этапа является выяснения общих свойств модели (её

решений). Здесь применяются математические приёмы исследования.

Наиболее важный момент - доказательство существования решений в

сформулированной модели (теорема существования). Если удаётся

доказать, что математическая задача не имеет решения, то

необходимость в последующей работе по первоначальному варианту

модели отпадает; следует скорректировать либо постановку

экономической задачи, либо способ её математической формализации.

При аналитическом исследовании модели выясняются такие вопросы,

как, например, единственно ли решение, какие переменные

(неизвестные) могут входить в решение, каковы будут соотношения

между ними, в каких пределах и в зависимости от каких исходных

условий они изменяются, какова тенденция их изменения

(асимптотические свойства) и т.д. Преимущество аналитического

исследования по сравнению с эмпирическим (численным) в том, что

получаемые выводы сохраняют свою силу при различных конкретных

значениях внешних и внутренних параметров модели.

4. Подготовка исходной информации.

Это, пожалуй, наиболее трудоёмкий этап моделирования, отнюдь

не сводящийся к пассивному сбору исходных данных. Моделирование

предъявляет жёсткие требования к системе информации. В то же время

реальные возможности получения информации ограничивают выбор

моделей, предназначенных для практического использования. При этом

принимается во внимание не только принципиальная возможность

подготовки информации (за определённый срок), но и затраты на

подготовку соответствующих информационных массивов. Эти затраты

не должны превышать эффект от использования дополнительной

информации.

В процессе подготовки информации широко используются методы

теории вероятностей, теоретической и математической статистики

(определение генеральной совокупности, организация выборочных

обследований, оценка достоверности данных, определение наиболее

вероятных значений параметров регрессионного уравнения,

корреляционно-регрессионный анализ и т.п.).

5. Численное решение.

Этот этап включает разработку алгоритмов для численного

решения задачи, составление программ на ЭВМ и непосредственное

проведение расчётов. Трудности этого этапа обусловлены, прежде

всего, большой размерностью экономических задач, необходимостью

обработки значительных массивов информации. Обычно расчёты по

экономико-математической модели носят многовариантный характер.

Благодаря высокому быстродействию современных ЭВМ удаётся

проводить многочисленные модельные эксперименты, изучая поведение

модели при различных, плавных или резко меняющихся изменениях

некоторых условий. Исследование, проводимое численными методами,

может существенно дополнить результат аналитического исследования,

а для многих моделей оно является единственно осуществимым. Класс

экономических задач, которые можно решать численными методами,

значительно шире, чем класс задач, доступных аналитическому

исследованию.

6. Анализ численных результатов и их применение.

На этом заключительном этапе цикла встаёт труднейший вопрос о

правильности и полноте результатов моделирования, о степени

практической применимости последних.

Пока ещё не создано строгой теории проверки адекватности

экономико-математических моделей. Математические методы проверки

могут выявить некорректные построения моделей (доказывается

неразрешимость модели или не подтверждаются ранее принятые

статистические гипотезы) и тем самым сужать класс потенциально

правильных моделей. Неформальный анализ теоретических выводов и

численных результатов, получаемых посредством модели,

сопоставление их с имеющимися знаниями и фактами действительности