Маслов А.В., Григорьева А.А. Математическое моделирование в экономике и управлении: Учебное пособие. Гриф УМО

Подождите немного. Документ загружается.

2. Математическая постановка задач оптимизации и ее

интерпретация к проблемам выбора наилучших вариантов

экономического поведения.

3. Условия сведения экономической задачи к задаче оптимизации.

4. Классы задач математического программирования.

Тема 4 Линейное программирование

Рассмотрим ещё раз.общую задачу линейного программирования с

ограничением в форме уравнений и неравенств.

Под линейным программированием понимается отыскание

оптимального решения в задачах следующего вида:

Требуется найти экстремальное (максимальное или минимальное)

значение функции

xcxcxcL  ...

2211

(4.1)

при следующих линейных ограничениях:













,...

...

,...

2211

22222121

11212111

mnmnmm

bxaxaxa

(4.2)

njx

,...,1,0 

. (4.3)

Линейная функция L называется целевой функцией. В выражениях

(4.1) – (4.3) х

,х

,…,х

– искомые (неизвестные) величины. Ими могут

быть, в зависимости от вида задачи, количество изделий первого,

второго и т.д. типоразмера, количество материала соответствующей

марки, количество оборудования какой-либо группы и т.п.

Коэффициенты при неизвестных в целевой функции (4.1) с

, с

,… ,

– заданные постоянные величины. Их смысл также зависит от

решаемой задачи и может представлять собой себестоимость, цену или

прибыль от одного изделия соответствующего типоразмера, цену

оборудования, материалов, недогрузку оборудования во времени (в

часах) или отходы материала при раскрое и т.п. Проблема выбора

показателей, определяющих значения с

, с

,…,с

в целевой функции

(4.1), зависит от выбора критерия и показателя оптимальности решаемых

экономических задач.

Коэффициентами при неизвестных в линейных уравнениях (4.2)

являются числа a

, где i – номер уравнения или строки, в котором

находится данный коэффициент (i=1,2,…,m), j – номер неизвестной, при

которой стоит этот коэффициент (j=1,2,…,n) (номер столбца).

Коэффициенты a

являются заданными постоянными числами и

выражают те или иные затраты: времени на изготовление одного

изделия по одной группе оборудования, материала на изготовление одного изделия

и т.д.

Свободные члены в линейных неравенствах (4.2) b

(i=1,2,…,m)

обозначают, например, величину тех или иных ресурсов, которыми

располагают или могут располагать предприятия, экономический район

или народное хозяйство страны в целом. Ими может быть оборудование

или время его работы, запасы материалов, численность рабочих,

продолжительность рабочего времени и др. Выражение (4.3) означает,

что искомые переменные величины x

не могут быть отрицательными.

Каждое из решений системы (4.2) и (4.3) принято называть

возможным или допустимым планом.

Всё множество решений или допустимых планов называется

областью определения целевой функции. Она может оказаться пустой,

если условия (4.2) и (4.3) несовместны.

Из множества решений, удовлетворяющих условиям (4.2) и (4.3),

необходимо найти такое, при котором целевая функция (4.1) принимала

бы максимальное (или минимальное) значение.

Нахождение экстремума целевой функции (4.1) при условии, что

переменные удовлетворяют линейным ограничениям (4.2) и (4.3), и

составляет предмет линейного программирования.

При решении задач методом линейного программирования может

быть 3 случая:

1) условия задач (4.2) и (4.3) противоречивы, т.е. не

существует набора чисел х

, х

,…,х

, удовлетворяющих всем условиям

задачи;

2) условия (4.2) и (4.3) непротиворечивы, но целевая функция

не ограничена;

3) система условий (4.2) и (4.3) совместна, и экстремум

целевой функции существует, т.е. значение максимума или минимума

целевой функции (4.1) конечно.

Для большинства правильно поставленных практических задач

будет иметь место третий случай.

Область применения линейного программирования довольно

широка: от задачи составления рациона для кормления животных в

сельском хозяйстве до задачи оптимального использования сырья в

топливно-энергетической сфере хозяйства. Но нас будут в основном

интересовать задачи экономики машиностроительного производства,

решаемые методом линейного и вообще математического

программирования.

Данные задачи могут быть подразделены на две основные группы.

Первая группа – задачи, область применения которых ограничивается

отдельным предприятием. К ним относятся задачи, связанные:

1) с технологией производства или технологическим

планированием;

2) с оперативно-производственным планированием;

3) с технико-экономическим планированием.

В первую подгруппу входят задачи, получившие в литературе по

линейному программированию названия: станковая, раскройная и о

смесях. Это были задачи, решённые впервые методом линейного

программирования в 1939 г. в работе Л.В.Канторовича, пока

единственного российского учёного, удостоенного Нобелевской

премии по экономике в 1975 г. вместе с американским экономистом Т.

Купмансом за вклад в развитие теории оптимального распределения

ресурсов.

Станковая задача может быть отнесена и к задачам оперативно-

производственного планирования. Но, учитывая, что на

машиностроительных заводах она может применяться главным образом

для выбора оптимального варианта технологического процесса, её

целесообразнее рассматривать в первой подгруппе.

К задачам, связанным с оперативно-производственным

программированием (вторая подгруппа), относятся задачи по

оптимальному закреплению деталеопераций на рабочих местах.

В третью подгруппу включаются задачи по установлению

оптимальных годовых производственных программ (производственных

мощностей) предприятия, цеха, участка и оптимальному распределению

установленных программ по более коротким отрезкам времени -

кварталам и месяцам. Задачи этой подгруппы связаны также и с

оперативно-производственным планированием, главным образом при

определении оптимальной производственной мощности (в натуральных

единицах измерения) предприятия в целом и отдельных цехов, а также

производственной программы выпуска изделий по месяцам и кварталам

года.

Во вторую группу входят задачи, охватывающие отдельную

отрасль или народное хозяйство страны. К ним относятся задачи типа

транспортных, задачи по размещению и концентрации производства и

определению экономической эффективности капитальных вложений и

новой техники. К задачам этой группы примыкают и вопросы

составления межотраслевых балансов.

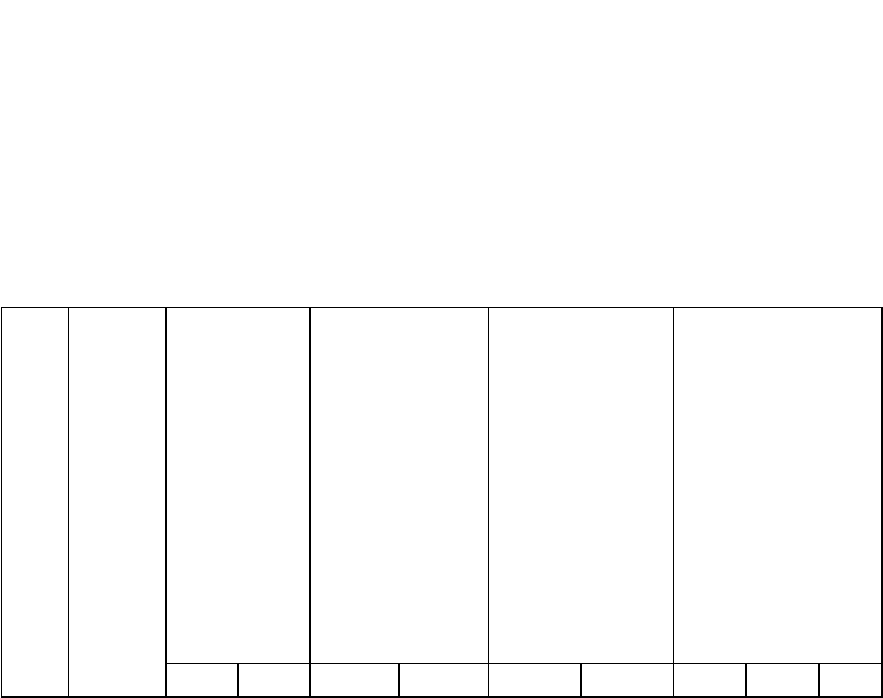
Рассмотрим станковую задачу кратко. Эту задачу впервые поставил

и решил методом разрешающих множителей Л. В. Канторович на

примере задачи фанерного треста.

Пусть имеются три группы однородного оборудования, на котором

необходимо обрабатывать два изделия (две детали). Количество единиц

оборудования в каждой группе и производительность при изготовлении

изделий каждой группы приведены в таблице 4.1.

Требуется определить, какое количество изделий каждого вида

нужно обрабатывать на каждой группе оборудования, или какое

количество единиц оборудования каждой группы нужно выделить,

чтобы изготовить максимальное количество изделий. Для упрощения в

этом примере принято, что нужно изготовить равное количество

изделий каждого вида.

Первое заключение, невольно напрашивающееся, заключается в

том, чтобы на каждой группе оборудования производилось одинаковое

количество изделий того и другого вида, которое и приведено в

таблице. Расчёт такого количества ведётся путем решения простейшей

системы линейных уравнений. Так, для первой группы оборудования

составляется система линейных уравнений:











2010

Здесь х – количество станков первой группы оборудования,

закреплённых за изделием 1, а у – за изделием 2.

Первое уравнение показывает, что нужно изготовить одинаковое

количество изделий первого и второго видов, а второе – что число

единиц этой группы оборудования, используемое для изготовления всех

изделий, равно трём.

Таблица 4.1

Пример решения станковой задачи

Гру

ппа

обо

ру-

дов.

Коли-

честв

о ед.

обору

д. в

групп

Произ-

водитель-

ность ед.

оборудо-

вания

Первый

вариант

решения (на

каждой

группе

изготавлива

ют

одинаковое

количество

изделий)

Оптимальны

й вариант

решения

(количество

изделий,

изготавливае

мых по

группам

оборудовани

я)

Оптимальный

вариант

решения

(количество ед.

оборудования,

занятых

изготовлением

изделий)

1-е 2-е 1-е 2-е 1-е 2-е 1-е 2-е Ито

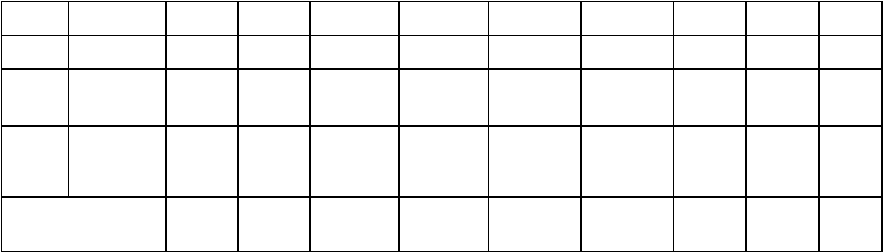
изд. изд. изд. изд. Изд. изд. изд. изд. го

I 3 10 20 20 20 26 6 8/3 1/3 3

II 3 20 30 36

(x=1,8)

(y=1,2)

60 - 3 - 3

III 1 30 80 21

(x=8/11)

21

(y=3/11)

- 80 - 1 1

Всего: 77 77 86 86 - - -

Решение этой системы линейных уравнений даёт х=2, а у=1, т.е. за

первым изделием нужно закрепить 2 единицы, а за вторым – одну

единицу оборудования первой группы. Суммарная производительность

оборудования этой группы, соответствующая данному закреплению, и

показана в таблице 4.1 в столбцах первого варианта решения.

Вычислим отношение производительностей по второму и первому

изделиям для каждой группы оборудования и расположим их в порядке

убывания (или возрастания) – 8/3(III), 2(I) и 3/2(II). Для группы, у

которой это отношение имеет наибольшую величину, все единицы

оборудования закрепим за вторым изделием, а у которой это отношение

наименьшее – за первым. В оставшейся группе оборудование

распределяется так, чтобы выровнять суммарное производство по

изделию каждого вида. В данном примере это означает, что III группу

оборудования, у которой отношение производительностей

максимальное (8/3), нужно целиком закрепить за вторым изделием, а II

группу с наименьшим отношением производительностей – за первым

изделием. Группа I распределяется так, чтобы выровнять объём

производства по обоим изделиям.

Для данного примера это выравнивание происходит путём решения

системы двух линейных уравнений с двумя неизвестными.

Первое уравнение составляют так, чтобы количество первого и

второго изделий, изготовляемое на всех группах оборудования, было

одинаковым. В данном случае получим

10х+60=20у+80,

где х и у – количество единиц оборудования I группы, закреплённое

соответственно за первым и вторым изделиями.

Второе уравнение составляется исходя из условия, что суммарное

количество единиц оборудования I группы, закреплённое за первым и

вторым изделиями, не должно превышать имеющегося количества, т.е.

для данного случая х+у=3.

Найденное оптимальное решение позволяет увеличить выпуск

изделий до 86, что по сравнению с первым возможным вариантом дает

увеличение на 11,7% без каких-либо дополнительных затрат.

Одновременно это приведёт и к снижению себестоимости изготовленных

изделий.

Для задач большего объёма (с большим числом групп

оборудования и видов изделий) найти решение значительно труднее и

возможно лишь с использованием методов линейного

программирования.

Запишем задачу в следующем виде:

максимизировать целевую функцию

L=10x

+20x

+30x

→max

при условиях















0)803020(302090

32221 2312111

3231

2221

1211

xxxxxx

),3,2,1;2,1(0  ijx

где x

– количество единиц оборудования i-й группы, занятое

изготовлением изделий j-го вида.

Если количество изделий каждого вида будет задано (что чаще

практически и имеет место), то станковая задача может быть поставлена

в другом виде. Вместо максимизации количества выпускаемых изделий

в этом случае нужно найти минимум времени на производство всех

изделий, т.е. минимум целевой функции

min







),,...,1;,...,1(,0

),,...,3,2(0

...

222

111

njmix

mixx

Nxa

ninin



































где х

– время, затрачиваемое i-й группой оборудования на изготовление

изделий j-го вида;

– суммарная производительность всех единиц оборудования i-й

группы в единицу времени при изготовлении изделий j-го вида;

– заданное количество изделий j-го вида, которое требуется

изготовить.

Так, если для рассматриваемого примера будет задано, что

=50, то задача запишется так:

минимизировать L=x

при условиях:

).2,1;3,2,1(0

,0)(

,50809060

,50306030

32312211

22211211

322312

312111

















jix

xxxx

xxx

В такой задаче вместо групп оборудования могут быть взяты

отдельные участки, цехи и предприятия в целом, если они выпускают

одни и те же изделия. В этом случае задача ничем не будет отличаться

от изложенной выше.

Для постановки и решения станковой задачи необходимо знать

производительности или нормы времени на изготовление изделий по

каждой группе оборудования, т.е. иметь нормы времени для всех

технологических процессов, по которым будут изготавливаться эти

изделия. На практике же это бывает очень редко.

Эта задача в несколько изменённом виде используется также при

распределении производственной программы между предприятиями,

точнее, при решении задач по размещению и концентрации производства.

Задача оптимального раскроя материала (задача по раскрою)

является одним из частных случаев задачи по оптимальному

использованию комплексного сырья.

Математическую модель задачи оптимального использования

сырья можно представить в следующем виде.

Пусть выпускается n видов продукции, используется m видов

сырья. Обозначим через S

(i=1,…,m) виды сырья; b

– запасы сырья i-го

вида; P

(j=1,…,n) – виды продукции; a

– количество единиц i-го сырья,

идущего на изготовление единицы j-й продукции; с

– величину

прибыли, получаемой при реализации единицы j-й продукции.

Условия задачи запишем в таблице 4.2.

Пусть x

– количество единиц j-й продукции, которое необходимо

произвести. Сама модель:

найти максимальное значение линейной функции

Z=c

+ +c

+…+c

при ограничениях













,...

...

,...

2211

22222121

11212111

mnmnmm

bxaxaxa

.,...,2,1,0,,...,1,0 mibnjx



где a

– количество сырья, расходуемое на изготовление единицы

продукции, b

– общее количество сырья i-го вида, c

– величина

прибыли, получаемой с единицы j-й продукции.

Система ограничений и функция цели составляют математическую

модель рассматриваемой экономической задачи.

Как мы уже выясняли, допустимым решением (или планом) задачи

линейного программирования является совокупность чисел х=(х

,х

…,х

), удовлетворяющих ограничениям задачи. План х

=(х

,х

,…,х

при котором целевая функция задачи принимает своё максимальное

(минимальное) значение, называется оптимальным.

Таблица 4.2

Условия задачи оптимального использования комплексного сырья

Количество единиц i-го сырья, идущего на

Виды Запасы изготовление единицы j-й продукции

сырья сырья P

... P

... a

... ... ... ... ... ...

... a

Прибыль с

... с

Форма записи задачи линейного программирования может быть

различной. Стандартной (или симметричной) задачей линейного

программирования называется задача, которая состоит в определении

максимального значения целевой функции при выполнении условий в

виде системы неравенств и неотрицательности переменных.

Канонической (или основной) задачей линейного программирования

называется задача, которая состоит в определении минимального

значения целевой функции при выполнении условий в виде системы

линейных уравнений и неотрицательности переменных. В общей задаче

линейного программирования могут быть условия, как в виде системы

неравенств, так и в виде равенств, причем не на все переменные может

быть наложено условие неотрицательности:

),,...,1( 0 nkkjx



Указанные выше три формы записи задачи линейного

программирования эквивалентны в том смысле, что каждая из них с

помощью несложных преобразований может быть переписана в форме

другой задачи. Для этого необходимо уметь, во-первых, сводить задачу

минимизации функции к задаче максимизации, во-вторых, переходить

от ограничений – неравенств к ограничениям – равенствам и наоборот,

в-третьих, заменять переменные, которые не подчинены условию

неотрицательности.

В том случае, когда требуется найти функцию L=c

+…+c

можно перейти к нахождению максимума функции L

= -L= -c

-c

-…

-c

, поскольку min L

= -max(-L).

Ограничение-неравенство исходной задачи линейного

программирования, имеющее вид "≤", преобразовать в ограничение-

равенство можно добавлением к его левой части дополнительной

неотрицательной переменной, а ограничение-неравенство вида "≥" – в

ограничение-равенство вычитанием из его левой части дополнительной

неотрицательной переменной. Таким образом, ограничение-неравенство

+…+a

≤b

преобразуется в ограничение-равенство

+…+a

n+1

≥0),

а ограничение-неравенство

+…+a

≥b

– в ограничение-равенство

+…+a

-x

n+1

≥0).

В то же время каждое уравнение системы ограничений может быть

представлено так:











....

,...

211

2211

ininii

bxaaxa

bxaxaxa

Число вводимых дополнительных неотрицательных переменных

при преобразовании ограничений-неравенств в ограничения-равенства

равно числу преобразуемых неравенств.

Вводимые дополнительные переменные имеют вполне

определённый экономический смысл. Так, если в ограничениях

исходной задачи линейного программирования отражается расход и

наличие производственных ресурсов, то числовое значение

дополнительной переменной в плане задачи, записанной в форме

основной, равно объёму неиспользованного соответствующего ресурса.

Отметим, наконец, что если переменная х

не подчинена условию

неотрицательности, то её следует заменить двумя неотрицательными

переменными u

и v

, приняв x

-v

Рассмотрим каноническую задачу линейного программирования.

Перепишем её в векторной форме: найти минимум функции L=CX при

условиях A

+…+A

=B, (*)

где C=(с

;с

;…;с

), X=(х

;х

;…;х

); CX – скалярное произведение

векторов; А

,…,А

и В – m-мерные вектор-столбцы, составленные из

коэффициентов при неизвестных и свободных членах системы уравнений

задачи:

























































mmm

...

;...;

...

;

...

;

...

Определение 4.1. План X=(х

;х

;…х

) называется опорным планом

канонической задачи линейного программирования, если система

векторов A

, входящих в разложение (*) с положительными

коэффициентами, линейно независима.

Так как векторы A

являются m-мерными, то из определения

опорного плана следует, что число его положительных компонент не

может быть больше, чем m.

Опорный план называется невырожденным, если он содержит

ровно m положительных компонент, в противном случае он называется

вырожденным.

Свойства канонической задачи линейного программирования

тесным образом связаны со свойствами выпуклых множеств.

Теорема 4.1. Множество планов канонической задачи линейного

программирования является выпуклым (если оно не пусто). Непустое

множество планов канонической задачи линейного программирования

называется многогранником решений, а всякая угловая точка

многогранника решений – вершиной.

Теорема 4.2. Если каноническая задача линейного

программирования имеет оптимальный план, то максимальное

(минимальное) значение целевая функция задачи принимает в одной из

вершин многогранника решений. Если максимальное (минимальное)

значение целевая функция задачи принимает более, чем в одной

вершине, то она принимает его во всякой точке, являющейся выпуклой

линейной комбинацией его вершин.

Теорема 4.3. Если система векторов А

,А

,…,А

(k≤n) в разложении

(*) линейно независима и такова, что А

+А

+…+А

=B, где все x

≥0,

то точка X=(х

;х

;…;х

;0;…;0) является вершиной многогранника решений.

Теорема 4.4. Если X=(х

;х

;…х

) – вершина многогранника решений,

то вектора A

, соответствующие положительным x

в разложении (*),

линейно независимы.

Сформулированные теоремы позволяют сделать следующие выводы.

Непустое множество планов канонической задачи линейного

программирования образуют выпуклый многогранник. Каждая вершина

этого многогранника определяет опорный план. В одной из вершин

многогранника решений (т.е. для одного из опорных планов) значение

целевой функции является максимальным (минимальным) при условии,

что функция ограничена сверху (снизу) на множестве планов. Если

экстремальное значение функции принимает значение более, чем в

одной вершине, то это же значение она принимает в любой точке,

являющейся выпуклой линейной комбинацией данных вершин, т. е. на

отрезке.

Вершину многогранника решений, в которой целевая функция

принимает экстремальное значение, найти сравнительно просто, если

задача, записанная в форме стандартной, содержит не более 2-х

переменных или задача, записанная в форме канонической, содержит не

более 2-х свободных переменных, т.е. n-r≤2, где n – число переменных,

r – ранг матрицы, составленной из коэффициентов в системе ограничений

задачи.

Найдём решение задачи (записанной в форме стандартной),

состоящей в определении максимального значения функции L=c

при условиях

+ +a

≤b

(i=1,…,k),

≥0 (j=1,2).