Маслов А.В., Григорьева А.А. Математическое моделирование в экономике и управлении: Учебное пособие. Гриф УМО
Подождите немного. Документ загружается.

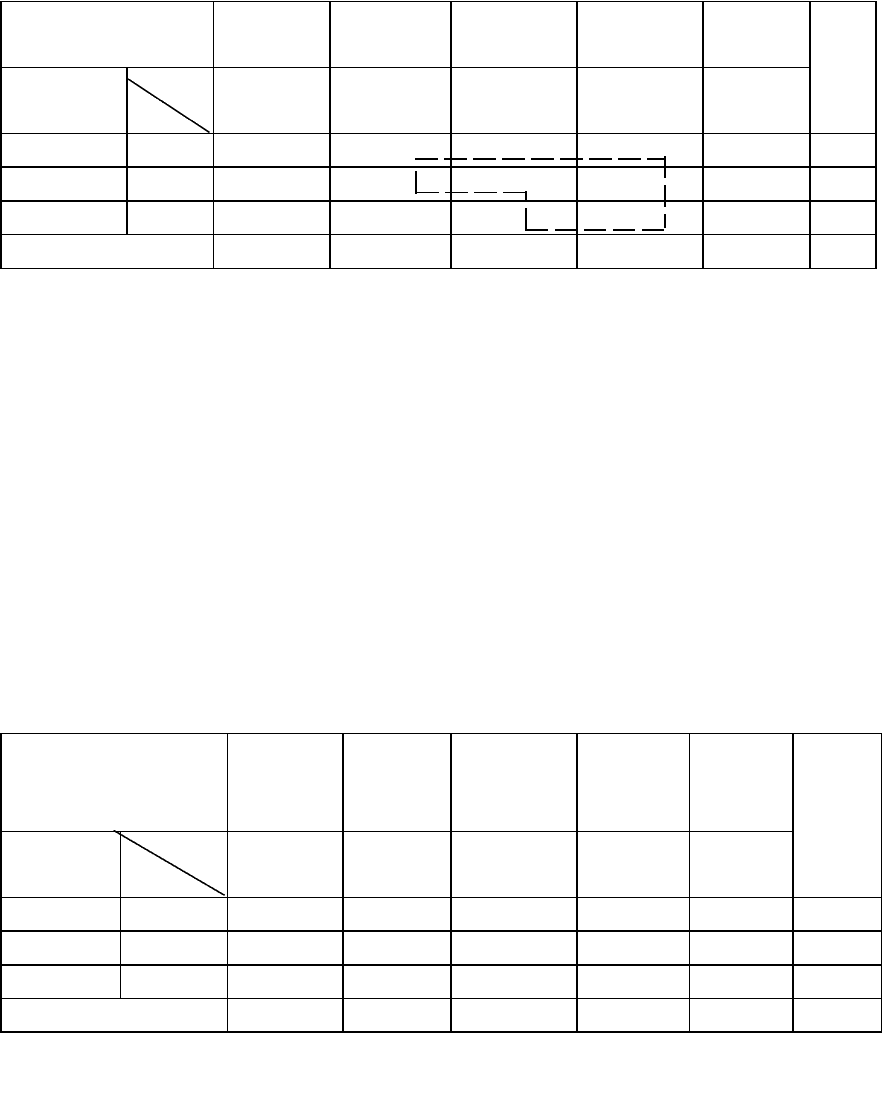
Матрица
планирования B
1
B
2
B
3
B
4
B
5
За-
Постав-
щики
v
j
u
i
v
1
=2
v
2
=3 v
3
=0 v
4
=2 v
5
=-3
пас
ы
A
1
u
1
=0 60
2
10 _
3 4
70 +
2 4
140
A
2
u
2
=1
8
60 +
4
120 _
1 14 1
180
A
3
u
3
=5
9
7
+
3
60 _
7
100
2
160
Потребности 60 70 120 130 100 480
Вновь строим систему потенциалов и проверяем выполнение
условия оптимальности для каждой незанятой клетки. Если получен
снова неоптимальный план, повторяем процесс до тех пор, пока не
будет выполняться условие оптимальности, т.е. возвращаемся на 2-й
этап.
Через конечное число таких шагов будет найдено оптимальное
решение транспортной задачи. Величина разности
0)(
ijji
cvu
в
незанятой клетке показывает, на сколько уменьшится стоимость плана
перевозок, если единицу груза перераспределить в эту клетку.
Новый план представлен в таблице 6.7. Полученный опорный план
удовлетворяет условиям оптимальности.
Таблица 6.7
Итоговая матрица планирования транспортной задачи
Матрица
планирования B
1
B
2
B
3
B
4
B
5
Запас
ы
Постав-
щики
v
j
u
i
v
1
=7
v
2
=6 v
3
=3 v
4
=7 v
5
=2
A
1
u
1
=-5 60
2 3 4
80
2 4
140
A
2
u
2
=-2
8
70
4
110
1 14 1
180
A
3
u
3
=0
9 7
10
3
50
7
100
2
160
Потребности 60 70 120 130 100 480
Значение функции
125021007503101110470280260 Z
(ст. ед.).
Решим с помощью метода потенциалов станковую задачу.
Пример 6.2. На предприятии имеется четыре группы станков,
каждый из которых может выполнять 5 видов элементарных операций
по обработке детали, причём операции могут производиться в любом
порядке. Максимальное время работы каждой из групп станков
91
1
2
3
5
4
6
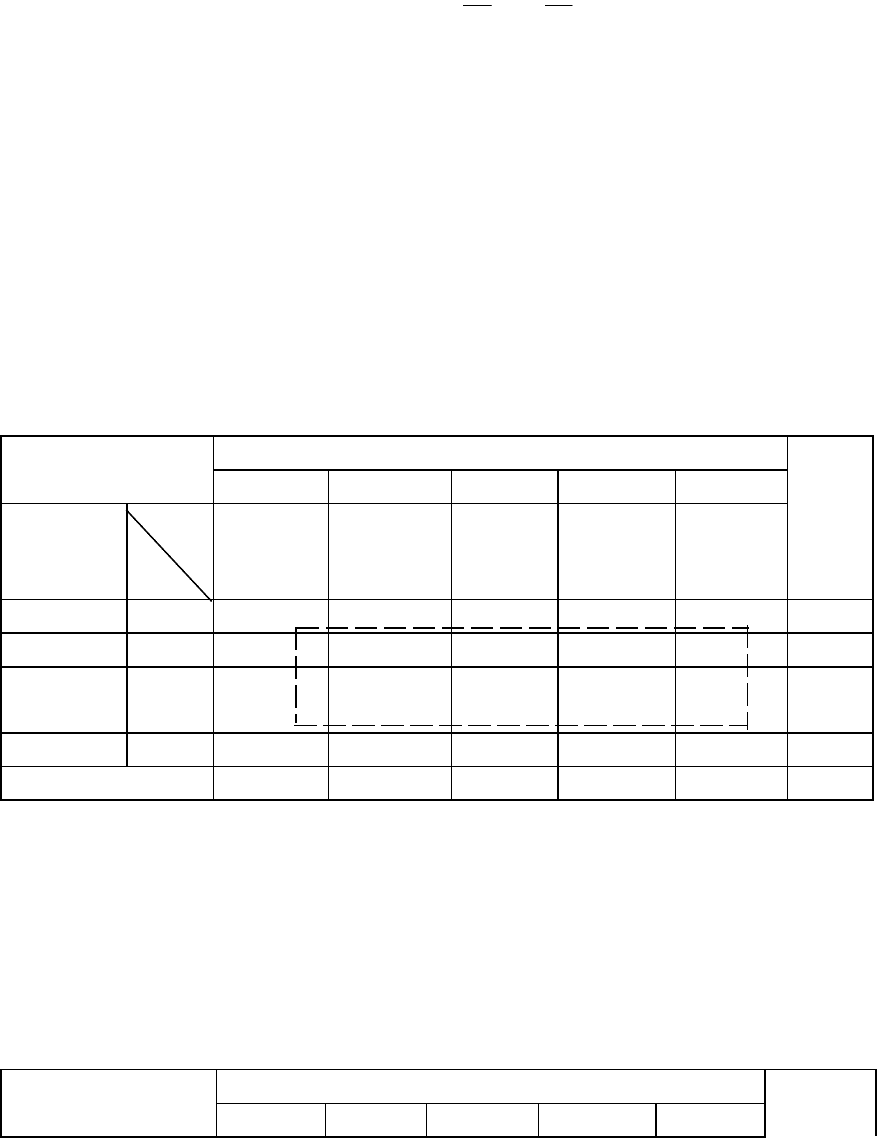
соответственно равно 320, 400, 240 и 400 ч; каждая операция должна
выполняться в течение 336, 224, 224, 288 и 288 ч.
Необходимо определить, сколько времени и на какой операции
нужно использовать каждую группу станков, чтобы обработать
максимальное количество деталей, если производительность каждого
станка группы известна и равна
)5,1;4,1( jiс
ij
.
.
34563
43452
25343
52634
C
Решение.
Чтобы преобразовать задачу на минимум, все
ij
c
берём со знаком
"-", составим первоначальный опорный план по наименьшим затратам
(табл. 6.8).
Таблица 6.8
Первый цикл алгоритма решения станковой задачи в виде транспортной
Матрица Потребители За-
планирования B
1
B
2
B
3
B
4
B
5
пасы
Постав-
щики
v
j
u
i
v
1
=0
v
2
=-3 v
3
=-3 v
4
=-2 v
5
=-2
a
i
A
1
u
1
=-3 +
-4 -3
224
-6 -2
96 _
-5
320
A
2
u
2
=-3 112
-3 -4 -3
288
-5 -2
400
A
3
u
3
=-2 48 _
-2 -5 -4 -3
192
-4
+
240
A
4
u
4
=-3 176
-3
224
-6 -5 -4 -3
400
b
j
336 224 224 288 288 1360
48
о
(единиц)
96,48min
. Осуществим перераспределение
поставок по циклу, состоящему из клеток (1,1), (1,5), (3,1), (3,5).
Получаем новый опорный план закрепления операций за станками. Он
является оптимальным (табл 6.9).
Таблица 6.9
Итоговая матрица планирования примера 6.2
Матрица Потребители
планирования B
1
B
2
B
3
B
4
B
5
Запа-
92
1
2
3
5
4
6

Постав-
щики
v
j
u
i
v
1
=0
v
2
=-3 v
3
=-2 v
4
=-2 v
5
=-1
сы
a
i
A
1
u
1
=-4 48
-4 -3
224
-6 -2
48
-5
320
A
2
u
2
=-3 112
-3 -4 -3
288
-5 -2
400
A
3
u
3
=-3
-2 -5 -4 -3
240
-4
240
A
4
u
4
=-3 176
-3
224
-6 -5 -4 -3
400
b
j
336 224 224 288 288 1360
Таким образом, для того чтобы обработать максимальное
количество деталей, необходимо, чтобы первая группа станков
выполняла первую операцию 48 ч, третью операцию 224 ч, пятую
операцию 48 ч, а вторая группа выполняла первую операцию 112 ч,
четвёртую 288 ч. и т. д. При этом будут обработаны: на первой
операции 1056 деталей
)31763112448(
, на второй операции 1344
деталей, на третьей операции 1344 деталей, на четвёртой 1440 деталей,
на пятой 1200 деталей, т.е. полностью можно обработать 1056 деталей.
Рассмотрим станковую задачу в другом виде.
Пример 6.3. Условия задачи.
На пяти токарных станках различных типов можно выполнять пять
операций по обработке деталей. При этом за каждым из станков может
быть закреплена лишь одна операция и одна и та же операция может
выполняться только одним станком. Зная время выполнения каждой из
операций на каждом из станков, которая задаётся матрицей, составить
такое распределение выполняемых операций между станками, при
котором суммарные затраты времени на обработку детали являются
минимальными.
54123
64319
85427
67231
38642
С
.
Эта задача аналогична задаче выбора (о назначениях).
Решение.
Составим математическую модель задачи. Обозначим через
)5,1;5,1( jix
ij
переменную, значение которой равно
1
, если на
i
-м
станке
j
-я операция выполняется, и равно 0 – в противном случае.
93
1
2
3
5
4
6

Тогда закрепление за каждым станком только одной операции
выражается равенствами:
,
,1
,1
1
,1
,1
5554535251
4544434241
3534333231
2524232221
1514131211
ххххх
ххххх
ххххх
ххххх
ххххх
а закрепление каждой из операций только на одном станке – равенствами:
.1
,1
,1
,1
,1
5545352515
5444342414
5343332313
5242322212
5141312111
ххххх
ххххх
ххххх
ххххх
ххххх
Требуется найти такие значения неизвестных
)5,1;5,1( jix
ij
,
удовлетворяющие системам линейных уравнений и равные 0 или 1, при
которых функция
F=2х
11
+4х
12
+6х
13
+8х
14
+3х
15
+х
21
+3х
22
+2х
23
+7х
24
+6х
25
+7х
31
+2х
32
+
+4х
33
+5х
34
+8х
35
+9х
41
+х
42
+3х
43
+4х
44
+6х
45
+3х
51
+2х
52
+х
53
+4х
54
+5х
55
принимает минимальное значение. Первоначальный опорный план
получим методом двойного предпочтения (табл.6.10).
Для построения системы потенциалов должно быть 9 занятых
клеток. У нас 5 единиц, введём в базис 4 нулевых клетки (по
возможности в клетки с наименьшей стоимостью). Полученный опорный
план оптимален.
S=
1513111111
=11.
Оптимальным планом является план, согласно которому на первом
станке выполняется пятая операция, на втором станке выполняется
первая операция, на третьем станке – четвёртая, на четвёртом станке –
вторая, на пятом станке – третья операция. Можно заметить, что клетка
(4,4) имеет нулевую оценку, т.е. если перераспределить третий станок за
второй операцией, а четвёртый за четвёртой операцией, то значение
S=11 не изменится, т.е. такой план также оптимален.
Таблица 6.10
Решение станковой задачи в виде задачи выбора (о назначениях)
Операции За
94
1
2
3
5
4
6

Станки
каждым
станком
закреп-
1 2 3 4 5 лена
Vj
Ui
v
1
=2 v
2
=3 v
3
=3 v
4
=6 v
5
=3 одна
операция
I u
1
=0 0
V
2 4 6 8
1
V
3
1
II u
2
=-1 1
V V
1 3
0
2 7 6
1
III u
3
=-1
7
0
V
2 4
1
5 8
1
IV u
4
=-2
9
1
V V
1 3
0
4
6
1
V u
5
=-2
3 2
1
V V
1
0
V
4 5
1
Каждая
операция
выполняется
только на
одном станке
1
1 1
1 1 5
Определение оптимального плана транспортных задач, имеющих
некоторые усложнения в их постановке
При нахождении решения ряда конкретных транспортных задач
часто бывает необходимо учитывать дополнительные ограничения,
которые не встречались выше при рассмотрении простых вариантов
данных задач. Остановимся подробнее на некоторых возможных
усложнениях в постановке транспортных задач и способах их решения.
1. При некоторых реальных условиях перевозки груза из
определённого пункта отправления
i
A
в пункт назначения
j
B
не могут
быть осуществлены (запрещены перевозки или блокирование
соответствующих клеток таблицы данных задачи). Для определения
оптимальных планов таких задач предполагают, что тариф перевозки
единицы груза из пункта
i
A
в пункт
j
B
является сколь угодно большой
величиной
M
, и при этом условии известными методами находят
решение новой транспортной задачи. При таком предположении
исключается возможность при оптимальном плане транспортной задачи
перевозить груз из
i
A
в
j
B
.
2. В отдельных транспортных задачах дополнительным условием
является обеспечение перевозки по соответствующим маршрутам
определённого количества груза. Пусть, например, из пункта
отправления
i
A
в пункт назначения
j
B
требуется обязательно перевезти
ij
d
единиц груза. Тогда в клетку таблицы данных транспортной задачи,
95
1
2
3
5
4
6

находящуюся на пересечении строки
i
A
и столбца
j
B
, записывают
указанное число
ij
d
и в дальнейшем эту клетку считают свободной со
сколь угодно большим тарифом перевозок
M
. Таким образом, для
получения новой транспортной задачи находят оптимальный план
(запасы и потребности делаются меньше на
ij
d
).
3. В некоторых транспортных задачах требуется найти
оптимальный план перевозок при условии, что из пункта отправления
i
A
в пункт назначения
j
B
перевозится не больше, чем
ij
единиц груза, т.е.
.
ijij
x
Сформулированную задачу можно решить так. В таблице исходных
данных задачи для каждого
j
-го ограничения предусматривают
дополнительный столбец, т.е. вводят дополнительный пункт
назначения. В данном столбце записывают те же тарифы, что и в
столбце
j
B
, за исключением тарифа, находящегося в
i
-й строке. Здесь
тариф равен
M
. При этом потребности
j
B
считают равными
ij
, а
потребности вновь введённого пункта назначения полагают равными
ijj
b
. Полученная транспортная задача решается методом
потенциалов, и будет найден оптимальный план или установлена
неразрешимость исходной задачи.
Вопросы для самопроверки
1. Область применения транспортных задач.
2. Классическая постановка транспортной задачи.
3. Открытая и закрытая модели транспортной задачи.
4. Теорема о разрешимости закрытой модели транспортной задачи.
5. Особенности транспортной задачи по сравнению с общей
задачей линейного программирования.
6. Станковая задача в форме транспортной.
7. Условия опорности первоначального плана транспортной задачи.
8. Метод северо-западного угла при нахождении опорного
первоначального плана транспортной задачи.
9. Метод минимальной стоимости при нахождении опорного
первоначального плана транспортной задачи.
10. Алгоритм метода потенциалов решения транспортных задач.
11. Определение оптимального плана транспортных задач,
имеющих некоторые усложнения в их постановке.
96
1
2
3
5
4
6

Тема 7 Нелинейное программирование
Как известно, общая задача математического программирования
формулируется следующим образом: найти вектор
),...,,(
21 n
xxxX
,
удовлетворяющий системе ограничений
),...,,(
21 ni
xxxg
b
i
, i=1,…,m,
(система иногда представляется через знак "=", но равенства всегда
можно переделать в неравенства) и доставляющий экстремум функции
),...,(
1 n
xxfZ
. При этом предполагается, что известны функции
),...,,(
21 ni
xxxg
и
),...,,(
21 n
xxxf
. Обычно на некоторые переменные из
набора
n
xxx ,...,,
21
накладывается условие неотрицательности. Если
miхaxxxg
n
j
jijni
,...,2,1,),...,,(
1
21
и
n
j
jjn
xcxxfZ
1
1
),...,(
, где
ij
a
и
j
c
– известные константы, то при условии неотрицательности решения
получаем задачу линейного программирования. Любую другую задачу
математического программирования, не удовлетворяющую таким
условиям, будем считать нелинейной.
Класс задач нелинейного программирования значительно шире
класса задач линейного программирования, поэтому в практике
экономико-математического моделирования необходимо знать и
применять методы нелинейного программирования. Основные
результаты в нелинейном программировании получены при
рассмотрении задач, в которых система ограничений линейная, а
целевая функция нелинейная. Даже в таких задачах оптимальное
решение может быть найдено только для узкого класса целевых
функций.
В евклидовом пространстве
n
E
система ограничений определяет
область допустимых решений задачи. В отличие от задач линейного
программирования она не всегда является выпуклой областью.
Если определена область допустимых решений, то нахождение
решения задачи нелинейного программирования сводится к
определению такой точки этой области, через которую проходит
гиперповерхность наивысшего (наинизшего) уровня
hxxxf
n
,,,
21
.
Указанная точка может находиться как на границе области допустимых
решений, так и внутри её, в отличие от задач линейного
программирования.
Процесс нахождения решения задачи нелинейного
программирования с использованием её геометрической интерпретации
включает следующие этапы:
97
1
2
3
5
4
6

1. Находят область допустимых решений задачи, определяемых
соотношениями
ii
bXg )(
(если она пуста, то задача не имеет решения).
2. Строят гиперповерхность
hхххf
n
),...,,(
21
.
3. Определяют гиперповерхность наивысшего (наинизшего)
уровня или устанавливают неразрешимость задачи из-за
неограниченности функции
),...,,(
21 n
хххf
сверху (снизу) на множестве
допустимых решений.
4. Находят точку области допустимых решений, через которую
проходит гиперповерхность наивысшего (наинизшего) уровня, и
определяют в ней значение функции
Xf
.
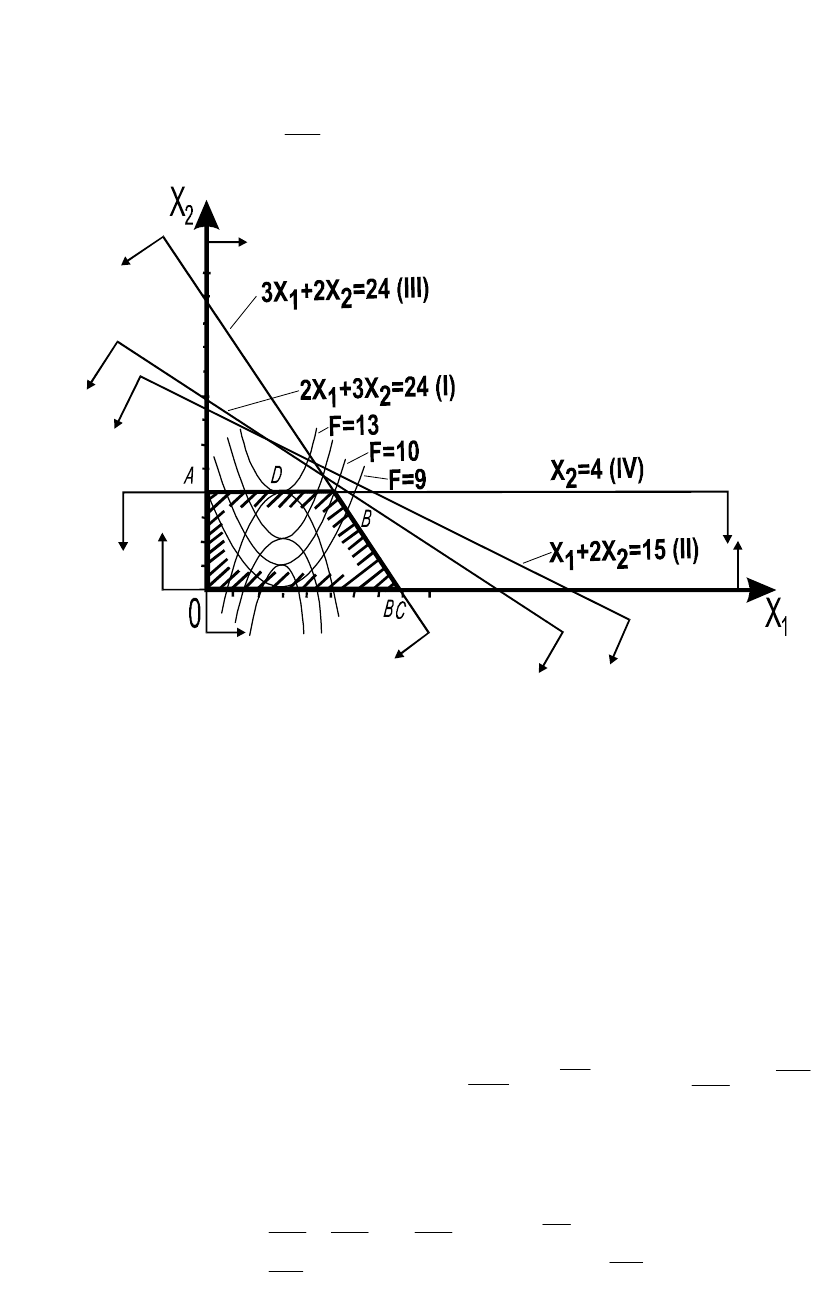
Пример 7.1. Найти максимальное значение функции
1
2
12
6xxxF
при условиях
.0,
,4
,2423
,152
,2432
21
2
21
21
21
xx
x
xx
xx
xx
Так как целевая функция нелинейная, то это задача нелинейного
программирования. Областью допустимых решений данной задачи
является многоугольник
OABC
. Следовательно, для нахождения её
решения нужно определить такую точку многоугольника
OABC
, в
которой функция
F
принимает максимальное значение.
Построим линию уровня
hxxxF
1
2
12
6
, где
h
– некоторая
постоянная, и исследуем её поведение при различных значениях
h
. При
каждом значении
h
получаем параболу, которая тем выше отдалена от
оси
1
OX
, чем больше значение
h
(рис. 7.1). Значит, функция
F
принимает максимальное значение в точке касания одной из парабол с
границей многоугольника
OABC
. В данном случае это точка
D
, в
которой гиперповерхность
136
1
2
12
xxxF
касается стороны
AB
многоугольника
OABC
. Координаты точки
D
можно найти из системы
уравнений:
.4
,136
2
1
2
12
x
xxx
Решив эту систему, получаем:
.4,3
*
2
*
1
xx
Итак,
13
max
F
при
).4;3(
*
x
Как видим, в задаче нелинейного программирования точка
максимального значения целевой функции не является в данном случае
вершиной многоугольника решений.
Рассмотрим частный случай общей задачи нелинейного
программирования, предполагая, что система ограничений содержит
98
1
2
3
5
4
6
только уравнения, отсутствуют условия отрицательности переменных и
),...,,(
21 n
xxxf
и
),...,,(
21 ni
xxxg
– функции, непрерывные вместе со
своими частными производными (по крайней мере, вторая частная
производная должна быть непрерывной.
max(min)),...,,(
21
n
xxxf
(7.1)
),1(),...,,(
21
mibxxxg
ini
(7.2)
1
2
1
5
4
1
8
3
1
2
Рис. 7.1. Геометрическое решение задачи
нелинейного программирования примера 7.1
В курсе математического анализа задачу (7.1)-(7.2) называют
задачей на условный экстремум или классической задачей
оптимизации. Чтобы вспомнить необходимые и достаточные условия
существования экстремума такой задачи, введём набор переменных
m
yyy ,,,
21
, называемых множителями Лагранжа, составим функцию
Лагранжа
m
i
niiinmn
,x,,xx-gbyxxxfyyyxxxL
1
212121,21
,,,,,,,,,
,
находим частные производные
nj
x
L
j
,1
и
,mi
y
L
i
1
и
рассматриваем систему
nm
уравнений (здесь привлечём необходимое
условие экстремума, заключающееся в том, что первая производная
должна быть равна
0
):
),1(;0),...,,(
),1(;0
21
1
mixxxgb
y
L
nj
x
g
x
L
x
L
nii
i
m
j
i
jj
i
(7.3)
99
1
2
3
5
4
6

с
nm
неизвестными
mn
yyyxxx ,...,,,,...,,
2121
. Всякое решение системы
уравнений (7.3) определяет точку
),...,,(
**
2
*
1
*
n
xxxX
, в которой может
иметь место экстремум функции
),...,,(
21 n
xxxf
. Следовательно, решив
систему (7.3), получают все точки, в которых функция
),...,,(
21 n
xxxf
может иметь экстремальные значения. Дальнейшее исследование
найденных точек проводят так же, как и в случае безусловного
экстремума (здесь привлекается достаточное условие экстремума – если
вторая производная меньше нуля, то имеет место максимум, если
больше нуля – минимум).
Таким образом, определение экстремальных точек задачи
нелинейного программирования (7.1)-(7.2) методом множителей
Лагранжа включает следующие этапы:
1. Составляют функцию Лагранжа.
2. Находят частные производные от функции Лагранжа по
переменным
j
x
и
i
y
и приравнивают их 0.
3. Решая систему уравнений (7.3), находят точки, в которых
целевая функция может иметь экстремум.
4. Среди точек, подозрительных на экстремум, находят точки, в
которых достигается экстремум, и вычисляют значения целевой
функции в этих точках.
Рассмотрим пример.
Пример 7.2.
Предприятию необходимо изготовить 180 деталей. Эти изделия
могут быть изготовлены двумя технологическими способами. При
производстве
1
x
изделий I способом затраты равны
2
11
4 xx
(руб.), а при
изготовлении
2
x
изделий II способом они составляют
2
22
8 xx
(руб.).
Определить, сколько изделий каждым из способов следует изготовить
так, чтобы общие затраты на производство продукции были
минимальными.
Решение.
Математическая модель задачи нелинейного программирования
состоит в следующем: найти минимум функции
2
22
2
11
84 xxxxf
при
условиях
180
21
xx
и
0,
21
хх
.
Решим задачу, используя метод множителей Лагранжа. Найдём
минимальное значение функции при условии
180
21
xx
, т.е. без учёта
требования неотрицательности переменных. Для этого составим
функцию Лагранжа
)180(84,,
21
2
22
2
1121
xxyxxxxyxxF
.
Вычислим её частные производные по
1
x
,
2
x
,
y
и приравняем их
0
:
100
1
2
3
5
4
6
