Маслов А.В., Григорьева А.А. Математическое моделирование в экономике и управлении: Учебное пособие. Гриф УМО
Подождите немного. Документ загружается.


.0180
,028
,024
21
2
2
1
1
xx
F
yx
x
F
yx
x
F
Перенесём в правые части первых двух уравнений
y
и,
приравнивая их левые части, получим
21
2824 xx
или
2
21
xx
.
.180
,2
21
21
xx
xx
.89 ,91
*
2
*
1
xx
Решаем совместно систему, т.е. получаем координаты точки,
удовлетворяющие условиям неотрицательности. Эта точка является
подозрительной на экстремум. Используя вторые частные производные,
выясняем, что в этой точке функция
f
имеет условный минимум. То же
получим, если исследование на условный экстремум функции
f
сведём
к исследованию на безусловный экстремум функции
1
f
, полученной из
f
в результате её преобразований: из уравнения связи найдем
12
180 xx
и подставим в целевую функцию, получим функцию одной
переменной
1
x
:
2
11
2
111
18018084 xxxxf
.
;03644
1
1
x
x
f
;
91
1
x
;
89
2
x
;
04
2
1
2
dx
fd
, т.е. в этой точке имеем
минимум.
Метод множителей Лагранжа можно применять и в том случае,
когда условия связи представляют собой неравенства.
Так, если требуется найти экстремум функции
)(xfz
при условии
bxg )(
, то сначала следует найти точки безусловного экстремума
функции
xfz
из уравнений
0
k
x
f
nk ,1
, затем среди этих точек
отобрать те, координаты которых удовлетворяют условию связи
bxg
, и, наконец, определить точки, удовлетворяющие системе уравнений:
bxg
nk
x
g
y
x
f
kk
)(
),1(,0
.
Tочки, найденные в результате решения этой системы, вместе с
точками, определёнными на первом этапе и удовлетворяющими
условию
bxg
, подлежат дальнейшему исследованию, как и при
нахождении безусловного экстремума.
В заключение рассмотрения метода Лагранжа для решения задач
нелинейного программирования скажем, что функцию Лагранжа можно
трактовать и в определённом экономическом смысле. Если
максимизируемую функцию интерпретировать как прибыль, а правые
части неравенств
ii
bxg )(
как величину отпущенных ресурсов, то
множитель y можно рассматривать как стоимость единицы ресурсов.
Тогда
),...,(
2,1 nii
xxxgby
определит экономию ресурсов в денежном
101
1
2
3
5
4
6
выражении, а функция Лагранжа
yxxxfL
n
),...,(
21
),...,,(
21 n
xxxgb
будет являться величиной общего дохода.
Для общей задачи нелинейного программирования
max(min)),...,,(
21
n
xxxf
(7.4)
),1(),...,,(
21
mibxxxg
ini
(7.5)
),1(0 njx
j
(7.6)
Как уже упоминалось, для отдельных классов задач, в которых
сделаны дополнительные ограничения относительно свойств функции
f
и
i
g
разработаны эффективные методы их решения. В частности, ряд
таких методов имеется для решения задач нелинейного
программирования (7.4)–(7.6) при условии, что
f
– вогнутая
(выпуклая) функция и область допустимых решений, определяемая
ограничениями (7.5)–(7.6), – выпуклая.
Определение 7.1.
Функция
),...,,(
21 n
xxxf
, заданная на выпуклом множестве X,
называется выпуклой, если для любых двух точек
1
x
и
2
x
из X и
любого
10
выполняется соотношение
)()1()()1(
1212
xfxfxxf
.
102
1
2
3
5
4
6

Определение 7.2.
Функция
),...,,(
21 n
xxxf
, заданная на выпуклом множестве X,
называется вогнутой, если для любых двух точек
1
x
и
2
x
из X и любого
10
выполняется соотношение
)()1()()1(
1212
xfxfxxf
.
Определение 7.3.
Говорят, что множество допустимых решений задачи (7.4)–(7.6)
удовлетворяет условию регулярности, если существует, по крайней
мере, одна точка
i
x
, принадлежащая области допустимых решений,
такая, что
),1()( mibxg
iii
.
Определение 7.4.
Задача (7.4)–(7.6) называется задачей выпуклого
программирования, если функция
n
xxxf ,,,
21
является вогнутой
(выпуклой), а функции
),1)(( mixg
i
– выпуклыми.
Теорема 7.1.
Любой локальный максимум (минимум) задачи выпуклого
программирования является глобальным максимумом (минимумом).
Что называется функцией Лагранжа, уже было пояснено, седловой
же точкой функции Лагранжа называется точка
),,...,,;,...,,();(
00
2
0
1
00
2
0
100 mn
yyyxxxYX
если
),...,,,,...,,(
,...,,,,...,,,...,,,,...,,
21
00
2
0
1
00
2
0
1
00
2
0
1
00
2
0
121
mn
mnmn
yyyxxxL
yyyxxxLyyyxxxL
для всех
),1(0 njx
j
и
),1(0 miy
i
.
Теорема Куна – Таккера
Теорема 7.2. Для задачи выпуклого программирования (7.4)–(7.6),
множество допустимых решений которой обладает свойством
регулярности, план
),...,,(
00
2
0
10 n
xxxX
является оптимальным планом
тогда и только тогда, когда существует такой вектор
),1,0( ),...,,(
000
2
0
10
miyyyyY
im
, что
00
;YX
– седловая точка функции
Лагранжа.
Если предположить, что целевая функция
F
и функции
i
g
непрерывны и дифференцируемы, то теорема Куна-Таккера может быть
дополнена аналитическими выражениями, определяющими
необходимое и достаточное условие того, чтобы точка
00
;YX
была
седловой точкой функции Лагранжа, т.е. являлась решением задачи
выпуклого программирования. Эти выражения имеют следующий вид:
),1(0
),1(0
),1(0
),1(0
),1(0
),1(0
0
0
0
00
0
miy
mi
y
L
y
mi
y
L
njx
nj
x
L
x
nj
x
L
i
i
i
i
j
j
j
j
103
1
2
3
5
4
6
где
j
x
L
0
и
i
y
L
0
– значения соответствующих частных производных
функции Лагранжа, вычисленных в седловой точке.
Теорема Куна-Таккера в теории нелинейного программирования
занимает центральное место. Она справедлива и для задач так
называемого квадратичного программирования, т.е. где целевая
функция
n
i
n
k
n
j
jkkjjj
xxcxdxF
1 1 1
)(
при ограничениях:
n
j
jijij
njxmibxa
1
),1(0);,1(
.
В общем случае решения задач нелинейного программирования для
определения глобального экстремума задачи не существует
эффективного вычислительного метода, если неизвестно, что любой
локальный экстремум одновременно является и глобальным. Так, в
задаче выпуклого и квадратичного программирования множество
допустимых решений выпукло, то, если целевая функция вогнута,
любой локальный максимум является также и глобальным.
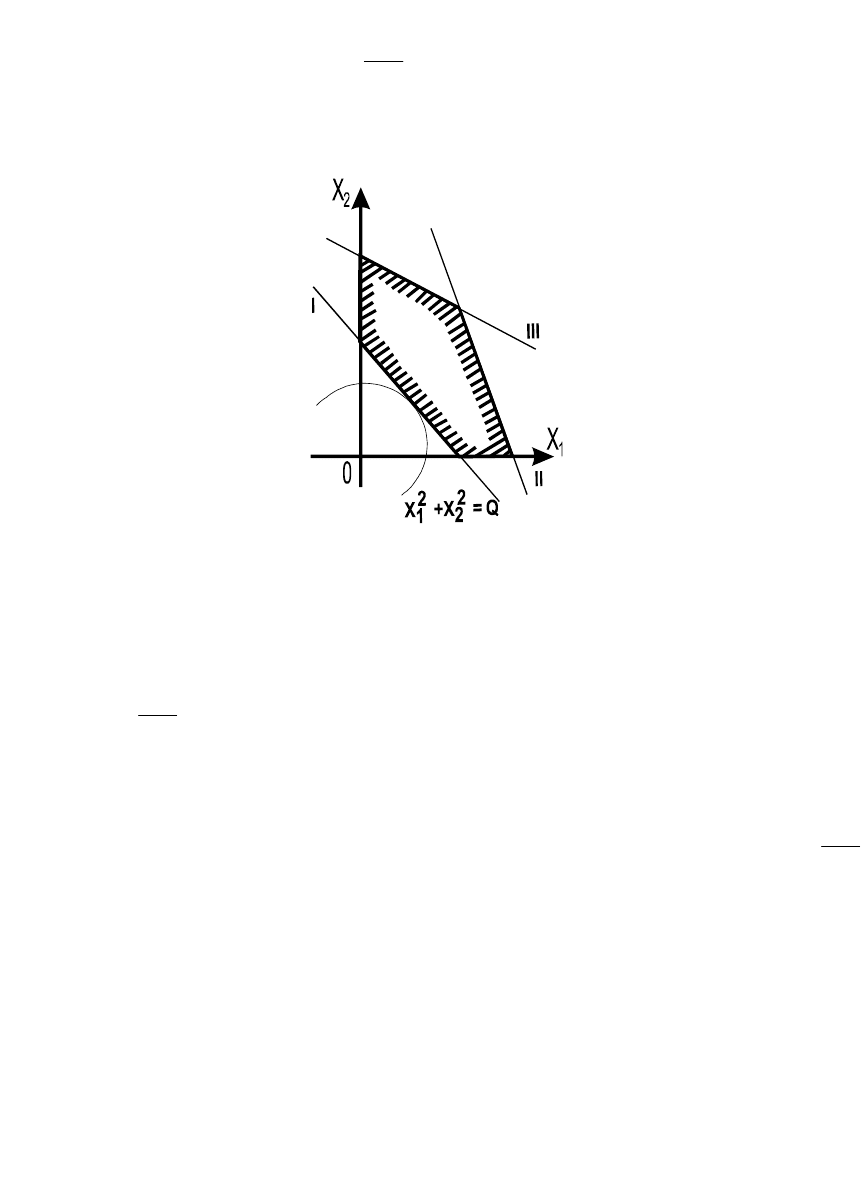
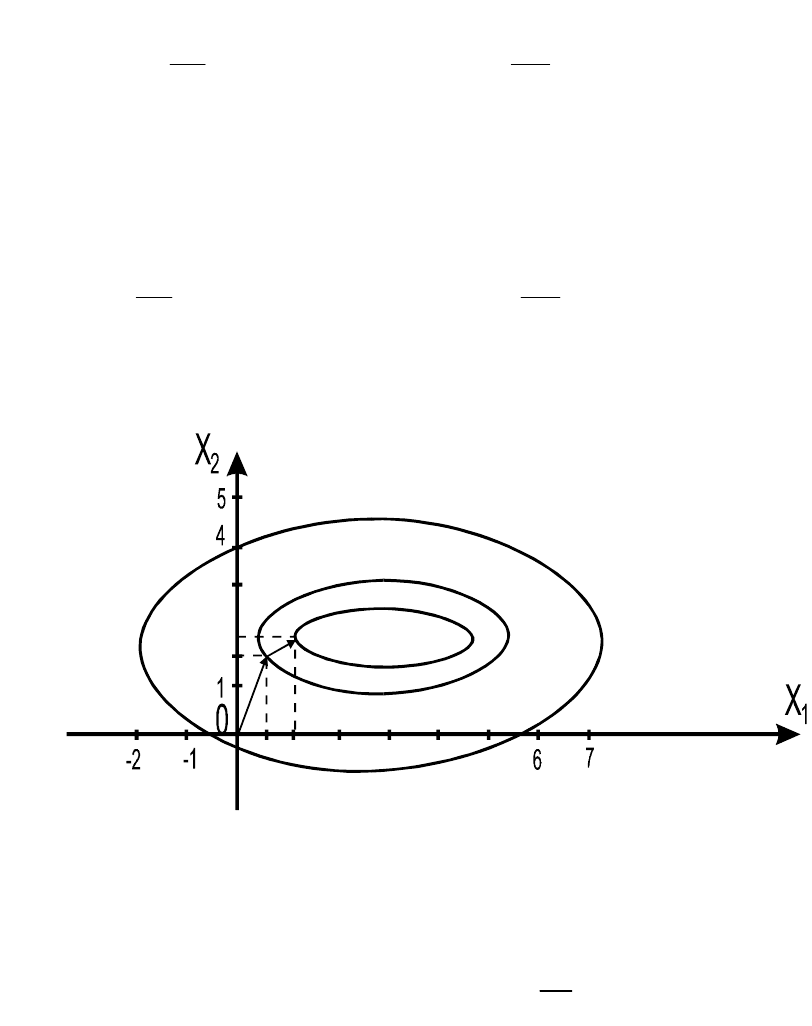
Пример 7.3. С помощью теоремы Куна-Таккера найдём
2
2
2
1
max xxZ
при ограничениях
.0,0
,6
,82
,22
21
21
21
21
xx
xx
xx
xx
Решаем графически (рис. 7.2) и находим:
8,0
1
x
;
4,0
2
x
;
8,0Z
(более подробно решение см. ниже). Покажем, что существует вектор
Y
0
0, при котором в точке оптимума выполняются условия Куна-
Таккера. Составим функцию Лагранжа:
)6()28()22(),(
213212211
2
2
2
1
xxyxxyxxyxxYXL
.
Находим:
02
0222
3212
2
3211
1
yyyx
x
L
yyyx
x
L
028
022
21
2
21
1
xx
y
L
xx
y
L
0)22(
06
0)2(
0)222(
211
1
1
21
3
32122
2
2
32111
1
1
xxy
y
L
y
xx
y
L
yyyxx
x
L
x
yyyxx
x
L
x
.0,,,,
0)6(
0)28(
32121
213
3
3
212
2
2
yyyxx
xxy
y
L
y
xxy
y
L
y
Решение
4,0;8,0
21
xx
находим из системы:
22
21
2
2
2
1
xx
Qxx
. Из
второго уравнения
12
22 xx
подставляем в первое уравнение системы.
Дифференцируем по
1
x
:
0810
1
x
. В выражения
2
y
L
и
3
y
L
подставляем значения
8,0
1
x
и
4,0
2
x
. Имеем значения частных
104
1
2
3
5
4
6
производных больше нуля, а по условию должны быть равно нулю,
тогда
2
y
=0 и
3
y
=0. С другой стороны,
1
y
может принимать
ненулевые значения, т.к.
,0
1
1
y
L
y
отсюда
8,0
1
y
; все
,0
i
y
т.е.
условия Куна-Таккера выполняются, следовательно, эта точка – точка
экстремума.
Рис.7.2. Графическое решение задачи нелинейного
программирования примера 7.3
Необходимое условие оптимальности для задачи нелинейного
программирования можно сформулировать следующим образом. Пусть
0
M
– оптимальное решение задачи (7.4)–(7.6), причём функции
0
MF
,
0
Mg
i
,
mi ,1
дифференцируемы в этой точке. Если
0
M
– неособая
точка допустимого множества задачи (7.4)–(7.6), то она является точкой
Куна-Таккера этой задачи.
Таким образом, если допустимое множество
задачи (7.4)-(7.6)
не имеет особых точек, а функции F(М), g
i
(М), (
mi ,1
)
дифференцируемы во всех точках
, то оптимальное решение этой
задачи следует искать среди точек Куна-Таккера.
Как известно из математического анализа, особой точкой
множества допустимых решений системы линейных уравнений и неравенств
вида
lkiМФkiМФ
ii
,...,1,0)( ,,...,1;0)(
,
т. е. множества допустимых решений
,,...,1,0)(;,...,1,0)(( lkiМФkiМФRМV
ii
n
если в точке
0
M
линейно зависимы градиенты тех функций
)(МФ
i
,
которые в ней обращаются в
0
. Например,
0,0,2
0
M
– особая точка
множества
105
1
2
3
5
4
6

.
02)(
,04)(
),,(
1
2
2
2
12
2
3
2
2
2
11
3
321
xxxМФ
xxxМФ
RxxxМV
Действительно,
).0;0;2();0;0;4()(,0)(,0)(
00
21020
ММi
gradФФgradМФМФ
Таким образом,
00
21
2
ММ
gradФgradФ
– линейно зависимая система.
Градиент функции
)(),...,(),(
00
2
0
1
0
М
x
f
М
x
f
М
x
f
f
n
М
– это
вектор, координаты которого соответственно равны значениям частных
производных функции
Mf
в точке M
0
. Этот вектор показывает
направление быстрейшего роста функции.
Необходимое условие оптимальности малопригодно для решения
большинства задач нелинейного программирования, т.к. лишь в редких
случаях удается найти все точки Куна-Таккера задачи нелинейного
программирования.
Достаточное условие оптимальности для задачи нелинейного
программирования: если
00
;YX
– седловая точка функции Лагранжа
для задачи (7.4)–(7.6), то
0
X
является оптимальным решением этой задачи.
Это условие в общем случае не является необходимым: функция
Лагранжа может не иметь седловых точек, в то же время исходная
задача нелинейного программирования обладает оптимальным
решением.
Известны различные методы, позволяющие найти оптимальное
решение задачи нелинейного программирования приближённо. Однако
эти методы дают достаточно хорошее приближение лишь для задачи
выпуклого программирования, где всякий локальный экстремум
является одновременно и глобальным. В общем случае под
градиентными методами понимают методы, в которых движение к
точке оптимума функции совпадает с направлением градиента этой
функции, т.е. начиная с некоторой точки
k
x
осуществляется
последовательный переход к некоторым другим точкам до тех пор, пока
не выявится приемлемое решение исходной задачи. При этом
градиентные методы могут быть подразделены на 2 группы.
К первой группе относятся методы, при использовании которых
исследуемые точки не выходят за пределы области допустимых
решений задачи. Наиболее распространенным из таких методов
является метод Франка-Вольфа (Вулфа). К числу таких методов
относится метод проектируемых градиентов Розена, метод
допустимых направлений Зойтендейка.
106
1
2
3
5
4
6
Ко второй группе относятся методы, при использовании которых
исследуемые точки могут как принадлежать, так и не принадлежать
области допустимых решений. Однако в результате реализации
итерационного процесса находится точка области допустимых решений,
определяющая приемлемое решение.
Из таких методов наиболее часто используется метод штрафных
функций или метод Эрроу-Гурвица.
При нахождении решения задач градиентными методами, в том
числе и названными, итерационный процесс осуществляется до того
момента, пока градиент функции
),...,,(
21 n
xxxf
в очередной точке
)1( k
x
не станет равным нулю или же пока
)()(
)1( kk
xfxf
, где
–
достаточно малое положительное число, характеризующее точность
полученного решения.
Решение сложных задач нелинейного программирования
градиентными методами связано с большим объёмом вычислений и
целесообразно только с использованием ЭВМ.
На примере покажем общий смысл градиентных методов решения
задач нелинейного программирования.
Пусть имеется функция двух переменных
),(
21
xxfz
. Пусть
исходные значения переменных будут
0
2
0
1
, xx
, а значение функции
),(
0
2
0
1
xxf
. Если
),(
0
2
0
1
0
xxfz
не является экстремумом, то определяют
такие новые значения переменных
1
0
1
'
1
dxx
и
2
0
2
'
2
dxx
, чтобы
следующее значение функции
'
2
'
1
, xxf
оказалось ближе к оптимуму,
чем предыдущее.
Каким же образом определяется величина приращений
1
d
и
2
d
?
Для этого в точках
0
1
x
и
0
2
x
определяется направление изменения
функции в сторону экстремума с помощью градиента. Чем больше
значение частной производной, тем быстрее происходит изменение
функции в сторону экстремума. Поэтому приращения
1
d
и
2
d
выбирают пропорциональными значению частных производных
1
x
z
и
2
x
z
в точках
0
11
xx
и
0
22
xx
. Таким образом,
1
1
x
z
td
и
2
2
x
z
td
, где
t
– величина, называемая шагом, которая устанавливает масштаб изменений
1
d
и
2
d
.
Пример 7.4.
Пусть необходимо максимизировать функцию
2
2
2
1
)2(4)3( xxZ
(максимум в точке (3;2))
);3(2
1
1
x
x
Z
28
2
2
x
x
Z
.
107
1
2
3
5
4
6
В точке
0
0
1
x
,
0
0
2
x
при
1,0t
имеем
6,03021,0
1
0
1
x
Z
td
;
6,12081,0
2
0
2
x
Z
td
,
откуда
6,06,00
0
1
0
1
1
1
dxx
;
6,16,10
0
2
0
2
1
2
dxx
;
4,6)26,1(4)36,0(
22
Z
.
Проведём ещё одну итерацию. В точке
6,0
1
1
x
,
6,1
1
2
x
при
1,0t
имеем
48,036,021,0
1
1
1
x
Z
td
;
32,026,181,0
2
1
2
x
Z
td
,
откуда
08,148,06,0
1
1
1
1
2
1
dxx
;
92,132,06,1
1
2
1
2
2
2
dxx
;
712,3)292,1(4)308,1(
222
Z
.
Рис.7.3. Геометрическая интерпретация двух шагов
градиентного метода для примера 7.4
На рис. 7.3 показано движение по градиенту, которое было
проведено в данном примере. Отношение
1
2
d
d
указывает направление
изменения функции в сторону максимума. Если градиент взять со
знаком минус, то будем двигаться в сторону минимума.
Специфической проблемой градиентных методов является выбор
величины шага t. Если задаться малым шагом, то оптимум будем искать
очень долго. Если выбрать его значение слишком большим, то оптимум
можно "проскочить". Соответствующими методами решается
промежуточная задача выбора оптимальной величины шага. Если шаг t
определяется приближённо, то, как правило, попадают не в оптимум, а в
его зону. Градиентные методы обеспечивают определение локальных
X
1
1
=
0,6
X
2
=1,08
X
2
2
=1,92
X
1
2
=
1,6
108
1
2
3
5
4
6
оптимумов. При отыскании глобального оптимума с помощью
градиента нередко бывает сомнение в том, что найденный оптимум
является глобальным. В этом недостаток этого метода при решении
задач невыпуклого программирования.
Вопросы для самопроверки
Постановка задачи нелинейного программирования.
Процесс нахождения решения задачи нелинейного
программирования с использованием её геометрической
интерпретации.
Алгоритм метода Лагранжа решения задачи нелинейного
программирования.
Применение метода Лагранжа к решению задачи нелинейного
программирования в случае, когда условия связи представляют
собой неравенства.
Вспомогательные определения и теоремы, необходимые для
рассмотрения центральной теоремы нелинейного
программирования – теоремы Куна-Таккера.
Теорема Куна-Таккера.
Необходимое и достаточное условие оптимальности для задачи
нелинейного программирования.
Общий смысл градиентных методов приближённого решения задач
нелинейного программирования.
Группы градиентных методов приближённого решения задач
нелинейного программирования.
Тема 8 Регрессионный анализ
Эта тема тесно связана с курсом общей теории статистики и во
многом опирается на понятия и определения, данные в этом курсе,
особенно с разделом "Статистическое изучение связи между
признаками".
Регрессионный анализ – раздел математической статистики,
объединяющий практические методы исследования регрессионной
109
1
2
3
5
4
6

зависимости между величинами по данным статистических
наблюдений. Регрессия – зависимость среднего значения какой-либо
случайной величины от некоторой другой величины или нескольких
величин. Смысл регрессионного анализа состоит в выводе уравнения
регрессии (включая оценку его параметров), с помощью которого
оценивается величина случайной переменной, если величина другой
(или других в случае множественной или многофакторной регрессии)
известна, т.е. фиксирована, неслучайна.
В отличие от этого корреляционный анализ применяется для
нахождения и выражения тесноты связи между случайными
величинами, хотя часто эти методы объединяют в корреляционный
анализ.
Практически речь идёт о том, чтобы, анализируя множество точек
на графике (т.е. множество статистических данных), найти линию, по
возможности точно отражающую заключённую в этом множестве
закономерность, тенденцию – линию регрессии.
Существует ряд математико-статистических приёмов,
позволяющих решить эту задачу. В случае, когда искомая
закономерность может быть принята за линейную, наиболее эффективен
метод наименьших квадратов.
Регрессионный анализ применяется в различного рода
экономических исследованиях (производственные функции, анализ
эластичности спроса от цены и др.), особенно при анализе
хозяйственной деятельности предприятий (для определения влияния
отдельных факторов на результаты) и во многих других областях
экономической науки и хозяйственной практики.
Пример: средняя себестоимость поковок в кузнечных цехах
машиностроительных заводов, по статистическим исследованиям,
описывается следующим уравнением регрессии:
321
834,0682,0605,08,72 xxxy
, где
1
x
– заработная плата на 1 т
поковок,
2
x
– удельная металлоёмкость,
3
x
– удельные цеховые
расходы. Это уравнение означает, что лишний расход одного рубля
заработной платы приведёт (приблизительно, в среднем) к повышению
средней себестоимости тонны поковок на
605,0
руб. Соответственно
рассчитывается и влияние 2-х остальных факторов.
Таким образом, регрессионный анализ является методом
статистической обработки наблюдений, в результате которой
оказывается возможным составить уравнение регрессии и получить
количественную оценку влияния факторных признаков на
результативный признак.
110
1
2
3
5
4
6
