Машимов М.М. Геодезия.Теоретическая геодезия
Подождите немного. Документ загружается.


Таблица 10
V»
А„
Vс
VI ОХ— 1>(Х
Дг
Дф
\\ V
1 0
<ЭФ„
д{
дФ
а
дб
— 1
0
ЗФ„
Зф
ЗФ„
д1
1 0
0
дФ
г
дФг
0
дФ
г
дФ
г
0 0
д1
дб
0
Зф д1
0
Система уравнений поправок (438) и ее решение в матричных сим-
волах имеет вид
АУ
0
+ ВХа+ХР
0
=0; Уо= -яА'Р
0
(ВХ
0
+ Г
0
);
Ро
= (АдА')~
[
-, Х0=-{В'Р
0
В)~
{
В'Р^0. (439)
Весовая матрица Ро — квазидиагональная и состоит из квадратных
матриц второго порядка для каждого светила. Заметим, что применение
нестрогих формул (436) и (437) искусственно разделяет совместные
измерения на две самостоятельные группы, которые могут быть обрабо-
таны раздельно при условии У'рУ— тт и У'рУ — тт, поскольку обрат-
ные веса связующих поправок (к
5
—
г>
а
) и Vв приняты равными нулю.
Конечно, применение нестрогих формул (436) и (437) несколько упро-
щает вычисления, однако такое упрощение допустимо только для обра-
ботки измерений невысокой точности.
4.16. УРАВНЕНИЕ РАДИУСА ЗЕМНОГО ЭЛЛИПСОИДА
4.16.1. Уравнение радиуса трехосного эллипсоида
Рассмотрим трехосный эллипсоид с полуосями а>а-\/1
—
е
2
>
>аУ
1
—ё
г
(е, е — соответственно эксцентриситеты экваториального
и меридионального эллипсов). Уравнение такого эллипсоида
(х
2
+ у
2
)/(
1
-
е
2
)
+ г
2
/(
1
- е
2
) = а
2
. (439)
Из этого уравнения получим планетоцентрический радиус
г = а\
1
- е
2
)
(1
- е
2
) + е\х
2
+ у
2
) + е
2
(х
2
+ г
2
) - е
2
г
2
х
2
. (440)
Если обозначить через А,о долготу меридиана большой полуоси а трех-
осного эллипсоида, то
х~гсозфсоз(Х—
Ко)',
у—гсо5ц>а'т(к —
ко)',
г=/
-
зтф. (441)
Подставив значения декартовых координат (441) в выражение (440)
и выполнив несложные преобразования, получим формулы
г = а
л
/Т^е
Г
/
л
/Т+^
2
5\г^^^о^соз
2
^^ (442)
150

V»
= («.»-,/•)/( 1-е"). (443)
представляющие плаиетоцеитрический радиус трехосного эллипсоида
относительно его параметров а, е, е, Яо и сферические координаты
<р и Я.
Правую часть формулы (442) разложим в ряд по степеням малого
параметра у
2
зт
2
ф
—
е
2
С05
2
фС05(Я,—
ко)
и, пользуясь соотношениями
2соз
2
Я
= соз
2Я
+ 1;
8соз
4
к = соз
4Я
+ 4 соз 2Я + 3; (444)
32 соз
6
Я,
= соз 6Я + 6 соз 4 к + 15 соз 2к + 10,
запишем следующее выражение
г = а^\— е
2
[(1 —^г
2
5т
2
ф + -|-у
4
8т
4
ф—[|-г
6
зт
6
ф + -||р>
8
зт
8
ф +
. I О 2 3 9 0.0 2.9А 4 , 15 42.4 2
+—е соз ф——V е зт фсоз ф + —е соз ф + —V е зт фсоз ф
—
4 о 04 О л,
45 2 4 * 2 4 I 25 й й 35 6 2-6 2 »
"""128*'
у е 8|П
Ф
со8
^ 256
6 005
У°е 81!ГфС05ф +
. 315 44.4 4 \ I / 1 9 2 З99.9 2 ,
+ -^уу е зт фсоз ф I + ( -^-е соз ф ——^е зт фсоз ф +
I 3 4 4 , 15 4 9 • 4 2 1524*2 4 1 75 А А
Н——8 СОЗ ф + — V 8 31П ф
СОЗ
ф 32^
е
5'
п
ф
СОЗ
ф Н—р^е СОЗ ф —
—|г
л
'
6е2 5
'
п6
45
0082
^ ^—Г^
Л
'
4е4 5
'
п4
Ф
С054
Ф
)
С05
2(Я—Яю)
+ ^ -^-е
4
соз
4
ф —
15 2 4 . 2 4 , 15
128
24*2 4 , 15
6
я .105 44.4 4 \ . ,
V е зт ф соз ф + "25§"
е 005
Ф "5ЙГ
5,п
Ф
005
Ф ] X
X соз4(Я —Я
0
)+-^у2-е
6
соз
6
фСОз6(Х —Яо)].
Тригонометрические функции можно заменить сферическими функ-
циями
5т
2
ф=-^-+-|-/>2(ц); З1П
4
ф=4-+Т
/
'
2(
^+А
Р4(
^
;
• 8 1 , 40 о , . , 48 п ... 64 о , . . 128 „ , .
зт
8
Ф
=
Т
+ддЛ(ц) +-^3 РМ + + 6435 ^в(ц);
соз
2
ф=-Ря( р); соз
4
ф=РЖ р.) Р
4
( р);
8
128 512
0
, . . 2304 „ , , 512 „ . . . 128 _ . .
С05
^Цб™Йз'^'
151
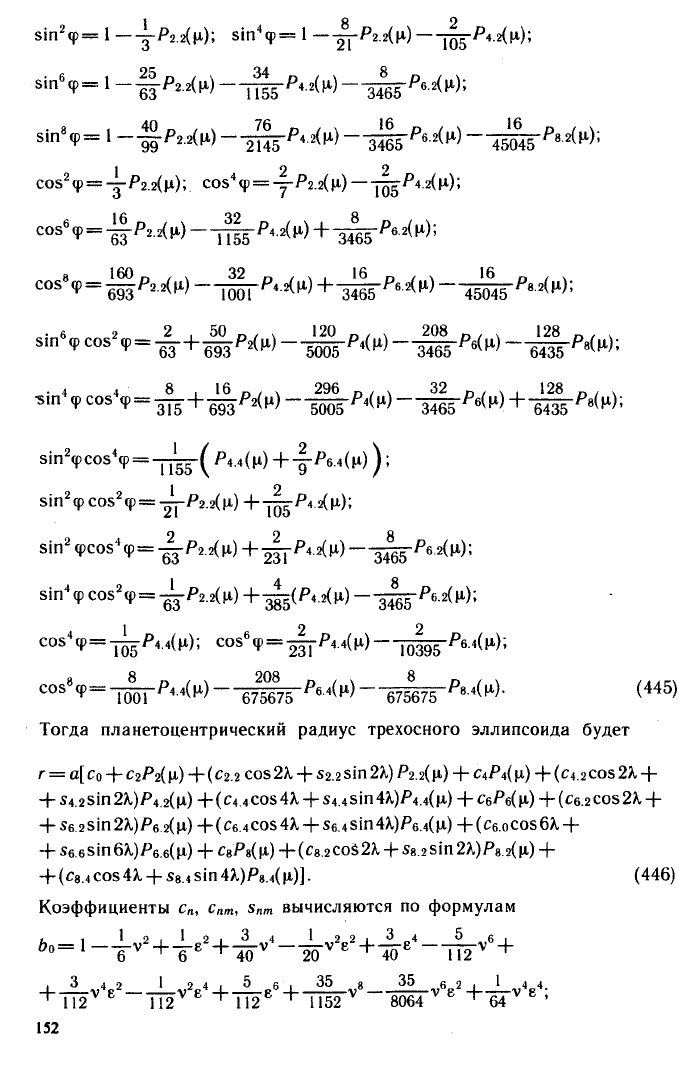
1 8 2
51П
2
ф=
1
д-Рг.гМ; зт
4
ф =
1
—-^у-Рг.гМ ^Р
42
<ц);
зт
8
ф=
1
-^РМ- ^-Р^-^Р^—^-Р^)-
1 2 2
соз
2
ф="з"Р2.2( ц); соз
4
ф=—Р
2
.2( ц)—7о5 ц);
в 2 2 , 50
п
, . 120
п
, . 208
п
. . 128
1 <РС
°
5 ф =
"бЗ*
693 5005" 3465" 6435"
^п
4
Ф
соз
4
Ф
=--Щ-ВД —зЦд-^ц)
51п
2
фсоз
4
ф = -
п
^-^ Р
4
.
4
(ц) +-|-Рб.
4
(|х));
5т
2
фС05
2
ф = -^Р2.2М+-^-Р
4
.2(ц);
2 2 8
зт
2
фсоз
4
ф = — Р
2 2
(|х) + Р^) —З4б5"
р
в.
31П
4
ф СОЗ
2
Ф = -^-Р
2
.2(Ц) + Д|:(Р
4
.2(ц) —З^5"
Р
Б.2(М.);
1 2 2
С
°
з4 ф =
"105 '
0036 ф =
23Т
Р4
^ Шш
Рб
^'
С08
8
Ф = -щ
Г
Р4.4(^)—(445)
Тогда планетоцентрический радиус трехосного эллипсоида будет
г = а[ с
0
+ СгРг( ц) +
(С2.2
соз
2Х
+ 5
2.2 5112Х)
Рг.2( ц) + с
4
Р
4
(
р.)
+ (с
4 2
соз
2Х
+
+ 5
4
.2 зт 2А,)Р
4 2
( Ц) + (с
4
А соз
АХ
+ 5
4
.
4
зт 4Х)Р
4 4
( (г) + с
6
Рв( Р.) + (СБ.2 соз
2Х
+
+ 5
62
31П
2Х)Рв.
2
( ц) + ( с
6 4
СОЗ АХ
+
«6.4 51П
4Х)Р
64
( (х) + ( СБ.о
СОЗ 6А
+
+ 5
6
.б5т6А,)Р
6
.
6
(р) + СвР8(|х)+(с
8
.2С0й2А, + 5
8
.231п2Х)Р
8
.
2
(ц) +
+ (с
84
соз
АХ
+
58.4 51П
4Х)Р
8
4
(м.)] .
(446)
Коэффициенты с„, с
пт
, з
пт
вычисляются по формулам
» 1 1 о , 1 2 . 3 4 1 2 2 I ^ 4 5 61
б" ~40* 20" ~4(Г
е
~ТТГ +
I 3 42 1 2 4 1 5 6» а 35 6 2 I 1 4 4
+
Ш*
е
~ТГГ
е
+ П2
е
+ТТ5Г 8064~
Г е
+ бГ
8 ;
152

1 2 . 3 4 1 2 3 4
—— е
6
+
175
у
8
—г
6
е
2
+ —у
4
е
4
;
336
т
1584 3168
т
352 '
• 3 '4 , 3 о •) , 9 1 15 к 3 а ') . 3 о 4 ,
б4
= 15
Г
+15 ^ --77^ +176 ^ +
45
6
, Ю5
8
, 15
6 2
333
4 4
.
V
е
А
—х
а
е'
:
——V е
1
1232
1
1144
1
1144 9152
Ь
6
= —V
6
-—\?
4
8
2
—\
2
г
4
+ —V
8
+—У
6
е
2
-
6
231 154 616
т
198
т
396
—у
4
е
4
Ч
—'V
е
Н
—у
6
е
2
+ — у
4
е
4
-
176 ^ 1287 ^ 1287 ^ 572 '
с. 8 I 14 6 2 I ^ 44
6в =
1287
г +
1287"
Л
'
Е +
"572"
У е ;
г 1з 1 2 2 I 3 4 , 5 42 5 24|
Й22
=12
6
-36
г е
+ 67Г
е
--336
г 6
+
I 25 б 25 в 2 • 5 44
~672~ 6336~ ~704~
„2„2 '„4| 3 4 2 5 2„4 5
6
4.2=--
Т17
гГ е' -^8 8 рг^г-г 8
140 280
1
616 1232 1232
15 в 2 I 3 44
4576
1
832
З42 5 24|5Й 1 6 2
Ь
й
2= г
6
е
2
— V V;
82
36052 3432 '
I 1 4 1 04, 5 К . 3 44
К4 =
1240-
8
--9856"
4
'
6
+732Ж
У 6 ;
, 1 24 1 б | 13 44
06.4=
43776
V е 88704-е +
8
23680 *
8 ;
с
п
— л/1 — е
2
6„; с
пт
=л/'
—Е
Ь„
т
со%тк»\
$пт
= V
1
— е
2
й„ш зт тк 0.
Заметим, что в разложении (446) для радиуса трехосного эллип-
соида отсутствуют нечетные зональные гармоники и нечетные тесераль-
ные гармоники. При этом для планетарного эллипсоида разложение
(446) является знакопеременным и быстроубывающим рядом.
4.16.2. Уравнение радиуса двухосного эллипсоида вращения
Для эллипсоида вращения, положив е = 0, получим из формул (439),
(442) и (443) следующие выражения:
153

х
2
+ у
2
+ г
2
/(\-е
2
) = а
2
\
г = а/-\/1 + е'" ап1
2
(р; (448)
е'
2
=е
2
/(1-е
2
).
В частном случае, имея в виду, что е = 0 и х
2
— е'
2
из общих выра-
жений (446) и (447) получим разложение в ряд для радиуса эллип-
соида вращения
г =
а
[
со
+ с
2
Р2( |х) +
С
4
РА(
ц) + с
6
Рб( ц) + с
нР»(
ц)], (449)
где
Со=
1
— е'
2
/6 + Зе'
4
/40 — 5е'
6
/\ 12 + 35е'
8
/1152;'
с
2
= — е'
2
/ 3 + Зе'
4
/14 - 25е'
6
/168 + 175<?'
8
/1584;
с
4
= Зе
/4
/35— 15е
/6
/154+ 105е'
8
/1144;
Св— — 5г'
6
/231 + 7е"198;
с„
= 7е"У1287.
Как видно, разложение (449) для радиуса эллипсоида вращения
представляют только четные зональные гармоники. Это разложение для
планетарного эллипсоида представлено суммой быстроубывающих зна-
копеременных членов. Для Земли (е'
2
= 0,006738, а = 6378км) послед-
ний член |свРвК7-Ю
-5
м, а предпоследний член |с
6
ЯбК42-10~
3
м.
Следовательно, на практике в разложении (449) для радиуса земного
эллипсоида можно пренебречь членами порядка е'
8
и меньшей величины.
Во многих случаях можно исключить и члены порядка е'
6
.
4.17. ПОТЕНЦИАЛ СИЛЫ ТЯЖЕСТИ
УРОВЕННОГО ЭЛЛИПСОИДА ВРАЩЕНИЯ
За основные параметры уровенного эллипсоида примем массу М,
угловую скорость се, коэффициент нулевого порядка /
2
второй гармо-
ники потенциала и экваториальную большую полуось а
е
. Положим, эти
параметры равны соответствующим параметрам планетарного тела,
фигура которого аппроксимируется данным уровенным эллипсоидом.
Для уровенного эллипсоида члены с нечетными зональными гармо-
никами будут отсутствовать, т. е.
Пользуясь формулами из геометрии планетарного эллипсоида
г = а
е
/-^\+е'
2
31П
2
(р; е'
2
=2а + За
2
+ 4<х
3
+... (451)
и, представляя (1+е'
2
51п
2
ф)
т
рядами по степеням е'
2
, получим
1 +-1*'
2
5т
2
<р—1г'
4
51п
4
ф + -1-
<
>'
6
5т
в
ф-...;
(^)
3
=
1
+4«'
2
5>п
2
Ф + -|-г'
4
зт
4
ф+...; (452)
154

(
а
'\ I , 2п+\ ,-2 • 2 , /
("Г/ . ='Н +
Затем подставляя (-у) и полиномы Лажандра в формулу
(450), группируя слагаемые по степеням синуса широты, получим раз-
ложение для потенциала в виде
^ = ^8Ш
2п
ф. (453)
а
' п= 0
Если при этом ограничимся зональными гармониками шестого по-
рядка, то коэффициенты Ш'
п
в уравнении (453) с учетом выражений
будут
+ |-У4+-|/в; (454)
Ш{
- «+-|а
2
+ 2а
3
- ±д - ад —^а
2
д—|-/
2
+ •+
, 9 2, , 30 , 15 . 210. . 70 . ......
а
2
- -§-а
3
—|-аУ
2
- 6а
2
Уг + Щ + \а
1
д -
35 , , 150 , .630 . 1470 , .....
4
Ч——0У4 + -^2"/б зг
-0
^»; (456)
1 з 9
2
, о 2 175 , 462 , , 4410 , ,....
= ——а /г —2а д-а/
4
з^Н—(
457
)
Решая уравнение (453) при условии Ц/=Ш'о=соп51 для любой
точки на уровенном эллипсоиде, получим формулы для согласования
параметров уровенного эллипсоида
8
„з 20 2,
Т
а
"2Г
/
6
=
т
а^-_а
2
<?
;
,4 50 ,
5"
а
+
Т
« 49"
,2 1.3 1 2 25
2
/
2==
_
а
_
т(?+т0и?
__
а
147"®
3 . 1 9 ,2 И
2
3 , . 9 ,2 ,
л.
27
1
3
л.
9
, 93 . ,
+
Тб
У2+
98" "784* '
2 9 . . I 2 , 3 . , 27 ,2 . 27 ,2 11 з 45 .
2
~ Т + Т^ + Т ^ 8" + *56
2<?
~~"56 ^ ~"56
2<?
'
155

, 9 ,2 . 3 2 12 , 27 з , 162 ,
2
27 ,
2
1К/ / 1 1
1
11*1 27 #2 9 2,9 , .
Анализируя результаты, замечаем, что для представления потен-
циала уровенного эллипсоида с учетом членов порядка а" нужно учи-
тывать в разложении (453) зональную гармонику степени 2п включи-
тельно. Уравнения (458), учитывающие члены порядка а
3
, удовлетво-
ряют самым высоким требованиям практики. В нашем случае, когда за
основные параметры принимаются М, /г, а
е
, со, такие параметры как
потенциал сжатие а, четные зональные гармоники У 2л (я = 2, 3,...)
являются производными. Изучая формулы, согласующие основные пара-
метры уровенного эллипсоида с производными его параметрами, нетрудно
убедиться, что за основные параметры можно, например, принять №<>,
а, а
е
, ш и тогда параметры М и /г будут вычисляемыми. Приведен-
ный выбор основных параметров уровенного эллипсоида объясняется
двумя соображениями практического характера. Во-первых, геоцент-
рическая гравитационная постоянная надежно определяется по наблю-
дениям космических аппаратов; второй гармонический коэффициент
в явном виде входит в разложение потенциала ускорения силы тяже-
сти. Во-вторых, вывод согласующих формул выполняется без прибли-
жений, поскольку малый параметр я представляется через исходные
величины.
Как будет видно из дальнейших исследований, значения силы тяже-
сти на экваторе у
е
и на полюсе у
р
также являются производными пара-
метрами.
4.18. НОРМАЛЬНОЕ УСКОРЕНИЕ СИЛЫ ТЯЖЕСТИ
И ЕГО ИЗМЕНЕНИЕ ПО ВЫСОТЕ
Нормальное ускорение силы тяжести, или ускорение силы
тяжести у на уровенном эллипсоиде как градиент потенциала
силы тяжести № равно
+ 1) (
2
"
+2
'2пР,
п
(\1)
1
- Р
2
)9 ] , (459)
где Д<р — разность планетодезической В и планетоцентрической <|>
широт.
156
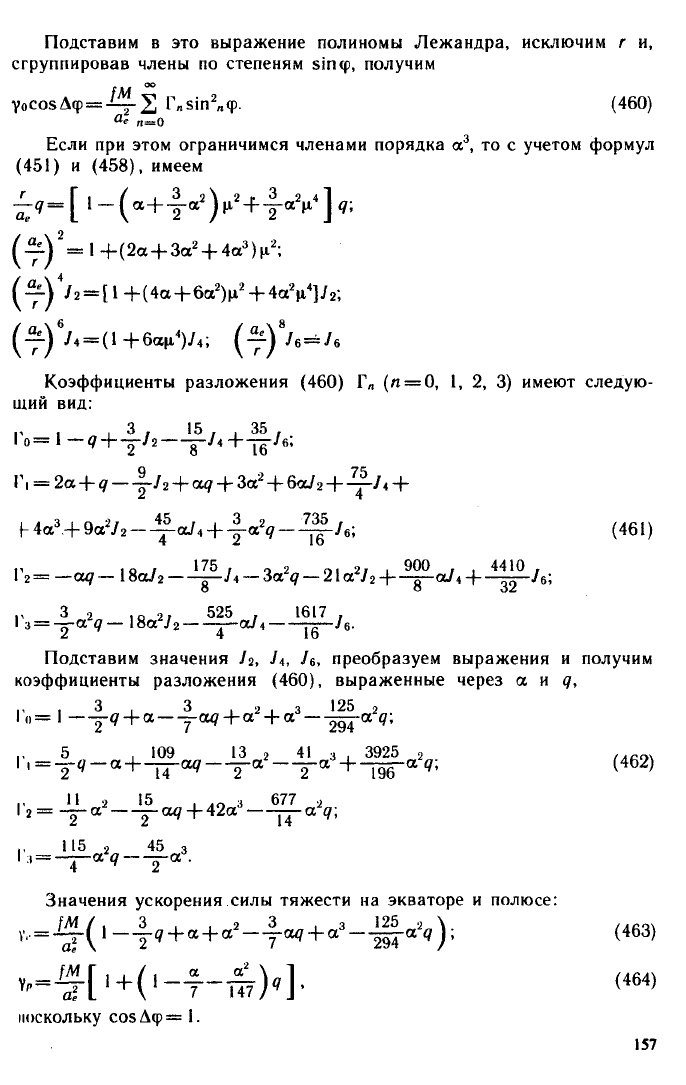
Подставим в это выражение полиномы Лежандра, исключим г и,
сгруппировав члены по степеням зтф, получим
7оСозДф = -^-2 Г„зт
2
„ф. (460)
а
' п—0
Если при этом ограничимся членами порядка а
3
, то с учетом формул
(451) и (458), имеем
(-у)
2
=
1
+(2а + За
2
+ 4а
3
)р
2
;
= +(4а + 6а
2
)ц
2
+ 4а
2
р
4
]У
2
;
(-^)
6
/
4
= (1+6а,х
4
)Д; (-у)'/
б
= /б
Коэффициенты разложения (460) Г„ (я = 0, 1, 2, 3) имеют следую-
щий вид:
Го=
1
— + —
Г,
= 2а + ц - -|-У
2
+
<Щ
+ За
2
+ 6а/
2
+ +
Ма
3
.+ 9а
2
/2-^а/
4
+ 4«
2
<7--^г'* (
461
)
1
,
2=—ом/— 18оь/ 2—— За
2
<? -
21
а
2
У
2
+ -^а/
4
+
3
2
,о 2» 525 , 1617 ,
I
з
= -^-а <7— 18а /г 4—0^4 /е-
Подставим значения У
2
, У
4
, /б, преобразуем выражения и получим
коэффициенты разложения (460), выраженные через а и
I' 1 3 . 3 |
2
|3 125
2
I «= • 2
Я + а + а +а
294"
., 5 .109 13
2
41 з , 3925
2
= щ-—а
2
-—+ (462)
115
2
45 з
I
)==
___
а
д —а .
Значения ускорения силы тяжести на экваторе и полюсе:
§•»+«+«•—!-««+«•—Ц<А|)
: (4Ю|
Н^'+О-т-шМ-
поскольку соз
Дф
= 1.
157

Планетоцентрическая гравитационная постоянная будет
сьл 2 /, , 3 , 9
2
18 , 27 з 153 , . 157
2
\
(М = а
2
еу
е
^1+
т
д-а +
т
д' + —<
хд
2
+—а
2
ду (
46
5)
(466)
(467)
Исключим а в (458) и получим их в другом виде
I
м
( . ,
3
, . 27 ,
2
9
2
, 9 , ,
, 135 з 1
я
з , 123 83 .
2
\ .
+ _
1б"
/2
—588 " 49~ 784" )'
27 ,з , 389 з 57 ,
2
4831 ,
2
\
16"
2
~
4
7&4~
2<!
)
Для планетарного эллипсоида:
Дф= т51п2ф + 'И
2
51п2ф со5 2ф+ ...;
зесДф=
1
+(2т
2
+ 4т
3
)51п
2
ф—(2т
2
+ 12т
3
)5т
4
ф + 8т
3
зт
6
ф + -; (468)
т
2
=а
2
+ а
3
+...; т
3
=а
:!
+ ....
Подставив значения Г, (/ = 0, 1, 2, 3) в формулу (460) и учитывая
выражения (463) и (468), получим формулу для ускорения силы тя-
жести на уровенном эллипсоиде
70=7*0 +Р28т
2
ф + Р55т
4
ф + Р^зт
б
ф + ...); (469)
где
а/ 5 .53 ,152 7 2 о з I 45 з , « •> . 248 •>
р2
=
"2"<7
- «+ + — Я ~ « - 8« + + Зои?
2
+ — а
2
?;
«'-
15
„ „, 7 „г, 41
3
45 , 773 ,
р
4
=
т
ш1 +
т
а +~а —ад —а д,
В
'_
95
„2
л
25
„з
Рб = — а д 2~а ,
Правая часть этого выражения представлена через четные степени сину-
са планетоцентрической широты. Ее также можно представить через
четные степени синуса планетодезической широты В, пользуясь разло-
жениями
5Ш
2
ф
=
(1 —
а)
4
(з1П
2
б + ез1П
4
В + е
2
5!П
6
в+...);
51П
4
ф
=
(1 —
а)
8
(зт
4
В+2езт
6
в +
.-.);
(470)
зт
в
ф=зт
6
В+...; е = 4а—6а+4а
3
.
Исключив зтф в уравнении (469) и преобразуя его, получим
70
= 7,(1 +Р2зт
2
В + Р45!П
4
В+Рб5т
6
В + ...);
5 87 , 15 а , 1 2 , 45 з а , 241 2
158

„ 5 1 2 I 1 з 209 2 , 15 2
р
4
= —а</ 2 +Т 28~
аЯ +
Т
Щ
'
= (471)
Правая часть этих уравнений представлена через четные степени синуса
планетодезической широты.
Гравиметрическое сжатие составляет
р = р
2
+
р
4
+ р
6
+ + + ...,
или
О 5 . 15 2 26 . 45 з 33 2 . 59 2 ,л-,™
Рассмотрим изменение нормального ускорения силы тяжести
У={
1
-
п
|
1
(2«+1)(^)/
2
^2П(Ц) ] —^гсоз^} зесДф
(473)
по высоте. Принимая высоту точки над уровенным эллипсоидом за
малую величину по сравнению с геоцентрическим радиусом г, восполь-
зуемся разложением в ряд по малому аргументу
У-У-Щ. 2 (-5есДф)*
+,
Г
<*
+ .)-2 ^Щ^-Х
г 1
*=1 (1=1
Лп
-
К
-
X (•^'"/аА.м] (4)*+(-^-)
3
<7(созфзесДф)
2
^-} , (474)
где уо — значение нормального ускорения силы тяжести на уровенном
эллипсоиде.
Как видно из (474) и данных табл. 11, градиент силы тяжести зави-
сит от высоты. Кроме того с увеличением высоты сходимость разло-
жения (474) замедляется. Поэтому им можно пользоваться только для
малых высот или когда не требуется высокая точность в вычислениях.
В приближенных расчетах градиент силы тяжести вычисляют по фор-
муле
ду/дН= — (0,308 827 30
—
0,0001446// км) Ю^см-с
-2
/". (475)
Если в вычислениях необходима высокая точность, то следует поль-
зоваться формулой (473). Третий член ряда (п—3) по величине не пре-
вышает 0,013-Ю
-3
см-с
-2
, поэтому достаточно ограничиться учетом
малого члена с коэффициентом /
4
«2/
2
.
Заметим, что с увеличением высоты точки медленно уменьшается
угол между геоцентрическим радиусом и нормалью к эллипсоиду. Так
например, на высоте 100 км угол равен 11,4', а на высоте 33 тыс. км —
1,9'.
159
