Машимов М.М. Геодезия.Теоретическая геодезия
Подождите немного. Документ загружается.


Таблица
10
(М = 398 600,5 км
3
/с
2
; а„ = 6 378 140 м; е
2
= 0,006 694 384 872;
У
2
= 1082,63- Ю-
6
; = -2,370 97-10"
6
; /
6
= 0,006 02- Ю"
6
;
д = 0,003 461 396 277; В =45°; N = а(1 — е
2
51пВ)-'/
2
;
'-е
2
м
+ Н
) гсо8
Ф
= (Л' + Я)со5в.
Обозначения
й=0м
Н = 2500 м
И = 5000 м
Ы +
Н,
м
Ф
г, м
(М/г, м
2
/с
2
6 388 641,303
44°48'27,2759"
6 367 492,531
62 599 288,1894
6 391 341,303
44
с
48'27,5478"
6 369 992,517
62 574 720,2899
6 393 841,303
44<Ч8'27,8194"
6 372 492,503
62 550 171,6659
1 /М
2 2
СОЗ ф
54 261,4291 54 303,9092
54 346,3939
и
62 636 831,5383 62 612 325,7098
62 587 839,1281
эй з
7 =
~д77'
10 см
'
с
"
' 980 618,9109
979 847,9673 979 077,9985
~1ПР~
=
Ш'
10_3 см
"
с_2
/
м
0,308 827 30
0,308 464 85
0,308 106 43
4.19. КРИВИЗНА СИЛОВОЙ ЛИНИИ.
КООРДИНАТНЫЕ ПОВЕРХНОСТИ И ЛИНИИ
Определим кривизну силовой линии. Вектором кривизны линии на-
зывается предел отношения приращения единичного вектора касатель-
ной т_к приращению йк длины линии, когда Лк стремится к нулю, т. е.
е/р
= йуйк, (476)
где е — диничный вектор главной нормали линии; р — радиус кривизны
линии.
Единичный вектор касательной к силовой линии т = отсюда
1 8, а§
е лн е- ан
Поскольку
5
= —аш/ак,
имеем
(1х _ 1 / д
2
УР . д
2
УР . д
2
Г . \ _
ЛИ ~ в \ дхдН '
+
дуд/г *
+
дгдН )
160

Совместим ось г с направлением, противоположным направлению
силы тяжести, и вычислим производные
дх ' ди ' дг дхдН дхдг '
(478)
д
2
у <э
2
1г
дудН дудг ' дгдН дЬ
2
Подставляя найденные значения производных в уравнение (477), с
учетом (476), получим
е 1 / <Э
2
1Г . . <3
2
1Г
/ч
_
0
.
(478)
Отсюда заключаем, что отвесная линия имеет двойную кривизну.
Если ось х направим на север, а ось у — на восток, то на поверх-
ности эллипсоида
ах
=
мав-, Лу
=
л/соз
вац
д
2
ц ду
0
ду
п
дЦ дуо ду
0
дхдг
~ дх ~ МдВ ' дудг ~ ду ~ ~ ЫсоъВсИ '
С учетом выражения (471)
-Й-ТАЧпЭД 0.
Подставив значения производных в уравнение (478), получим
или
1/р=р
2
зт2 В/М. (480)
Отсюда следует, что силовая линия нормального поля — кривая, лежа-
щая в плоскости меридиана, кривизна которой изменяется с изменением
широты. Приняв М = 6371 км, |}
2
= 0,005 279, В =45°, находим, что
радиус кривизны силовой линии нормального поля р = 1 206 857 км.
Отрезок силовой линии практически не отличается от отрезка нормали к
уровенному эллипсоиду вращения.
Семейство уровенных поверхностей и силовых линий нормального
потенциала можно использовать в качестве координатных поверхностей
и линий, определяющих положение точки планетарной поверхности или
пространства.
Уравнение семейства уровенных поверхностей нормального потен-
циала имеет вид II = сопз!. Поскольку на поверхности уровенного
эллипсоида нормальный потенциал равен IIо, для определения уровен-
ной поверхности точки <3, находящейся на высоте Н от поверхности
эллипсоида (рис. 25), достаточно определить разность нормальных по-
тенциалов и о—У о. Долготой точки определяется меридианное сече-
6-М. Машимов
161

Рис. 25. Связь геодезической и нор-
мальной широт
ние поверхности
(У
=(/<? = сопз1, а точка <2' определяется как точка
пересечения меридиана и силовой линии. Угол, образованный касатель-
ной к силовой с экватором, назовем нормальной широтой и обозначим
через В
п
. Отрезок линии
С1'С1
= (11о—1>о)/у т, где ут — значение нор-
мального ускорения силы тяжести в точке, находящейся в середине
отрезка линии (?'(? = Н
п
- При этом
у
т
= у
е
(
1
+ р
2
51П
2
В + р
4
5Ш
4
+
Докажем, что отрезок силовой линии Н
п
можно заменить геодезической
высотой Н = Из рис. 25 следует, что умножив разность нормаль-
ных широт В
п
—
В'
п
точек
С?
и С}' на радиус кривизны силовой линии р,
получим нормальную высоту
Нп = р(В
п
-В'„). (481)
Из треугольника Я<ЗС?о находим
Н = рзт (В
п
-
В'„)
=
р(Вп
-В'
п
)~ р (
в
"~
в
")
3
,
откуда
Нп-Н=р(В
п
-В'п)
3
/&.
Подставляя значения р (480) и В
п
—
В'
п
(481), получим
Н
п
—
Н= &
2
2
НЫп
2
2В/6Я
2
. (482)
Положим для Земли Н
п
— 10 км, В =45°. Известно, что Р/рзт2В =
= 1,2-10
6
км, следовательно, Н
п
— И= 10
3
/6• 1,44-10'
2
« 0,12- Ю
-9
м.
Поэтому не будем различать геодезическую высоту и соответствующий
отрезок силовой линии Я„. Таким образом, геодезическая высота
Н = (У
0
-и<))/у
т
(483)
162

может служить координатой точки <2, заменяя разность потенциалов
1/о—*/<?.
Выведем формулу для перехода от нормальной широты В„ к геоде-
зической широте В точки <2.
Представив искомую разность в виде
В-В
п
= (В-В'
п
)-(В
п
-В'
п
),
подставим значение
В
п
— В'
п
= р
2
Язт 2В/Я, (484)
тогда
В —
Вп
= {В — В'п)~ р
2
//зт 2В/Я-
Теперь остается определить малый угол В—В'
п
. Из треугольника
(.Э"<?о<Э' отрезок
(2о<3'
= Я(В —
В'„).
Кроме того,
С?о<3'
= р - рсоз (Вп - В'п) = р(Вп- В'п)
2
/2.
Следовательно искомая разность углов будет
В-В'п=^-(Вп-В'п)
2
= 2р
2
51п 2В (
В
"-
В
»)
2
'
или с учетом (484)
В-В'
п
=^т2В.
Окончательно
й-б„=-М-зт2В(1-^-). (485)
Оценим правую часть формулы (485). Положим Н = 10 км, В — 45°,
Я = 6371 км, |}
2
= 0,005 279. Первый член —(р
2
Я/Я)рзт 2В=—1,7091"
(р= 206 265), второй член р
2
Я
2
зт 2В/2Я
2
= 0,0013", следовательно для
Земли можно пользоваться формулой
В = В
п
—
(0,170 91 —0,000 013Я)Язт 2В, (486)
где Я — высота точки в километрах.
Во многих случаях практики второй поправкой можно пренебречь.
4.2;. ПОТЕНЦИАЛ СИЛЫ ТЯЖЕСТИ ТРЕХОСНОГО ЭЛЛИПСОИДА
Сложив правые части уравнений (97), (155) и учитывая свойства
трехосного эллипсоида, потенциал силы тяжести на его поверхности
запишем
6*
163

= у
2 2С05
2к + Кг.иып 2Х)Р
2
.2(|х)] -
-{-^[иРМ+и^сов
2К
+
КА.2&Ш
2^)Я
4 2
(Ц)+(У
4
.
4
С05
4Х
+
+ /С
4 4
31П 4Х)Р
4
.4(м-)] -(-^)
7
[/в/
,
б(ц) + (/б.2С05
2Х
+ /С
6
.
2
5т 2\)Р
6 2
(|Х) +
+ (У
64
со54>. + /(в.
4
31п4Х)Я
6
.
4
(ц)]+^-
<?
(-5-)(1-ц
2
)} . (487)
Представив выражение (441) в виде
— == 'V
1
+ = V
1
- * = "
2
з!п
2
Ф—
Г
2 2
(488)
и
2
= +е
2
С05
2
(Я.->ю); У
2
= е
2
соз
2
(х-х,о),
1
—е
запишем следующие разложения:
Т—"О
(тУ-^т^-^У
=
(489)
/ а \
7
_
7
/ . . 7 ,35 2 , 35 з\
Подставим выражения (489) в правую часть формулы (487) и
исключим сферические функции Р
П
т(\»), подставляя их значения (466).
Выполняя преобразования и группируя члены по степеням синуса широ-
ты, получим разложение потенциала
Г = Г'изт^ф. (490)
а
" п = 0
Коэффициенты разложения Щ (п = 0, 1, ..., 4) имеют значения:
х(±/2-зи
2
)
1
_(т
и
~т
и2+105/
-
44
) +
, _
7
/ . 7 2, 35 Л/ 5 , 105 , . 945 , \ .
^ V Г / ("16
6
8~
62
~' 2~
6 4
) +
164
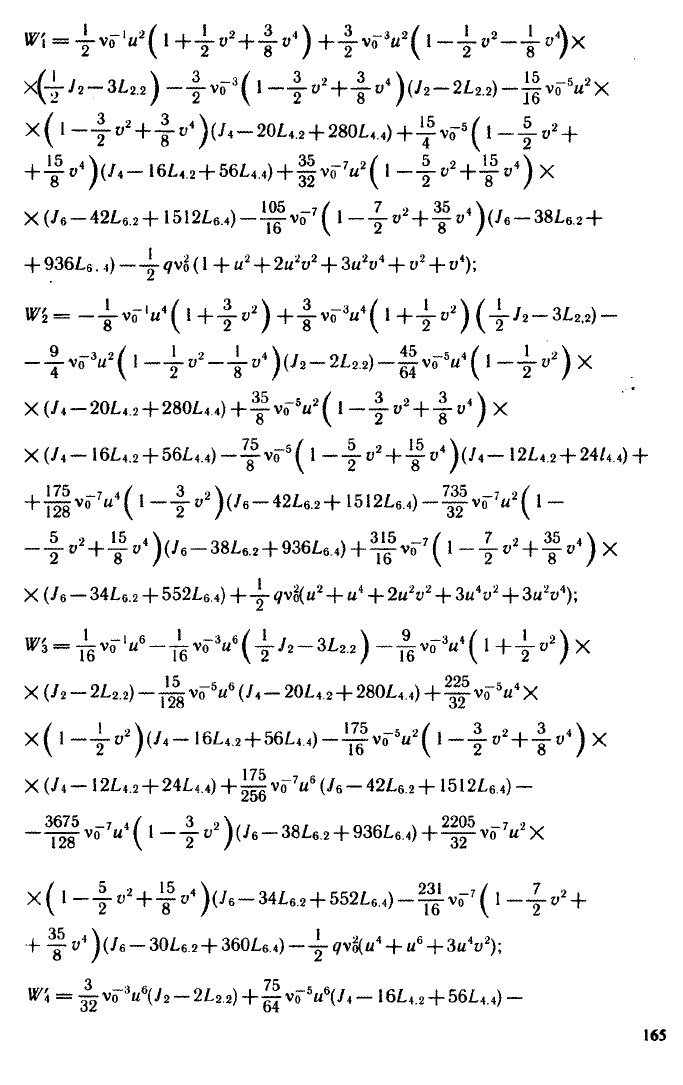
х(4" -
2
) - 4 ^о-
3
(
1
—|
у2
+ 4 °
4
) - 2^2.2) - Л X
х(1—у«
2
+ 4
у4
)
(/4
~
2ои 2 + 28ои<)
+ Т ^ (
1 -
Т +
+ ^ о
4
) (л -
1
би
2
+ 56^.4) +§ *<г V (I - -+) х
X (/. •- 421
6
.2 + 1512/.
6
,4) —^ го"
7
(
1
- + ^ ) (•'в - 38^
62
+
+ 9361.6.4) И
(1
+ и
2
+ 2« V + 3 и V + у
2
+ у
4
);
Щ
=
-4-*О-'«
4
(
1
+
-|го-
3
«
4
(
1
+-у°
2
) (т
/2
-
3122
>-
-т
Го_3
"
2
(
1
-Т
о2
-т
у4
)
(/2
~
2
^
2 2)
-1
л,
°"
5
"
4
(> НИ
х
X (/4 - 20/.4.2 + 280/-4.4) + ^ (1—+
Х(Л- 16/.
4
.2 + 5би
4
)-^^
5
(
1
+ о
4
)(7«- 12/.4.2 + 24/4
4
) +
+
И
Уо
"
7
"
4
(
1
- т
у2
)
(/б
~
42
^
6 2+
1512/
-
6 4)
-
7
-§^
7и
'
2
(
1
-
—§-"*+Т
у4
)(
у
6-38/.6.2 + 9361..4) + ^го-
7
(
1
—^ + X
у4
) X
X (/е - 34/-6.2 + 552/.
64
) + -у + и
4
+ 2и V + Зи V + За V);
Щ = Vо-
11
и
6
—1 *<Г V ( 4 ~ 3/-2.2 ) —| ^о-
3
м
4
( 1+ ) X
X и2 - 2Ц
Л
) - щ чо
6
и
6
(/«- 20/.4.2 + 280/.4.4) + Ц у(Г V X
х( 1 -у 16/.42 + 56У.44)—^о"
5
^ 1 —|
у2
+ Т
у4
)
Х
X (/4 -
121-4.2
+ 24У.4.4) +
л
'в"
7
"
6
(
/б
-
42/
-
6 2
+
151
<) -
-^Г
Уо_7
"
4
(
1
-4.
2
)(/в-381,2 + 93би4)+^г
0
-
7
«
2
Х
Х(
1
-4
у2
Ч
у4
)
(Уб
~
34и2 + 5521б4
>-^
0_7
(
1
~Т
у2 +
+ ^ О
4
) (/в - 30/.6.2 + 360/.
6
.
4
) - 4" <М"
4
+ "
6
+ ЗИ
4
У
2
);
8=8
Ж -
2^-я.я)
^
5
М
6
(/4 -
I 6У.4.2
+ 5614.4) ~
165

-|^о-
5
«
4
( 1 1 чи
л
+ 241.4.4)го-
7
«
6
( 1 X
X (/в - 38/-6.2 + 9361б.4) + чо
7
и* (
1
—| У
2
)(У
6
- 34/.
6 2
+ 552Ц
Л
) -
1617 _
7 2
-Го
V ( 1 - 1>
2
+ о
4
) (Уб - 301б.2 + 360/.6.4) + -у дхЫ
6
-,
32
1*пт
= У
ЛТ
С05
/пА,
+ К
пт
8!П тк. (491)
Коэффициент нулевого порядка Щ можно вычислить, положив ф = О
в исходном уравнении (487) и разложив его правую часть по малому
параметру V
2
= е
2
соз
2
(к—
ко).
Потенциал уровенного трехосного эллип-
соида
Г = Го = [М
Ш'о/а
2
= сопз1,
следовательно, его параметры должны удовлетворять условию
Щ = 0, / Ф 0. (492)
Для двухосного эллипсоида параметры: и = е', е = 0, у
0
=1, А,
0
= 0,
]пт = Кпт — 0, а коэффициенты разложения потенциала имеют значе-
ния:
1+4-У2—|"У4 + -^Уб + 4-<7;
105 , 1 1 ,
2
—Те1*-
Т
я-
Т
яе ;
т = —1 е'
4
+ ±
е
'
4
У
2
—1 е'
2
У
2
- § У4в'
4
+ Ц-У
4
е'
2
- Щ У
4
+
, 175 /4, 735 .о» , 315, , 1 . 1 ,4
728 32"
е Уб
+ 1б"
Уб
+Т
е
" +
1К// 1 ./6 ' 9
/4
, 15
/6
, , 225
/4
, 175 ,
2
, ,
Гз =
Тб
е
32
У2_
Тб
е
128
/4+
12"
е 4
26~
У4 +
, 175 3675
/4
, . 2205
/2
, 231 , 1 ,
4
1 ,
6
256
6
Г28"
6
32~
6
15"
6
2~
|к/' 3 ,в# _1 75
,6
/ 525
/4
, 3675
/6
, , 11 025
/4
,
=
1(2
2
64
У4_
"(Й* Г28
Уб_
1617 ,
2
, . 1
32
е ]
ъ + Т1
е (492)
Заменив в формулах (492) второй эксцентриситет через е'
2
=2а +
-|-За
2
+ 4а
3
и удержав члены порядка а
3
, можно получить формулы
(454) —(457).
166

4.21. УРАВНЕНИЕ ПЛАНЕТАРНОГО ГЕОИДА
И ВЫСОТА ГЕОИДА НАД УРОВЕННЫМ ЭЛЛИПСОИДОМ
Положим известны стоксовые постоянные ]„
т
, Кпт, параметры (М,
а
е
, о, геоцентрические координаты г,-, ф,-, X,- пространственных точек
(г = 1,. 2, ..., к) и их высота Ы над уровнем моря. Требуется опреде-
лить потенциал на поверхности геоида, уравнение геоида и его высо-
ту над уровенным эллипсоидом. Потенциал ускорения силы тяжести на
поверхности геоида определяется из выражения
V 0=Щ 1- 5 (— У 2 (УПТСОЗ ТХ + ЛЛТЗШ ТК)РПТ($'Т Ф) +
г
е
I. п =
2 ^
Г
е ' т=
О
(493)
Геоцентрический радиус проекции точки <3 на геоид по радиусу-вектору
будет
г
в
— г — Нзес (г, Н). (494)
Для каждой точки, вычислив геоцентрический радиус г
в
,- и значение
потенциала Шы (*=1, 2, ...), определим средневесовое значение
Затем вычислим масштабный множитель
/М/Го (495)
и радиус-вектор произвольной точки геоида по формуле
/а
п
1 — 2 ( — ) 2 (•/птсоз т'к + Кпт$т тк)Р
пт
(ъ\п ф) +
„=2
4
' т = О
+тЧ^)
3с082(р
]-
(496)
Таким образом, геоид представляется семейством точек с геоцентри-
ческими координатами г
е
, ф, X. При этом геоцентрический радиус каж-
дой точки геоида вычисляется по формуле (496) по исходным парамет-
рам }М, (1е, 0), 3пт, Кпт•
В правой части этой формулы стоит определяемая величина г
д
.
Исключим г
й
, подставляя г
е
=
/"о
+ е, где г о— геоцентрический радиус
точки на поверхности уровенного эллипсоида; § — высота геоида, по
величине не превышающая 100—120 м. Оценим второй член в разло-
жении формулы (496)
= ^ ^ [ ^ ( )
Зс052 ф
) ^
2 (381
"
2 ф _ 1)
] '
подставив /"
й
=го + е. Остальные члены настолько малы по отношению
ко второму члену, что для них можно принять г
е
= г
о.
Заметим, что /?
г
« а
е
ж г
0
167

(
г
' ) [
го
+
?
)
г
° )
2 Го
'
\а
е
) \ а
е
/ \а«/ г
0
Тогда второй член примет вид
вг = у[
<?
("Н7 )^оз
2
Ф
- ()
2/2
(
Зз|п2
ф -
1
) ] + Т «
9С052 ф
+
+ (г
е
— ГО)
^ ?соз
2
ф
4- У
2
(Ззш
2
ф —
1) ^ .
Обозначим
[
- / а \" "
1— 2 (т") 2 (/ятСОЗ
/пА,
+ /С„
т
51П тЯ.)Рлт(5т ф) +
п=2
\ '0 /
т =
0
+т
9
(0'
СО52ф
]
;
<
497
>
V = -|-</С05
2
ф + /
2
(35т
2
ф— 1) (498)
и подставим значение бг в формулу (496). Получим выражение
/ а \" "
1
— 2 ( — ) 2 (УптСоз + /0,
т
зт тХ)/
,
пт
(51п ф) +
п-2^
Го
>
т
— 0
+ 4-'?(-^)
3со82
Ф] (499)
для вычисления геоцентрического радиуса точки геоида.
Положим У
2
= 0,001 08, д = 0,00346,
г
0
ш
—
г
0
= 100 м. Тогда поправоч-
ный член
—
7"о)"У|пах
=
0,4 м. В точных работах поправочный член
необходимо учитывать.
Высоту геоида вычислим по формуле д = (г
8
—
го)со8(го, и). Посколь-
ку (
г
«)
г
) « 100 м, |1
—
соз(г
0
, п)| = 0,000 005, можно принять
Я
= г
в
— г
0
. (500)
Значения геоцентрических радиусов вычисляются по формулам
(451) и (499).
Рассмотренным способом можно наиболее просто и строго вычислять
геоцентрический радиус и высоту геоида. Самая обширная и полная
информация о профилях геоида получается при спутниковом нивелиро-
вании и поэтому оно на современном этапе самое мощное средство опре-
деления потенциала планетарного геоида. Кроме того, спутниковое неве-
лирование позволяет уточнять коэффициенты У„
ш
, Кпт, из решения
обратной задачи, и таким образом устанавливать значение потенциала
Го на каждую эпоху, а следовательно, все параметры планетарного
геоида.
168

4.22. ДИФФЕРЕНЦИАЛЬНЫЕ СОСТАВЛЯЮЩИЕ НОРМАЛЬНОГО
ПОТЕНЦИАЛА. ФОРМУЛА ГЕОДЕЗИЧЕСКОЙ ВЫСОТЫ
Нормальный потенциал (У уровенного общего земного эллипсоида
разложим по степеням геодезической высоты Н в ряд с учетом членов
третьего порядка
11 — 11 Л.
ди
НЛ.
1 д
*
и
Н* Л.
1
,г
П
ц
+
+ Н +- — Н, (501)
где Со — нормальный потенциал на поверхности эллипсоида.
Приняв V я*[М/г и у«/М/г
2
, оценим кубический член
1 дЮ „з 1
6 дН
3
Если положить Н = 6 км, г = 6000 км, у = 1000 см/с
2
, то кубический
член (501), поделенный на г, по абсолютной величине не превышает
0,000 001 см/с
2
. Поэтому его можно отбросить.
Объединим второй и третий члены разложения (501) и получим
/ дЦ . д
2
С/ Н \ „ „
где у
т
— нормальная сила тяжести в точке с высотой Я/2.
С учетом (502) разложение (501) напишем в дифференциальной
форме
= (503)
Отсюда получаем формулу геодезической высоты относительно общего
земного эллипсоида
Я = (Со-{У)/?т. (504)
Если центр уровенного эллипсоида смещен от центра инерции Земли
на Аг(Ахо, йуо, с1г
0
), то необходимо учитывать приращения потенциала
притяжения
д и
г
= —(М(Хёх 0+ Уйу
0
+ 2с1г
0
)/г
Л
(505)
и потенциала центробежной силы
М]
и
, = а%Хйх
о
+ уауо). (506)
Если Дг = 0,3 км, г = 6000 км, у = Ю00 см/с
2
, ш
2
= 0,5- Ю
-8
с
-2
, то
АН,/г = 0,05 см/с
2
и М1
ш
/г = 0,00015 см/с
2
. При современных точно-
стях измерений необходимо учитывать обе эти поправки.
Имея в виду, что X = гсоз Всоз У = гсоз Взт 7. = гзт В и
у « {М/г
2
, формулы (505) и (506) запишем так
Д/У
г
= —у(йх
0
со& Всоз Ь-\-с1уосо$ бзт
1,
+ йгозт В), (507)
АС1„,
=
ГЫ
2
(АХОС05
Всоз +
Й(/ОСОЗ
Взт /.). (508)
169
