Marsh D. Applied Geometry for Computer Graphics and CAD
Подождите немного. Документ загружается.

Solutions 329
Chapter 4
4.1.
⎛
⎝
−127 −33 −3
24 11 12
−10 −55 −126
⎞
⎠
.
4.2.
⎛
⎝
−10 −14 0
−15 −21 0
−64−31
⎞
⎠
.
4.3. M =
⎛
⎝
−12 −31
−7 −16 −1
63 −27 −10
⎞
⎠
,andA
−
5
2
,
13
2
, B
2
3
,
29
3
, C
2
3
,
29
3
.
4.4. M =
⎛
⎝
480
120
−8326
⎞
⎠
,andA
1
3
,
26
3
, B
11
6
,
35
3
, C
3
2
, 11
.
4.6.
⎛
⎜
⎜
⎝
51−1 −1
6433
4 −292
−84−43
⎞
⎟
⎟
⎠
.
4.8.
⎛
⎜
⎜
⎝
−5000
2 −96 0
3 −64 0
4 −812−5
⎞
⎟
⎟
⎠
.
4.10. For Exercise 4.6: A
(−8/3, 4/3, −4/3), B
(−3/2, 5/2, −5/2),
C
(−1/3, −4/3, −1/6), D
(1, 1, 1).
For Exercise 4.8: A
(−4/5, 8/5, −12/5), B
(1/5, 8/5, −12/5),
C
(−6/5, 17/5, −18/5), D
(−4/5, 23/5, −22/5).
4.12. K =
⎛
⎝
12/13 5/1300
−5/13 12/13 0 0
4301
⎞
⎠
, VC=
⎛
⎜
⎜
⎝
12/13 −5/13 0
5/13 12/13 0
000
−63/13 −16/13 1
⎞
⎟
⎟
⎠
,
giving A
(−63/11, −16/13), B
(−3, −2), C
(−24/13, 10/13), and
D
(−48/13, 20/13), E
(−97/26, −15/13), F
(−56/13, −33/13).
330 Solutions
4.13.
K =
⎛
⎝
3/
√
34 0 5/
√
34 0
0 −100
−11 11
⎞
⎠
,
VC =
⎛
⎜
⎜
⎝
11
98
√
34 −20/49 −20/49
0 −10
13
98
√
34 12/49 12/49
−
1
49
√
34 17/49 17/49
⎞
⎟
⎟
⎠
.
Images of vertices:
−
1
17
√
34, −
32
17
,
−
22
31
√
34,
80
31
,(0, 2),
−
3
2
√
34,
103
5
.
4.15. M=
⎛
⎜
⎜
⎝
−12 0 0 0
0 −12 0 0
23−41
81232−8
⎞
⎟
⎟
⎠
, VC=
⎛
⎜
⎜
⎝
0.7071 −0.7071 0
0.7071 0.7071 0
−0.1664 0.4991 −0.2353
0.0416 −0.1248 0.0588
⎞
⎟
⎟
⎠
,
DC =
⎛
⎝
80 0 0
0800
480 860 1
⎞
⎠
, VP =
⎛
⎜
⎜
⎝
−678.8225 678.8225 0
−678.8225 −678.8225 0
819.4113 746.8629 1
−3161.1775 −5296.0808 −8
⎞
⎟
⎟
⎠
.
Then A
(431.51, 552.91), B
(625.46, 358.96), C
(722.44, 649.89), and
D
(593.14, 520.59).
4.16. M =
⎛
⎜
⎜
⎝
1011
−7 −6 −1 −1
00−60
−70−1 −7
⎞
⎟
⎟
⎠
, VC =
⎛
⎜
⎜
⎝
0 −0.333 0.333
1.414 0.333 −0.333
010
−1.414 −0.667 0.667
⎞
⎟
⎟
⎠
,
DC =
⎛
⎝
25 0 0
0 100/90
100 250/31
⎞
⎠
, VP =
⎛
⎜
⎜
⎝
64.645 83.333 1
−276.777 −83.333 −1
0 −66.667 0
−452.513 −516.667 −7
⎞
⎟
⎟
⎠
.
A
(64.65, 83.33), B
(11.61, 133.33), C
(185.86, 102.38), D
(64.64, 116.67).
4.18. Consider the line segment through P(p
1
,p
2
,p
3
) in direction (v
1
,v
2
,v
3
),
from P to Q(p
1
+ tv
1
,p
2
+ tv
2
,p
3
+ tv
3
). The line segment has length
|t||(v
1
,v
2
,v
3
)|.Then
QM =(p
1
+ tv
1
,p
2
+ tv
2
,p
3
+ tv
3
, 1)M = PM + t(v
1
,v
2
,v
3
, 0)M .
The image of the segment has length |QM − PM| = |t||(v
1
,v
2
,v
3
, 0)M|.
The foreshortening ratio is |(v
1
,v
2
,v
3
, 0)M|/|(v
1
,v
2
,v
3
)| which depends
only on (v
1
,v
2
,v
3
). Therefore all segments with the same direction have
the same foreshortening ratio.
Solutions 331
4.19. Use the solution to Exercise 4.18. The direction of the x-axis is
(v
1
,v
2
,v
3
)=(1, 0, 0). Then
(v
1
,v
2
,v
3
, 0)M =(1000)M =
n
2
2
+ n
2
3
− n
1
n
2
− n
1
n
3
0
which has magnitude
n
2
2
+ n
2
3
1/2
n
2
1
+ n
2
2
+ n
2
3
1/2
=
n
2
2
+ n
2
3
1/2
.
The foreshortening ratio is |(v
1
v
2
v
3
0)M|/|(1, 0, 0)| =
n
2
2
+ n
2
3
1/2
.
Similarly for the other principal directions.
4.20. Let P (xyzw) be a point in the viewplane in world coordinates and let
the corresponding viewplane coordinates be (XY W). Then (xyzw)=
Xr
1
+ Ys
1
+ Wq
0
Xr
2
+ Ys
2
+ Wq
0
Xr
3
+ Ys
3
+ Wq
0
W
.
Then (xyzw) is a point at infinity if and only if (XY W) is a point at
infinity. Similarly for the device coordinate transformation.
Chapter 5
5.1. (((6t − 2) t +4)t − 5) t + 3 requires 4 ×’s and 4 ±’s. 3 − 5 · t +4· t · t −
2 · t · t · t +6· t · t · t · t requires 10 ×’s and 4 ±’s.
5.3. Horner requires n ×’s and n ±’s. The ordinary method requires n(n+1)/2
×’s and n ±’s. Saving n(n − 1)/2 ×’s – quite a saving!
5.5. (a) t(u)=(x(t)+ux
(t),y(t)+uy
(t)). (c) x
(t)x + y
(t)y + y
(t)y(t) −
x
(t)x(t)=0.
5.6. (a)(i) (1, 1) corresponds to t = 1; unit tangent is t(t)=
1/
√
1+4t
2
,
2t/
√
1+4t
2
,andsot(1) =
1/
√
5, 2/
√
5
. (ii) n(1) =
−2/
√
5, 1/
√
5
.
(iii) 2/
√
5(x − 1) − 1/
√
5(y − 1) = 0.
(c) (i) t(t)=
1
√
1+b
2
(b cos t − sin t, b sin t +cost) .
(ii) n(t)=
1
√
1+b
2
(−b sin t − cos t, b cos t − sin t) .
(iii) (b sin t +cost)(x − x(t)) − (b cos t − sin t)(y − y(t)) = 0.
(d) (i) t(t)=
1
√
2+2 cos t
(1 + cos t, sin t) .
(ii) n(t)=
1
√
2+2 cos t
(−sin t, 1+cost).
(iii) sin t(x − x(t)) − (1 + cos t)(y − y(t)) = 0.

332 Solutions
5.8. Rotation of C(t)=(x(t),y(t)) is the curve R(t)=(x(t)cosθ −y(t)sinθ,
x sin θ + y cos θ). Then
R
(t)=(x
(t)cosθ − y
(t)sinθ, x
(t)sinθ + y
(t)cosθ) .
Then speed of R(t)is
(x
(t)cosθ − y
(t)sinθ)
2
+(x
(t)sinθ + y
(t)cosθ)
2
=
(x
(t))
2
+(y
(t))
2
which is the speed of C(t).
5.10. (a) L
C
(t)=
t
−π
(1 + cos u)
2
+ (sin u)
2
du = 4 sin
1
2
t +4.
(c) L
C
(t)=
t
t
0
sinh
u
c
2
+1 du =
t
t
0
cosh
u
c
du =sinh
t
c
−
sinh
t
0
c
.
(e) L
C
(t)=a
√
1+b
2
t
t
0
e
bu
du =
a
b
√
1+b
2
e
bt
− e
bt
0
.
5.11. 8.
5.14. (a) Take t
0
= 0 so that s(t)=L
C
(t)=4sin
1
2
t.Thent = 2 arcsin
1
4
s and
reparametrization gives
2 arcsin
1
4
s +sin
2 arcsin
1
4
s
, 1 − cos
2 arcsin
1
4
s
.
(c) Take t
0
= 0 so that s(t) = sinh
t
c
.Thent = c arcsinh s,and
reparametrization gives (c cosh (arcsinh s) ,carcsinh s) which simplifies to
c
1+s
2
,carcsinh s
.
5.15. (x
(t),y
(t)) =
−3+6t, 6t − 6t
2
, n(t)=
1
1−2t+2t
2
−2t +2t
2
, −1+2t
.
Then the offset is
1 − 3t +3t
2
, 3t
2
− 2t
3
+
d
1 − 2t +2t
2
−2t +2t
2
, −1+2t
.
The curve and an offset are shown in the following figure.
1
2
2
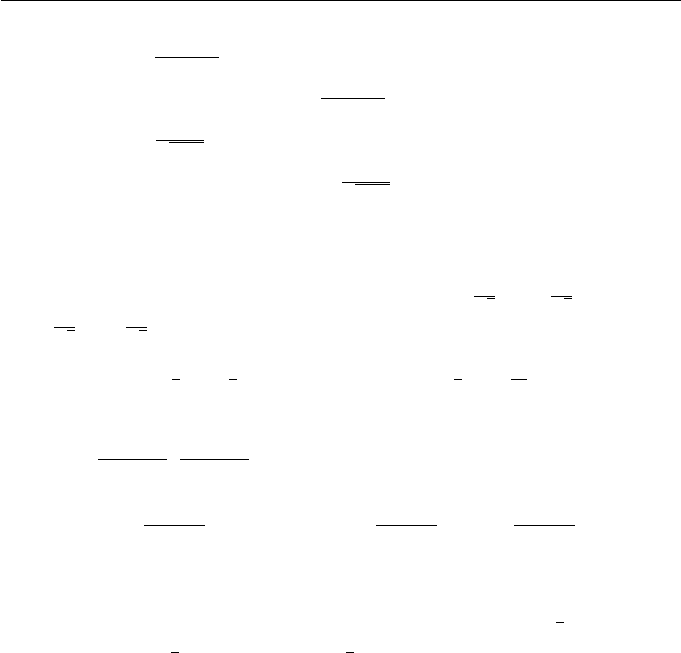
Solutions 333
5.16. (a) n(t)=
1
cosh(t/c)
(−1, sinh (t/c)) .
The offset is (c cosh (t/c) ,t)+
d
cosh(t/c)
(−1, sinh (t/c)).
(b) n(t)=
1
√
1+b
2
(−b sin t − cos t, b cos t − sin t) .
The offset is (e
bt
cos t, e
bt
sin t)+
d
√
1+b
2
(−b sin t − cos t, b cos t − sin t).
5.19. (d) Ellipse, (e) reducible (2x − 3)(x + y − 1) = 0, (f) hyperbola,
(g) hyperbola, (h) reducible (3x +2y)(x − y +2)=0.
5.22. (a) a = 13, b = −5, c = 13, θ = π/4, x =
1
√
2
X
−
1
√
2
Y
and y =
1
√
2
X
+
1
√
2
Y
puts conic in the form 8 (X
+3)
2
+18(Y
+2)
2
−72 = 0.
Applying the translation T(−3, −2) puts the conic in the standard form
for an ellipse
1
9
x
2
+
1
4
y
2
=1.(b)y =6x
2
.(c)
1
4
x
2
−
1
16
y
2
=1.
5.26. (d) (1, −1) and (1/3, −5/3). (e) (2.92, −2.39) and (1.52, −0.28).
5.29. (a)
−2t
1−2t+2t
2
,
−2t
2
1−2t+2t
2
. (c) Consider lines through (1, 0): y = t(x − 1).
x
2
+2x (t(x − 1))−(t(x − 1))
2
−1=(x − 1)
x − t
2
x +2xt + t
2
+1
=0.
Then x =
t
2
+1
t
2
−2t−1
, y = t(x − 1) = t
t
2
+1
t
2
−2t−1
− 1
=
2t+2t
2
t
2
−2t−1
.
5.30. (a) x = t
2
− 1, y = t +2. Then t = y − 2,x=(y − 2)
2
− 1 giving
x − y
2
+4y − 3 = 0. (c) x =2t
2
+ t − 1, y = t
2
− 3t +3. Then
x − 2y =
2t
2
+ t − 1
− 2
t
2
− 3t +3
=7t − 7. So t =
1
7
(x − 2y +7).
Then x =2
1
7
(x − 2y +7)
2
+
1
7
(x − 2y +7)
− 1 which simplifies to
2x
2
− 8xy − 14x +8y
2
− 70y +98=0.
(e)
⎛
⎝
−1 −1 −4
00−3
1 −24
⎞
⎠
has signed minors A
0
= −6, A
1
= −3, A
2
=0,
B
0
= 12, B
1
=0,B
2
= −3, C
0
=3,C
1
= −3, C
2
= 0. Then the implicit
equation is (−3x − 3)
2
− (−6x +12y +3)(−3y) = 0, which simplifies to
x
2
− 2xy +4y
2
+2x + y +1=0.
5.31.
e
1
e
2
e
3
e
4
9 013
3 404
−4 −314
= −16e
1
+55e
2
+ 273e
3
− 43e
4
.
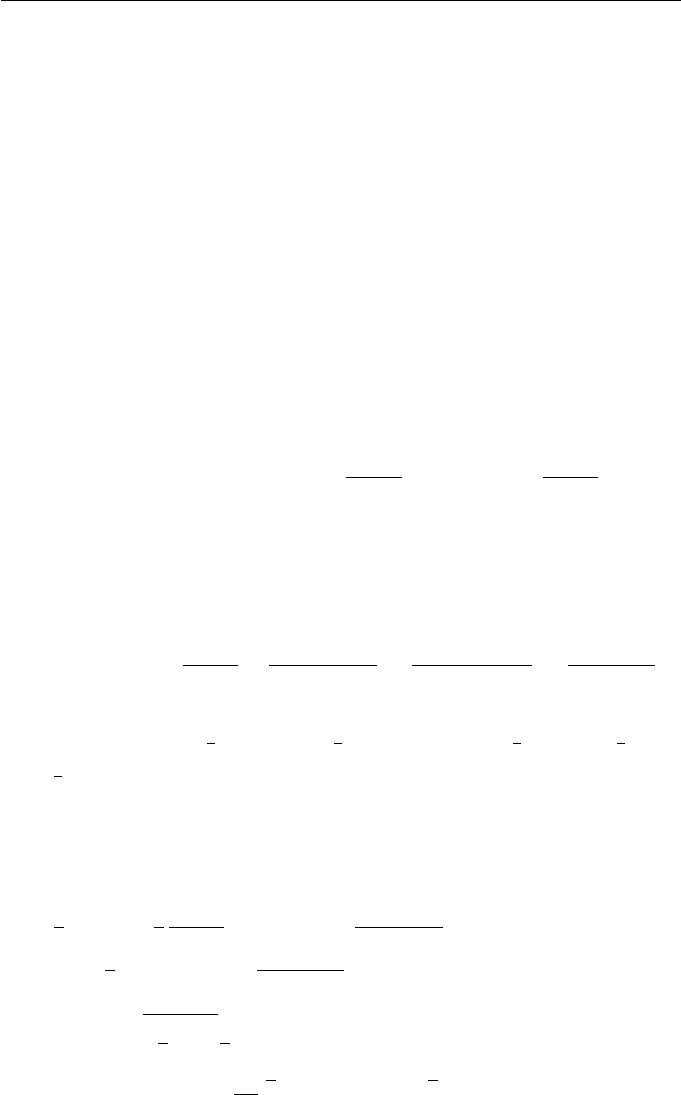
334 Solutions
Chapter 6
6.1. (1 −t)
2
(−1, 5) + 2(1 −t)t(2, 0) + t
2
(4, 6) =
−1+6t − t
2
, 5 − 10t +11t
2
.
B(0.75) = (2. 9375, 3. 6875). B(1.25) is not a point on the curve since
t =1.25 is not in the interval [0, 1].
6.2. (1 − t)
2
(p
0
,q
0
)+2(1− t)t(p
1
,q
1
)+t
2
(p
2
,q
2
)=
(p
0
− 2p
1
+ p
2
) t
2
+2(p
1
− p
0
) t + p
0
,
(q
0
− 2q
1
+ q
2
) t
2
+2(q
1
− q
0
) t + q
0
which is the parametric equation of a parabola.
6.3. B(t)=(1− t)
3
(1, 0) + 3(1 − t)
2
t (2, 3) + 3(1 − t)t
2
(5, 4) + t
3
(2, 1) =
1+3t +6t
2
− 8t
3
, 9t − 6t
2
− 2t
3
. B(0) = (1, 0), B(0.5) = (3.0, 2. 75),
B(1) = (2, 1) .
6.5. (a) b
1
− b
0
and b
1
− b
0
.(b)2b
1
− 2b
0
and 2b
2
− 2b
1
.
6.7. B(t)=(1− t)
3
b
0
+3(1− t)
2
t
2b
0
+b
3
3
+3(1− t)t
2
b
0
+2b
3
3
+ t
3
b
3
.
Expanding gives B(t)=b
0
− b
0
t + tb
3
= b
0
(1 − t)+tb
3
.
6.9. b
0
(2, 2), b
1
(2, 5), b
2
(5, 6), b
3
(8, 6) using endpoint interpolation and
knowledge of the end tangents.
6.10. b
0
(3, 6), b
1
(3, 8), b
2
(4, 9), b
3
(5, 9) using endpoint interpolation and
knowledge of the end tangents.
6.15.
n
i
+
n
i+1
=
n!
i!(n−i)!
+
n!
(i+1)!(n−i−1)!
=
n!(i+1)−n!(n−i)
(i+1)!(n−i)!
=
(n+1)!
(i+1)!(n−i)!
=
n+1
i+1
.
6.16.
1
0
(1−t)
3
dt =
(
−
1
4
(1 − t)
4
)
1
0
=
1
4
,
1
0
3(1−t)
2
tdt=
3
4
t
4
− 2t
3
+
3
2
t
2
1
0
=
1
4
, etc.
6.17. (c) n = 130.
6.19. B
i,n
(1 − t)=
n
i
(1 − (1 − t))
n−i
(1 − t)
i
=
n
i
(1 − t)
i
t
n−i
=
n
n−i
(1 − t)
i
t
n−i
= B
n−i,n
(t).
6.20.
i
n
B
i,n
(t)=
i
n
n!
i!(n−i)!
(1 − t)
n−i
t
i
=
(n−1)!
(i−1)!(n−i)!
(1 − t)
n−i
t
i
so that
n
i=0
i
n
B
i,n
(t)=
n
i=1
(n−1)!
(i−1)!(n−i)!
(1 − t)
n−i
t
i
= t
n−1
i=0
(n−1)!
i!(n−i−1)!
(1 − t)
n−i−1
t
i
= t
n−1
i=0
B
i,n−1
(t)=t.ThenB(t)=
n
i=0
1 −
i
n
a +
i
n
b
B
i,n
(t)=
a
n
i=0
B
i,n
(t) −a
n
i=0
i
n
B
i,n
(t)+b
n
i=0
i
n
B
i,n
(t)=a(1 −t)+bt yield-
ing the line segment
ab.

Solutions 335
6.24. When the control points are collinear the convex hull is a line segment
implying that the B´ezier curve is contained in a line segment.
6.25. (a) b
0
(3, 4), b
1
(5, 5), b
2
(6, 3), b
3
(4, 2). (b) b
0
(0, 0), b
1
(−1, 2), b
2
(1, 3),
b
3
(2, 1). (c) b
0
(0, 0), b
1
(1, 2), b
2
(−1, 3), b
3
(−2, 1).
6.27. b
1
0
(1.5, 0.75), b
1
1
(3.5, 3.5), b
1
2
(5.5, 4.25), b
2
0
(2, 1.4375), b
2
1
(4, 3.6875),
b
3
0
(2.5, 2.0). B(0.25) = (2.5, 2.0).
6.28. (3.456, 1.3776).
6.32. (a) b
1
0
(0.4, 0.1), b
1
1
(1.2, 0.6), b
1
2
(2.2, 0.9), b
2
0
(0.6, 0.225), b
2
1
(1.45, 0.675),
b
3
0
(0.8125, 0.3375). B(0.25) = (0.8125, 0.3375).
(b) B
left
:(0.2, 0.0), (0.4, 0.1), (0.6, 0.225), (0.8125, 0.3375);
B
right
:(0.8125, 0.3375), (1.45, 0.675), (2.2, 0.9), (3.4, 0.0).
6.34. (a) B(1/3) = (0.7, 0.275).
Chapter 7
7.1. b
1
0
(2.6, 6.7, 4.3), b
1
1
(4.3, 6.6, 4.7), b
1
2
(4.4, 7.1, 3.7), b
2
0
(3.11, 6.67, 4.42),
b
2
1
(4.33, 6.75, 4.40), b
3
0
(3.476, 6.694, 4.414). B(0.3) = (3.476, 6.694, 4.414).
7.2. First derivative: 3 ((4, 3) − (6, 3)) = (−6, 0), 3 ((1, 2) − (4, 3)) = (−9, −3),
3((−1, 2) − (1, 2)) = (−6, 0). Second derivative: 2 ((−9, −3) − (−6, 0)) =
(−6, −6).
7.4. n (n − 1) (b
2
− 2b
1
+ b
0
)andn (n − 1) (b
n
− 2b
n−1
+ b
n−2
).
7.5.
B
i,n
(t)=
n
i
i(1 − t)
n−i
t
i−1
−
n
i
(n − i)(1− t)
n−i−1
t
i
= n
n − 1
i − 1
(1 − t)
n−i
t
i−1
− n
n − 1
i
(1 − t)
n−i−1
t
i
= n (B
i−1,n−1
(t) − B
i,n−1
(t)) .
7.7. b
0
(1, 4), b
1
(1, 3), b
2
(0, 5).
7.8. (−3+8t − 6t
2
, −3+4t + t
2
).
7.14. C
0
since c
0
= b
3
=(3, 6). For visual continuity µ3(b
3
− b
2
)=3(−2, 2)
and µ3(c
1
− c
0
)=3(−1, 1). Then take µ =1/2. Change b
2
to (4, 5) to
obtain C
1
.

336 Solutions
7.20. (a)–(c) follow from formulae in the text with w
0
= w
2
=1.
b
0
(1−0.5)
2
+w
1
b
1
2(0.5)(1−0.5)+b
2
(0.5)
2
(1−0.5)
2
+w
1
2(0.5)(1−0.5)+(0.5)
2
=
b
0
+2w
1
b
1
+b
2
2(1+w
1
)
=
1 −
w
1
1+w
1
b
0
+b
2
2
+
w
1
1+w
1
b
1
= S.
7.21. w
0
1
=2.6,w
1
1
=4.2,w
2
1
=2.6,w
0
2
=3.56,w
1
2
=3.24,w
0
3
=3.38, and
b
1
0
(5.769, 4.769), b
1
1
(5.571, 3.857), b
1
2
(4.538, 2.308), b
2
0
(5.629, 4.124),
b
2
1
(5.074, 3.111), b
3
0
(5.309, 3.539) .
7.24. M =
⎛
⎜
⎜
⎝
−33 21 15 3
27 −39 15 3
00−60 0
108 84 60 −48
⎞
⎟
⎟
⎠
. VC =
⎛
⎜
⎜
⎝
−
1
18
0 −
2
9
17
18
0 −
2
9
01 0
−
2
9
0
1
9
⎞
⎟
⎟
⎠
.
⎛
⎜
⎜
⎝
24−22
3/25/24/21/2
−41212 4
0363
⎞
⎟
⎟
⎠
M · VC =
⎛
⎜
⎜
⎝
54 330 −78
−24 −30 −12
−216 −360 −168
135 −135 −135
⎞
⎟
⎟
⎠
.
The projected control points are (−0. 692, −4. 231), (2, 2.5), (1.286, 2.143),
(−1, 1) and weights −78, −12, −168, −135.
7.25. An integral curve is obtained when weights are equal. Rewrite the ex-
pression for the weights w
i
=(n
1
,n
2
,n
3
) ·b
i
v
4
−(n
1
,n
2
,n
3
) ·(v
1
,v
2
,v
3
).
Weights are equal if and only if either (i) v
4
= 0, projection is parallel
and w
i
= −(n
1
,n
2
,n
3
) · (v
1
,v
2
,v
3
) for all i, or (ii) v
4
= 0, projection
is perspective, (n
1
,n
2
,n
3
) · b
i
= 0, and the control points lie in a plane
parallel to the viewplane.
Chapter 8
8.1. B
0
(t)=
5
2
− t +
1
2
(t − 2)
2
b
0
+
−
3
2
+ t − (t − 2)
2
b
1
+
1
2
(t − 2)
2
b
2
for t ∈ [2, 3], B
1
(t)=
7
2
− t +
1
2
(t − 3)
2
b
1
+
−
5
2
+ t − (t − 3)
2
b
2
+
1
2
(t − 3)
2
b
3
for t ∈ [3, 4].
8.2. B
0
(t)=
5
3
−
1
2
t +
1
2
(t − 3)
2
−
1
6
(t − 3)
3
b
0
+
2
3
− (t − 3)
2
+
1
2
(t − 3)
3
b
1
+
−
4
3
+
1
2
t +
1
2
(t − 3)
2
−
1
2
(t − 3)
3
b
2
+
1
6
(t − 3)
3
b
3
for t ∈ [3, 4].
8.3. B
0
(t)=(t − 1)
2
b
0
+
2t −
3
2
t
2
b
1
+
1
2
t
2
b
2
,
B
1
(t)=
3
2
− t +
1
2
(t − 1)
2
b
1
+
−
1
2
+ t − (t − 1)
2
b
2
+
1
2
(t − 1)
2
b
3
,
Solutions 337
B
2
(t)=
5
2
− t +
1
2
(t − 2)
2
b
2
+
−
3
2
+ t −
3
2
(t − 2)
2
b
3
+(t − 2)
2
b
4
.
8.5. B(2.5) = (6.25, −0.25), B(4.2) = (4.28, 4.0).
8.6. b
5
(0, 0), b
6
(2, 0), b
7
(4, 2), t
6
=6,t
7
=7,t
8
=8,t
9
=9,t
10
= 10,
t
11
= 11.
8.12. B(2.5) = (6.25, −0.25), B(4.2) = (4.28, 4.0).
8.13. B(2.4) = (4.04, 2.48).
8.18. B
(2.8) = (0.8022, −3.3045). b
(1)
0
(1.875, 9.375), b
(1)
1
(6.0, 0.0),
b
(1)
2
(1.579, −3.158), b
(1)
3
(−2.857, −4.286).
8.19. b
(1)
0
(4/3, 2), b
(1)
1
(2, −2), b
(1)
2
(2, 4/3), knots 4, 5, 7, 8, 10.
B
(6.2) = (1.733, −0.4), B
(7.4) = (2, −0.667).
8.24.
n
i=0
w
i
N
i,d
(t)
n
j=0
w
j
N
j,d
(t)
=
n
i=0
w
i
N
i,d
(t)
n
j=0
w
j
N
j,d
(t)
=1.
8.27. B
(2.2) = (1.715, −11.853).
8.28. B
(0.5) = (0, −4). B
(0.8) = (7.101, 2.959).
8.31. B(0.65) = (−0.6897, −0.7241).
Chapter 9
9.2. First derivative with respect to s:
p
(1,0)
0,0
=2((4, 3, 1) − (2, 2, 0)) = (4, 2, 2) ,
p
(1,0)
1,0
=2((6, 2, 0) − (4, 3, 1)) = (4, −2, −2) ,
p
(1,0)
0,1
=2((4, 5, 3) − (2, 4, 1)) = (4, 2, 4) , similarly p
(1,0)
1,1
=(4, −4, −4) ,
p
(1,0)
0,2
=(4, 0, 2) , p
(1,0)
1,2
=(4, −2, −2) .
9.4. (a) The tangent vectors at S(0, 0): n (p
1,0
− p
0,0
)andp (p
0,1
− p
0,0
);
S(0, 1): n (p
0,p
− p
0,p−1
)andp (p
1,p
− p
0,p
); S(1, 0): n (p
n,0
− p
n−1,0
)
and p (p
n,1
− p
n,0
); S(1, 1): n (p
n,p
− p
n−1,p
)andp (p
n,p
− p
n,p−1
). (b)
The normal at S(0, 0) is np (p
1,0
− p
0,0
) × (p
0,1
− p
0,0
);
at S(0, 1) is np (p
0,p
− p
0,p−1
) × (p
1,p
− p
0,p
) etc.
9.5. (All the points listed in the order p
0,0
, p
1,0
, etc.)
(2, 0, 1), (1, 0, 2), (3, 0, 3), (1, 0, 4), (1, 0, 5);
(2, 2, 1), (1, 1, 2), (3, 3, 3), (1, 1, 4), (1, 1, 5);

338 Solutions
(−2, 2, 1), (−1, 1, 2), (−3, 3, 3), (−1, 1, 4), (−1, 1, 5);
(−2, 0, 1), (−1, 0, 2), (−3, 0, 3), (−1, 0, 4), (−1, 0, 5);
(−2, −2, 1), (−1, −1, 2), (−3, −3, 3), (−1, −1, 4), (−1, −1, 5);
(2, −2, 1), (1, −1, 2), (3, −3, 3), (1, −1, 4), (1, −1, 5);
(2, 0, 1), (1, 0, 2), (3, 0, 3), (1, 0, 4), (1, 0, 5).
9.6. b
0,0
(2, 3, 0), b
1,0
(1, 5, 2), b
2,0
(1, 7, −1), b
3,0
(2, 9, −3), b
0,1
(4, 7, −4),
b
1,1
(3, 9, −2), b
2,1
(3, 11, −5), b
3,1
(4, 13, −7).
9.7. Control points as for Exercise 9.6, weights w
0,0
= w
0,1
=1,w
1,0
= w
1,1
=
2,w
2,0
= w
2,1
=3,w
3,0
= w
3,1
=1.
9.9. b
0,0
(0, 0, 0), b
1,0
(0,a,0), b
2,0
(a, 2a, 0), b
0,1
(0, 0, 1), b
1,1
(0,a,1),
b
2,1
(a, 2a, 1). Parabolic cylinder can be obtain by sweeping a line seg-
ment along a quadratic B´ezier curve.
9.10. NURBS sphere has control points: (Listed in the order p
0,0
, p
1,0
, etc)
(1, 0, 0), (1, 0, 1), (−1, 0, 1), (−1, 0, 0), (−1, 0, −1), (1, 0, −1), (1, 0, 0);
(1, 1, 0), (1, 1, 1), (−1, −1, 1), (−1, −1, 0), (−1, −1, −1), (1, 1, −1),
(1, 1, 0);
(−1, 1, 0), (−1, 1, 1), (1, −1, 1), (1, −1, 0), (1, −1, −1), (−1, 1, −1),
(−1, 1, 0);
(−1, 0, 0), (−1, 0, 1), (1, 0, 1), (1, 0, 0), (1, 0, −1), (−1, 0, −1), (−1, 0, 0);
(−1, −1, 0), (−1, −1, 1), (1, 1, 1), (1, 1, 0), (1, 1, −1), (−1, −1, −1),
(−1, −1, 0);
(1, −1, 0), (1, −1, 1), (−1, 1, 1), (−1, 1, 0), (−1, 1, −1), (1, −1, −1),
(1, −1, 0);
(1, 0, 0), (1, 0, 1), (−1, 0, 1), (−1, 0, 0), (−1, 0, −1), (1, 0, −1), (1, 0, 0).
Weights: w
i,0
= {1, 0.5, 0.5, 1, 0.5, 0.5, 1},
w
i,1
= w
i,2
= {0.5, 0.25, 0.25, 0.5, 0.25, 0.25, 0.5},
w
i,3
= {1, 0.5, 0.5, 1, 0.5, 0.5, 1},
w
i,4
= w
i,5
= {0.5, 0.25, 0.25, 0.5, 0.25, 0.25, 0.5},
w
i,6
= {1, 0.5, 0.5, 1, 0.5, 0.5, 1}.
Knots for s and t 0, 0, 0, 0.25, 0.5, 0.5, 0.75, 1, 1, 1.
