Marsh D. Applied Geometry for Computer Graphics and CAD
Подождите немного. Документ загружается.


278 Applied Geometry for Computer Graphics and CAD
Further,
b = t × n =
t
2
2+t
2
, −
2t
2+t
2
,
2
2+t
2
.
The curvature is
κ =
˙
t
/ν =
4
(2 + t
2
)
2
.
Further,
n ·
˙
b =
−
2t
2+t
2
,
2 − t
2
2+t
2
,
2t
2+t
2
·
4t
(2 + t
2
)
2
, −
4 − 2t
2
(2 + t
2
)
2
, −
4t
(2 + t
2
)
2
= −
2
2+t
2
.
Thus, the torsion is
τ = −
n ·
˙
b
ν =
4
(2 + t
2
)
2
.
EXERCISES
10.8. Show that
¨
C =˙νt + κν
2
n and
...
C
=
¨ν − κ
2
ν
3
t +
3κν ˙ν +˙κν
2
n +
κτν
3
b.
10.9. Show that for a unit speed curve C(s), κ(s)=|C
(s)|.
10.10. Determine the Frenet frame, curvature, and torsion of the curve
C(t)=(4cost, 5 − 5sint, −3cost). Describe the curve.
10.11. Determine the Frenet frame, curvature, and torsion of the curve
C(t)=
3cost − 4sint, 3sint +4cost, 5
√
3t
.
The next theorem gives one of the most direct methods of computing the
curvature, torsion, and Frenet frame. In particular, the curvature and torsion
can be obtained without having to compute the Frenet frame.
Theorem 10.9
Let C be a regular curve. Then
κ =
|
˙
C×
¨
C
|
|
˙
C
|
3
,τ=
(
˙
C×
¨
C
)
·
...
C
|
˙
C×
¨
C
|
2
, t =
˙
C
|
˙
C
|
, b =
˙
C×
¨
C
|
˙
C×
¨
C
|
, n = b × t .

10. Curve and Surface Curvatures 279
Proof
Using
˙
C = νt and the results of Exercise 10.8,
˙
C ×
¨
C = νt ×
˙νt + κν
2
n
= ν ˙ν (t × t)+κν
3
(t × n) .
Then, since t × t = 0 and t × n = b it follows that
˙
C ×
¨
C = κν
3
b . (10.20)
Hence
˙
C ×
¨
C
=
κν
3
b
= κν
3
,sothat
κ =
|
˙
C×
¨
C
|
ν
3
=
|
˙
C×
¨
C
|
|
˙
C
|
3
and b =
˙
C×
¨
C
|
˙
C×
¨
C
|
.
Equation (10.12) gives t =
˙
C
˙
C
, and it follows that n = b × t. Equations
(10.20) and (10.14), and Exercise 10.8, imply
˙
C ×
¨
C
·
...
C
=
κν
3
b
·
¨ν − κ
2
ν
3
t +
3κν ˙ν +˙κν
2
n + κτν
3
b
= κ
2
τν
6
.
Hence,
τ =
(
˙
C×
¨
C
)
·
...
C
κ
2
ν
6
=
(
˙
C×
¨
C
)
·
...
C
|
˙
C×
¨
C
|
2
.
Example 10.10
Consider the helix C(t)=
a cos
t
c
,asin
t
c
,
bt
c
where c =(a
2
+ b
2
)
1/2
and
a>0. Then
˙
C =
−
a
c
sin
t
c
,
a
c
cos
t
c
,
b
c
,
¨
C =
−
a
c
2
cos
t
c
, −
a
c
2
sin
t
c
, 0
,
...
C
=
a
c
3
sin
t
c
, −
a
c
3
cos
t
c
, 0
. The curve is unit speed since
˙
C
=
−
a
c
sin
t
c
2
+
a
c
cos
t
c
2
+
bt
c
2
=1.
Then
˙
C ×
¨
C =
b
c
3
a sin
t
c
, −
b
c
3
a cos
t
c
,
a
2
c
3
and
˙
C ×
¨
C
=
a
a
2
+b
2
. Hence
κ =
|
˙
C×
¨
C
|
|
˙
C
|
3
=
a
a
2
+ b
2
.
(Since the curve is unit speed the curvature can also be computed using κ =
|t
| =
¨
C
.) Further,
˙
C ×
¨
C
·
...
C
=
a
2
b
(a
2
+b
2
)
3
, and hence
τ =
(
˙
C×
¨
C
)
·
...
C
|
˙
C×
¨
C
|
2
=
b
a
2
+ b
2
.

280 Applied Geometry for Computer Graphics and CAD
The Frenet frame is
t =
˙
C
˙
C
=
−
a
c
sin
t
c
,
a
c
cos
t
c
,
b
c
,
b =
˙
C ×
¨
C
˙
C ×
¨
C
=
b
c
sin
t
c
, −
b
c
cos
t
c
,
a
c
,
n = b × t =
−cos
t
c
, −sin
t
c
, 0
.
Example 10.11
Consider the curve C(t)=
t,
1
2
t
2
,
1
6
t
3
.Then
˙
C =
1,t,
1
2
t
2
,
¨
C =(0, 1,t), and
...
C
=(0, 0, 1). Then ν =
˙
C
=
2+t
2
2
,and
˙
C ×
¨
C
=
1,t,
1
2
t
2
× (0, 1,t)
=
1
2
t
2
, −t, 1
=
2+t
2
2
.
Hence
κ =
|
˙
C×
¨
C
|
|
˙
C
|
3
=
4
(2+t
2
)
2
.
Further,
˙
C ×
¨
C
·
...
C
=
1
2
t
2
, −t, 1
· (0, 0, 1) = 1. So
τ =
(
˙
C×
¨
C
)
·
...
C
|
˙
C×
¨
C
|
2
=
4
(2+t
2
)
2
.
Example 10.12 (Application to Rigid Body Motion)
Consider the motion of a rigid body. Suppose that a reference point on the
body moves along a unit speed curve C(s). Instantaneously, a line of points of
the rigid body are stationary, and the body rotates about that line. The line
has the direction of the Darboux vector ω which satisfies
t
= ω × t, n
= ω × n, b
= ω × b .
The magnitude ω of ω is the angular velocity of the motion at that instant.
Suppose the orthonormal expansion of ω with respect to the Frenet frame is
ω = αt + βn + γb.Then
t
=(αt + βn + γb) × t =γn − βb
n
=(αt + βn + γb) × n = −γt+αb
b
=(αt + βn + γb) × b =βt − αn
and the Frenet formulae give α = τ , β =0,andγ = κ. Hence ω = τt+κb.

10. Curve and Surface Curvatures 281
Theorem 10.13
Let C(t) be a regular curve, defined on an interval I, with curvature κ(t)and
torsion τ(t).
1. If κ(t) = 0 for all t ∈ I,thenC(t) is a line segment.
2. If τ(t)=0andκ(t) = 0 for all t ∈ I,thenC(t) is a planar curve.
3. If τ (t) = 0 for all t ∈ I,andκ is a non-zero constant, then C(t)isanarc
of a circle of radius 1/κ.
Proof
Reparametrize the curve so that the curve is unit speed.
1. Since t
= κn, the assumption κ = 0 implies that t
= 0.Thust is a
constant vector and
(C × t)
=(C
× t)+(C × t
)=(t × t)+(C × 0)=0 .
Hence C × t = v for some constant vector v. The identity imposes two
independent linear constraints on the points of C, and hence the curve is
a line.
2. Since b
= τn, the assumption τ = 0 implies that b
= 0.Thusb is a
constant vector (non-zero since κ =0).Then
(C · b)
=(C
· b)+(C · b
)=(t · b)+(C · 0)=0 .
Hence C · b = α for some constant α, and therefore C is planar.
3. Since τ = 0, the curve is planar and it is sufficient to show that every point
of C has a constant distance from a fixed point. Since n
= −κt+τb = −κt
and 1/κ is constant,
C+
1
κ
n
= C
+
1
κ
n
= t+
1
κ
(−κt)=0 .
Hence C+1/κn = v for some constant vector v.Then|C − v| =1/ |κ|
implying every point of the curve has a constant distance 1/ |κ| from v.
The discussion on curvature of space curves is concluded with two theorems
(without proofs) which are generalizations of Theorem 10.3 to space curves.

282 Applied Geometry for Computer Graphics and CAD
Theorem 10.14
Let κ(s) > 0andτ (s) be continuous functions. Then there exists a curve for
which s is the arclength parameter, and κ and τ are the curvature and torsion
functions.
Theorem 10.15
Any two space curves, parametrized with respect to arclength, with identical
curvature κ(s) and torsion τ(s) functions, differ only by a translation and
rotation. If two space curves have the same curvature function κ(s), but have
torsion functions of opposite sign, they differ only by a translation, a rotation,
and a reflection.
EXERCISES
10.12. Determine the curvature and torsion of the curve
C(t) = (5 cos t, 3cost−4sint, 4cost+3sint). Deduce that the curve
is planar, and identify the type of curve.
10.13. Determine the curvature and torsion of the following curves:
(a) C(t)=
3t − t
3
, 3t
2
, 3t + t
3
;
(b) C(t)=((t +sint) , (1 − cos t) ,t);
(c) C(t)=
t,
1
t
+1,
1
t
− t
;
(d) C(t)=(1− cos(t),t− sin(t), 4 sin(t/2)).
10.14. Determine the Frenet frame, curvature, and torsion of the curve
C(t)=
1
√
2
t,
1
3
(1 + t)
3/2
,
1
3
(1 − t)
3/2
, t ∈ (−1, 1).
10.15. Show that the Darboux vector satisfies t
× t
= κ
2
ω.
10.16. Let C : R → R
n
be a smooth function at t = t
0
. Then Taylor’s
theorem gives
C(t)=C(t
0
)+(t−t
0
)
˙
C(t
0
)+
1
2
(t−t
0
)
2
¨
C(t
0
)+
1
6
(t−t
0
)
3
...
C
(t
0
)+··· .
(a) Apply the formulae which express the derivatives
˙
C,
¨
C,
...
C
in
terms of the Frenet frame to give the Frenet approximation of

10. Curve and Surface Curvatures 283
C(t) of the form
C(t
0
)+t
0
(t − t
0
)ν
0
+
1
2
(t − t
0
)
2
˙ν
0
+
1
6
(t − t
0
)
3
¨ν
0
− κ
2
0
ν
3
0
+ ···
+ n
0
1
2
(t − t
0
)
2
κ
0
ν
2
0
+
1
6
(t − t
0
)
3
3κ
0
ν
0
˙ν
0
+˙κ
0
ν
2
0
+ ···
+ b
0
1
6
(t − t
0
)
3
κτ
0
ν
3
0
+ ···
(10.21)
where ν
0
,˙ν
0
,¨ν
0
, κ
0
, τ
0
denote the speed, the derivatives of speed,
the curvature, and the torsion at the point C(t
0
).
(b) Suppose C(t
0
) is the origin. Show that the orthographic pro-
jections of the curve onto the osculating, rectifying and normal
planes are approximated by the following curves:
(i)
(t − t
0
)ν
0
,
1
2
(t − t
0
)
2
κ
0
ν
2
0
, i.e. y =
1
2
κ
0
x
2
,
(ii)
(t − t
0
)ν
0
,
1
6
(t − t
0
)
3
κ
0
τ
0
ν
3
0
, i.e. z =
1
6
κ
0
τ
0
x
3
,and
(iii)
1
2
(t − t
0
)
2
κ
0
ν
2
0
,
1
6
(t − t
0
)
3
κ
0
τ
0
ν
3
0
, i.e. z
2
=
2τ
2
0
9κ
0
x
3
, respec-
tively.
10.3 Curvature of B´ezier Curves
Theorem 10.16
The curvature and torsion of a B´ezier curve B(t)att =0are
κ =
n − 1
n
b
a
3
,τ=
n − 2
n
c
b
2
where a = |b
1
− b
0
|, b = |(b
1
− b
0
) × (b
2
− b
1
)|,and
c =((b
1
− b
0
) × (b
2
− b
1
)) · (b
3
− b
2
) .
Proof
The derivatives of B(t) are obtained using Theorem 7.3 and its corollaries,
˙
B(0) = n (b
1
− b
0
) ,
¨
B(0) = n (n − 1) (b
2
− 2b
1
+ b
0
)=n (n − 1) ((b
2
− b
1
) − (b
1
− b
0
)) ,
...
B
(0) = n (n − 1) (n − 2) (b
3
− 3b
2
+3b
1
− b
0
) .

284 Applied Geometry for Computer Graphics and CAD
Then,
˙
B
= n |b
1
− b
0
| ,
˙
B ×
¨
B
= n
2
(n − 1) |(b
1
− b
0
) × ((b
2
− b
1
) − (b
1
− b
0
))|
= n
2
(n − 1) |(b
1
− b
0
) × (b
2
− b
1
)| ,
and
κ =
|
˙
B×
¨
B
|
|
˙
B
|
3
=
(n − 1) |(b
1
− b
0
) × (b
2
− b
1
)|
n |b
1
− b
0
|
3
.
Further,
˙
B ×
¨
B
·
...
B
= n
3
(n − 1)
2
(n − 2) ((b
1
− b
0
) × (b
2
− b
1
)) · (b
3
− 3b
2
+3b
1
− b
0
) .
Expressing b
3
−3b
2
+3b
1
−b
0
=(b
3
− b
2
)−(b
2
− b
1
)−(b
2
− b
1
)+(b
1
− b
0
)
in the previous equation, expanding the cross product, and simplifying gives
˙
B ×
¨
B
·
...
B
= n
3
(n − 1)
2
(n − 2) ((b
1
− b
0
) × (b
2
− b
1
)) · (b
3
− b
2
) .
Hence
τ =
(
˙
B×
¨
B
)
·
...
B
|
˙
B×
¨
B
|
2
=
(n − 2) (((b
1
− b
0
) × (b
2
− b
1
)) · (b
3
− b
2
))
n |(b
1
− b
0
) × (b
2
− b
1
)|
2
.
The reader is left the exercise of proving the next theorem.
Theorem 10.17
The curvature and torsion of a rational B´ezier curve B(t)att =0are
κ =
n − 1
n
w
0
w
2
w
2
1
b
a
2
,τ=
n − 2
n
w
0
w
3
w
1
w
2
c
b
2
where a, b,andc are as above.
The curvature and torsion of an integral or rational B´ezier curve B(t)at
the point B(t
0
), t
0
∈ [0, 1] can be computed by applying the integral or rational
de Casteljau algorithm to subdivide the curve at t = t
0
into the two segments
B
left
(t)andB
right
(t). Applying Theorem 10.16 or 10.17 to B
right
(t)att =0
gives the curvature and torsion at B(t
0
).

10. Curve and Surface Curvatures 285
Example 10.18
Consider the cubic B´ezier curve B(t) with control points b
0
(0, 1, 4), b
1
(2, −1, 3),
b
2
(3, 2, 7), b
3
(5, 2, 2). Then
a = |(2, −1, 3) − (0, 1, 4)| =3,
b = |((2, −1, 3) − (0, 1, 4)) × ((3, 2, 7) − (2, −1, 3))| = |(−5, −9, 8)| =
√
170 ,
c =(−5, −9, 8) · ((5, 2, 2) − (3, 2, 7)) = −50 .
Hence the curvature and torsion of B(t)atB(0) are κ(0) =
3−1
3
√
170
(3)
3
=
2
81
√
170,
and τ(0) =
3−2
3
−50
170
= −
5
51
.
EXERCISES
10.17. Determine the curvature and torsion of the cubic B´ezier curve with
control points b
0
(1, 2, 1), b
1
(3, 0, 4), b
2
(6, −3, 2), and b
3
(4, 2, 3)
(a) at the point B(0), and
(b) at the point B(0.3). (Hint: Example 7.1 may help!)
10.18. Determine the curvature of the cubic rational B´ezier curve with con-
trol points b
0
(3, 2, 7), b
1
(5, 4, 3), b
2
(8, 3, 3), b
3
(5, 2, 4), and weights
1, 2, 2, 1 at the points B(0) and B(0.6).
10.19. Determine the control points of the planar B´ezier curve B(t)of
degree 5 satisfying B(0) = (0, 0), B(1) = (5, 0), B
(0) = (1, 4),
B
(1) = (−1, 2), κ(0) = 1, and κ(1) = 2.
10.20. Determine expressions for the Frenet frame t, n, b of a B´ezier curve
B(t)att =0.
10.21. Prove Theorem 10.17.
10.4 Surface Curvatures
In this section surfaces are parametrized using the variables u and v (s and t
were used in the chapter on surfaces). Let U be an open or closed subset of
R
2
and let S : U → R
3
, be a parametrized surface with unit normal N(u, v).
If (u(t),v(t)) is a regular curve in U,thenitismappedbyS to the curve
C(t)=S(u(t),v(t)) on the surface. The chain rule gives
˙
C =˙uS
u
+˙vS
v
and
˙
C ·N =(˙uS
u
+˙vS
v
) ·N =˙u (S
u
· N)+ ˙v (S
v
· N) = 0. So every tangent vector

286 Applied Geometry for Computer Graphics and CAD
to the curve C is a tangent vector to the surface. The converse, that every
tangent vector of the surface is a tangent vector to some curve on the surface,
is proved in the following lemma.
Lemma 10.19
Let S : U → R
3
be a regular surface. If v is a tangent vector to the surface at
apointp then there exists a curve C(t), t ∈ (−a, a)(somea>0), such that
C(0) = p and
˙
C(0) = v.
Proof
Since S is regular, S
u
and S
v
are linearly independent vectors, and therefore v =
αS
u
(u, v)+βS
v
(u, v)forsomeα and β.LetC(t)=S(u+αt, v+βt) be defined on
(−a, a)wherea>0 is chosen so that (−a, a) is contained in U.ThenC(0) = p,
and the chain rule yields
˙
C(t)=αS
u
(u + αt, v + βt)+βS
v
(u + αt, v + βt)and
˙
C(0) = αS
u
(u, v)+βS
v
(u, v)=v.
In view of the lemma, the tangent vectors at a point p will often be expressed
in the form ˙uS
u
+˙vS
v
.
Suppose p = S(u, v) is a regular point, and let v be a tangent vector to the
surface at p. The plane through p containing the directions v and N intersects
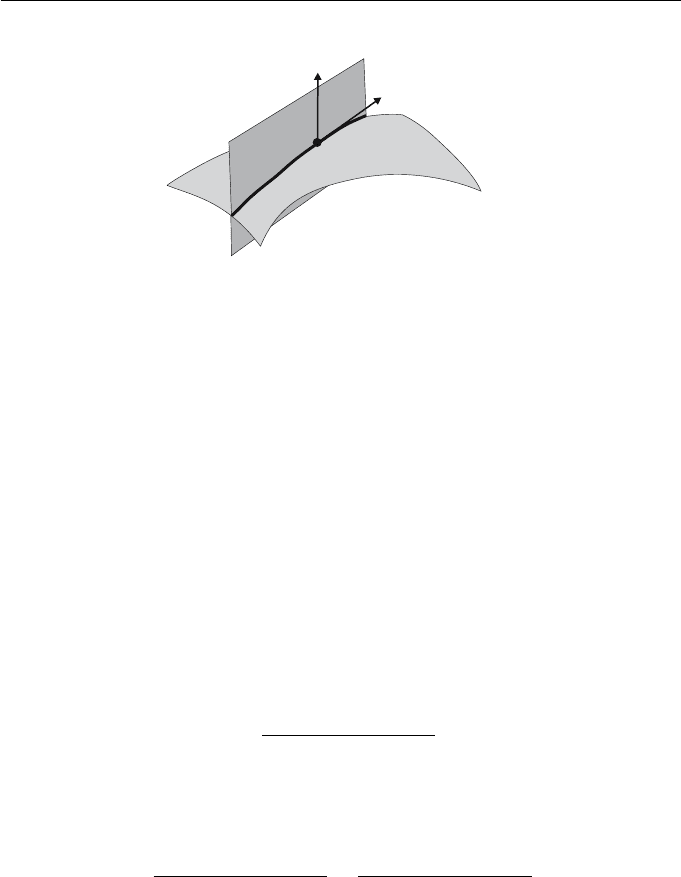
S in a curve C(t) as shown in Figure 10.5. The curve can be parametrized so
that C(0) = p and
˙
C(0) = v. The curvature κ(t)ofC(t)att = 0 is called the
normal curvature of S in the direction v at p, and denoted κ
p
(v). Theorem
10.21 will prove that κ
p
(v) has a maximum and a minimum value, denoted
κ
max
and κ
min
respectively, called the principal curvatures. The tangent vectors
which give rise to the principal curvatures are called the principal directions.
AcurveC(t)onS for which every tangent vector
˙
C(t) is a principal direction
of the surface is called a line of principal curvature.
Let C(t)=S(u(t),v(t)) be a curve on S with unit tangent t and unit normal
n.Then
˙
C = νt,
¨
C =˙νt+ν
2
κn and
¨
C · N =
˙νt+ν
2
κn
·N =ν
2
κn · N . (10.22)
The chain rule applied to C(t)=S(u(t),v(t)) gives
˙
C =˙uS
u
+˙vS
v
,
¨
C =˙u (˙uS
uu
+˙vS
vu
)+¨uS
u
+˙v (˙uS
uv
+˙vS
vv
)+¨vS
v
=˙u
2
S
uu
+2˙u ˙vS
uv
+˙v
2
S
vv
+¨uS
u
+¨vS
v
.
10. Curve and Surface Curvatures 287
v
N
C()t
C()t
p
S
Figure 10.5
Let E = S
u
· S
u
, F = S
u
· S
v
,andG = S
v
· S
v
,then
ν
2
=
˙
C ·
˙
C =(˙uS
u
+˙vS
v
) · (˙uS
u
+˙vS
v
)
=˙u
2
S
u
· S
u
+2˙u ˙vS
u
· S
v
+˙v
2
S
v
· S
v
= E ˙u
2
+2F ˙u ˙v + G ˙v
2
.
Further, let L = S
uu
·N, M = S
uv
·N,andN = S
vv
·N,then
¨
C · N =
˙u
2
S
uu
+2˙u ˙vS
uv
+˙v
2
S
vv
+¨uS
u
+¨vS
v
· N
=˙u
2
S
uu
· N +2˙u ˙vS
uv
· N +˙v
2
S
vv
· N
= L ˙u
2
+2M ˙u ˙v + N ˙v
2
. (10.23)
The expressions E ˙u
2
+2F ˙u ˙v + G ˙v
2
and L ˙u
2
+2M ˙u ˙v + N ˙v
2
are called the first
and second fundamental forms of the surface. Equations (10.22) and (10.23)
give the curvature κ of C at p
κ=
L ˙u
2
+2M ˙u ˙v + N ˙v
2
ν
2
n · N
.
Suppose C is a curve, through the point p, in the plane containing the unit
normal N to the surface at p. Then n · N = 1 and the formula yields the normal
curvature of the surface in the direction v =
˙
C
κ
p
(
˙
C)=
L ˙u
2
+2M ˙u ˙v + N ˙v
2
ν
2
=
L ˙u
2
+2M ˙u ˙v + N ˙v
2
E ˙u
2
+2F ˙u ˙v + G ˙v
2
. (10.24)
The sign of κ
p
indicates whether, near p, the curve (and the surface in the
direction v) is bending towards or away from the normal, as illustrated in
Figure 10.6.
Example 10.20
Consider the surface S(u, v)=(u, v, u
2
− v
2
). Then S
u
=(1, 0, 2u), S
v
=
(0, 1, −2v), S
uu
=(0, 0, 2), S
uv
=(0, 0, 0), S
vv
=(0, 0, −2), S
u
× S
v
=
