Marsh D. Applied Geometry for Computer Graphics and CAD
Подождите немного. Документ загружается.

288 Applied Geometry for Computer Graphics and CAD
S
C()t
C()t
p
N
v
S
C()t
C()t
p
N
v
k
p
>0
k
p
> 0
k
p
<0
k
p
< 0
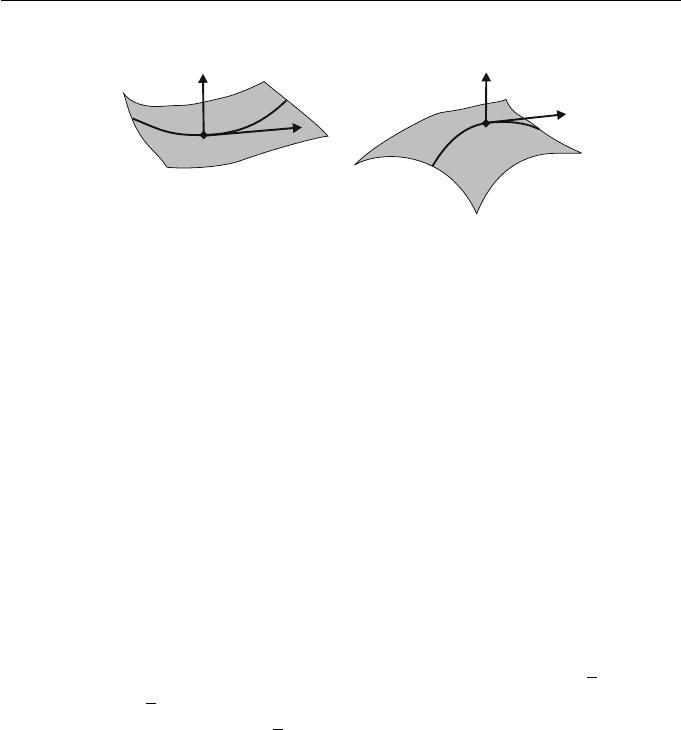
Figure 10.6 Geometric interpretation of the sign of the normal curvature
(−2u, 2v, 1),
N =(−2u, 2v,1) / |(−2u, 2v,1)| =
1+4u
2
+4v
2
−1/2
(−2u, 2v, 1) ,
E = S
u
· S
u
=1+4u
2
, F = S
u
· S
v
= −4uv, G = S
v
· S
v
=1+4v
2
,
L = S
uu
· N =2/
1+4u
2
+4v
2
1/2
, M = S
uv
· N =0,N = S
vv
· N =
−2/
1+4u
2
+4v
2
1/2
.Thecurve(u(t),v(t)) = (t, t
2
)ismappedbyS to the
surface curve C(t)=S(t, t
2
)=(t, t
2
,t
2
− t
4
). Then ˙u(t)=1and ˙v(t)=2t.
At t = 0 the curve passes through the origin and has tangent vector
˙
C(0) =
(1, 0, 0), u = v =0, ˙u =1, ˙v =0,E =1,F =0,G =1,L =2,M =0,and
N = −2. Hence, the normal curvature at the origin in the direction (1, 0, 0) is
κ
p
(1, 0, 0) = 2.
The curve (u(t),v(t)) = (cos t, sin t) is mapped to the surface curve C(t)=
(cos t, sin t, cos
2
t−sin
2
t). Then ˙u(t)=−sin t,˙v(t)=cost.Att = π/2thecurve
passes through the point (0, 1, −1) and has tangent vector
˙
C(π/2) = (−1, 0, 0),
u =0,v =1, ˙u = −1, ˙v =0,E =1,F =0,G =5,L =2/
√
5, M =0,
and N = −2/
√
5. Hence the normal curvature at (0, 1, −1) in the direction
(−1, 0, 0) is κ
p
(−1, 0, 0) = 2/
√
5.
Theorem 10.21 (Euler)
Let p be a regular point of a surface S(u, v). Suppose the normal curvature
κ
p
(v) is a non-constant function of v. Then there are unique unit tangent
vectors v
max
and v
min
such that the normal curvature κ
p
(v
max
)=κ
max
is
maximal, and κ
p
(v
min
)=κ
min
is minimal. Further, v
max
and v
min
are perpen-
dicular.
Proof
The surface curve
˙
C(t)=S(u(t),v(t)) has tangent vector
˙
C =˙uS
u
+˙vS
v
,and

10. Curve and Surface Curvatures 289
by (10.24) the normal curvature in this direction is
κ
p
(˙uS
u
+˙vS
v
)=
L ˙u
2
+2M ˙u ˙v + N ˙v
2
E ˙u
2
+2F ˙u ˙v + G ˙v
2
. (10.25)
The maximum and minimum normal curvatures are the extrema of (10.25)
for all tangent vectors ˙uS
u
+˙vS
v
. By reparametrizing (u(t),v(t)), the tangent
vectors ˙uS
u
+˙vS
v
can be assumed to have unit length. Then E ˙u
2
+2F ˙u ˙v +
G ˙v
2
=(˙uS
u
+˙vS
v
) · (˙uS
u
+˙vS
v
) = 1. Therefore the problem is to find the
extrema of κ
p
(˙uS
u
+˙vS
v
)=L ˙u
2
+2M ˙u ˙v + N ˙v
2
subject to the constraint
E ˙u
2
+2F ˙u ˙v + G ˙v
2
= 1. The solution can be found by applying the method of
Lagrange multipliers (treating ˙u and ˙v as variables). Let
L(˙u, ˙v)=L ˙u
2
+2M ˙u ˙v + N ˙v
2
− λ
E ˙u
2
+2F ˙u ˙v + G ˙v
2
− 1
.
The conditions for the extrema are
∂L
∂ ˙u
=2L ˙u +2M ˙v −2λ (2E ˙u +2F ˙v)=0,
∂L
∂ ˙v
=2M ˙u +2N ˙v − 2λ (2G ˙v +2F ˙u)=0,
giving
(L − λE)˙u +(M − λF )˙v =0, (10.26)
(M − λF )˙u +(N − λG)˙v =0, (10.27)
which can be expressed in the matrix form
(S − λF)
˙u
˙v
=0, (10.28)
where
F =
EF
FG
and S =
LM
MN
.
F and S are called the first and second fundamental matrices, respectively. Since
EG−F
2
= 0 at a regular point (Exercise 10.22), F is non-singular and (10.28)
gives
F
−1
S − λI
˙u
˙v
=0.
Solving (10.28) for λ is equivalent to solving for the eigenvalues of F
−1
S.The
eigenvalues λ satisfy
0=
˙u ˙v
(S − λF)
˙u
˙v
=
˙u ˙v
S
˙u
˙v
− λ
˙u ˙v
F
˙u
˙v
= L ˙u
2
+2M ˙u ˙v + N ˙v
2
− λ
E ˙u
2
+2F ˙u ˙v + G ˙v
2
.
290 Applied Geometry for Computer Graphics and CAD
Hence
λ =
L ˙u
2
+2M ˙u ˙v + N ˙v
2
E ˙u
2
+2F ˙u ˙v + G ˙v
2
.
Thus the eigenvalues of F
−1
S are the principal curvatures κ
max
and κ
min
,and
the corresponding principal directions w
1
=
˙u
1
˙v
1
and w
2
=
˙u
2
˙v
2
yield the principal
directions v
max
=˙u
1
S
u
+˙v
1
S
v
and v
min
=˙u
2
S
u
+˙v
2
S
v
.
Then (10.28) implies (S − Fκ
max
) w
1
= 0, and the fact that F and S are
symmetric gives
w
T
1
(S − Fκ
max
)
T
= w
T
1
S
T
− F
T
κ
max
= w
T
1
(S − Fκ
max
)=0.
So w
T
1
S = w
T
1
Fκ
max
and multiplying on the right by w
2
gives
w
T
1
Sw
2
= κ
max
w
T
1
Fw
2
. (10.29)
Further, (10.28) implies (F − Sκ
min
) w
2
=0,so
w
T
1
Sw
2
= κ
min
w
T
1
Fw
2
. (10.30)
Then subtracting Equation (10.30) from (10.29) gives (κ
max
− κ
min
) w
T
1
Fw
2
=
0, and since κ
max
= κ
min
it follows that w
T
1
Fw
2
= 0. Further, since
w
T
1
Fw
2
=(˙u
1
S
u
+˙v
1
S
v
) · (˙u
2
S
u
+˙v
2
S
v
)
= v
max
· v
min
=0
it follows that v
max
and v
min
are perpendicular.
Eliminating λ from Equations (10.26) and (10.27) gives
(EM − FL)˙u
2
+(EN − GL)˙u ˙v +(FN − GM )˙v
2
=0. (10.31)
Equation (10.31) is a necessary and sufficient condition for a curve S(u(t),v(t))
to be a line of curvature. In particular, the u-parameter curve (u(t),v(t)) =
(t, v
0
), for which ( ˙u(t), ˙v(t)) = (1, 0), is a line of curvature if and only if EM −
FL = 0. Likewise, the v-parameter curve is a line of curvature if and only if
FN−GM =0.SinceEG−F
2
= 0, the conditions EM −FL = FN−GM =0
can be satisfied if and only F = M = 0. Therefore the parameter curves are
the lines of curvature if and only if F = M =0.
Let v =˙uS
u
+˙vS
v
and w =
˙u
˙v
. The formula for normal curvature (10.25)
can be expressed in terms of the fundamental matrices
κ
p
(v)=
w
T
Sw
w
T
Fw
.
A second theorem due to Euler states that the normal curvature κ
p
(v)inan
arbitrary direction v can be obtained from the principal curvatures [8].

10. Curve and Surface Curvatures 291
Theorem 10.22 (Euler)
If θ is the angle between a tangent vector v and v
max
,then
κ
p
(v)=κ
max
cos
2
θ + κ
min
sin
2
θ.
The curvatures of a surface most commonly used are not the principal
curvatures but the Gaussian curvature K = κ
max
κ
min
and the mean curvature
H =
1
2
(κ
max
+ κ
min
). The Gaussian and mean curvatures can be computed
without computing the principal curvatures. The principal curvatures are the
roots of the quadratic
det(S − λF)=(EG − F
2
)λ
2
− (EN + GL − 2FM)λ +(LN − M
2
)=0,
and the fact that the sum and product of the roots of a quadratic ax
2
+ bx + c
(with a =0)are−b/a and c/a, yields
K =
LN − M
2
EG − F
2
,H=
1
2
EN + GL − 2FM
EG − F
2
.
The principal, mean, and Gaussian curvatures distinguish the local geome-
try of a surface at a point p as follows.
Elliptic Point: H =0,K > 0. At an elliptic point κ
min
and κ
max
have the
same sign. Therefore the normal sections have the same profile, implying
the surface near p has the shape of an ellipsoid.
Hyperbolic Point: H =0,K < 0. At a hyperbolic point κ
min
and κ
max
have
opposite signs. So the surface near p has the shape of a saddle.
Parabolic Point: H =0,K = 0. So either κ
min
=0orκ
max
= 0. Therefore
the surface is linear in one principal direction, and near p the surface has the
shape of a parabolic cylinder. In computer vision applications the surface
is said to be a ridge or a trough.
Umbilic Point: κ
min
= κ
max
=0(H =0,K > 0). An umbilic point is a
special case of an elliptic point. The normal curvature is constant (non-
zero) and near p the surface has the shape of a sphere.
Flat or Planar Point: κ
min
= κ
max
=0(H = K = 0). The normal curva-
ture is identically zero and the surface near p is flat.
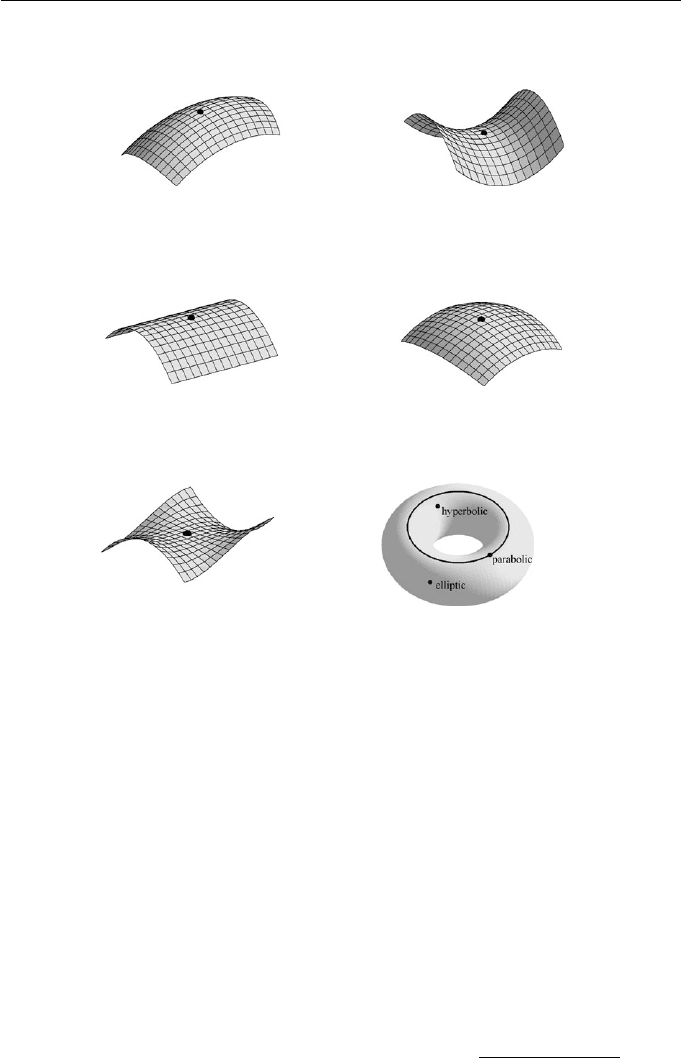
292 Applied Geometry for Computer Graphics and CAD
(a) Elliptic point K>0,H = 0 (b) Hyperbolic point K<0,H =0
(c) Parabolic point K =0,H = 0 (d) Umbilic point κ
max
= κ
min
=0
(e) Planar point κ
max
= κ
min
=0
(f) Elliptic, hyperbolic, and parabolic
points on a torus
Figure 10.7
Example 10.23
Let S(u, v)=(u cos v, u sin v, v), 0 <v<2π, u>0. Then S
u
=(cosv, sin v, 0),
S
v
=(−u sin v, u cos v, 1), and hence E =1,F =0andG =1+u
2
.Fur-
ther S
uu
=(0, 0, 0), S
uv
=(−sin v, cos v, 0), S
vv
=(−u cos v,−u sin v, 0) and
N =
1+u
2
−1/2
(sin v, −cos v, u), and hence L =0,M = −
1+u
2
−1/2
and
N =0.Then
det(S − λF)
=det
0 −
1+u
2
−1/2
−
1+u
2
−1/2
0
− λ
10
01+u
2
=det
−λ −
1+u
2
−1/2
−
1+u
2
−1/2
−λ
1+u
2
=
λ
2
1+u
2
2
− 1
1+u
2
.

10. Curve and Surface Curvatures 293
Solving det(S − λF)=0givesλ =
1+u
2
−1
and λ = −
1+u
2
−1
.The
Gaussian curvature is K = −
1+u
2
−2
, and the mean curvature is H =0.
Since K<0, every point of the surface is hyperbolic.
Example 10.24
Consider the torus S(u, v)=((r cos u + R)cosv, (r cos u + R)sinv, r sin u), for
R>r>0. Then
S
u
(u, v)=(−r sin u cos v, −r sin u sin v, r cos u),
S
v
(u, v)=(−(r cos u + R)sinv, (r cos u + R)cosv,0) ,
S
uu
(u, v)=(−r cos u cos v, −r cos u sin v, −r sin u),
S
uv
(u, v)=(r sin u sin v, −r sin u cos v, 0),
S
vv
(u, v)=(−(r cos u + R)cosv, −(r cos u + R)sinv, 0) .
Thus E = S
u
·S
u
= r
2
, F = S
u
·S
v
=0,G = S
v
·S
v
=(r cos u + R)
2
.Thesur-
face normal is n =(S
u
× S
v
)/ |S
u
× S
v
| =(−cos u cos v,−cos u sin v, −sin u).
Hence L = n · S
uu
= r, M = n · S
uv
=0,N = n · S
vv
=cosu (r cos u + R).
Therefore, LN − M
2
= r cos u (r cos u + R), EG − F
2
= r
2
(r cos u + R)
2
,
K =
r cos u (r cos u + R)
r
2
(r cos u + R)
2
=
cos u
r (r cos u + R)
, and
H =
1
2
r
2
cos u (r cos u + R)+r (r cos u + R)
2
r
2
(r cos u + R)
2
=
r cos u +
1
2
R
r (r cos u + R)
.
Since R>r, the denominator of K is positive. Thus, when 0 ≤ u<π/2
or 3π/2 ≤ u<2π,thencosu>0andK>0. When π/2 <u≤ π or
π/2 ≤ u<3π/2, then cos u<0andK<0. When u = π/2or3π/2, then
K = 0. Thus the torus has regions of elliptic and hyperbolic points separated by
two circles of parabolic points parametrized by S(π/2,v)=(R cos v, R sin v, r),
S(3π/2,v)=(R cos v, R sin v, −r). The partition of the torus according to the
type of point is illustrated in Figure 10.7.
Example 10.25 (Developable Surfaces)
Aircraft wings are constructed from a special honeycomb material which cannot
be shaped by the methods used for plate metal. The wing shape is obtained
by rolling the material. The resulting surface shapes are a special type of ruled
surface known as developable surfaces for which the Gaussian curvature is zero
at every point of the surface. See Exercise 10.31.
294 Applied Geometry for Computer Graphics and CAD
Example 10.26 (Minimal Surfaces)
A surface for which the mean curvature is zero at every point is called a minimal
surface. Minimal surfaces arise in the study of soap films which form on a closed
curve. The surface of a soap film is such that the surface tension is minimized.
The resulting surface is a minimal surface.
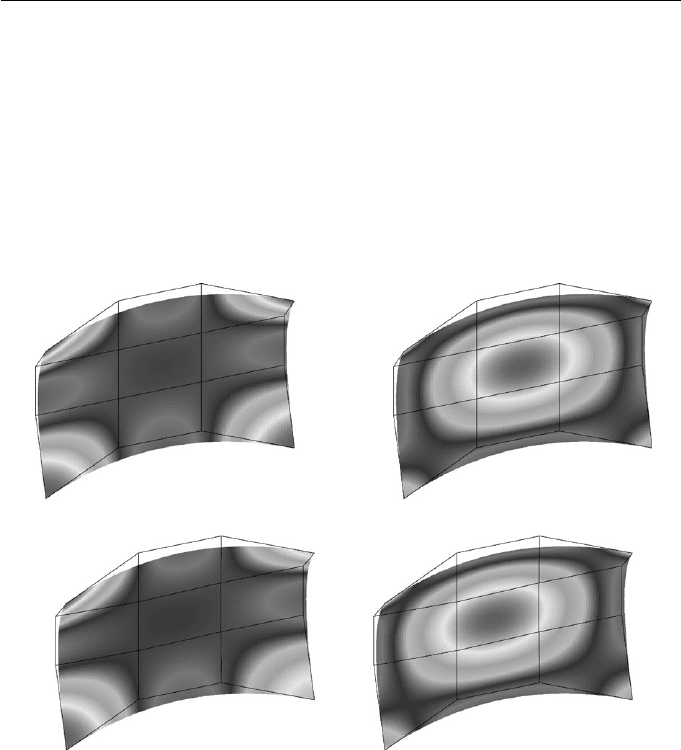
Figure 10.8 Gaussian and mean curvatures for B´ezier surfaces
Example 10.27 (Curvatures of Bezier and B-spline Surfaces)
Curvatures are used to assess the quality of manufactured surfaces. Applica-
tions to the car and ship building industries can be found in [9], [17], [18],
[7]. Surfaces can be coloured to indicate the value of a particular curvature
at a point on the surface. For a B´ezier surface B(s, t), the first and second
order partial derivatives at (s, t)=(0, 0) are easily determined in terms of
the control points using the formulae derived in Section 9.3.2, and the sur-
face curvatures are easily determined from the derivatives. Curvatures at other
parameter values can be obtained by subdivision in a manner similar to com-
puting the curvature of a B´ezier curve. A similar method applies to B-spline

10. Curve and Surface Curvatures 295
surfaces.
To illustrate how curvatures can be used, the plots of two similarly shaped
B´ezier surfaces are shown in Figure 10.8. The darker shades indicate high values
of Gaussian curvature and the lighter shades indicate low values. Note that
although the surfaces look very similar the curvatures show areas of difference.
Such shading techniques (which work better in colour) can be used to highlight
imperfections or potentially troublesome areas such as flat spots (when K =
H =0).
EXERCISES
10.22. Using the notation of Section 10.4, show that a surface S(u, v)is
regular if and only if EG − F
2
=0.
10.23. Consider a curve C(t) on a regular parametric surface S(u, v), and
suppose p = C(t)=S(u, v) is a point on the curve. Let N
p
be the
principal normal of C at p, n
p
be the surface normal at p, κ
p
be the
normal curvature of S in the direction
˙
C, and κ be the curvature
of C at p. Show that if θ is the angle between N
p
and n
p
,then
κ
p
= κ cos θ.
10.24. Determine the principal curvatures of the following surfaces:
(a) S(u, v)=
u, v, u
2
+ v
2
,
(b) S(u, v)=(u, sin v, u +cosv),
(c) Torus: S(u, v)=((R + r cos u)cosv, (R + r cos u)sinv, r sin u).
10.25. Determine the Gaussian and mean curvatures of the following sur-
faces:
(a) Saddle surface: S(u, v)=(u, v, uv),
(b) S(u, v)=
u, v, u
2
− v
2
,
(c) S(u, v)=
u, v, u
3
+ v
3
.
10.26. Determine the umbilics of the following surfaces:
(a) Ellipsoid: S(u, v) = (4 cos u cos v, 2cosu sin v, sin u), 0 ≤ u ≤ 2π,
0 ≤ v ≤ 2π,
(b) S(u, v)=
u, v, u
2
+ v
2
.

296 Applied Geometry for Computer Graphics and CAD
10.27. Show that the following surfaces are minimal (that is, H =0):
(a) Bugle surface: S(u, v)=(a cosh(u/a)cosv, a cosh(u/a)sinv, u),
(b) Scherk’s surface: S(u, v)=(u, v, ln(cos(u)) − ln(cos(v))),
(c) Enneper’s surface:
S(u, v)=
u − u
3
/3+uv
2
,v− v
3
/3+u
2
v, u
2
− v
2
,
(d) Catalan’s surface:
S(u, v)=(u −sin u cosh v, 1 −cos u cosh v, 4 sin(u/2) sinh(v/2)) .
10.28. Show that the parameter curves of Enneper’s surface are lines of
curvature.
10.29. Show that S(u, v)=(u cos v, u sin v, u) is developable (K =0).
10.30. The offset at a distance d of a regular surface S(u, v) with unit
normal N(u, v)isO(u, v)=S(u, v)+d N(u, v) (see Section 9.2.1).
Show that if K and H are the Gaussian and mean curvatures of
S then the offset has Gaussian curvature K/
Kd
2
− 2Hd +1
and
mean curvature (H − Kd)/
Kd
2
− 2Hd +1
.
10.31. Let A(u)andB(u) be unit speed curves. Show that the ruled surface
S(u, v)=A(u)+vB(u) is developable if and only if (A(u) × A
(u))·
B(u) = 0. It can be shown that any developable surface is one of
the following: (i) a cone, i.e A(u) is constant, (ii) a cylinder, i.e.
B(u) is constant, or (iii) a tangential developable, that is, the surface
consisting of all the tangents of a space curve, i.e. B(u)=A
(u).
10.32. The mean value of a function f(t)definedonaninterval[a, b]is
1
b−a
b
a
f(t) dt. By integrating κ
p
(θ)=κ
max
cos
2
θ + κ
min
sin
2
θ over
the interval [0,π], show that the mean value of the normal curvature
κ
p
at a point p is the mean curvature H.
10.33. Write a program or use a package to determine the curvatures of a
B´ezier surface B(s, t) (or B-spline) at a mesh of parameter values
(s
i
,t
j
).
11
Rendering
11.1 Introduction
This chapter introduces techniques for object rendering. The two areas of CAD
and computer graphics have differing opinions of what constitutes a good ren-
dering. In the field of CAD the user needs a highly accurate and well defined
line drawing that conforms to international drawing standards. Further, the
objects must be drawn to scale so that they can be annotated with dimensions.
In contrast, the computer graphics user desires a photographic realism of ob-
jects in a scene showing qualities such as colour, surface texture, and shadow.
The position, shape, direction, and intensity of each light source play an im-
portant role. The following sections consider various elements that contribute
to both accurate CAD drawings and realistic object rendering. Colour is intro-
duced in Section 11.2, and a model for reflected light is developed in Section
11.3. Shading algorithms, which apply the light intensities obtained from the
reflected light model, are discussed in Section 11.4. Section 11.5 introduces a
new geometric feature of a surface, namely, the silhouette. Silhouettes are an
essential feature in CAD drawings, and they are used in Section 11.6 to create
shadow effects.
297
