Marsh D. Applied Geometry for Computer Graphics and CAD

Подождите немного. Документ загружается.

318 Applied Geometry for Computer Graphics and CAD

silhouette can be obtained, for instance, by using (11.24) to solve for s,and

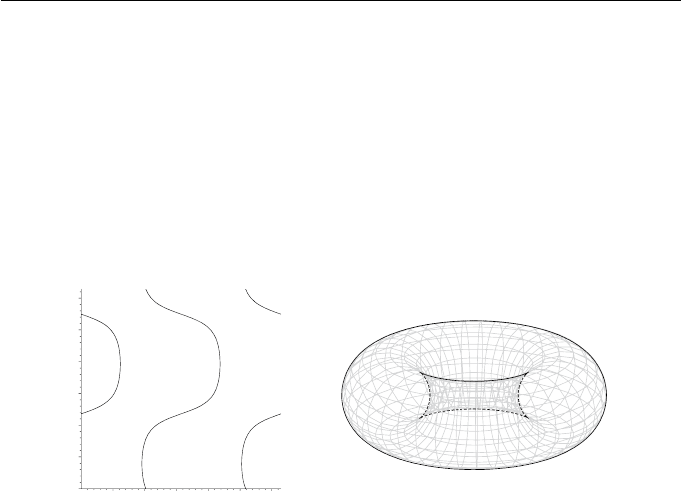
then substituting for s in the parametric equation of the torus. Figures 11.16(a)

and (b) show the curve in the (s, t)-parameter space of the torus, and the

corresponding silhouette when r =5,R =10andV(50, 50, 25). Part of the

silhouette curve is drawn using a dashed line to indicate that that it is hidden by

the torus in the given projection. Observe that the parameter-space curve has

two branches (taking the periodicity of the domain in account). Each branch

corresponds to a connected component of the silhouette curve.

1234

(a) (b)

Figure 11.16 Silhouette of a torus

In general, it is not possible to obtain an analytical solution for the silhou-

ettes of a surface. Silhouettes of more complex surfaces such as B´ezier and B-

spline surfaces are found by numerical methods. One approach is similar to that

used in Example 11.8. For a parametric surface x(s, t)=(x(s, t),y(s, t),z(s, t))

the normal direction is (x

× x

). The silhouette for a parallel projection is

given by the vector triple product

V · (x

× x

)=0. (11.25)

Equation (11.25) deﬁnes a curve C(s, t)=0inthe(s, t) parameter space of

the surface. Points of this curve are obtained numerically using, for instance,

a marching method or subdivision (see [13]). The points of this curve corre-

spond to the silhouette points of the surface. Perspective projections can be

determined similarly.

The CAD drawing in Figure 11.17(a) has been obtained by projecting the

edges and silhouettes of the surfaces. The CAD drawing is completed by per-

forming a hidden line computation to determine the segments of the edges

and silhouettes that are visible. The silhouette plays an important part in the

hidden line calculation. In Figure 11.17(b), the line AC has a visible segment

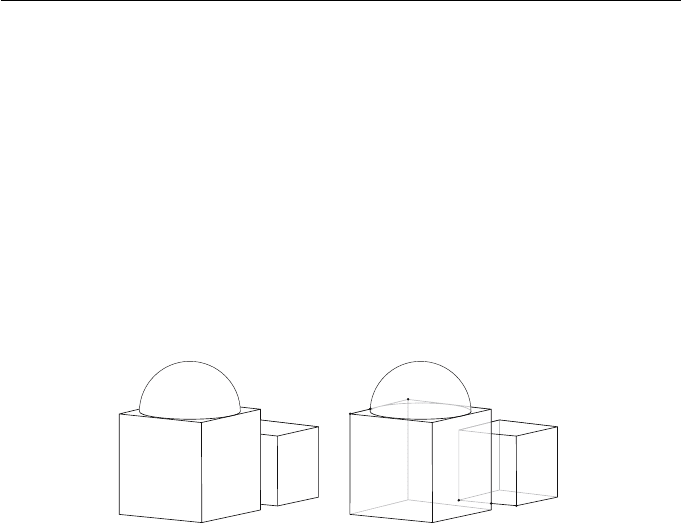
11. Rendering 319

between points A and B, and an invisible segment BC that lies behind the

hemisphere. Similarly, the line DF has a visible segment between points D and

E, and an invisible segment EF that lies behind one of the blocks. Observe

that changes in the visibility of an edge (or a silhouette) correspond to points

in the viewplane where the projected image of the edge (or silhouette) inter-

sects the projected images of itself, and other edges and silhouettes. However,

not all such intersections give rise to a change in visibility, and other infor-

mation about the surfaces must be taken into account. Changes in visibility

can also arise at apparent cusps of a silhouette, that is, silhouette points that

correspond to cusps of the apparent contour. For instance, the visibility of the

torus silhouette in Figure 11.16 changes at two of the four apparent cusps.

(a) (b)

Figure 11.17 CAD drawing with (a) hidden lines removed and (b) hidden

lines drawn faint

EXERCISES

11.12. Show that VQP

= PQV

11.13. Verify that Equations (11.15) and (11.23) are equivalent.

11.14. Compute the silhouette curves of the cylinder x

+ y

= 1 for the

perspective projection with viewpoint (λ, 0, 0), for λ>1orλ<−1.

11.15. Compute the silhouette curve of the quadric 4x

−2xz+y

−z

−4=0

for the perspective projection with viewpoint (10, 0, 0).

11.16. Write a computer program (or use a computer package) that obtains

the silhouettes of a quadric surface. The user should input the co-

eﬃcients of the quadric and the viewpoint, and the program should

determine the conic silhouette in parametric form. Care should be

taken to identify the cases when there are no silhouette points; for

instance, when the viewpoint lies inside a sphere or ellipsoid. The

320 Applied Geometry for Computer Graphics and CAD

cases when the silhouettes are linear may need to be treated sepa-

rately.

11.17. Consider the surface of revolution of the curve (f(u), 0,g(u)) (f(u) =

0) about the z-axis given by x(u, v)=(f(u)cosv,f(u)sinv, g(u)).

Show that the silhouettes for a parallel view in the z-direction are

circles lying in planes that are perpendicular to the z-axis.

11.18. Show that, for a parallel projection in the z-direction, the silhouette

curves of the torus of Example 11.5 are circles.

11.19. Show that, for a parallel projection in the x-direction, the silhouette

curves of the torus of Example 11.5 are circles.

11.6 Shadows

A shadow is a region of a object’s surface where illumination is reduced due to

the obstruction of light sources by other objects in the scene. The amount of

diﬀuse light is reduced, but there is still a contribution of ambient light. When

a shading algorithm is applied to a scene, shadows appear in regions where

the intensities are signiﬁcantly less than the surrounding intensities. Shading

algorithms do not always produce a satisfactory result. For some surfaces it is

possible to determine the boundary of the shadow region mathematically by

applying a projection with the light source as the viewpoint and the surfaces

of objects in the scene as “viewplanes”. The boundaries of an object’s shadow

are the projected images of edges and silhouettes of the obscuring objects onto

the surface.

The shadows cast by a polygonal surface onto a planar surface are straight-

forward to compute. A polygon is a union of triangular planar facets, and it

follows from Exercise 11.4 that each facet either has no silhouette, or is entirely

in silhouette and does not contribute to the shadow. Therefore, a polygon casts

a shadow that is bounded by the projected images of the polygon edges: these

can be found using the method of Section 4.3.

Example 11.9

The scene in Figure 11.18(a) consists of a sphere, with radius

and centre



, 1



, that has been embedded in a unit cube. The shadow cast onto the

plane z = 0 is determined by (i) computing the silhouette of the sphere, (ii)

projecting the silhouette and the edges of the cube using the light source as

viewpoint and the ﬂat surface as viewplane, and (iii) shading the bounded

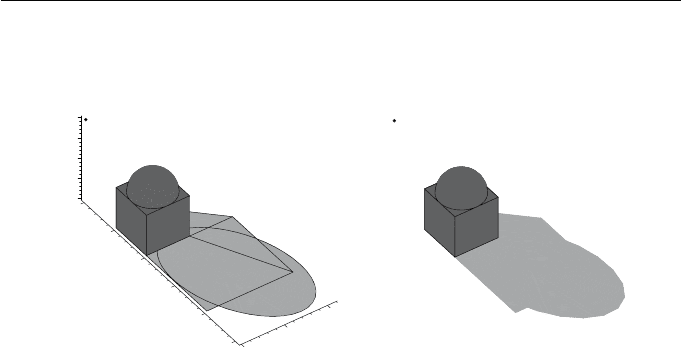
11. Rendering 321

shadow region. The unit cube, viewpoint (−1, 0, 2) and viewplane z =0are

-1

(a) (b)

Figure 11.18

as given in Example 4.18 and so the projection matrix M has already been

determined. The silhouette of the sphere was obtained in Example 11.7. The

projected vertices of the cube are calculated in the usual manner:

⎛

⎜

⎝

0001

1001

1101

0101

0011

1011

1111

0111

⎞

⎟

⎠

⎛

⎜

⎝

−2000

0 −20 0

−1001

000−2

⎞

⎟

⎠

⎛

⎜

⎝

000−2

−200−2

−2 −20−2

0 −20−2

−100−1

−300−1

−3 −20−1

−1 −20−1

⎞

⎟

⎠

giving the points with aﬃne coordinates (0, 0, 0), (1, 0, 0), (1, 1, 0), (0, 1, 0),

(1, 0, 0), (3, 0, 0), (3, 2, 0) and (1, 2, 0). The image of the silhouette can be ob-

tained by either computing points on the circle and applying the projection

matrix, or applying the projection matrix to the equation of the circle to yield

a parametric equation for the silhouette image. The shadow is shown in Fig-

ure 11.18(b).

Solutions

Chapter 1

1.2. −4x − 3y +23=0.

1.4. Use Example 1.2 with θ = π/2, to give A

+ B

=0.

1.6. PQ has parametric equation (x(t),y(t)) = ((1 − t) p

+ tq

, (1 − t) p

+ tq

)

for 0 ≤ t ≤ 1. Then

L (x(t),y(t)) = (ax(t)+by(t)+c, dx(t)+ey(t)+f)

=(a ((1 − t) p

+ tq

)+b ((1 − t) p

+ tq

)+c,

d ((1 − t) p

+ tq

)+e ((1 − t) p

+ tq

)+f)

=(1− t)(ap

+ bp

+ c, dp

+ ep

+ f)

+ t (ap

+ bp

+ c, dp

+ ep

+ f)

=(1− t) L (P)+tL (Q) .

The ﬁnal line deﬁnes the line segment with endpoints L (P)andL (Q).

1.7. (a) A



(4, −1), B



(6, −1), C



(5, 0), D



(4.5, 1). (b) T(−3, 2).

1.8. A mirror image.

1.10. A



(1, −1), B



(3, −1), C



(2, −2), D



(1.5, −3).

1.13. For Rot (π/3) : P



(−0.366, 1.366), Q



(0.634, 3.10), R



(−0.732, 2.732).

For Rot (π/4) : P



(0, 1.414), Q



(1.414, 2.828), R



(0, 2.828).

1.15. No.

1.16. (a) v =(3/5, −4/5) , Sh ((3/5, −4/5) , 4) =



2. 92 −2. 56

1. 44 −0. 92



323

324 Solutions

(b) v =(8/10, 6/10), Sh ((8/10, 6/10) , −1) =



1. 48 0. 36

−0. 64 0. 52



1.17. Bottom left window is obtained from Square by a scaling of 0.5 in the

y-direction followed by a translation of 1.5 units in the x-direction and

1.5 units in the y-direction.

1.20. Apply Exercise 1.6 with t =0.5.

Chapter 2

2.1. (2, 6, 4), (−1, −3, −2), (1, 3, 2), (4, 12, 8).

2.2. (2, −3, 1), (4, −6, 2) etc.

2.3. (−5, 20, 1), (10, −40, 2).

2.4. Reﬂexive: M

∼ M

since M

=1M

. Symmetric: if M

∼ M

then M

µM

for some µ =0.ThenM

and so M

∼ M

. Transitive: if

∼ M

and M

∼ M

,thenM

= µM

and M

= ηM

for some µ =0

and η =0.ThenM

=(µη) M

and µη =0.SoM

∼ M

. Hence ∼ is

an equivalence relation.

2.5. (6, −3, 0).

2.6. (3, 4, 0).

2.7. 3X +4Y − 5W =0.

2.8. (9, 2, 0).

2.9. (−b, a, 0).

2.10. A(1, 1), B(3, 1), C(2, 2), D(1.5, 3).

2.11.

⎛

⎝

200

01.50

001

⎞

⎠

, A



(2, 1.5), B



(6, 1.5), C



(4, 3), D



(3, 4.5).

2.12.

⎛

⎝

010

−100

001

⎞

⎠

, A



(−1, 1), B



(−1, 3), C



(−2, 2), D



(1 − 3, 1.5).

2.13.

⎛

⎝

1/200

02/30

001

⎞

⎠

Solutions 325

2.14.

⎛

⎝

cos θ −sin θ 0

sin θ cos θ 0

001

⎞

⎠

2.16.

⎛

⎝

0 −30

200

001

⎞

⎠

In general, changing the order of transformations results in a diﬀerent

transformation.

2.17.

⎛

⎝

−400

0 −0. 50

001

⎞

⎠

2.18.

⎛

⎝

0 −10

100

−111

⎞

⎠

2.19.

(T (−2, 5) · Rot (−π/3))

−1

= Rot (−π/3)

−1

· T (−2, 5)

−1

= Rot (π/3) · T (2, −5)

⎛

⎝

0. 50. 866 0

−0. 866 0. 50

2.0 −5.01.0

⎞

⎠

2.20.

⎛

⎝

0. 75 0. 3125 0

0. 5 −0. 625 0

−2.0 −2. 51.0

⎞

⎠

2.21. (a) A =

⎛

⎝

cos θ sin θ 0

−sin θ cos θ 0

⎞

⎠

(b) A

−1

⎛

⎝

cos θ −sin θ 0

sin θ cos θ 0

−x

cos θ − y

sin θx

sin θ − y

cos θ 1

⎞

⎠

giving



= x cos θ + y sin θ − y

sin θ − x

cos θ,



= −x sin θ + y cos θ − y

cos θ + x

sin θ.

(d) The equations of the x



-andy



-axes are obtained by setting y



and x



= 0 in the previous equations.

326 Solutions

2.22. T(a, b)wherea = x

cos θ − x

+ y

sin θ − x

cos θ − y

sin θ + x

and

b = −y

− x

sin θ + y

cos θ + x

sin θ − y

cos θ + y

2.23.

⎛

⎝

−21 20 0

20 21 0

−80 32 29

⎞

⎠

2.26. Bottom left window:

⎛

⎝

100

00.50

1. 51. 51

⎞

⎠

2.27.

T (10, 5) · S (20, 20) · T (200, 200) =

⎛

⎝

20 0 0

0200

400 300 1

⎞

⎠

2.28. (1, 3, 1) × (4, −2, 1) = (5, 3, −14), giving 5x +3y − 14 = 0.

2.29. (1, −3, 7) × (4, 3, −5) = (−6, 33, 15), giving (−6/15, 33/15).

Chapter 3

3.1. (1.5, 3, 2.5), (0.5, 1.0, 1.5), (0, 0, 2), (1, 0, 0).

3.2. (3, 4, 1, 0), (7, 2, 0, 0).

3.3. (a)

⎛

⎜

⎝

0. 7071 0. 7071 0 0

−0. 7071 0. 7071 0 0

0010

0001

⎞

⎟

⎠

(b)

⎛

⎜

⎝

1.00 0 0

0 −2. 5981 −1. 50

00. 5 −0. 8660 0

2.02. 5 −4. 3301 1.0

⎞

⎟

⎠

R =(2/3, −2/3, 1/3). Then sin θ

=(−2/3) /



√



= −

√

5, cos θ

(1/3) /



√



√

5, sin θ

=2/3, cos θ

√

5, giving

⎛

⎜

⎝

0. 1111 0. 8889 −0. 4444 0

0. 8889 0. 1111 0. 4444 0

−0. 4444 0. 4444 0. 7778 0

−0. 7407 0. 7407 −0. 3704 1.0

⎞

⎟

⎠

Solutions 327

(d) Then Q − P =(6, 2, 3), and hence R =(6/7, 2/7, 3/7). Then sin θ

(2/7) /



√



√

13, cos θ

=(3/7) /



√



√

13, sin θ

6/7, and cos θ

√

13, giving

⎛

⎜

⎝

0. 5049 0. 6713 0. 5426 0

0. 2427 −0. 7137 0. 6571 0

0. 8283 −0. 2001 −0. 5233 0

−0. 9092 0. 7713 1. 3043 1.0

⎞

⎟

⎠

3.4. (−11, 5, 27).

3.5. 10x +16y + z −25 = 0.

3.8. (a) The points are either collinear or lie on a plane through the origin.

3.9. (p

)=(x

− x

−

−y

), so ω =(x

−y

)=P − Q and v =

−x

)=P×Q. Clearly

−−→

QP = P−Q is the

direction vector of the line.

−−→

OP and

−−→

OQ are vectors parallel to the plane

containing P, Q,andO. The normal to the plane is

−−→

OP ×

−−→

OQ = P ×Q.

3.10. (p

)·(p

)=(x

−x

)·(x

−

−y

)=(x

− y

)(x

− x

)+(x

− y

)(x

− x

− y

)(x

− x

)=0.

3.11. The rotation is Rot

(θ

) Rot

(−θ

) Rot

(θ) Rot

(θ

) Rot

(−θ

), which

after simpliﬁcation using r

+ r

= 1 (following the notation of

Section 3.2.4) yields

⎛

⎜

⎝

(cos θ+

(1 − cos θ)



sin θ+

(1 − cos θ))

(−r

sin θ+

(1 − cos θ))

(−r

sin θ+

(1 − cos θ))

(cos θ+

(1 − cos θ)



sin θ+

(1 − cos θ))

sin θ+

(1 − cos θ))

(−r

sin θ+

(1 − cos θ))

(cos θ+

(1 − cos θ)



0001

⎞

⎟

⎠

3.12. (a) (5 + 6i +11j − 7k), (b) (2, (3, −1, 1)), (c) (8, (44, −22, 48)),

(d) (4, (34, 0, −40)), (e) (4, (8, 24, −46)).

3.13. (a) (1/27, −5/54, 1/18, −2/27), (b) (−3/26, −2/13, 0, 1/26).

328 Solutions

3.14. ijk = −1 implies iijk = −i.Sincei

= −1 it follows that jk = i.Then

jjk = ji and so k = −ji, etc.

3.17. Let q

=(s

, v)fori =1, 2, 3. Then

+ q

)=(s

+ s

) − v

· (v

+ v

)+(s

+ s

+(v

× (v

+ v

)))

=((s

+ v

· v

)+(s

− v

· v

+ s

+(v

× v

)) + (s

+ s

+(v

× v

))

= q

+ q

3.18. (a)

=(s

− v

· v

, −s

− s

− (v

× v

)) and q

−(−v

) ·(−v

), −s

−s

+((−v

) ×(−v

))). The right hand

sides of the two equations are equal so

= q

3.19. I

=(0, v)(0, v) = ((0)(0) − v · v, (0)v +(0)v +(v × v)) = (−|v|

, 0).

3.21. (a) |q| =5,so(2, (1, 2, 4)) = 5





=5(s, v). Lemma 3.11 can

be applied to (s, v): |v| =

√

21/5, and I =

|v|



√



.Let

s =cosθ =2/5(θ =1.1593 radians). Then (2, (1, 2, 4)) = 5(cos θ, sin θI).

3.22. (a)

= r

(cos θ

, sin θ

I) r

(cos θ

, sin θ

= r

(cos θ

cos θ

− (sin θ

I) · (sin θ

I),

cos θ

sin θ

I +cosθ

sin θ

I + ((sin θ

I) × (sin θ

I)))

= r

(cos θ

cos θ

− sin θ

sin θ

, (cos θ

sin θ

+cosθ

sin θ

)I)

= r

(cos(θ

+ θ

), sin(θ

+ θ

)I) .

3.25. I =



−



and q =



cos





, sin







√



−

√



The rotation is given by q(0, (5, 6, 7))q

−1

=(0, (−5/3, 31/3, −2/3)). Thus

(5, 6, 7) rotates to the point (−5/3, 31/3, −2/3).

3.26. Using the fact that

= q

, qq = qq =1,andxx =1,gives

(x)|

= qxq qxq = qxqqx q = qxx q = q q |x|

= |x|

and the result follows.

3.30. φ =1.0745, cos φ =

,andsinφ =

√

341

. The motion is given by

sin(φ(1 − t))

√

341

(6, 0, 18, −9) +

sin(φt)

√

341

(14, 14, 7, 0) .