Marsh D. Applied Geometry for Computer Graphics and CAD

Подождите немного. Документ загружается.

308 Applied Geometry for Computer Graphics and CAD

Consider the triangular facet in Figure 11.9. Let the intensities of the ver-

tices A, B and C,beI

, I

and I

, respectively. Consider a line  (called the

scanline) that moves across the triangle. Suppose  intersects the facet edge

AB in the point L, and the edge AC in the point M. Then, by linear interpo-

lation, L =(1− s)A + sB,forsome0≤ s ≤ 1, and an approximation for the

intensity at L is taken to be

=(1− s)I

+ sI

Similarly, M =(1− t)A + tC,forsome0≤ t ≤ 1, and the intensity of M is

taken to be

=(1− t)I

+ tI

Finally, let P be a point on ,thenP =(1− u)L + uM for some 0 ≤ u ≤ 1,

and an approximate intensity for P is

=(1− u)I

+ uI

. (11.9)

Since the scanline passes over the whole triangle, an intensity for every point

can be computed using Equation (11.9).

The Gouraud shading method described above can be implemented using

the facet normals in the intensity computations as they are less expensive to

compute than true surface normals. However, this results in uneven shading

since pairs of adjacent facets have diﬀerent intensity values along the edge where

the facets meet. Smoother shading can be obtained by averaging the normals of

the facets that contain the vertex, as shown in Figure 11.10. Note that a vertex

may be contained in more than three facets. The average vector is normalized

to obtain a unit vector (so there is no need to divide through by the number of

facets when computing the the average). Since the intensities along an edge are

identical for the two facets containing the edge, the resulting shading is smooth

across the facets. The Gouraud method achieves smoother shading is obtained

at the additional computational cost of averaging and normalizing the facet

normals at each vertex. Figure 11.8(c) shows a rendering of a sphere using the

Gouraud method.

NNNN=+ +

Figure 11.10 Average facet normal

11. Rendering 309

11.4.3 Phong Shading

In Phong shading true surface normals are computed at the facet vertices.

Approximate surface normals at points in the facet are obtained by linearly

interpolating the vertex normals. If the exact surface normals of two vertices

A and B are N

)andN

), then the interpolated normal of

apointL =(1− s)A + sB,for0≤ s ≤ 1, is taken to be the normalization

of N =(1− s)N

+ sN

. The approximate normal of any point in the facet

can be obtained using a scanline method similar to the one used in Gouraud

shading, but normals are interpolated in place of intensities. Since approxi-

mate normals avoid computing surface derivatives, they are more eﬃcient to

use than true surface normals. The Phong method then applies (11.7), using

the approximate normals, to compute the intensities at points in each facet.

The gradual variation of normals across each facet means that Phong shad-

ing produces a smoother and more natural looking shading than both the ﬂat

and Gouraud methods. Figure 11.8(d) shows a rendering of a sphere using the

Gouraud method.

EXERCISES

11.1. Write a computer program that converts a RGB coordinate (r, g, b)

to a HSV coordinate (h, s, v) and vice versa.

11.2. Consider a point light source positioned at (0, 10, 20) shining on

the surface x(s, t)=(s, t, −s

− t

), 0 ≤ s, t ≤ 1. Determine the

reﬂected vector R of the incident ray that hits the surface at the

point x(0.5, 0.5) = (0.5, 0.5, −0.5). Determine the angle of incidence.

11.3. Write a computer program to perform Flat, Gouraud or Phong shad-

ing of an object with polygonal faces.

11.5 Silhouettes

In contrast to the photorealism of computer graphics rendering, CAD drawings

are predominately line drawings with little or no shading. For objects with faces

that are planar, a CAD style drawing can be obtained using projections together

with edge and vertex information. In Section 4.3 it was shown that a parallel

or perspective projection maps a linear edge AB to the linear segment joining

the images of A and B. Projections of non-linear edges can be determined

310 Applied Geometry for Computer Graphics and CAD

by other methods. Sections 7.5.3 and 8.2.1 described techniques for projecting

B´ezier and NURBS curves.

Objects with curved faces cannot be rendered by projecting edges alone.

For instance, a sphere, which has no edges, is rendered by drawing a circle to

represent the extremities of the sphere with respect to the view: the circle is an

example of a silhouette. The ability to compute silhouettes is an essential tool

for CAD drawings.

front

facing

point

back

facing

point

silhouette

point

Figure 11.11

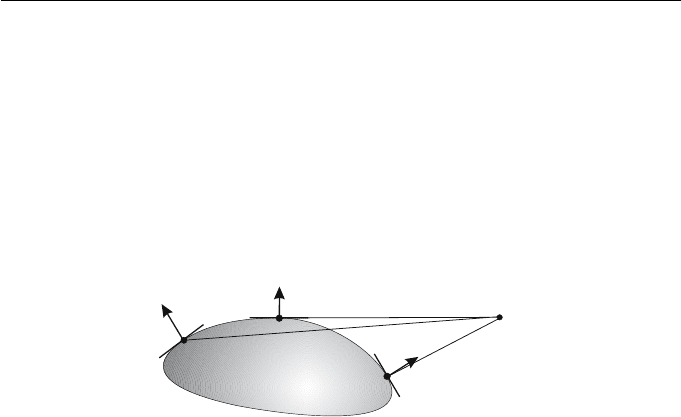
Consider a projection of a surface S from a viewpoint V (considered to

be at inﬁnity for a parallel projection) as shown in Figure 11.11. Let P be a

point on S and let N be the surface normal at P. In a neighbourhood of P the

surface is approximated by the tangent plane which passes through P and has

normal direction N.IfN points towards the viewpoint then a neighbourhood

of P is front-facing and is visible in the given view. Similarly, if N points away

from the viewpoint, then a neighbourhood of P is back-facing and is invisible

in the given view. When N is neither front-facing nor back-facing then, in a

neighbourhood of P, the face is (in general) turning from front-facing to back-

facing and P is called a silhouette point. For a given projection, the set of all

silhouette points of a surface is called the silhouette. The image of the silhouette

in the viewplane is called the apparent contour. Silhouette points are expressed

more precisely in the following deﬁnition.

Deﬁnition 11.1

Let P be a point of a surface S, and let N be a surface normal at P.ThenP is

said to be a silhouette point of a parallel projection in the direction V whenever

V · N =0.P is said to be a silhouette point of a perspective projection from a

viewpoint V whenever (V − P) · N =0.

11. Rendering 311

Example 11.2

Consider the parallel projection of the surface x(s, t)=(s, t, st + s

+ t

)inthe

direction V(0, 1, 0). Then x

(s, t)=(1, 0,t+3s

)andx

(s, t)=(0, 1,s+2t)

and the unit normal is

N =

× x

(−t − 3s

, −s − 2t, 1) .

The silhouette points satisfy V · N = −s − 2t = 0. Therefore s = −2t and

substituting for s in x(s, t) gives the silhouette curve (−2t, t, −t

− 8t

). The

surface and its silhouette are shown in Figure 11.12. Note that the silhouette

calculation does not require the surface normal to be a unit vector, and so the

surface normal will not be normalized in the subsequent examples.

silhouette

curve

Figure 11.12 Surface and silhouette of Example 11.2

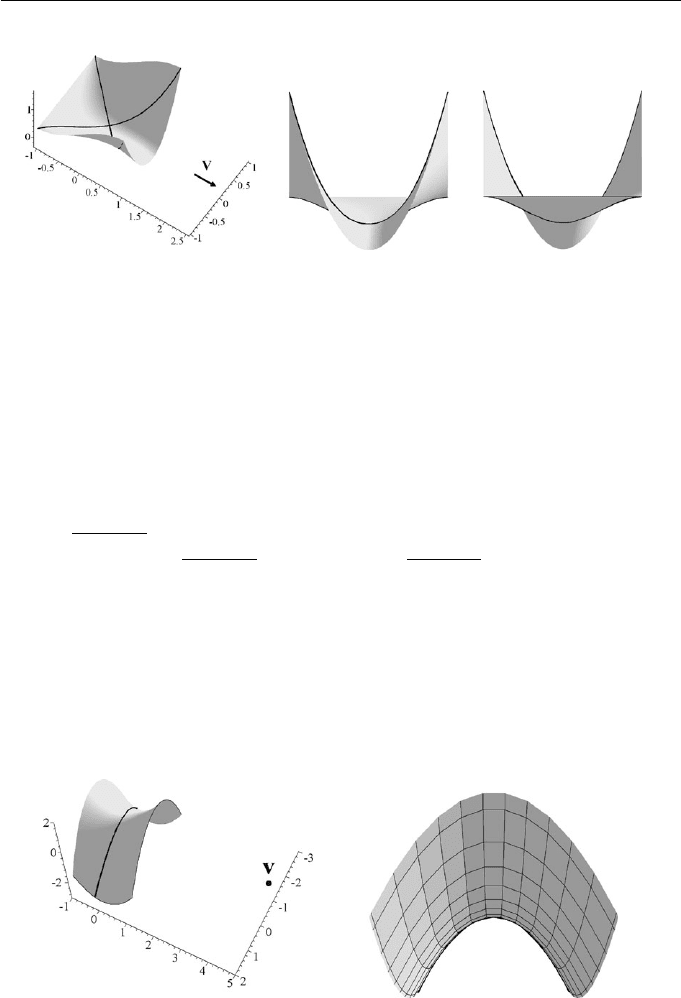
Example 11.3

Consider the parallel projection of the surface x(s, t)=



s, t, st

+ t

−



the direction V(1, 0, 0). Then x

(s, t)=(1, 0,t

−s

)andx

(s, t)=(0, 1, 2st +

2t)andanormalis

N =(s

− t

, −2st − 2t, 1) .

The silhouette points satisfy V · N = s

− t

= 0. Therefore s = t or s = −t.

Substituting s = t in x(s, t) gives the silhouette curve



t, t, t



. Similarly,

substituting s = −t gives a second silhouette curve



−t, t, t

−



. The surface

and the two silhouettes are shown in Figure 11.13(a) and viewed from above.

Figures 11.13(b) and (c) show the surface and silhouettes viewed along the

positive and negative x-axis.

312 Applied Geometry for Computer Graphics and CAD

(a) (b) (c)

Figure 11.13 Surface and silhouettes of Example 11.3

Example 11.4

Consider the perspective projection of the surface x(s, t)=(s, t, t

− s

)from

the viewpoint V(0, 5, 0). Then x

(s, t)=(1, 0, −2s)andx

(s, t)=(0, 1, 2t)and

anormalis

N =(2s, −2t, 1) .

The silhouette points satisfy (V − x(s, t)) · N = −s

+ t

− 10t = 0. Therefore

s = ±



t(t − 10) for t ≤ 0andt ≥ 10. Substituting for s into x(s, t) gives two

silhouette curves (



t(t − 10),t,10t)and(−



t(t − 10),t,10t). An alternative

substitution can be obtained by parametrizing the conic −s

−10t =0using

the method of Section 5.6.4: for instance, (s, t)=



10u/(1 − u

), 10/(1 − u

)



The trigonometric parametrizations of the conic can also be used: (s, t)=

(5 tan θ, 5 sec θ +5) or (s, t)=(5sinhθ, ±5coshθ + 5). The surface and the two

silhouette curves are shown in Figure 11.14(a) and viewed from above. Figure

11.14(b) shows the surface and silhouettes viewed from V(0, 5, 0).

(a) (b)

Figure 11.14 Surface and silhouettes of Example 11.4

11. Rendering 313

Example 11.5 (Silhouettes of a Sphere)

To show that the silhouette of a sphere is a circle, consider the sphere with

radius r and centred at C(x

). In implicit form the sphere is given by

(x − x

)

+(y − y

)

+(z − z

)

= r

(11.10)

and a normal vector at the point P(x, y, z)is

N =(x − x

,y− y

,z− z

)=P − C . (11.11)

The silhouette points of the sphere for a parallel projection with direction

V(v

) satisfy V · N = 0 giving

(x − x

)+v

(y − y

)+v

(z − z

)=0. (11.12)

Equation (11.12) deﬁnes the plane through C with normal direction V.There-

fore, the silhouette curve is the intersection of the sphere with the plane (11.12),

that is, a circle centred at C with radius r.

For a perspective projection with viewpoint V(v

), the silhouette

points of the sphere (11.10) satisfy (V − P) · N = 0 and hence

(V − P) · (P − C)=0. (11.13)

In vector form, the sphere (11.10) is given by

(P − C) · (P − C)=r

. (11.14)

Adding Equations (11.13) and (11.14) gives

(V − C) · (P − C)=r

which, after some rearrangement of the equation, gives

(V − C) · P = r

+ C · (V − C) . (11.15)

Therefore, the silhouette points lie on a plane with normal direction V − C.

Intersecting the plane (11.15) with the sphere (11.10) gives a silhouette circle.

See Exercise 11.7 for further details.

314 Applied Geometry for Computer Graphics and CAD

EXERCISES

11.4. Determine the silhouette curve of the surface x(s, t)=(s, t, st + s

−

) for a parallel projection in the direction V(0, 1, 0).

11.5. Determine the silhouette curve of the surface x(s, t)=(s, t, st

−

s +

) for a parallel projection in the direction V(1, 0, 0). (Hint:

the substitution s =cosθ and t =sinθ might be helpful for the

parametrization of the silhouette curve.)

11.6. Determine the silhouette curve of the surface x(s, t)=(s, t, 9s

t −

t − 3t

) for a parallel projection in the direction V(0, 1, 0).

11.7. Show that, for a parallel or perspective projection, a plane either

has no silhouette points or the entire plane is “in silhouette” (that

is, every point of the plane is a silhouette point).

11.8. Generalise the method shown for a sphere to determine the silhouette

plane of the ellipsoid

= 1 for a parallel projection in

the direction V(v

11.9. Show that, for a given projection, the silhouette of a surface is the

locus of points on the surface for which there is a tangent line passing

through the viewpoint (considered to be at inﬁnity for a parallel

projection).

11.10. Consider the perspective projection of the sphere of Example 11.6.

a) Show that the distance from the silhouette plane (11.12) to the

sphere centre C is d = r

/ |V − C|.

b) Let U =(V − C)/ |V − C| denote the silhouette plane unit

normal. Show that the silhouette circle has centre C

and radius

given by

= C + dU, and r

=(r

− d

)

1/2

c) Let X be a unit vector perpendicular to U, and let Y =

(U × X) /|U×X|. Using C

as the origin, and X and Y as the x-

and y- axes for the silhouette plane, write down a parametriza-

tion for the silhouette circle.

11.11. Show that, for a perspective projection, the sphere (11.10) has no

silhouette points when the viewpoint is inside the sphere.

Silhouette curves of quadric surfaces are relatively straightforward to com-

pute since they can be shown to lie in a silhouette plane. The intersection of

11. Rendering 315

the silhouette plane with the quadric yields silhouette curves that are conics.

Consider a quadric with the homogeneous equation

xQx

=0, (11.16)

and a projection with viewpoint V (using homogeneous coordinates). The aim

is to apply Exercise 11.6 to obtain the silhouette. Let P be a point on the

quadric so that PQP

= 0. The line through P and V is

x(s)=(1− s)P + sV . (11.17)

It follows that the point x(s) lies on the quadric whenever

x(s)Qx(s)

= ((1 − s)P + sV)Q((1 − s)P

+ sV

)=0. (11.18)

Expanding (11.18), gives a quadratic equation in s

(1 − s)

PQP

+ s(1 − s)VQP

+ s(1 − s)PQV

+ s

VQV

=0. (11.19)

Since PQP

=0andVQP

= PQV

(Exercise 11.12), it follows that Equa-

tion (11.19) simpliﬁes to

2s(1 − s)VQP

+ s

VQV

=0. (11.20)

Applying Exercise 11.9, P is a silhouette point if and only if the line (11.17)

is tangent to the quadric at P, which can occur if and only if (11.20) has a

multiple root. Since s = 0 is a root, a multiple root can can only arise when

VQP

=0. (11.21)

This is the condition for P to be a silhouette point of the quadric (11.16).

Example 11.6

Consider a projection of the sphere (x−x

)

+(y −y

)

+(z −z

)

−r

=0from

a viewpoint V(v

). Condition (11.21) implies that P(X, Y, Z, W)isa

silhouette point whenever





⎛

⎜

⎝

100 −x

010 −y

001 −z

−x

−y

−z

+ y

+ z

− r

⎞

⎟

⎠

⎛

⎜

⎝

⎞

⎟

⎠

=0,

yielding the silhouette plane,

− v

)X +(v

− v

)Y +(v

− v

−(v

+ v

+ y

+ z

− r

))W =0. (11.22)

316 Applied Geometry for Computer Graphics and CAD

For a parallel projection, v

= 0, and in aﬃne coordinates (11.22) gives

x + v

y + v

z − (v

+ v

)=0.

This agrees with Equation (11.12). For a perspective projection, set v

=1,so

that in aﬃne coordinates (11.22) yields

−x

)x+(v

−y

)y+(v

−z

)z−(v

+(x

−r

)) = 0 .

(11.23)

It left as an exercise to the reader (Exercise 11.13) to verify that this equation

is equivalent to (11.15) .

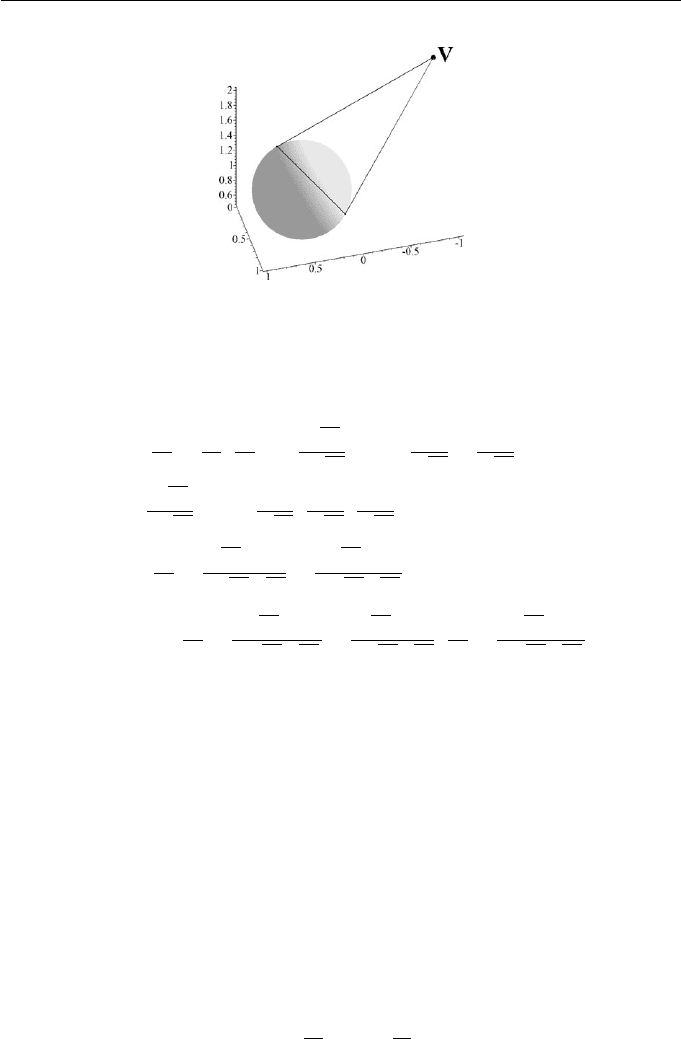
Example 11.7

Consider the sphere



x −





y −



+(z − 1)

with radius

and

centred at



, 1



. For a perspective projection with viewpoint (−1, 0, 2),

Equation (11.23) can be applied to yield the silhouette plane

−

x −

y + z −

=0.

The silhouette curve is the circle of intersection of the silhouette plane and the

sphere. Using Exercise 11.7(a) and (b),

|V − C| =





−

, −

, 1





√

, and d =

√

It follows that the circle has radius r

√

and centre

C =



, 1





−

, −

, 1





−

, −



A parametric equation for the silhouette circle can be obtained using Exercise

11.7(c). The silhouette plane has unit normal U =

√

(−3, −1, 2). The x-axis

for the silhouette plane is chosen to be X =(1/

√

10, −3/

√

10, 0), a unit vector

perpendicular to U.They-axis is Y =(3/

√

35, 1/

√

35, 5/

√

35), the unit vector

with direction U × X. In this coordinate system, the silhouette circle has the

11. Rendering 317

Figure 11.15 Silhouette of Example 11.7

parametric equation

C + r

cos θX + r

sin θY



−

, −



√

cos θ



√

, −

√

, 0



√

sin θ



√





−

√

13 cos θ

√

13 sin θ

√

−

√

13 cos θ

√

13 sin θ

√

13 sin θ

√



The sphere and the circular silhouette are shown in Figure 11.15.

Example 11.8

Consider the torus x(s, t)=((r cos s + R)cost, (r cos s + R)sint, r sin s)for

0 ≤ s ≤ 2π and 0 ≤ t ≤ 2π. The unit normal of the torus is

N(s, t)=(−cos s cos t, −cos s sin t, −sin s) .

The silhouette for a parallel projection in the direction V(v

) satisﬁes

V · N = 0 giving

(cos s cos t)+v

(cos s sin t)+v

sin s =0,

and therefore

tan s = −

cos t −

sin t. (11.24)

Equation (11.24) deﬁnes the curve in the (s, t)-parameter space of the torus

that corresponds to the silhouette of the torus. A parametric equation for the