Marsh D. Applied Geometry for Computer Graphics and CAD

Подождите немного. Документ загружается.

258 Applied Geometry for Computer Graphics and CAD

The derivation of the Gordon–Coons surface can be generalised to give a

loft surface that interpolates four boundary curves c(t), d(t), e(s)andf (s)and

satisﬁes four derivative conditions c

(t), d

(t), e

(s)andf

(s). The surface is

given by

x(s, t)=H(s)

⎛

⎜

⎝

−x

0,0

−x

0,1

−e

(0) −f

(0) c(t)

−x

1,0

−x

1,1

−e

(1) −f

(1) d(t)

−c

(0) −c

(1) −x

st,0,0

−x

st,0,1

(t)

−d

(0) −d

(1) −x

st,1,0

−x

st,1,1

(t)

e(s) f(s) e

(s) f

(s) 0

⎞

⎟

⎠

H(t)

, (9.23)

where

H =





and

0,0

= c(0) = e(0) , x

0,1

= c(1) = f(0) ,

1,0

= d(0) = e(1) , x

1,1

= d(1) = f(1) .

Note that the left hand H of Equation (9.23) is a function of s and the right

hand H

is a function of t. All the entries in the matrix can be obtained from

the speciﬁed curve and derivative data except for those involving x

. The four

values x

st,0,0

, x

st,0,1

, x

st,1,0

and x

st,1,1

are called twist vectors, and specify the

second order partial derivatives

∂

∂s∂t

(s, t) at the corners of the surface. They

can be used to control the shape of the interior of the surface without changing

the shape of the boundary curves.

The loft surface (9.23) can be used to obtain a G

network surface deﬁned

by a grid of curves in a similar manner to the skin surface. In the case of a

network surface, the second order derivative terms x

st,i,j

must satisfy additional

compatibility conditions in order to achieve continuity at the corners:

st,0,0

(0) =

(0) , x

st,0,1

(0) =

(1) ,

st,1,0

(1) =

(0) , x

st,1,1

(1) =

(1) .

Example 9.27

Consider a Gordon–Coons surface given by linear boundary curves in the z =0

plane: c(t)=(0,t,0), d(t)=(1,t,0), e(s)=(s, 0, 0), and f (s)=(s, 1, 0). Let

the derivative conditions be c

(t)=(1, 0, 0), d

(t)=(1, 0, 0), e

(s)=(0, 1, 0),

9. Surfaces 259

and f

(s)=(0, 1, 0). Then

x(s, t)=H(s)

⎛

⎜

⎝

−(0, 0, 0) −(0, 1, 0) −(1, 0, 0) −(1, 0, 0) (0,t,0)

−(1, 0, 0) −(1, 1, 0) −(1, 0, 0) −(1, 0, 0) (1,t,0)

−(1, 0, 0) −(0, 1, 0) −x

st,0,0

−x

st,0,1

(0, 1, 0)

−(1, 0, 0) −(0, 1, 0) −x

st,1,0

−x

st,1,1

(0, 1, 0)

(s, 0, 0) (s, 1, 0) (1, 0, 0) (1, 0, 0) (0, 0, 0)

⎞

⎟

⎠

H(t)

If the twist vectors have zero z-component, then the Gordon–Coons surface has

zero z-component and so the surface is planar. However, if the twist vectors are

chosen so that they point out of the z = 0 plane, then the surface is no longer

planar despite the fact that the boundary curves and the derivatives lie in the

plane. The twist vectors provide a potentially powerful tool for surface design.

EXERCISES

9.19. Determine a skin surface that interpolates the curves c(t)=(3t

4, 2t

, −t)andd(t)=(2t, −t

, 2t +4),for0≤ t ≤ 1.

9.20. Let c(t)=(3t

, 2t

,t)andd(t)=(2t +10, 3t, 2t

). Determine the

loft surfaces that interpolate c(t)andd(t), and satisfy the derivative

conditions

a) c

(t)=(1, 1, 0) and d

(t)=(0, −1, 0),

b) c

(t)=(0, −t

, 0) and d

(t)=(−1,t

, −1).

9.21. Determine the Coons surface interpolating the four boundary B´ezier

curves

c(t)=(−5, −5, 0)B

0,1

(t)+(20, 3, 0)B

1,1

(t),

d(t)=(−8, 0, 10)B

0,2

(t)+(10, 16, 4)B

1,2

(t)+(27, 7, 10)B

2,2

(t),

e(s)=(−5, −5, 0)B

0,3

(s)+(−6, −4, 3)B

1,3

(s)

+(−7, −2, 7)B

2,3

(s)+(−8, 0, 10)B

3,3

(s),

f(s)=(20, 3, 0)B

0,2

(s)+(22, 5, 4)B

1,2

(s)+(27, 7, 10)B

2,2

(s).

9.22. Show that if two surfaces meet at a point P and the surfaces have

a common normal direction at P, then the surfaces meet with G

continuity.

9.23. Consider the skinning operation through two section curves with

general blending functions functions f

(s)andf

(s) that satisfy

260 Applied Geometry for Computer Graphics and CAD

(0) = f

(1) = 1, f

(1) = f

(0) = 0 and f

(s)+f

(s) = 1. Show

that the skin surface

x(s, t)=f

(s)c(t)+f

(s)d(t)

is planar whenever the boundary curves are coplanar.

9.24. Verify that the partial derivatives of the loft surface x(s, t)givenby

(9.18), and evaluated at s =0ands = 1, agree with the speciﬁed

derivative conditions c

(t)andd

(t) respectively.

9.25. Suppose two B´ezier surfaces B(s, t)=



i=0



j=0

i,j

i,n

(s)B

j,p

(t)

and C(s, t)=



i=0



j=0

i,j

i,n

(s)B

j,p

(t) (for (s, t) ∈ [0, 1]×[0, 1])

meet along a common boundary B(1,t)=C(0,t). Determine condi-

tions on the control points for the surfaces to have the same tangent

planes along the boundary.

9.7 Geometric Modelling and CAD

Geometric modelling is concerned with developing tools to create, represent,

and manipulate geometric shapes. Every commercial CAD system incorporates

a geometric modeller, an implementation of modelling tools that enable the user

to specify curves, surfaces and solids. Most systems are able to represent the

curve and surface types that were introduced in the earlier chapters such as

lines, conics, planes, quadrics, and B´ezier and B-spline curves and surfaces.

Geometric modellers make a careful distinction between surfaces and solids.

The term “sphere”, for instance, can refer to either the outer boundary surface

or to the solid consisting of the boundary and all the points inside. A solid

is a ﬁnite volume bounded by a ﬁnite number of surfaces. The intersections

of the bounding surfaces give the edges of the solid, and the intersections of

the edges give the vertices. For example, a solid cube is bounded by six planes.

The planes intersect to give twelve linear edges, and the edges intersect in eight

vertices. Each face of a cube is a planar region bounded by four of the edges.

In addition to the mathematical deﬁnitions of the surfaces and edges, a

speciﬁcation of a solid requires information about the topology of the model,

that is, how the surfaces, edges and vertices interconnect. Not all modellers

can represent solids, and so those that do are referred to as solid modellers.A

number of diﬀerent representations are used in both industrial and academic

modellers and some of these are described in the following sections.

9. Surfaces 261

9.7.1 Wireframe Modeller

A wireframe modeller uses curves to represent both surfaces and solids. Typi-

cally, the curves comprise the boundaries of each surface, and additional (pa-

rameter) curves to indicate the shape of each surface. The surfaces and solids

are not fully represented and no topological information is stored. Wireframe

modellers are very easy to implement and are useful for obtaining fast render-

ings of surfaces.

9.7.2 Surface Modeller

A surface modeller represents each surface mathematically, but no topological

information is stored and, therefore, there is no true concept of a solid. The

simplest type of surface modeller is the polyhedral modeller for which the sur-

faces are all planar. More sophisticated surface modellers are able to represent

B´ezier, B-spline and NURBS surfaces, and general parametric surfaces. Surface

modellers are useful for product concept, speciﬁcation and styling, and may be

suﬃcient for some applications such as numerical controlled (NC) machining

and computer-aided manufacture (CAM).

9.7.3 Constructive Solid Geometry (CSG) Modellers

A constructive solid geometry (CSG) modeller uses implicit surface deﬁnitions

(see Section 9.1). An implicitly deﬁned surface f(x, y, z) = 0 partitions the

three-dimensional workspace into two regions or half-spaces consisting of points

satisfying f(x, y, z) ≥ 0andf(x, y, z) ≤ 0 respectively. (Half-spaces can also

be constructed using > and <.) For instance, the unit sphere with the implicit

equation x

+ y

+ z

− 1 = 0 yields two half-spaces: the inside of the sphere,

which is the set of points (x, y, z) satisfying x

−1 ≤ 0, and the outside

which is the set of points satisfying x

+ y

+ z

− 1 > 0. Likewise, an inﬁnite

plane divides the workspace into the two regions on either side of the plane.

Solids are deﬁned in terms of half-spaces. For example, a hemisphere comprises

the points satisfying both x

+ y

+ z

− 1 ≤ 0andz ≥ 0, that is, the set of

points inside the sphere and to one side of the plane z =0.

The constructive solid geometry (CSG) modeller pre-deﬁnes a number of

solids called primitives. Common primitives include solids derived from planar

and quadric geometries such as spheres, cubes, cylinders and cones. A solid

can be represented by the modeller if it is one of the primitives or can be

constructed from the primitives by applying one or more modelling operations,

262 Applied Geometry for Computer Graphics and CAD

such as linear transformations (see Chapters 1 and 2), and Boolean operations.

Three Boolean operations are used: union, intersection and diﬀerence. Let

A and B be two sets of points representing solids or half-spaces. Then the

union of A and B, denoted A ∪ B, is the set of all points contained in A or B

(including those points in both A and B). The intersection of A and B, denoted

A ∩ B, is the set of all points contained in both A and B.Thediﬀerence of A

and B, denoted A \B, is the set of all points contained in A but not contained

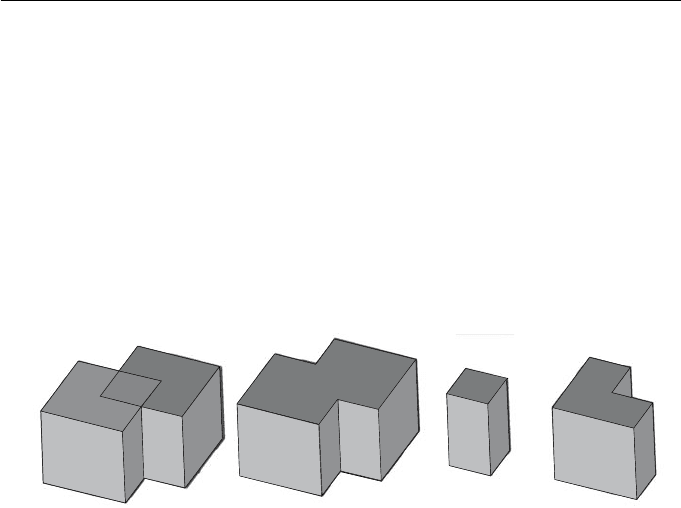
in B. Figure 9.18 exempliﬁes the three operations for two solid blocks. Boolean

operations are a more general concept than presented here and can be deﬁned

for sets of any objects.

(a) (b) (c) (d)

Figure 9.18 (a) Blocks A and B, (b) union A ∪B, (c) intersection A ∩B,

and (d) diﬀerence A \ B

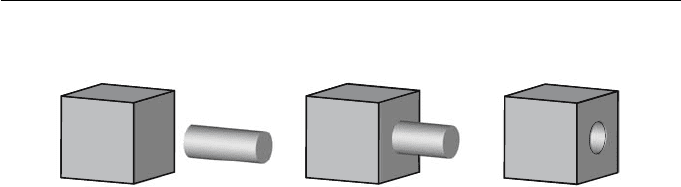
Example 9.28 (Boolean Operations)

In order to cut a hole in a block of material A (called the blank) it is necessary

to construct an object (called the tool ) that has the shape of the required hole.

Let B be a cylindrical tool. A transformation is applied to B so that it overlaps

the region of A where the hole is to be cut. Note that the tool can be larger

than the required hole. The material that is to be removed from the block is

obtained by performing the diﬀerence operation A \B as shown in Figure 9.19.

Whenever modelling operations are applied to objects there is a potential

problem that the result is invalid, that is, it cannot be represented by the mod-

eller. For instance, a modeller that can only represent curves and surfaces in

B´ezier form cannot represent the intersection of two B´ezier surfaces since the

curve of intersection is not (in general) a B´ezier curve. One of the strengths of

the CSG representation is that Boolean operations are guaranteed to give valid

results. Further, the implicit surface deﬁnitions make it straightforward to per-

9. Surfaces 263

(a) (b) (c)

Figure 9.19 Cutting a hole using a Boolean operation

form interrogations such as determining whether a point lies inside or outside

of a solid or on a boundary surface. However, the implicit representations and

the lack of topological information makes rendering computationally expensive

since the edge and boundary information needs to be computed before it can

be drawn.

9.7.4 Boundary Representations (B-rep)

B-rep modellers distinguish the topology of a model from its geometry. A solid

has three main topological entities, namely, faces, edges and vertices corre-

sponding to the geometric entities surfaces, curves and points. The geometric

entities store information about shape such as the coordinates of a point, the

deﬁning function of a parametric curve or surface, or the control points and

knots of a B-spline curve or surface. The topological entities store information

about their relationship to the other entities together with a reference to the

corresponding geometric entity. B-rep modellers commonly use the following

terminology.

Vertex : A vertex represents a point that speciﬁes where edges meet.

Edge: An edge represents a ﬁnite arc of a curve bounded by two vertices, and

speciﬁes where two faces intersect.

Loop : A loop is a connected sequence of edges.

Face : A face represents a ﬁnite region of a surface bounded by one outer loop

and a number of inner loops. The inner loops cannot be nested and must

not intersect.

Shell: A shell is a collection of connected faces.

Solid: A solid is a union of volumes enclosed by shells.

B-rep modellers may also represent non-solid objects such as a sheet which

is deﬁned by a face and does not necessarily bound a ﬁnite volume, and a wire

264 Applied Geometry for Computer Graphics and CAD

which is deﬁned by a connected sequence of edges.

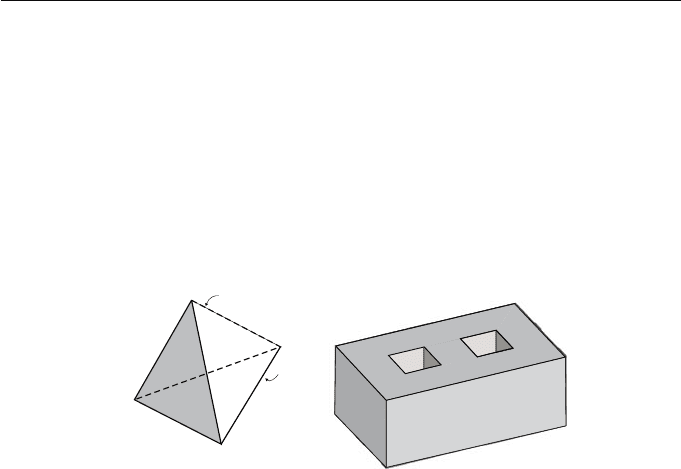
Example 9.29

Consider the tetrahedron of Figure 9.20(a). There are four vertices V

, V

, six edges E

, E

, and four faces F

, F

.Face

has one loop of edges E

→ E

. Edge E

has vertices V

and

(a) (b)

Figure 9.20

Example 9.30

Consider Figure 9.20(b) showing a block with two holes. The solid is deﬁned

by one shell with 14 faces. Twelve of the faces are rectangular and each has

one loop of four edges and four vertices. The two remaining faces, forming the

top and bottom of the object, have three loops each: one outer and two inner.

The solid is deﬁned by 24 vertices, 36 edges, 14 faces and one shell.

The separation of the topology and the geometry is an important aspect

of the B-rep. The topology of two instances of a tetrahedron, for example,

is identical, whereas the underlying geometry, such as the coordinates of the

vertices, may diﬀer. An application of a non-singular transform to a solid has

no eﬀect on the topology, but it does change the geometry.

Solids with more than one shell arise, for instance, when the solid contains

a void. Voids are obtained by the Boolean subtraction A \ B of two solids

whenever B is contained in the interior of A. Multiple shells also arise when a

Boolean operation causes a volume to be cut into disjoint volumes called lumps.

In CAD applications a solid object is said to be manifold whenever the

following conditions are satisﬁed:

9. Surfaces 265

1. All edges and faces are bounded.

2. Edges only intersect at vertices.

3. Faces only intersect in edges.

4. Edges are contained in exactly two faces.

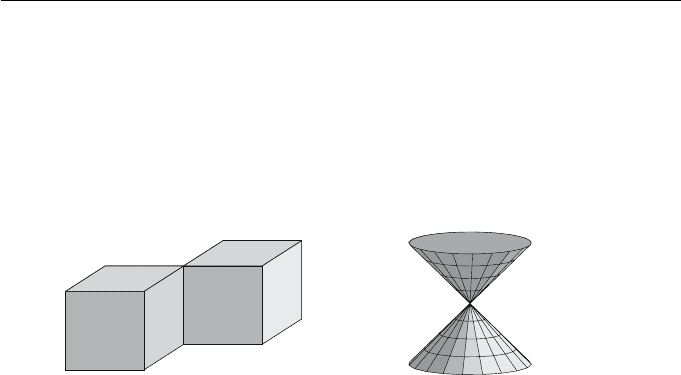
(a) (b)

Figure 9.21 Non-manifold bodies

Figure 9.21 shows examples of non-manifold objects. In the process of ap-

plying Boolean operations to manifold objects it is possible to obtain objects

that are no longer manifold. For instance the object of Figure 9.21(a), which

violates condition (4) above, can be obtained by applying the union operation

to two blocks. The solid of Figure 9.21(b) violates condition (3).

As a sanity check, solids must satisfy the Euler–Poincar´eFormula

V − E + F − I =2(S − H) (9.24)

where V , E, F , I, S,andH are the numbers of vertices, edges, faces, inner

loops, shells, and holes, respectively. The solid of Example 9.30 satisﬁes the

Euler–Poincar´e formula since there are 24 vertices, 36 edges, 14 faces, and two

holes. Further, there are two faces, each with two inner loops, giving 4 loops in

total, and therefore yielding the identity 24 − 36 + 14 − 4=2(1− 2).

A B-rep modeller is considered to be more versatile than a CSG modeller

because it is possible to deﬁne objects with complex boundary faces using

B-splines or general parametric surfaces, whereas a CSG modeller is limited

to solids obtained from the primitives. The operation of determining whether

a point lies inside or outside of a solid, or on a boundary surface is often

computationally expensive for a B-rep modeller than for a CSG modeller which

can yield the information from the half-spaces deﬁning the solid.

CSG modellers retain information about the Boolean operations used to

construct a solid. So if a user wishes to make a change to a model parameter

such as the position of a vertex or the radius of a sphere, then the solid can

easily be reconstructed by repeating the Boolean operations on the objects with

266 Applied Geometry for Computer Graphics and CAD

the new dimensions. To emulate the CSG data structure, some B-rep modellers

have a model design history that retains information about how each solid is

created so that the system can repeat the design process if a user modiﬁes a

parameter, or wishes to “undo” an operation to rectify an error. The danger

for a B-rep system is that some modiﬁcations can result in self-intersections or

other types of invalid model. In view of the pros and cons, the reader should

not be surprised to learn that all the leading commercial CAD modellers use

the B-rep method or a hybrid of B-rep and CSG representations.

EXERCISES

9.26. The B-rep data structure is complex and a number of similar so-

lutions have been proposed. Investigate Baumgart’s winged-edge B-

rep structure and two improved representations: M¨antyl¨a’s half-edge

structure [16] and Braid et al. [4].

9.27. Euler operations are a set of primitive operations that can be applied

to a solid to give a new solid that satisﬁes the Euler–Poincar´eformula

(9.24) and therefore maintains validity. Investigate. See Toriya [16].

Curve and Surface Curvatures

The aim of this chapter is to discuss the local geometry of a curve or surface.

In particular, to determine measures of how much a curve or surface “bends”,

and to describe the shape of a curve or surface in the vicinity of a point on

that curve or surface. These measures or “curvatures” have applications in

determining the quality, or isolating imperfections of, the curves and surfaces

produced by a designer using a CAD package.

10.1 Curvature of a Plane Curve

Let C(t)=(x(t),y(t)) be a regular parametric plane curve deﬁned on an in-

terval I (open or closed). It is assumed that C(t)isC

-continuous (that is,

the derivatives of x(t)andy(t) exist and are continuous) and that higher order

derivatives exist whenever the context suggests that they are required. In Sec-

tion 5.4 it was shown that a regular curve can be reparametrized with respect

to the arclength parameter s to give a unit speed curve. The curve C(t) and its

unit speed reparametrization C(t(s)) are both denoted by C. Diﬀerentiation

with respect to a general parameter will be denoted by a “ · ” and diﬀerentia-

tion with respect to the unit speed parameter will be denoted by a “



”. For

instance,

C =

and C



. Recall that

s(t)=





(˙x(u))

+(˙y(u))



1/2

267