Marsh D. Applied Geometry for Computer Graphics and CAD
Подождите немного. Документ загружается.

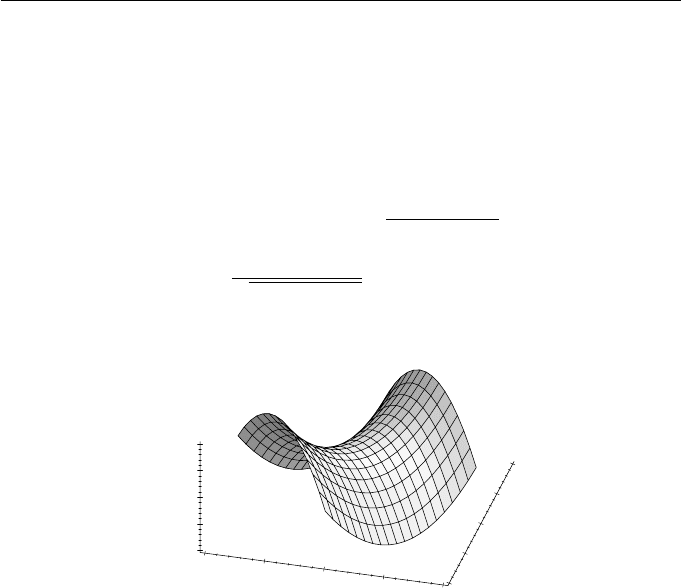
228 Applied Geometry for Computer Graphics and CAD
Example 9.5
The saddle surface S(s, t)=(s−t, s+t, s
2
−t
2
), for (s, t) ∈ R
2
, is the parametric
surface illustrated in Figure 9.2. The curves drawn on the surface are a number
of its parameter curves. Then, S
s
(s, t)=(1, 1, 2s), S
t
(s, t)=(−1, 1, −2t), and
S
s
(s, t) × S
t
(s, t)=(1, 1, 2s) × (−1, 1, −2t)=(−2(s + t), −2(s − t), 2) ,
|S
s
(s, t) × S
t
(s, t)| =2
1+2t
2
+2s
2
,
N(s, t)=
1
√
1+2t
2
+2s
2
(−s − t, −s + t, 1) .
The saddle surface can also be expressed in the implicit form xy − z =0.
-2
-1
0
1
2
x
-2
-1
0
1
2
y
-1
-0.5
0
0.5
1
z
Figure 9.2 Saddle surface (s − t, s + t, s
2
− t
2
)
9.2 Quadric Surfaces
A quadric is an implicit surface defined by a quadratic polynomial
Q(x, y, z)=ax
2
+2bxy +2cxz + dy
2
+2eyz + fz
2
+2gx +2hy +2jz + k =0, (9.2)
for constants a, b, c, d, e, f, g, h, j,andk. All planar sections of a quadric are
conics. Let p =(x, y, z, 1). The quadric surface (9.2) may be represented in the
matrix form Q(x, y, z)=pQp
T
=0,
Q(x, y, z)=
xyz1
⎛
⎜
⎜
⎝
abcg
bdeh
cefj
ghjk
⎞
⎟
⎟
⎠
⎛
⎜
⎜
⎝
x
y
z
1
⎞
⎟
⎟
⎠
=0.

9. Surfaces 229
Apoint(x, y, z) of the quadric is singular if and only if Q(x, y, z)=0and
∂Q
∂x
(x, y, z)=ax + by + cz + g =0, (9.3)
∂Q
∂y
(x, y, z)=bx + dy + ez + h =0, (9.4)
∂Q
∂z
(x, y, z)=cx + ey + fz + j =0. (9.5)
Equation (9.2) can be expressed in the form
Q(x, y, z)=(ax + by + cz + g) x +(bx + dy + ez + h) y
+(cx + ey + fz + j) z +(gx + hy + jz + k)=0,
and it follows from (9.3)–(9.5) that a singular point also satisfies
gx + hy + jz + k =0. (9.6)
Thus a point of a quadric is singular if and only if Equations (9.3)–(9.6) are
satisfied simultaneously, which occurs if and only if det(Q) = 0. A quadric is
said to be singular whenever det(Q) = 0, and non-singular otherwise. Singular
quadrics are cones, cylinders, or a union of planes. Quadrics which are a union
of planes are called reducible, and those which are not are called irreducible.
The determinant
∆ =
abc
bde
cef
is called the discriminant of the quadric, and plays a similar role to the dis-
criminant of a conic by distinguishing the types of quadric. A non-singular
quadric is called a paraboloid, hyperboloid, or ellipsoid according to whether
∆ =0,∆>0, or ∆<0, respectively. The types are further distinguished as
hyperboloids of one or two sheets, and hyperbolic and elliptic paraboloids.
Quadrics for which the axes of rotational symmetry or planes of reflectional
symmetry are aligned with the axes are said to be in normal or standard form.
Any quadric can be mapped to a quadric in normal form by applying three-
dimensional rotations and translations. Space does not permit a detailed dis-
cussion of quadrics. Table 9.1 lists an implicit and a parametric normal form for
each type of irreducible quadric, and the conditions on D =detQ and ∆ which
determine the type. The quadrics are illustrated in the figures on page 231. A
number of quadrics will emerge later in B´ezier and B-spline form in the guise
of surface constructs.
Techniques such as finding the intersection of a quadric with a line, ap-
plying transformations, and converting between parametric and implicit forms
are similar to the corresponding methods for conics. The conversion problem

230 Applied Geometry for Computer Graphics and CAD
Table 9.1 Table of irreducible quadrics
Name Implicit form Parametric form
Ellipsoid
D =0,∆ <0
x
2
a
2
+
y
2
b
2
+
z
2
c
2
=1
(a cos θ sin φ, b sin θ sin φ, c cos φ)
θ ∈ [0, 2π] ,φ ∈ [0,π]
Hyperboloid
(1 sheet)
D =0,∆ >0
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=1
(a cos θ cosh t, b sin θ cosh t, c sinh t)
θ ∈ [0, 2π] ,t ∈ (−∞, ∞)
Hyperboloid
(2 sheets)
D =0,∆ >0
x
2
a
2
+
y
2
b
2
−
z
2
c
2
= −1
(a cos θ sinh t, b sin θ sinh t, ±c cosh t)
θ ∈ [0, 2π] ,t ∈ (−∞, ∞)
Elliptic
paraboloid
D =0,∆ =0
z =
x
2
a
2
+
y
2
b
2
at cos θ, bt sin θ, t
2
θ ∈ [0, 2π] ,t ∈ (−∞, ∞)
Hyperbolic
paraboloid
D =0,∆ =0
z = −
x
2
a
2
+
y
2
b
2
at cosh s, bt sinh s, t
2
s ∈ (−∞, ∞) ,t∈ (−∞, ∞)
Elliptic cone
D =0
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=0
(at cos θ, bt sin θ, ct)
θ ∈ [0, 2π] ,t ∈ (−∞, ∞)
Elliptic
cylinder
D =0
x
2
a
2
+
y
2
b
2
=1
(a cos θ, b sin θ, t)
θ ∈ [0, 2π] ,t ∈ (−∞, ∞)
Parabolic
cylinder
D =0
4ax − y
2
=0
as
2
, 2as, t
s ∈ (−∞, ∞) ,t∈ (−∞, ∞)
requires more space than is available in this text, so the reader is referred to
[23] and [1]. The simpler problems are exemplified below.
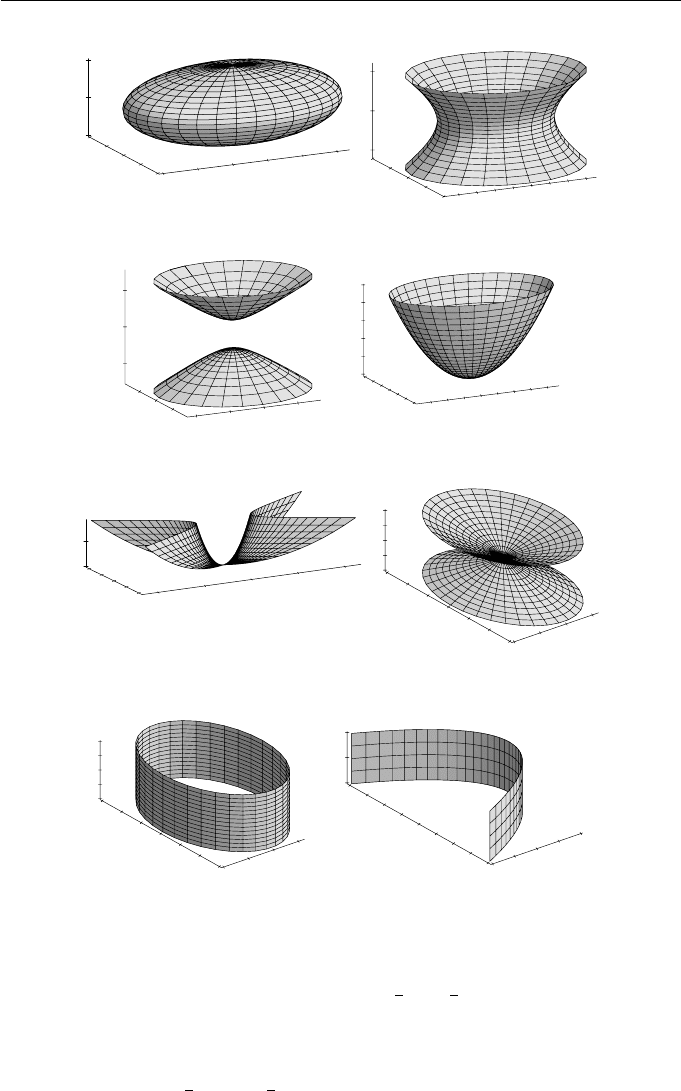
9. Surfaces 231
-2
-1
0
1
2
3
x
2
-1
0
1
2
y
1
0
1
-3
-2
-1
0
1
2
3
4
x
4
-2
0
2
4
y
2
0
2
(a) Ellipsoid (b) Hyperboloid of one sheet
-5
0
5
10
x
-5
0
5
y
5
0
5
-6
-4
-2
0
2
4
6
8
x
6
-4
-2
0
2
4
6
y
0
2
4
6
8
0
(c) Hyperboloid of two sheets (d) Elliptic paraboloid
-20
-10
0
10
20
x
0
-5
0
5
10
y
0
5
-2
0
2
4
x
6
-4
-2
0
2
4
6
y
2
1
0
1
2
(e) Hyperbolic paraboloid (f) Elliptic cone
-1
0
1
2
x
3
-2
-1
0
1
2
3
y
1
0
5
1
0
1
2
3
4
x
-
4
-3
-2
-1
0
1
2
3
4
y
1
0
1
(g) Elliptic cylinder (h) Parabolic cylinder
Example 9.6
The points of intersection of the hyperboloid
1
4
x
2
+
1
9
y
2
−z
2
= −1 and the line
(2t, 3t −2,t+ 3) may be obtained by substituting x =2t, y =3t −2, z = t +3
into the equation of the hyperboloid. This gives
1
4
(2t)
2
+
1
9
(3t − 2)
2
− (t +3)
2
= −1

232 Applied Geometry for Computer Graphics and CAD
which simplifies to t
2
−
22
3
t −
68
9
= 0. The solutions are t =8.2492 and t =
−0.9159. Substituting for t in (2t, 3t −2,t+ 3) yields two points of intersection
(16.4984, 22.7476, 11.2492) and (−1.8318, −4.7477, 2.0841).
Example 9.7
The parametric equation of the quadric obtained when a translation T(3, 5, 4),
followed by a rotation Rot
z
(π/2) about the z-axis, is applied to the elliptic
cylinder S(s, t)=
as
2
, 2as, t
is determined by
as
2
2as t 1
⎛
⎜
⎜
⎝
1000
0100
0010
3541
⎞
⎟
⎟
⎠
⎛
⎜
⎜
⎝
cos
π
2
sin
π
2
00
−sin
π
2
cos
π
2
00
0010
0001
⎞
⎟
⎟
⎠
=
−2as − 5 as
2
+3 t +4 1
.
The transformed quadric is
−2as − 5,as
2
+3,t+4
.
9.2.1 Offset Surfaces
Offset curves were introduced in Section 5.5 in the context of numerical con-
trolled machining. Given a regular surface S(s, t)=(x(s, t),y(s, t),z(s, t)) with
unit normal N(s, t), the offset surface O
d
(s, t)ofS at a distance d is given by
O
d
(s, t)=S(s, t)+d N(s, t) .
Example 9.8
The offset at a distance d of the saddle surface of Example 9.5 is
O
d
(s, t)=(s − t, s + t, s
2
− t
2
)+
d
√
1+2s
2
+2t
2
(−s − t, −s + t, 1) ,
as shown in Figure 9.3.
Offset surfaces have several applications in CAD. First, offset surfaces are used
to obtain paths for NC machining in a similar manner to curves. Second, two
important CAD operations thickening and shelling are achieved by generating
offset surfaces.
Shelling is a hollowing-out operation performed on a solid to give a new
solid that has a thickness of d units. Figure 9.4(a) illustrates a solid bounded
by two circular disks and half of a doughnut-shaped surface called a torus (see
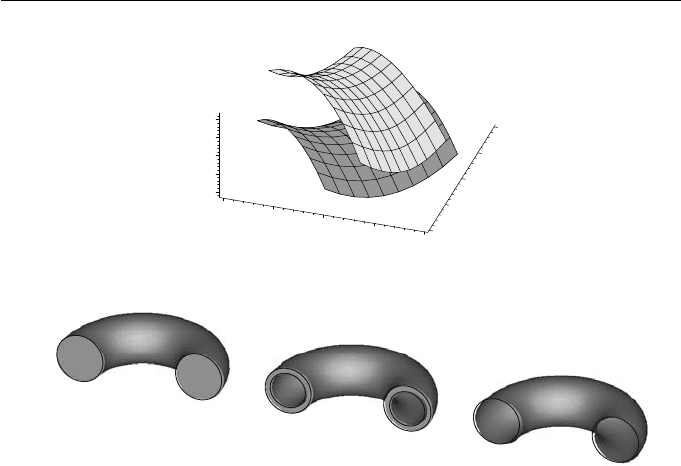
9. Surfaces 233
–
1
–0.5
0
0.5
1
–1
–0.5
0
0.5
1
–0.2
0
0.2
0.4
0.6
Figure 9.3 A surface and an offset
(a) (b) (c)
Figure 9.4 Shelling and thickening operations
Example 9.20). The solid is shelled to give the solid in Figure 9.4(b). The inner
surface bounding the hollow of the solid is an offset surface at a distance d of
the outer torus.
Thickening is the process of transforming a surface into a solid of thickness
d units. Applying the thickening operation to the half-torus of Figure 9.4(c)
results in a solid similar to the the one illustrated in Figure 9.4(b). Note again
that the operation requires the computation of the offset of the torus.
Offset surfaces also arise in the construction of certain types of blend sur-
faces. Blending operations are applied to an object in order to smooth out
sharp edges and vertices. In Figure 9.5(a) a rolling-ball blend smooths the
neighbourhood of a sharp edge of a cube with a pipe or canal surface: that is, a
tubular surface that is the locus of a spherical ball moving along a spine curve.
The radius r of the ball determines the size of the blend. In Figure 9.5(c) a
rolling-ball blend results in material being added to the original model shown in
Figure 9.5(b). The ball is constrained to touch both surfaces during the motion
as shown in Figure 9.6(a). This implies that the centre of the ball is a distance
r from each surface. The spine curve is determined by computing the offset at
a distance r to each of the two surfaces involved in the blend. The spine is the
curve of intersection of the offset surfaces as shown in Figure 9.6(b). In Fig-
ure 9.5 the surfaces and their offsets are planes and so the spine is a line. The
blend surface is obtained by rolling a ball along the line to give a cylindrical

234 Applied Geometry for Computer Graphics and CAD
surface. A further example of a blend can be found in Example 9.20.
(a) (b) (c)
Figure 9.5 Rolling-ball blend
r
r
(a) (b)
Figure 9.6 Construction of the spine for a rolling-ball blend
9.3 B´ezier and B-spline Surfaces
Let B
i,n
(s)andB
j,p
(t) be the Bernstein basis functions of degrees n and p in
the variables s and t, respectively. A B´ezier surface with control points p
i,j
(0 ≤ i ≤ n,0≤ j ≤ p) is the parametric surface defined by
S(s, t)=
n
i=0
p
j=0
p
i,j
B
i,n
(s)B
j,p
(t), for (s, t) ∈ [0, 1] × [0, 1] . (9.7)
The parameter curves of a B´ezier surface are spatial B´ezier curves. In particular,
the parameter curves S(s, 0), S(s, 1), S(0,t), S(1,t), are B´ezier curves which
form the four edges of the B´ezier surface as illustrated in Figure 9.7. A rational
B´ezier surface with control points p
i,j
and weights w
i,j
(0 ≤ i ≤ n,0≤ j ≤ p)
is defined by
S(s, t)=
n
i=0
p
j=0
w
i,j
p
i,j
B
i,n
(s)B
j,p
(t)
n
i=0
p
j=0
w
i,j
B
i,n
(s)B
j,p
(t)
, for (s, t) ∈ [0, 1] × [0, 1] . (9.8)

9. Surfaces 235
Figure 9.7 AB´ezier surface and its control polyhedron
The parameter curves are rational B´ezier curves. The (n +1)×(p + 1) control
points of a B´ezier or rational B´ezier surface form a control point polyhedron.
Let N
i,d
(s) be the B-spline basis functions of degree d with knot vector
s
0
,s
1
,...,s
m
, and let N
j,e
(t) be the B-spline basis functions of degree e with
knot vector t
0
,t
1
,...,t
q
.AB-spline surface with control points p
i,j
(0 ≤ i ≤
n = m − d − 1, 0 ≤ j ≤ p = q − e − 1) is defined by
S(s, t)=
n
i=0
p
j=0
p
i,j
N
i,d
(s)N
j,e
(t), for (s, t) ∈ [s
d
,s
m−d
] × [t
e
,t
q−e
] . (9.9)
A NURBS surface with control points p
i,j
and weights w
i,j
is defined by
S(s, t)=
n
i=0
p
j=0
w
i,j
p
i,j
N
i,d
(s)N
j,e
(t)
n
i=0
p
j=0
w
i,j
N
i,d
(s)N
j,e
(t)
, for (s, t) ∈ [s
d
,s
m−d
] × [t
e
,t
q−e
] .
(9.10)
As for B´ezier surfaces, the (n +1)× (p + 1) control points of a B-spline or
NURBS surface form a control point polyhedron. A B-spline surface is said to
be open (respectively, periodic, closed ) if the basis functions in both s and t
are defined on open (respectively, periodic, closed) knot vectors.
B´ezier or B-spline surfaces are said to be bilinear, biquadratic, bicubic, etc.,
whenever n = p =1,n = p =2,n = p =3,etc.
9.3.1 Properties of B´ezier and B-spline Surfaces
A number of the properties of B´ezier and B-spline surfaces can be deduced in
a similar manner to the corresponding properties for curves. The details are
omitted.

236 Applied Geometry for Computer Graphics and CAD
Theorem 9.9
AB´ezier surface (9.7) satisfies the following properties.
Endpoint Interpolation: S(0, 0) = p
0,0
, S(1, 0) = p
n,0
, S(0, 1) = p
0,p
,
S(1, 1) = p
n,p
.
Convex Hull: S(s, t) ∈ CH{p
0,0
, ..., p
n,p
}, for all (s, t) ∈ [0, 1] × [0, 1].
Invariance under Affine Transformations: Let T be a three-dimensional
affine transformation. Then
T
⎛
⎝
n
i=0
p
j=0
p
i,j
B
i,n
(s)B
j,p
(t)
⎞
⎠
=
n
i=0
p
j=0
T (p
i,j
) B
i,n
(s)B
j,p
(t) .
Theorem 9.10
A rational B´ezier surface (9.8) satisfies the following properties.
Endpoint Interpolation: as for Theorem 9.9.
Convex Hull: If the weights are all positive, then as for Theorem 9.9.
Invariance under Affine Transformations: Let T be a three-dimensional
affine transformation. Then
T
n
i=0
p
j=0
w
i,j
p
i,j
B
i,n
(s)B
j,p
(t)
n
i=0
p
j=0
w
i,j
B
i,n
(s)B
j,p
(t)
=
n
i=0
p
j=0
w
i,j
T (p
i,j
) B
i,n
(s)B
j,p
(t)
n
i=0
p
j=0
w
i,j
B
i,n
(s)B
j,p
(t)
.
Invariance under Projective Transformations:
Let T be a three- dimensional projective transformation, and let
ˆp
i,j
=(w
i,j
x
i,j
,w
i,j
y
i,j
,w
i,j
z
i,j
,w
i,j
)
be the homogeneous control points of p
i,j
=(x
i,j
,y
i,j
,z
i,j
). Then
T
⎛
⎝
n
i=0
p
j=0
ˆp
i,j
B
i,n
(s)B
j,p
(t)
⎞
⎠
=
n
i=0
p
j=0
T (ˆp
i,j
) B
i,n
(s)B
j,p
(t) .
Theorem 9.11
A B-spline surface (9.9) satisfies the following properties.

9. Surfaces 237
Local Control: Each segment is determined by a (d +1)× (e + 1) mesh of
control points. If s ∈ [s
σ
,s
σ+1
)andt ∈ [t
τ
,t
τ+1
)(d ≤ σ ≤ m − d − 1,
e ≤ τ ≤ n − e − 1), then
S(s, t)=
σ
i=σ−d
τ
j=τ −e
p
i,j
N
i,d
(s)N
j,e
(t), for (s, t) ∈ [s
d
,s
m−d
] × [t
e
,t
q−e
] .
Convex Hull:Ifs ∈ [s
σ
,s
σ+1
)andt ∈ [t
τ
,t
τ+1
)(d ≤ σ ≤ m −d −1, e ≤ τ ≤
n − e − 1), then S(s, t) ∈ CH{p
σ−d,τ−e
, ..., p
σ,τ
}.
Invariance under Affine Transformations: Let T be a three-dimensional
affine transformation. Then
T
⎛
⎝
n
i=0
p
j=0
p
i,j
N
i,d
(s)N
j,e
(t)
⎞
⎠
=
n
i=0
p
j=0
T (p
i,j
) N
i,d
(s)N
j,e
(t) .
Theorem 9.12
A NURBS surface (9.10) satisfies the following properties.
Local Control: If s ∈ [s
σ
,s
σ+1
)andt ∈ [t
τ
,t
τ+1
)(d ≤ σ ≤ m − d − 1,
e ≤ τ ≤ n − e − 1), then
S(s, t)=
σ
i=σ−d
τ
j=τ −e
w
i,j
p
i,j
N
i,d
(s)N
j,e
(t)
σ
i=σ−d
τ
j=τ −e
w
i,j
N
i,d
(s)N
j,e
(t)
.
Convex Hull: If the weights w
i
are all positive, then as for Theorem 9.11.
Invariance under Affine Transformations:
Let T be a three-dimensional affine transformation. Then
T
n
i=0
p
j=0
w
i,j
p
i,j
N
i,d
(s)N
j,e
(t)
n
i=0
p
j=0
w
i,j
N
i,d
(s)N
j,e
(t)
=
n
i=0
p
j=0
w
i,j
T (p
i,j
) N
i,d
(s)N
j,e
(t)
n
i=0
p
j=0
w
i,j
N
i,d
(s)N
j,e
(t)
.
Invariance under Projective Transformations:
Let T be a three-dimensional projective transformation, and let ˆp
i,j
=
(w
i,j
x
i,j
,w
i,j
y
i,j
,w
i,j
z
i,j
,w
i,j
) be the homogeneous control points of p
i,j
=
(x
i,j
,y
i,j
,z
i,j
). Then
T
⎛
⎝
n
i=0
p
j=0
ˆp
i,j
N
i,d
(s)N
j,e
(t)
⎞
⎠
=
n
i=0
p
j=0
T (ˆp
i,j
) N
i,d
(s)N
j,e
(t) .
