Marsh D. Applied Geometry for Computer Graphics and CAD
Подождите немного. Документ загружается.

8. B-splines 197
In Example 8.19 it is shown that open B-splines also satisfy
B
(t
d
)=
d
t
d+1
−t
1
(b
1
− b
0
)andB
(t
m−d
)=
d
t
m−1
−t
m−d−1
(b
n
− b
n−1
) . (8.5)
Thus b
0
, b
1
define the initial tangent direction, and b
n−1
, b
n
define the fi-
nal tangent direction of an open B-spline curve. The endpoint interpolation
and endpoint tangent properties imply that open B-splines behave in a similar
manner to B´ezier curves.
Example 8.7
Let t
0
=0,t
1
=0,t
2
=0,t
3
=1,t
4
=2,t
5
=3,t
6
=4,t
7
=4,andt
8
=4.
The k = 0 basis functions are
N
i,0
=
1, if t ∈ [t
i
,t
i+1
)
0, otherwise
.
The k = 1 basis functions are
N
0,1
(t)=
(t−0)
(0−0)
N
0,0
+
(0−t)
(0−0)
N
1,0
= 0 (using the convention 0/0=0),
N
1,1
(t)=
(t−0)
(0−0)
N
1,0
+
(1−t)
(1−0)
N
2,0
=(1− t)N
2,0
(t) (using 0/0=0),
N
2,1
(t)=
(t−0)
(1−0)
N
2,0
+
(2−t)
(2−0)
N
3,0
= tN
2,0
(t)+(2− t)N
3,2
(t) ,
N
3,1
(t)=
(t−1)
(2−1)
N
3,0
+
(3−t)
(3−1)
N
4,0
=(t − 1)N
3,0
(t)+(3− t)N
4,0
(t) ,
N
4,1
(t)=
(t−2)
(3−2)
N
4,0
+
(4−t)
(4−2)
N
5,0
=(t − 2)N
4,0
(t)+(4− t)N
5,0
(t) ,
N
5,1
(t)=
(t−3)
(4−3)
N
5,0
+
(4−t)
(4−4)
N
6,0
=(t − 3)N
5,0
(using 0/0=0),
N
6,1
(t)=
(t−4)
(4−4)
N
6,0
+
(4−t)
(4−4)
N
7,0
=0 (using0/0=0).
The k = 2 basis functions are
N
0,2
(t)=(1− t)
2
N
2,0
(t) ,
N
1,2
(t)=
1
2
(4 − 3t)tN
2,0
(t)+
1
2
(2 − t)
2
N
3,0
(t) ,
N
2,2
(t)=
1
2
t
2
N
2,0
(t)+(−t
2
+3t −
3
2
)N
3,0
+(
9
2
− 3t +
1
2
t
2
)N
4,0
,
N
3,2
(t)=
1
2
(t − 1)
2
N
3,0
(t)+(−
11
2
+5t − t
2
)N
4,0
+(8− 4t +
1
2
t
2
)N
5,0
,
N
4,2
(t)=
1
2
(t − 2)
2
N
4,0
(t)+(−16 + 10t −
3
2
t
2
)N
5,0
,
N
5,2
(t)=(t − 3)
2
N
5,0
(t) .
An open B-spline of degree d = 2, defined on the given knot vector, consists of
the four segments
B
1
(t)=(1− t)
2
b
0
+
1
2
t(4 − 3t)b
1
+
1
2
t
2
b
2
,t∈ [0, 1] ,
B
2
(t)=
1
2
(2 − t)
2
b
1
+
1
2
(−2t
2
+6t − 3)b
2
+
1
2
(t − 1)
2
b
3
,t∈ [1, 2] ,
B
3
(t)=
1
2
(3 − t)
2
b
2
+
1
2
(−2t
2
+10t − 11)b
3
+
1
2
(t − 2)
2
b
4
,t∈ [2, 3] ,
B
4
(t)=
1
2
(4 − t)
2
b
3
+
1
2
(−3t
2
+20t − 32)b
4
+(t − 3)
2
b
5
,t∈ [3, 4] .

198 Applied Geometry for Computer Graphics and CAD
Note that B(0) = b
0
and B(4) = b
5
, and hence the B-spline interpolates the
first and last control points.
EXERCISES
8.1. Let t
0
=0,t
1
=1,t
2
=2,t
3
=3,t
4
=4,t
5
=5,andt
6
= 6. Deter-
mine the basis functions for a B-spline of degree 2. Use the method
of Examples 8.3 and 8.4 to obtain the equations of the segments of
a B-spline of degree 2 defined on this knot vector.
8.2. Let t
0
=0,t
1
=1,t
2
=2,t
3
=3,t
4
=4,t
5
=5,t
6
=6,t
7
=7.
Determine the basis functions required for a B-spline of degree 3.
(The results of the previous exercise are useful!) Obtain the segments
of a B-spline of degree 3 defined on this knot vector.
8.3. Let t
0
=0,t
1
=0,t
2
=0,t
3
=1,t
4
=2,t
5
=3,t
6
=3,andt
7
=3.
Determine the segments of an open B-spline of degree 2 defined on
this knot vector.
8.4. The open cubic B-spline with knot vector t
0
= t
1
= t
2
= t
3
=0
and t
4
= t
5
= t
6
= t
7
= 1 has just one segment which satisfies the
endpoint conditions. Determine the basis functions, and show that
the open B-spline is a cubic B´ezier curve.
Uniform B-splines
AB-splineissaidtobeuniform whenever its knots are equally spaced, and
non-uniform otherwise. Let the knot vector be t
0
=0,t
1
=1,t
2
=2,...,t
m
=
m. The basis functions for the uniform B-spline of degree 2 on this knot vector
are obtained as follows:
N
i,0
(t)=
1, if t ∈ [t
i
,t
i+1
)
0, otherwise
.
N
0,1
(t)=
(t−0)
(1−0)
N
0,0
+
(2−t)
(2−1)
N
1,0
= tN
0,0
+(2− t)N
1,0
,
N
1,1
(t)=
(t−1)
(2−1)
N
1,0
+
(3−t)
(3−2)
N
2,0
=(t − 1) N
1,0
+(3− t)N
2,0
,
N
2,1
(t)=
(t−2)
(3−2)
N
2,0
+
(4−t)
(4−3)
N
3,0
=(t − 2) N
2,0
+(4− t)N
3,0
.
8. B-splines 199
N
0,2
(t)=
(t−0)
(2−0)
N
0,1
(t)+
(3−t)
(3−1)
N
1,1
(t)=
1
2
tN
0,1
(t)+
1
2
(3 − t)N
1,1
(t)
=
1
2
t (tN
0,0
+(2− t)N
1,0
)+
1
2
(3 − t)((t − 1)N
1,0
+(3− t)N
2,0
)
=
1
2
t
2
N
0,0
+
1
2
t(2 − t)+
1
2
(3 − t)(t − 1)
N
1,0
+
1
2
(3 − t)
2
N
2,0
=
⎧
⎨
⎩
1
2
t
2
,t∈ [0, 1]
−
1
2
3 − 6t +2t
2
,t∈ [1, 2]
1
2
(3 − t)
2
,t∈ [2, 3]
.
The ith basis function is
N
i,2
(t)=
t−i
(i+2)−i
N
i,1
(t)+
i+3−t
(i+3)−(i+1)
N
i+1,1
(t)
=
t−i
2
N
i,1
(t)+
i+3−t
2
N
i+1,1
(t)
=
t−i
2
t−i
(i+1)−i
N
i,0
(t)+
(i+2)−t
(i+2)−(i+1)
N
i+1,0
(t)
+
i+3−t
2
t−(i+1)
(i+2)−(i+1)
N
i+1,0
(t)+
i+3−t
(i+3)−(i+2)
N
i+2,0
(t)
=
1
2
(t − i)
2
N
i,0
(t)
+
1
2
((t − i)(i +2− t)+(i +3− t)(t − i − 1)) N
i+1,0
(t)
+
1
2
(i +3− t)
2
N
i+2,0
(t) .
Thus the ith segment B
i
(t), defined on [i +2,i+ 3), is given by
B
i
(t)=
i+2
j=i
b
j
N
j,2
(t)
=
1
2
(i +3− t)
2
b
i
+
1
2
((t − i − 1)(i +3− t)+(i +4− t)(t − i − 2)) b
i+1
+
1
2
(t − i − 2)
2
b
i+2
.
Finally, the reparametrization t → t + i + 2 defines the segment on the interval
[0, 1] by
B
i
(t)=
1
2
(1 − t)
2
b
i
+
1
2
(1 + 2t − 2t
2
)b
i+1
+
1
2
t
2
b
i+2
(8.6)
=
1
2
t
2
t 1
⎛
⎝
1 −21
−220
110
⎞
⎠
⎛
⎝
b
i
b
i+1
b
i+2
⎞
⎠
.
Points on each segment are efficiently computed since the basis functions
1
2
(1 − t)
2
,
1
2
(1 + 2t − 2t
2
),
1
2
t
2
have only to be evaluated once for each t.
For uniform B-splines of degree d = 3, a similar method gives
B
i
(t)=
1
6
t
3
t
2
t 1
⎛
⎜
⎜
⎝
−13−31
3 −630
−3030
1410
⎞
⎟
⎟
⎠
⎛
⎜
⎜
⎝
b
i
b
i+1
b
i+2
b
i+3
⎞
⎟
⎟
⎠
.

200 Applied Geometry for Computer Graphics and CAD
Example 8.8
Consider the uniform B-spline B(t)ofdegreed = 2 defined on the knot vector
t
0
=0,t
1
=1,t
2
=2,t
3
=3,t
4
=4,t
5
=5,t
6
=6,t
7
= 7, and with control
points b
0
(3, 2), b
1
(7, −1), b
2
(5, 2), b
3
(4, 5), b
4
(2, 3). The curve is defined on
the interval [t
d
,t
m−d
]=[2, 5]. There are three curve segments defined on the
sub-intervals [2, 3], [3, 4], and [4, 5]. For instance, to determine the point B(3.6)
which lies on the i = 1 segment, t =3.6 is translated into the interval [0, 1]
using t → t − i − 2. The required parameter is t =3.6 − 1 − 2=0.6, and (8.6)
gives
B
1
(0.6) =
1
2
(1 − 0.6)
2
(7, −1) +
1
2
(1 + 2(0.6) − 2(0.6)
2
)(5, 2) +
1
2
(0.6)
2
(4, 5)
=(4.98, 2.3) .
Periodic B-splines and Closed Periodic B-splines
In a number of applications, it is desirable to represent closed curves for
which the starting point equals the finishing point. A closed B´ezier curve can
be obtained by choosing control points which form a closed control polygon.
But, in general, B-splines do not interpolate the first and last control points,
and therefore a closed control polygon does not yield a closed curve. Closure of
the curve is obtained by imposing conditions on the control points and knots.
For instance, an open B-spline could be used for this purpose. An alternative
is to use a closed periodic B-spline.
A periodic B-spline of degree d and with n + 1 control points is obtained by
choosing knots t
0
≤ ...≤ t
n
arbitrarily, and then setting
t
n+i
= t
n+i−1
+(t
i
− t
i−1
) ,
for i =1,...,d+ 1. A knot vector of this form is called a periodic knot vector.
In particular, a uniform B-spline is a special case of a periodic B-spline.
A closed periodic B-spline of degree d and control points b
0
,...,b
n
, b
n+1
=
b
0
, b
n+2
= b
1
,...,b
n+d
= b
d−1
is obtained by choosing knots t
0
≤ ...≤ t
n+1
arbitrarily, and forming a periodic knot vector with n +2d + 2 knots.
Example 8.9
Let d = 3 and n = 4. Let the first five control points be b
0
(1, 2), b
1
(3, 7),
b
2
(6, 6), b
3
(6, −2), b
4
(1, −1), and let the remaining control points be b
5
(1, 2),
b
6
(3, 7), b
7
(6, 6). Suppose the first n + 2 = 6 knots are t
0
=0.0, t
1
=0.5,
t
2
=2.0, t
3
=3.0, t
4
=3.1, t
5
=3.4. The periodic knot vector is obtained by
8. B-splines 201
taking
t
6
=3.4+(0.5 − 0.0) = 3.9 ,t
7
=3.9+(2.0 − 0.5) = 5.4 ,
t
8
=5.4+(3.0 − 2.0) = 6.4 ,t
9
=6.4+(3.1 − 3.0) = 6.5 ,
t
10
=6.5+(3.4 − 3.1) = 6.8 ,t
11
=6.8+(5.4 − 3.9) = 8.3 .
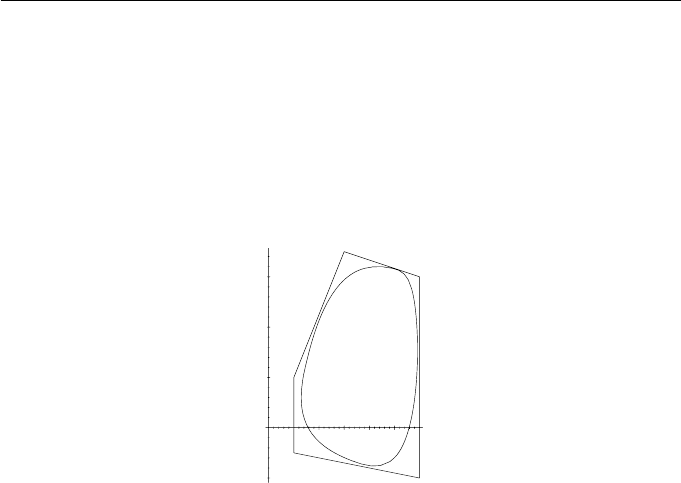
The B-spline and its control polygon are illustrated in Figure 8.4.
-2
0
2
4
6
1234
5
6
Figure 8.4 Closed periodic B-spline of degree 3
EXERCISES
8.5. Evaluate the uniform B-spline of Example 8.8 at t =2.5andt =4.2.
8.6. Let d =3,andb
0
(0, 0), b
1
(2, 0), b
2
(4, 2), b
3
(2, 4), b
4
(0, 2). Suppose
the first knots are t
0
=0,t
1
=1,t
2
=2,t
3
=3,t
4
=4,t
5
=5.
Compute the knots and control points required to form a closed
B-spline curve.
8.7. Let d =3,andb
0
(3, 5), b
1
(4, 8), b
2
(7, 2), b
3
(6, −3), b
4
(3, −1). Sup-
pose the first knots are t
0
=0.3, t
1
=0.4, t
2
=1.3, t
3
=2.5, t
4
=2.9,
t
5
=3.7. Compute the knots and control points required to form a
closed B-spline curve.
202 Applied Geometry for Computer Graphics and CAD
Open Uniform B-splines
Open B-splines for which the interior knots are uniform are referred to as
open uniform B-splines. Example 8.7 is an open uniform B-spline.
Example 8.10
Let t
0
=0,t
1
=0,t
2
=0,t
3
=1,t
4
=2,t
5
=3,t
6
=3,andt
7
= 3. The basis
functions for open uniform B-splines of degree 2 defined on this knot vector are
N
0,2
=
⎧
⎨
⎩
0,t<0
(t − 1)
2
, 0 ≤ t<1
0, 1 ≤ t
,
N
1,2
=
⎧
⎪
⎪
⎨
⎪
⎪
⎩
0,t<0
2t −
3
2
t
2
, 0 ≤ t<1
3
2
− t +
1
2
(t − 1)
2
, 1 ≤ t<2
0, 2 ≤ t
,
N
2,2
=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
0,t<0
1
2
t
2
, 0 ≤ t<1
−
1
2
+ t − (t − 1)
2
, 1 ≤ t<2
5
2
− t +
1
2
(t − 2)
2
, 2 ≤ t<3
0, 3 ≤ t
,
N
3,2
=
⎧
⎪
⎪
⎨
⎪
⎪
⎩
0,t<1
1
2
(t − 1)
2
, 1 ≤ t<2
−
3
2
+ t −
3
2
(t − 2)
2
, 2 ≤ t<3
0, 3 ≤ t
,
N
4,2
=
⎧
⎨
⎩
0,t<2
(t − 2)
2
, 2 ≤ t<3
0, 3 ≤ t
.
EXERCISES
8.8. Let t
0
=0,t
1
=0,t
2
=0,t
3
=2,t
4
=4,t
5
=6,t
6
=8,t
7
=8,
t
8
= 8. Obtain the basis functions for open uniform B-splines of
degree 2 defined on this knot vector.
8.9. Let t
0
=0,t
1
=0,t
2
=0,t
3
=0,t
4
=1,t
5
=2,t
6
=3,t
7
=4,
t
8
=4,t
9
=4,t
10
= 4. Obtain the basis functions for open uniform
B-splines of degree 3 defined on this knot vector.
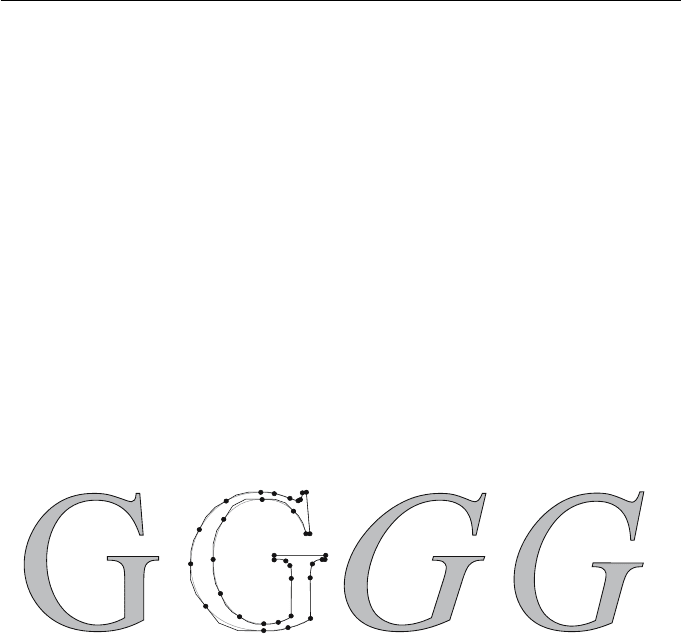
8. B-splines 203
8.10. Use a computer package to plot the cubic open uniform B-spline
defined on the knot vector of Exercise 8.8 with control points (2, 4),
(−2, 4), (−2, 0), (0, 0), (2, 0), (2, −4), (−2, −4).
8.1.3 Application: Font Design
An interesting application of B-splines is to font design. The boundary of each
character in a font is specified by B-spline (or B´ezier) curves. Figures 8.5(a) and
(b) show a letter ‘G’ together with its defining control polygons. Different font
sizes are obtained by applying scaling transformations to the control points, and
making use of the property of invariance under affine transformations. Italic
fonts may be obtained by applying a shear transformation (Figure 8.5(c)) or
a projection (Figure 8.5(d)). Projections of B-splines are discussed in Section
8.2.1. The B-spline data required to store the font definition is considerably
less than, for instance, storing a bitmap representation for each character.
(a) (b) (c) (d)
Figure 8.5 B-spline font definition
8.1.4 Application: Morphing or Soft Object Animation
Morphing is a technique used in computer graphics in which a shape is grad-
ually deformed over an period of time. Morphing has been used in animation
sequences of feature films. In practice, morphing can involve a number of ad-
vanced computational methods including surface deformation, surface render-
ing, and texture mapping. In this section the process of deformation is exempli-
fied by a simple version of the technique where the initial and final shapes are
B-spline curves (including B´ezier curves as a special case). It is assumed that
the B-splines have the same degree and knot vector, though these restrictions
can be removed by applying knot insertion (Section 8.3) and degree raising
algorithms [13].
204 Applied Geometry for Computer Graphics and CAD
Let B(t)andC(t) be B-splines of degree d with control points b
0
,...,b
n
and c
0
,...,c
n
respectively, and defined on the knot vector t
0
,...,t
m
.
Definition 8.11
An N-step deformation of B(t)intoC(t) is a sequence of B-splines D
0
(t), D
1
(t),
...,D
N
(t) such that D
0
(t)=B(t)andD
N
(t)=C(t).
The N +1 curves D
k
(t)(k =0,...,N+1) are the “in-between” curves which
define the gradual change from curve B into curve C. In order to describe a
deformation it is sufficient to prescribe the control points d
k
0
,...,d
k
n
of D
k
(t).
A linear N-step deformation D
k
(t)isgivenby
d
k
i
= b
i
+
k
N
(c
i
− b
i
)fork =0,...,N . (8.7)
Thus d
0
i
= b
i
and d
N
i
= c
i
.
Example 8.12
Let the control points of a curve B(t)beb
0
(1, 0), b
1
(0, 0), b
2
(−1, 5), b
3
(1, 3),
b
4
(3, 5), b
5
(2, 0), b
6
(1, 0), and the control points of a curve C(t)bec
0
(1, 0),
c
1
(−3, 1), c
2
(−4, 5), c
3
(1, 4), c
4
(6, 5), c
5
(5, 1), c
6
(1, 0). Let t
0
= ···= t
6
=0
and t
7
= ···= t
13
= 1. Then both B-splines are B´ezier curves of degree 6 and
d
k
0
=(1, 0) + ((1, 0) − (1, 0))
k
N
=(1, 0) ,
d
k
1
=(0, 0) + ((−3, 1) − (0, 0))
k
N
=
−3k
N
,
k
N
,
d
k
2
=(−1, 5) + ((−4, 5) − (−1, 5))
k
N
=
−1 −
3k
N
, 5
,
d
k
3
=(1, 3) + ((1, 4) − (1, 3))
k
N
=
1, 3+
k
N
,
d
k
4
=(3, 5) + ((6, 5) − (3, 5))
k
N
=
3+
3k
N
, 5
,
d
k
5
=(2, 0) + ((5, 1) − (2, 0))
k
N
=
2+
3k
N
,
k
N
,
d
k
6
=(1, 0) + ((1, 0) − (1, 0))
k
N
=(1, 0) .
The in-between curves for N = 4 are shown in Figure 8.6. More general
deformations can be obtained by replacing
k
N
in (8.7) by more general functions
of k. For example, let λ
i,k
(s) be continuous functions such that λ
i,0
(0) = 0,
λ
i,N
(1) = 1. Then a deformation D
i
(t)isgivenby
d
k
i
= b
i
+ λ
i,k
k
N
(c
i
− b
i
)fork =0,...,N . (8.8)
Exercise 8.11
Implement the B-spline deformation given by (8.8). Experiment with
different choices of functions λ
i,k
(s).
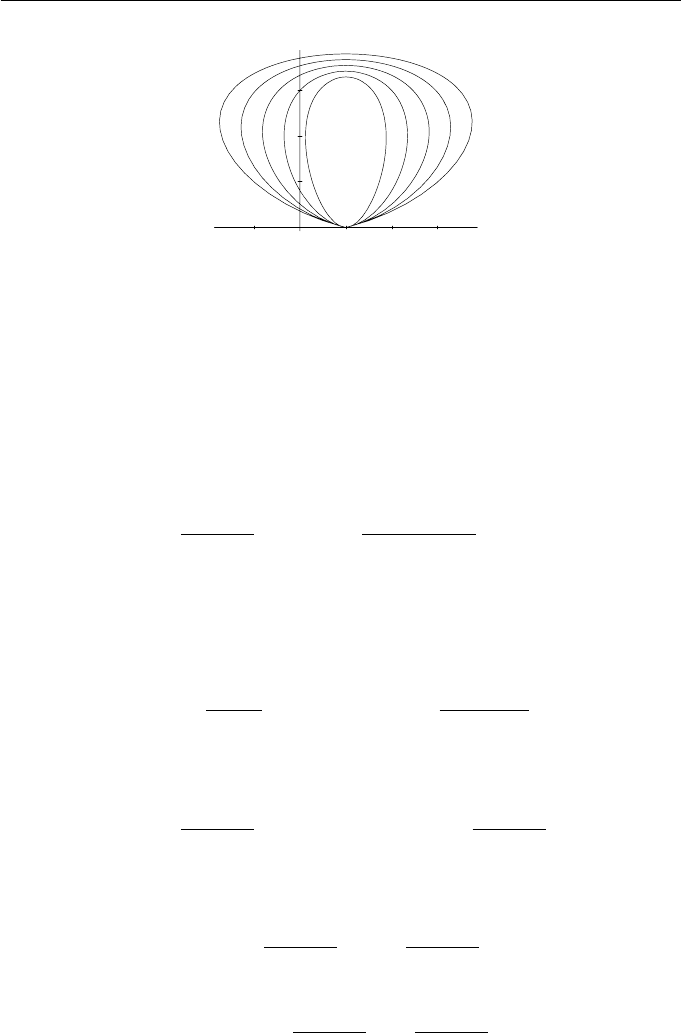
8. B-splines 205
0
1
2
3
-1 1 2 3
Figure 8.6 Linear deformation of a B-spline curve
8.1.5 The de Boor Algorithm
Evaluations of points on a B-spline curve can be performed using a method
known as the de Boor algorithm. Just as the de Casteljau algorithm for B´ezier
curves is a consequence of the recursive property of the Bernstein basis func-
tions, the de Boor algorithm follows from the recursion property of the B-spline
basis functions
N
i,k
(t)=
t − t
i
t
i+k
− t
i
N
i,k−1
(t)+
t
i+k+1
− t
t
i+k+1
− t
i+1
N
i+1,k−1
(t) . (8.9)
Suppose t ∈ [t
r
,t
r+1
). Then (8.9) implies
B(t)=
r
i=r−k
b
i
N
i,k
(t)
=
r
i=r−k
b
i
t−t
i
t
i+k
−t
i
N
i,k−1
(t)+
r
i=r−k
b
i
t
i+k+1
−t
t
i+k+1
−t
i+1
N
i+1,k−1
(t) .
Replacing i by i − 1 in the second sum gives
B(t)=
r
i=r−k
b
i
t − t
i
t
i+k
− t
i
N
i,k−1
(t)+
r+1
i=r−k+1
b
i−1
t
i+k
− t
t
i+k
− t
i
N
i,k−1
(t) ,
and since N
r+1,k−1
(t)=N
r−k,k−1
(t)=0on[t
r
,t
r+1
),
B(t)=
r
i=r−k+1
b
i
t − t
i
t
i+k
− t
i
+ b
i−1
t
i+k
− t
t
i+k
− t
i
N
i,k−1
(t) .
Let
b
1
i
(t)=b
i−1
t
i+k
− t
t
i+k
− t
i
+ b
i
t − t
i
t
i+k
− t
i
,
for i = r − k +1,...,r. Note that b
1
i
is dependent on the parameter value t.
In a similar manner, N
i,k−1
(t) can be expressed in terms of the basis functions

206 Applied Geometry for Computer Graphics and CAD
of degree k − 2 and so on. For a curve of degree d, the result is a recursive
procedure
b
j
i
(t)=(1− α
j
i
(t))b
j−1
i−1
(t)+α
j
i
(t)b
j−1
i
(t) ,
α
j
i
(t)=
t − t
i
t
i+d−j+1
− t
i
,
⎫
⎬
⎭
(8.10)
for j =1,...,d, i = r−d+j,...,r,whereb
0
j
(t)=b
j
, b
−1
= 0,andb
m−d+1
= 0
(where 0 denotes (0, 0) for a plane curve and (0, 0, 0) for a spatial curve). The
j
th
step yields B(t) in terms of the basis functions of degree d − j (note b
j
i
is
a function of t)
B(t)=
r
i=r−d+j
b
j
i
N
i,d−j
(t) .
Thus when j = d, the algorithm yields the point B(t)=
r
i=r
b
d
i
N
i,0
(t)=b
d
r
on the curve.
To summarize, for a given parameter value t, the de Boor algorithm (8.10)
yields a triangular array of points such that b
d
r
= B(t).
b
0
r−d
b
0
r−d+1
... ... b
0
r
b
1
r−d+1
... ... b
1
r
.
.
. ...
b
d−1
r−1
b
d−1
r
b
d
r
= B(t) .
Example 8.13
The de Boor algorithm can be applied to evaluate the uniform B-spline of
Example 8.8 at t =3.6. Then d = 2, and since 3.6 ∈ [3, 4) = [t
3
,t
4
), it
follows that r = 3. The first row of points is b
0
1
(7, −1), b
0
2
(5, 2), b
0
3
(4, 5). The
algorithm with j =1...2, i =(1+j) ...3, yields
α
1
2
=
t − t
2
t
4
− t
2
=
3.6 − 2
4 − 2
=0.8,α
1
3
=
t − t
3
t
5
− t
3
=
3.6 − 3
5 − 3
=0.3 ,
α
2
3
=
t − t
3
t
4
− t
3
=
3.6 − 3
4 − 3
=0.6 ,
b
1
2
=(1− 0.8) (7, −1) + 0.8(5, 2) = (5.4, 1.4) ,
b
1
3
=(1− 0.3) (5, 2) + 0.3(4, 5) = (4.7, 2.9) ,
b
2
3
=(1− 0.6) (5.4, 1.4) + 0.6(4.7, 2.9) = (4.98, 2.3) .
Hence B(3.6) = (4.98, 2.3) verifying the result of Example 8.8.
