Marsh D. Applied Geometry for Computer Graphics and CAD
Подождите немного. Документ загружается.

8
B-splines
8.1 Integral B-spline Curves
A piecewise polynomial curve has a B-spline basis representation with proper-
ties similar to those of a B´ezier curve. A B-spline curve defined on the interval
[a, b] is specified by the following information:
1. The degree d (or order d + 1), so that each segment of the piecewise poly-
nomial curve has degree d or less.
2. A sequence of m + 1 real numbers t
0
,t
1
,...,t
m
, called the knot vector,
such that t
i
≤ t
i+1
(i =0,...,m− 1), t
d
= a and t
m−d
= b. The knots
t
0
,t
1
, ..., t
d
and t
m−d
,t
m−d+1
,...,t
m
are called end knots, and the knots
t
d+1
,t
d+2
, ..., t
m−d−1
are called interior knots.
3. Control points b
0
,...,b
n
.
A B-spline curve is defined in terms of B-spline basis functions.
Definition 8.1
The B-spline basis functions of degree d, denoted N
i,d
(t), defined by the knot
187

188 Applied Geometry for Computer Graphics and CAD
vector t
0
,t
1
,...,t
m
are defined recursively as follows:
N
i,0
(t)=
1, if t ∈ [t
i
,t
i+1
)
0, otherwise
, (8.1)
N
i,d
(t)=
t − t
i
t
i+d
− t
i
N
i,d−1
(t)+
t
i+d+1
− t
t
i+d+1
− t
i+1
N
i+1,d−1
(t) , (8.2)
for i =0,...,n and d ≥ 1. If the knot vector contains a sufficient number
of repeated knot values, then a division of the form N
i,d−1
(t)/ (t
i+d
− t
i
)=
0/0 (for some i) may be encountered during the execution of the recursion.
Whenever this occurs, it is assumed that 0/0=0.
Definition 8.2
The B-spline curve of degree d (or order d + 1) with control points b
0
, ..., b
n
and knots t
0
, ..., t
m
is defined on the interval [a, b]=[t
d
,t
m−d
]by
B(t)=
n
i=0
b
i
N
i,d
(t) ,
where N
i,d
(t) are the B-spline basis functions of degree d. To distinguish B-
spline curves from their rational form (which will be introduced in Section 8.2)
they are often referred to as integral B-splines.
Example 8.3
Let d =2,andt
0
=2,t
1
=4,t
2
=5,t
3
=7,t
4
=8,t
5
= 10, t
6
= 11,
with control points b
0
(1, 2), b
1
(3, 5), b
2
(6, 2), b
3
(9, 4). Then the k =0basis
functions are
N
0,0
(t)=
1, if t ∈ [2, 4)
0, otherwise
,N
1,0
(t)=
1, if t ∈ [4, 5)
0, otherwise
,
N
2,0
(t)=
1, if t ∈ [5, 7)
0, otherwise
,N
3,0
(t)=
1, if t ∈ [7, 8)
0, otherwise
,
N
4,0
(t)=
1, if t ∈ [8, 10)
0, otherwise
,N
5,0
(t)=
1, if t ∈ [10, 11)
0, otherwise
.
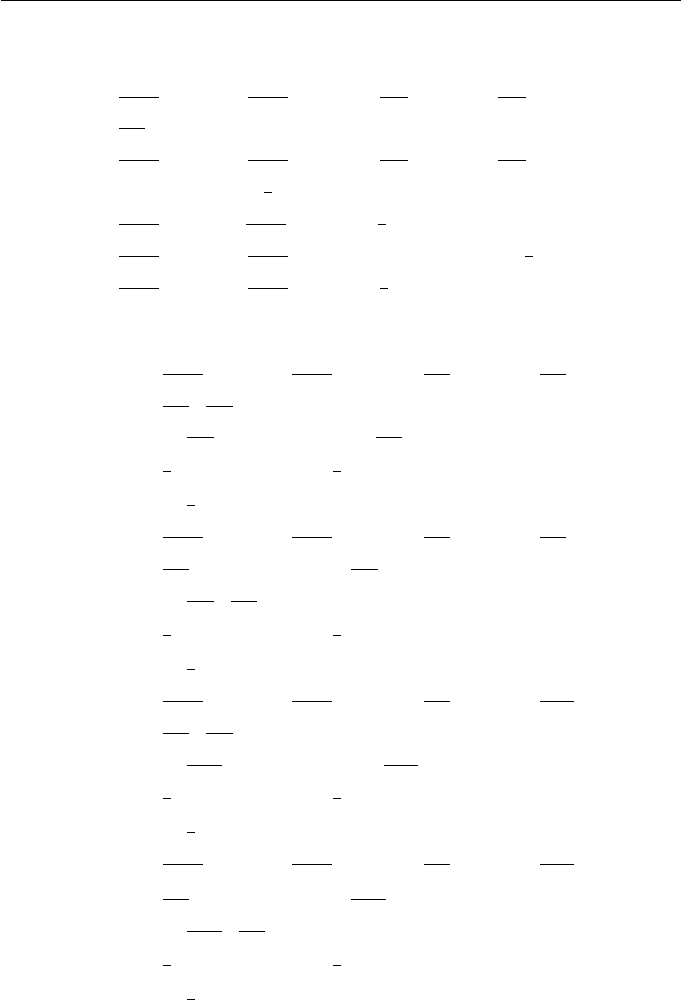
8. B-splines 189
The k = 1 basis functions are determined in terms of these
N
0,1
(t)=
t−t
0
t
1
−t
0
N
0,0
(t)+
t
2
−t
t
2
−t
1
N
1,0
(t)=
t−2
4−2
N
0,0
(t)+
5−t
5−4
N
1,0
(t)
=
t−2
2
N
0,0
(t)+(5− t) N
1,0
(t) ,
N
1,1
(t)=
t−t
1
t
2
−t
1
N
1,0
(t)+
t
3
−t
t
3
−t
2
N
2,0
(t)=
t−4
5−4
N
1,0
(t)+
7−t
7−5
N
2,0
(t)
=(t − 4) N
1,0
(t)+
1
2
(7 − t) N
2,0
(t) ,
N
2,1
(t)=
t−t
2
t
3
−t
2
N
i,0
(t)+
t
4
−t
t
4
−t
3
N
3,0
(t)=
1
2
(t − 5) N
2,0
(t)+(8− t) N
3,0
(t) ,
N
3,1
(t)=
t−t
3
t
4
−t
3
N
3,0
(t)+
t
5
−t
t
5
−t
4
N
4,0
(t)=(t − 7) N
3,0
(t)+
1
2
(10 − t) N
4,0
(t) ,
N
4,1
(t)=
t−t
4
t
5
−t
4
N
4,0
(t)+
t
6
−t
t
6
−t
5
N
5,0
(t)=
1
2
(t − 8) N
4,0
(t)+(11− t) N
5,0
(t) .
Finally, the k = 2 basis functions can be computed
N
0,2
(t)=
t−t
0
t
2
−t
0
N
0,1
(t)+
t
3
−t
t
3
−t
1
N
1,1
(t)=
t−2
3
N
0,1
(t)+
7−t
3
N
1,1
(t)
=
t−2
3
t−2
2
N
0,0
(t)+(5− t) N
1,0
(t)
+
7−t
3
(t − 4) N
1,0
(t)+
7−t
2
N
2,0
(t)
=
1
6
(t − 2)
2
N
0,0
(t)+
1
3
−2t
2
+18t − 38
N
1,0
(t)
+
1
6
(7 − t)
2
N
2,0
(t) ,
N
1,2
(t)=
t−t
1
t
3
−t
1
N
1,1
(t)+
t
4
−t
t
4
−t
2
N
2,1
(t)=
t−4
3
N
1,1
(t)+
8−t
3
N
2,1
(t)
=
t−4
3
(t − 4) N
1,0
(t)+
7−t
2
N
2,0
(t)
+
8−t
3
t−5
2
N
2,0
(t)+(8− t) N
3,0
(t)
=
1
3
(t − 4)
2
N
1,0
(t)+
1
3
−t
2
+12t − 34
N
2,0
(t)
+
1
3
(8 − t)
2
N
3,0
(t) ,
N
2,2
(t)=
t−t
2
t
4
−t
2
N
2,1
(t)+
t
5
−t
t
5
−t
3
N
3,1
(t)=
t−5
3
N
2,1
(t)+
10−t
3
N
3,1
(t)
=
t−5
3
t−5
2
N
2,0
(t)+(8− t) N
3,0
(t)
+
10−t
3
(t − 7) N
3,0
(t)+
10−t
2
N
4,0
(t)
=
1
6
(t − 5)
2
N
2,0
(t)+
1
3
−2t
2
+30t − 110
N
3,0
(t)
+
1
6
(10 − t)
2
N
4,0
(t) ,
N
3,2
(t)=
t−t
3
t
5
−t
3
N
3,1
(t)+
t
6
−t
t
6
−t
4
N
4,1
(t)=
t−7
3
N
3,1
(t)+
11−t
3
N
4,1
(t)
=
t−7
3
(t − 7) N
3,0
(t)+
10−t
2
N
4,0
(t)
+
11−t
3
t−8
2
N
4,0
(t)+(11− t) N
5,0
(t)
=
1
3
(t − 7)
2
N
3,0
(t)+
1
3
−t
2
+18t − 79
N
4,0
(t)
+
1
3
(11 − t)
2
N
5,0
(t) .
190 Applied Geometry for Computer Graphics and CAD
NNNNN
4,13,12,11,10,1
0
1
1234
5
6
7
8 9 10 11 12
t
Figure 8.1 Basis functions of degree 1 for the knot vector t
0
=2,t
1
=4,
t
2
=5,t
3
=7,t
4
=8,t
5
= 10, t
6
=11
The k = 2 basis functions may be expressed in the form
N
0,2
(t)=
⎧
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎩
0,t<2
1
6
(t − 2)
2
, 2 ≤ t<4
1
3
−2t
2
+18t − 38
, 4 ≤ t<5
1
6
(7 − t)
2
, 5 ≤ t<7
0, 7 ≤ t
,
N
1,2
(t)=
⎧
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎩
0,t<4
1
3
(t − 4)
2
, 4 ≤ t<5
1
3
−t
2
+12t − 34
, 5 ≤ t<7
1
3
(8 − t)
2
, 7 ≤ t<8
0, 8 ≤ t
,
N
2,2
(t)=
⎧
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎩
0,t<5
1
6
(t − 5)
2
, 5 ≤ t<7
1
3
−2t
2
+30t − 110
, 7 ≤ t<8
1
6
(10 − t)
2
, 8 ≤ t<10
0, 10 ≤ t
, and
N
3,2
(t)=
⎧
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎩
0,t<7
1
3
(t − 7)
2
, 7 ≤ t<8
1
3
−t
2
+18t − 79
, 8 ≤ t<10
1
3
(11 − t)
2
, 10 ≤ t<11
0, 11 ≤ t
.
Plots of the degree 1 and 2 basis functions are shown in Figures 8.1 and 8.2.
Observe that the basis functions satisfy N
i,2
(t) > 0fort ∈ (t
i
,t
i+3
)and
N
i,2
(t) = 0 elsewhere. General B-spline basis functions satisfy similar “posi-
tivity” and “local support” properties (see Theorem 8.5). The B-spline curve
8. B-splines 191
N
N
N
N
3,2
2,2
1,2
0,2
0
1
1234
5
6
7
8 9 10 11 12
t
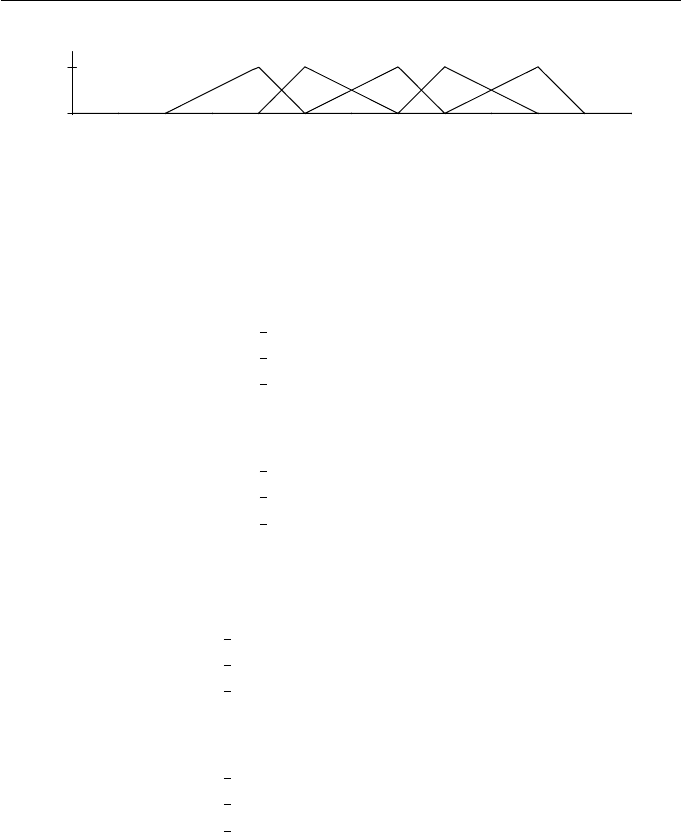
Figure 8.2 Basis functions of degree 2 for the knot vector t
0
=2,t
1
=4,
t
2
=5,t
3
=7,t
4
=8,t
5
= 10, t
6
=11
is defined on the interval [5, 8] by
B(t)=(1, 2)N
0,2
(t)+(3, 5)N
1,2
(t)+(6, 2)N
2,2
(t)+(9, 4)N
3,2
(t)
=
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
1
6
(7 − t)
2
(1, 2) +
1
3
−t
2
+12t − 34
(3, 5)
+
1
6
(t − 5)
2
(6, 2),
if 5 ≤ t<7,
1
3
(8 − t)
2
(3, 5) +
1
3
−2t
2
+30t − 110
(6, 2)
+
1
3
(t − 7)
2
(9, 4),
if 7 ≤ t ≤ 8.
(8.3)
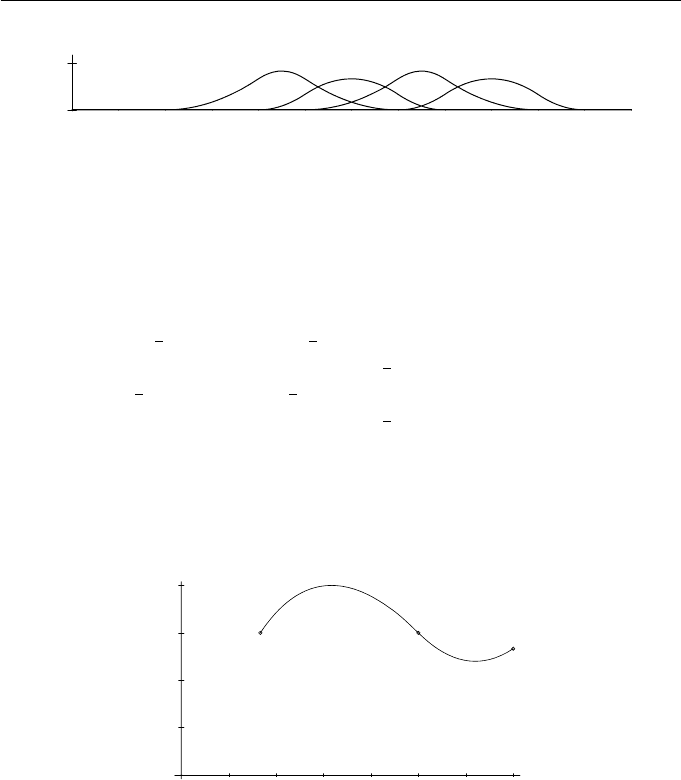
The B-spline curve, shown in Figure 8.3, is the union of two polynomial curve
segments.
0
1
2
3
4
1234
5
6
7
Figure 8.3 B-spline of Example 8.3
Whereas a B´ezier curve of degree d has exactly d + 1 control points, a B-
spline of degree d can have any number of control points provided a sufficient
number of knots are specified. Therefore, in order to define complex curve
shapes, B-splines can be given additional freedom by increasing the number of
control points, yet without increasing the degree of the curve.
Each basis function N
i,d
(t) is defined by d + 2 knots t
i
,...,t
i+d+1
.Soif
n + 1 control points are required, then it is necessary to specify n + d + 2 knots
t
0
,...,t
n+d+1
. Therefore, the number of knots equals the number of control

192 Applied Geometry for Computer Graphics and CAD
points plus the degree plus one, giving the identity
m = n + d +1.
A knot vector can have repeated knot values. The number of times a knot value
occurs is called the multiplicity of the knot. Define a new sequence u
0
,...,u
r
(u
0
< ···<u
r
), called the breakpoints, consisting of the distinct values of the
interior knots. Then the B-spline is the union of the polynomial curve segments
B
i
(t)ofdegreed, t ∈ [u
i
,u
i+1
).
Example 8.4
The breakpoints of Example 8.3 are u
0
=5,u
1
=7,andu
2
= 8, and the
B-spline consists of two segments. In Figure 8.3, the start and end points of
each segment are indicated by a • on the curve. The parametric equations of
the two polynomial curve segments are obtained from Equation (8.3)
B
0
(t)=
1
6
(7 − t)
2
(1, 2) +
1
3
−t
2
+12t − 34
(3, 5) +
1
6
(t − 5)
2
(6, 2)
=
−
65
3
+8t −
2
3
t
2
, −
701
18
+
133
9
t −
23
18
t
2
,
defined on [u
0
,u
1
)= [5, 7), and
B
1
(t)=
1
3
(8 − t)
2
(3, 5) +
1
3
−2t
2
+30t − 110
(6, 2) +
1
3
(t − 7)
2
(9, 4)
=
−
155
3
+
38
3
t −
2
3
t
2
, −
340
9
+
100
9
t −
7
9
t
2
,
defined on [u
1
,u
2
)=[7, 8].
Theorem 8.5
The B-spline basis functions N
i,k
(t) satisfy the following properties.
Positivity: N
i,k
(t) > 0fort ∈ (t
i
,t
i+k+1
).
Local Support: N
i,k
(t)=0fort/∈ (t
i
,t
i+k+1
).
Piecewise Polynomial: N
i,k
(t) are piecewise polynomial functions of
degree k.
Partition of Unity:
r
j=r−k
N
j,k
(t)=1,fort ∈ [t
r
,t
r+1
).
Continuity: If the interior knot t
i
has multiplicity p
i
,thenN
i,k
(t)isC
k−p
i
at t = t
i
. N
i,k
(t)isC
∞
elsewhere.
8. B-splines 193
Proof
The first three properties are proved by induction on k. The initial induction
step k = 0 is satisfied since it is clear from (8.1) that the basis functions N
i,0
(t)
satisfy the positivity and local support properties, and that they are piecewise
polynomial functions.
The induction hypothesis is that all basis functions of degree k, N
i,0
(t),...,
N
i,k
(t), satisfy the three properties. Then
N
i,k+1
(t)=
t − t
i
t
i+k+1
− t
i
N
i,k
(t)+
t
i+k+2
− t
t
i+k+2
− t
i+1
N
i+1,k
(t) ,
where N
i,k
(t) > 0fort ∈ (t
i
,t
i+k+1
), N
i,k
(t)=0fort/∈ (t
i
,t
i+k+1
),
N
i+1,k
(t) > 0fort ∈ (t
i+1
,t
i+k+2
), N
i+1,k
(t)=0fort/∈ (t
i+1
,t
i+k+2
).
Suppose t/∈ (t
i
,t
i+k+2
), then t/∈ (t
i
,t
i+k+1
), and t/∈ (t
i+1
,t
i+k+2
). Thus
N
i,k
(t)=0andN
i+1,k
(t) = 0, and hence N
i,k+1
(t) = 0 as required. Next,
suppose t ∈ (t
i
,t
i+k+2
). If t ∈ (t
i
,t
i+k+1
), then
t − t
i
t
i+k+1
− t
i
> 0,
t
i+k+2
− t
t
i+k+2
− t
i+1
> 0,N
i,k
(t) > 0,N
i+1,k
(t) ≥ 0 ,
which imply N
i,k+1
(t) > 0. Otherwise, t ∈ (t
i+1
,t
i+k+2
)and
t − t
i
t
i+k+1
− t
i
> 0,
t
i+k+2
− t
t
i+k+2
− t
i+1
> 0,N
i,k
(t) ≥ 0,N
i+1,k
(t) > 0 ,
which imply N
i,k+1
(t) > 0. In either case N
i,k+1
(t) > 0 as required.
Since the product of a polynomial and a piecewise polynomial is piecewise
polynomial, and the sum of two piecewise polynomials is piecewise polynomial,
it follows from (8.2), and the fact that N
i,k
(t)andN
i,k+1
(t) are piecewise
polynomial, that N
i,k+1
(t) is piecewise polynomial. Hence, by induction, the
first three properties are proved.
The partition of unity property is also proved by induction. The initial step
k = 0 is trivial. The induction hypothesis is that the partition of unity property
holds for the basis functions of degree k − 1. Then
r
j=r−k
N
j,k
(t)=N
r−k,k
(t)+···+ N
r−1,k
(t)+N
r,k
(t)
194 Applied Geometry for Computer Graphics and CAD
=
t−t
r−k
t
r
−t
r−k
N
r−k,k−1
(t)+
t
r+1
−t
t
r+1
−t
r−k+1
N
r−k+1,k−1
(t)
+
···+
t−t
r−1
t
r+k−1
−t
r−1
N
r−1,k−1
(t)+
t
r+k
−t
t
r+k
−t
r
N
r,k−1
(t)
+
t−t
r
t
r+k
−t
r
N
r,k−1
(t)+
t
r+k+1
−t
t
r+k+1
−t
r+1
N
r+1,k−1
(t)
=
t−t
r−k
t
r
−t
r−k
N
r−k,k−1
(t)+
t
r+1
−t
t
r+1
−t
r−k+1
+
t−t
r−k+1
t
r+1
−t
r−k+1
N
r−k+1,k−1
(t)+
···+
t
r+k
−t
t
r+k
−t
r
+
t−t
r
t
r+k
−t
r
N
r,k−1
(t)+
t
r+k+1
−t
t
r+k+1
−t
r+1
N
r+1,k−1
(t)
=
t−t
r−k
t
r
−t
r−k
N
r−k,k−1
(t)+N
r−k+1,k−1
(t)+
···+ N
r,k−1
(t)+
t
r+k+1
−t
t
r+k+1
−t
r+1
N
r+1,k−1
(t) .
Since N
r−k,k−1
(t)=0fort/∈ (t
r−k
,t
r
), and N
r+1,k−1
(t)=0fort/∈
(t
r+1
,t
r+k+1
), it follows that
r
j=r−k
N
j,k
(t)=N
r−k+1,k−1
(t)+···+ N
r,k−1
(t)=
r
j=r−k−1
N
j,k−1
(t) .
The induction hypothesis implies
r
j=r−k−1
N
j,k−1
(t)=1.
Hence
r
j=r−k
N
j,k
(t)=1,
and the partition of unit property is proved.
The property of continuity is proved in Lemma 8.15.
8.1.1 Properties of the B-spline Curve
A number of properties of B-spline curves are expressed in the following theo-
rem.
Theorem 8.6
A B-spline curve B(t)=
n
i=0
b
i
N
i,d
(t)ofdegreed defined on the knot vector
t
0
,...,t
m
satisfies the following properties.

8. B-splines 195
Local Control: Each segment is determined by d + 1 control points. If t ∈
[t
r
,t
r+1
)(d ≤ r ≤ m − d − 1), then
B(t)=
r
i=r−d
b
i
N
i,d
(t) .
Thus to evaluate B(t) it is sufficient to evaluate N
r−d,d
(t),...,N
r,d
(t).
Convex Hull:Ift ∈ [t
r
,t
r+1
)(d ≤ r ≤ m − d − 1), then
B(t) ∈ CH{b
r−d
, ..., b
r
} .
Continuity:Ifp
i
is the multiplicity of the breakpoint t = u
i
,thenB(t)is
C
d−p
i
(or greater) at t = u
i
,andC
∞
elsewhere.
Invariance under Affine Transformations: Let T be an affine transforma-
tion. Then T (
n
i=0
b
i
N
i,d
(t)) =
n
i=0
T (b
i
) N
i,d
(t).
Proof
Suppose t ∈ [t
r
,t
r+1
). Then the positivity property implies that N
i,d
(t)=0
for all i ≤ r − d − 1 and for all i ≥ r + 1. Hence B(t)=
n
i=0
b
i
N
i,d
(t)=
r
j=r−d
b
j
N
j,d
(t), and the local control property is proved.
Further, the partition of unity property gives
r
j=r−d
N
j,d
(t)=1. It fol-
lows from the definition of the convex hull (Section 6.6) and the local control
property that B(t) ∈ CH{b
r−d
, ..., b
r
} for all t, thus establishing the convex
hull property.
Since B(t) is piecewise polynomial, it is C
∞
everywhere except at the break-
points t = u
i
where the individual polynomial segments join. If u
i
is a break-
point of multiplicity p
i
,thenN
i,d
(t)isC
d−p
i
at t = u
i
and C
∞
elsewhere.
Hence, at t = u
i
, B(t) is a sum of functions which are either C
d−p
i
or C
∞
.
Hence B(t) has continuity C
d−p
i
.
Invariance under affine transformations is proved in a similar manner to the
corresponding result for B´ezier curves.

196 Applied Geometry for Computer Graphics and CAD
8.1.2 B-spline Types
Open B-splines
In general, B-spline curves do not interpolate the first and last control points
b
0
and b
n
. For curves of degree d, endpoint interpolation and an endpoint
tangent condition are obtained by open B-splines for which the end knots satisfy
t
0
= t
1
= ... = t
d
and t
m−d
= t
m−d+1
= ... = t
m
. A minor modification of the
definition of the basis functions (8.1) is required in order to accommodate the
multiplicity of the knots: N
m−d−1
should take the value 1 at t = m −d (and 0
elsewhere). Since t
d
∈ [t
d
,t
d+1
), the local control property with r = d gives
B(t
d
)=
d
j=0
b
j
N
j,d
(t
d
) .
For 0 ≤ j ≤ d,
N
j,d
(t
d
)=
t
d
−t
j
t
j+d
−t
j
N
j,d−1
(t
d
)+
t
j+1+d
−t
d
t
j+1+d
−t
j+1
N
j+1,d−1
(t
d
) .
Since t
0
= t
1
= ... = t
d
,thent
j
= t
d
, and therefore (applying the convention
0/0 = 0 for the case j =0)
N
j,d
(t
d
)=(0)N
j,d−1
(t
d
)+
t
j+1+d
−t
d
t
j+1+d
−t
j+1
N
j+1,d−1
(t
d
) .
Therefore
N
j,d
(t
d
)=
t
j+1+d
−t
d
t
j+1+d
−t
j+1
t
d
−t
j+1
t
j+d
−t
j+1
N
j+1,d−2
(t
d
)+
t
j+2+d
−t
d
t
j+2+d
−t
j+2
N
j+2,d−2
(t
d
)
.
Repeated similar simplifications and replacements of basis functions by ones of
lower order yields
N
j,d
(t
d
)=
t
j+1+d
−t
d
t
j+1+d
−t
j+1
t
j+2+d
−t
d
t
j+2+d
−t
j+2
...
t
d+j+d
−t
d
t
d+j+d
−t
j+d
N
j+d,0
(t
d
) . (8.4)
Since N
j+d,0
(t
d
)=0forj>0, it follows from (8.4) that N
j,d
(t
d
)=0forj>0.
When j = 0, identities (8.4) and N
d,0
(t
d
) = 1 give
N
0,d
(t
d
)=
t
1+d
−t
d
t
1+d
−t
1
t
2+d
−t
d
t
2+d
−t
2
...
t
d+d
−t
d
t
d+d
−t
d
N
d,0
(t
d
)=1.
Hence
B(t
d
)=
d
j=0
b
j
N
j,d
(t
d
)=b
0
.
Similarly,
B(t
m−d
)=b
n
.
