Marsh D. Applied Geometry for Computer Graphics and CAD

Подождите немного. Документ загружается.

7. B´ezier Curves II 167

Example 7.7

The curve (2 + 5t − 3t

, 4 − t +6t

) is converted into quadratic B´ezier form as

follows

⎛

⎝

100

111

⎞

⎠

⎛

⎝

5 −1

−36

⎞

⎠

⎛

⎝

2.04.0

4.53.5

4.09.0

⎞

⎠

Hence the control points of the quadratic B´ezier curve are

(2.0, 4.0), b

(4.5, 3.5), and b

(4.0, 9.0) .

EXERCISES

7.7. Convert the curve (1 − t

, 4 − 2t +3t

)intoB´ezier form.

7.8. Convert the quadratic B´ezier curve with control points

(−3.0, −3.0), b

(1.0, −1.0), and b

(−1.0, 2.0) into monomial form.

7.9. Let B =



0,2

(t) B

1,2

(t) B

2,2

(t)



and T =



1 tt



. Show

that

B = T·Bez, and B(t)=T·Bez·b . (7.8)

The procedure for conversion between the general B´ezier curve and a curve

in monomial form is similar. Let

B =



0,n

(t) B

1,n

(t) ... B

n,n

(t)



, T =



1 t ... t



a =



... a



, b =



... b



and let the matrices Bez =(Bez

i,j

)andBez

−1



Bez

−1

i,j



, 0 ≤ i, j ≤ n, have

entries respectively deﬁned by

Bez

i,j



(−1)

i−j







, if i ≥ j

0, otherwise

, and

Bez

−1

i,j













, if j ≤ i

0, otherwise

Then identities (7.7) and (7.8) hold. The most eﬃcient computer implementa-

tion for conversion between a

and b

is yielded by the equivalent formulae



j=0

(−1)

i−j









j=0







168 Applied Geometry for Computer Graphics and CAD

EXERCISES

7.10. Following the approach taken for conversions of quadratic polyno-

mial curves, show that for cubic curves

Bez =

⎛

⎜

⎝

1000

−3300

3 −630

−13−31

⎞

⎟

⎠

7.11. Show that the matrix

Bez

−1

=1/3

⎛

⎜

⎝

3000

3100

3210

3333

⎞

⎟

⎠

is the inverse of the matrix Bez given in Exercise 7.10.

7.12. Convert the curve (2 −3t −4t

+7t

, −4+8t −5t

)intoB´ezier form.

7.13. Convert the B´ezier curve with control points b

(2, −1), b

(5, 2),

(7, 3), and b

(6, −1) into monomial form.

7.4 Piecewise B´ezier Curves

AB´ezier curve of degree n has n + 1 control points. Curves of high degree

are not often used since there is only a weak relationship between the shape

of the curve and the shape of the control polygon. Further, operations such

as the evaluation of points require a large number of arithmetical operations,

and so there is an increased risk of computational errors. In contrast, curves

of low degree have few control points, and therefore yield a limited range of

curve shapes. To widen the range of shapes without increasing the degree of

the curve, a number of B´ezier curves can be joined end to end to form a single

continuous curve called a piecewise B´ezier curve. In practice, the joins of the

curves are required to be smooth.

Deﬁnition 7.8

An arbitrary interval B´ezier curve B(t)ofdegreen with control points

7. B´ezier Curves II 169

,...,b

deﬁnedonaninterval[t

min

max

]isgivenby

B(t)=



i=0

i,n



t − t

min

max

− t

min



where B

i,n

denote the Bernstein basis functions of degree n. The arbitrary

interval B´ezier curve B(t) is a reparametrization of the ordinary B´ezier curve

B(t)=



i=0

i,n

(t), t ∈ [0, 1].

B(t) is said to be the normalization of B(t).

Deﬁnition 7.9

Let I =[a, b]. P(t)issaidtobeapiecewise B´ezier curve if there exist t

< ···<t

r−1

such that a = t

and b = t

, and arbitrary interval B´ezier

curves B

(t)deﬁnedon[t

j+1

](j =0,...,r− 1), such that (i) P(t)=B

(t)

for t ∈ (t

j+1

), (ii) P(t

)=B

j−1

)orP(t

)=B

) (possibly both) for

j =1,...,r−1, and (iii) P(t

)=B

)andP(t

)=B

r−1

). The parameter

values t

are called breakpoints. If the largest degree of the curves B

(t)isn,

then the piecewise B´ezier curve is said to have degree n. The terms quadratic,

cubic, etc. are used to describe piecewise curves of degrees two, three, etc.

Remark 7.10

The deﬁnition ensures that P(t) is single valued on the interval [a, b]. In prac-

tice, a piecewise B´ezier curve is considered simply as a union of B´ezier curves

and therefore P(t

)hastwo values (j =1,...,r − 1), namely B

j−1

)and

). In many applications only continuous curves are considered, in which

case P(t

)=B

j−1

)=B

)andsoP(t) is single valued everywhere.

Example 7.11

Consider three arbitrary interval B´ezier curves B

(t), t ∈ [−2, 0]; B

(t), t ∈

[0, 3]; B

(t), t ∈ [3, 4] with the following control points

(t):b

(2, −1), b

(5, 2), b

(7, 3), b

(8, −1)

(t):b

(8, −1), b

(8, −3), b

(7, −4), b

(5, −4)

(t):b

(5, −4), b

(3, −4), b

(4, −2), b

(6, −2) .

Let P(t) be the piecewise B´ezier curve deﬁned on the interval [−2, 4] given by

P(t)=

⎧

⎨

⎩

(t) , −2 ≤ t<0

(t) , 0 ≤ t<3

(t) , 3 ≤ t ≤ 4

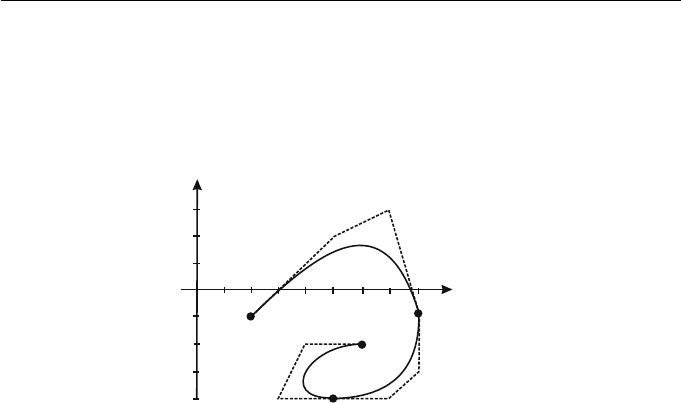
170 Applied Geometry for Computer Graphics and CAD

The breakpoints are t

= −2, t

=0,t

=3,t

= 4. Since the parametrization

does not aﬀect the trace of a curve, P(t) can be plotted by drawing the nor-

malizations of B

(t) which are the B´ezier curves deﬁned by the same sets of

control points. The curve is shown in Figure 7.1.

-3

-2

-1

5 6 7 8

-4

Figure 7.1

Recall that a parametric curve C(t)issaidtobeC

-continuous whenever all

of the coordinate functions are C

-continuous. Since a polynomial function is

∞

, a piecewise polynomial function is C

∞

everywhere except at the parameter

values corresponding to the joins of the individual functions. It can be shown

that, at the join of two polynomial functions of degrees p and q, the piecewise

function is at most C

-continuous where k = min(p, q). It follows that at the

join of two polynomial curves of degrees p and q, the piecewise curve is at most

-continuous where k = min(p, q).

Example 7.12

Consider the curve (x(t),y(t)) = (t, f(t)) where

f(t)=



+2t +1, if t ≤ 0

t +1, if t>0

The curve is shown in Figure 7.2(a). Since any polynomial function is C

∞

x(t)=t is C

∞

everywhere, and y(t)=f(t)isC

∞

everywhere except possibly

at t = 0, the parameter value at which the second polynomial function takes

over from the ﬁrst in the deﬁnition of f . It is easily checked that f(t)isC

.To

determine whether f(t)isC

it is necessary to consider its ﬁrst derivative



(t)=



6t +2, if t ≤ 0

1, if t>0

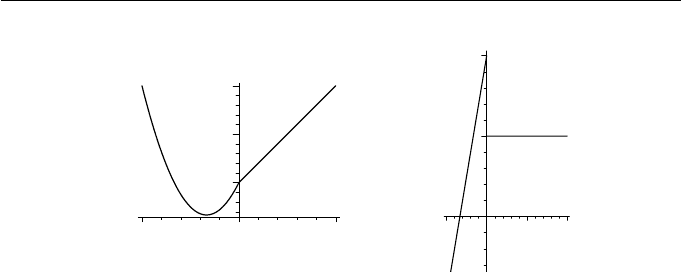
7. B´ezier Curves II 171

1.5

–1 0 1

–0.5 0.5

Figure 7.2 (a) Graph of (t, f(t)) (b) Graph of f



(t)

The graph of f



(t) is shown in Figure 7.2(b). It is clear that f is not C

geometrically, the graph of f



(t) has a break at t = 0. Hence (t, f(t)) is a

-continuous curve, but not C

The piecewise curve in this example is the join of the two polynomial curves

(t, 3t

+2t+1) and (t, t+ 1). Since k = min(2, 1) = 1 for curves of degrees p =2

and q = 1, the maximum continuity possible is C

; the example only achieves

-continuity.

Suppose P(t) is a piecewise B´ezier curve deﬁned on I =[a, b], consisting

of B´ezier curves B

(t) deﬁned on intervals I

=[t

j+1

](j =0,...,r− 1) as

expressed in Deﬁnition 7.9. Since the coordinate functions of P(t) are piece-

wise polynomial functions, P(t)isC

∞

at all parameter values which are not

breakpoints. Suppose B

(t) has degree n

and control points b

,...,b

.Then

P(t) is continuous at t = t

if and only if lim

t→t

P(t) = lim

t→t

−

P(t)=P(t

(This is a standard criterion for continuous functions, see [25].) But

lim

t→t

P(t) = lim

t→t

(t)=b

, and

lim

t→t

−

P(t) = lim

t→t

−

j−1

(t)=b

j−1

Thus P(t) is continuous at t = t

if and only if P(t

)=b

j−1

= b

. Hence

the last control point of B

j−1

(t) should equal the ﬁrst control point of B

(t).

Therefore P(t) is continuous if and only if b

j−1

= b

for all j =1,...,r− 1.

Example 7.13

Consider the piecewise cubic B´ezier curve consisting of two cubic B´ezier curves

B(t)andC(t) with control points b

, b

and c

, c

respectively.

172 Applied Geometry for Computer Graphics and CAD

Assuming that B(t) is the ﬁrst curve and C(t) is the second, the piecewise

cubic B´ezier curve is C

if and only if b

= c

Let P

(p)

denote the pth derivative of P(t). Then

lim

t→t

(p)

(t) = lim

t→t

(p)

(t) ,

lim

t→t

−

(p)

(t) = lim

t→t

−

(p)

j−1

(t) .

Thus B(t)isC

if and only if for all p ≤ k and for all j =1,...,r− 1,

(p)

j−1

)=B

(p)

) . (7.9)

The condition (7.9) for C

-continuity can be expressed in terms of the normal-

ized B´ezier curves. Since B

(t)=

(

t−t

min

max

−t

min

) the chain rule yields

− t

j−1

)

(p)

j−1

(1) =

j+1

− t

)

(p)

(0) . (7.10)

This is a more useful formula since the derivatives of

(p)

are easily obtained

in terms of the control points using Theorem 7.3 and its corollaries.

Deﬁnition 7.14

Suppose two regular curves B(s), s ∈ [s

], and C(t), t ∈ [t

], meet at

apointP = B(s

)=C(t

). Then the two curves are said to meet with G

continuity whenever there is a reparametrization α :[u

] → [s

]such

that s

= α(u

)and

(α(u))



u=u

(t)



t=t

for all i =0,...,k. This type of continuity is called geometric continuity.(The

notation |

t=t

indicates that the function is evaluated at t

If two curves meet with G

-continuity at a point P, then their tangent

vectors at P have the same direction, but they may have diﬀerent magnitudes.

To the eye, the curves meet smoothly and the curves are said to be visually

tangent continuous at P. It is left as an exercise to the reader to show that

B(s)andC(t)areG

-continuous at P if and only if

) (7.11)

7. B´ezier Curves II 173

for some µ = 0 (using the notation of Deﬁnition 7.14), and that C

-continuity

is obtained whenever (7.11) is satisﬁed for µ =1.

Suppose P(t) is a continuous piecewise B´ezier curve. Then P(t) is visually

tangent continuous at t = t

whenever there exist constants µ

> 0, such that



j−1

)=B



). When the piecewise B´ezier curve is given by B´ezier

curves B

(t) deﬁned on intervals of unit length (that is t

− t

j−1

= 1 for all

j) condition (7.10) simpliﬁes to

(p)

j−1

(1) =

(p)

(0). Then Theorem 7.3 yields

the conditions for C

-continuity and visual tangent continuity in terms of the

control points alone. So, in eﬀect the intervals can be ignored and it is common

practice to work as if ordinary B´ezier curves are being used to construct the

piecewise curve. Examples are given below.

Example 7.15

Consider a piecewise B´ezier curve consisting of two cubic B´ezier curves B(t)and

C(t) (deﬁned on intervals of unit length) with control points b

, b

,and

, c

, respectively. Suppose that b

= c

so that the piecewise curve is

continuous. Visual tangent continuity is obtained when µB



(1) = C



(0). Then



(1) = 3(b

− b

)andC



(0) = 3(c

− c

), giving µ3(b

− b

)=3(c

− c

Substituting c

= b

and simplifying gives c

=(1+µ) b

− µb

. Hence b

,andc

are collinear, and b

lies between b

and c

. Geometrically, the

visual tangent continuity implies that the tangent direction at the end of the

ﬁrst segment equals the tangent direction at the beginning of the second seg-

ment. The resulting join of the two curves appears smooth, but the underlying

parametrization is not C

-continuous. C

-continuity is achieved when µ =1,

so that the magnitudes and directions of the tangents are equal. Hence c

= b

and c

=2b

− b

. The arguments above are easily generalized to give conti-

nuity conditions for B´ezier curves of degree n expressed in Theorem 7.17.

Example 7.16

Consider the piecewise curve consisting of two cubic B´ezier curves (deﬁned on

intervals of unit length) with control points b

(2, 5), b

(3, 1), b

(5, 1), b

(6, 3),

and c

(6, 3), c

(8, 7), c

(5, 8), c

(3, 6). Since b

= c

=(6, 3), the two curves

join to form a continuous curve. Further, the condition c

=(1+µ) b

− µb

gives

(8, 7) = (1 + µ)(6, 3) − µ(5, 1)

which is satisﬁed for µ =2> 0, and hence the curve is visually tangent

continuous. C

-continuity can be obtained by adjusting a control point. For

instance, if c

is changed to (7, 5), then c

=2b

− b

is satisﬁed.

174 Applied Geometry for Computer Graphics and CAD

Theorem 7.17

Two B´ezier curves of degree n,

B(t)=



i=0

i,n

(t), and C(t)=



i=0

i,n

(t),

deﬁned on intervals of unit length, join to form a piecewise curve with

1. C

-continuity if and only if b

= c

(or c

= b

);

2. C

-continuity if and only if b

= c

and c

=2b

−b

n−1

(or c

= b

and

=2c

− c

n−1

);

3. visual tangent continuity if and only if b

= c

,and

=(1+µ) b

− µb

n−1

for some µ (or c

= b

and b

=(1+µ) c

− µc

n−1

Corollary 7.18

Using the earlier notation, a piecewise B´ezier curve B(t) for which the B´ezier

curves B

(t) are deﬁned on unit length intervals has

1. C

-continuity if and only if b

= b

i+1

for i =1,...,r− 1;

2. C

-continuity if and only if b

= b

i+1

and b

i+1

=2b

− b

n−1

for i =

1,...,r− 1;

3. visual tangent continuity if and only if b

= b

i+1

and b

i+1

=(1+µ

) b

−

n−1

,forsomeµ

,fori =1,...,r− 1.

EXERCISES

7.14. Consider the piecewise curve consisting of two cubic B´ezier curves

with control points b

(2, 1), b

(4, 2), b

(5, 4), b

(3, 6), and c

(3, 6),

(2, 7), c

(0, 5), c

(0, 3). Show that the curves have visual tangent

continuity. Plot the curves and their control polygons. Alter the con-

trol point b

so that the curves join with C

-continuity.

7.15. Determine the conditions on the control points for C

-,C

-, and

-continuity of two quadratic B´ezier curves (deﬁned on intervals of

unit length).

7.16. Determine the conditions on the control points for C

-continuity of

two cubic B´ezier curves (deﬁned on unit intervals). Determine the

conditions for C

-continuity of two B´ezier curves of degree n.

7. B´ezier Curves II 175

7.5 Rational B´ezier Curves

In Section 5.6.1 it was shown that there are three types of irreducible conics,

namely, hyperbolas, parabolas, and ellipses. Parabolas can be parametrized

by polynomial functions, whereas hyperbolas and ellipses are parametrized

by rational functions. Thus quadratic B´ezier curves, which have polynomial

parametrizations, exclude hyperbolas and ellipses. In order to represent such

curves it is necessary to introduce rational B´ezier curves.

Deﬁnition 7.19

A rational B´ezier curve of degree n with control points b

,...,b

and corre-

sponding scalar weights w

is deﬁned to be

B(t)=



i=0

i,n

(t)



i=0

i,n

(t)

,t∈ [0, 1] ,

with the understanding that if w

=0,thenw

is to be replaced by b

.Itis

assumed that not all the weights are zero. When b

∈ R

(i =0,...,n)then

the curve is planar, and when b

∈ R

the curve is spatial. Note that the term

integral B´ezier curve is used to describe non-rational B´ezier curves.

Let b

=(x

). Deﬁne homogeneous control points



), if w

=0

, 0), if w

In homogeneous coordinates the rational B´ezier curve is given by

B(t)=



i=0

i,n

(t)

which takes the form of an integral B´ezier curve, but with homogeneous control

points. Since



i=0

i,n

(t) = 1, by the partition of unity property, integral

B´ezier curves are obtained whenever w

= ···= w

A rational B´ezier curve can also be written in the basis form

B(t)=



i=0

i,n

(t)

where

i,n

(t)=

⎧

⎨

⎩

i,n

(t)



j=0

j,n

(t)

, if w

=0

i,n

(t)



j=0

j,n

(t)

, if w

176 Applied Geometry for Computer Graphics and CAD

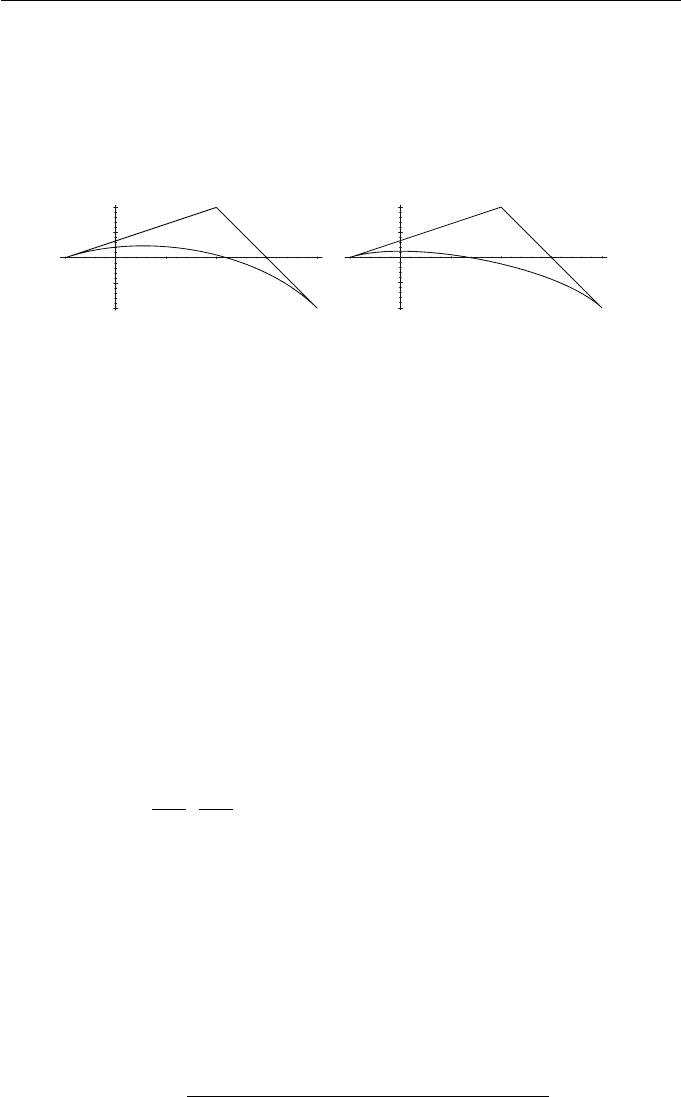
Example 7.20

The rational quadratic with control points b

(−1, 0), b

(2, 1), and b

(4, −1)

and corresponding weights 1, 1, 2 is shown in Figure 7.3(a), and with weights

1, 0.6, 2 is shown in Figure 7.3(b).

-1

-0.5

0.5

-1 1 2 3 4

-1

-0.5

0.5

11234

(a) (b)

Figure 7.3 Rational B´ezier curve with control points (−1, 0), (2, 1),

(4, −1), and (a) weights 1, 1, 2, and (b) weights 1, 0.6, 2

Example 7.21

The unit quarter circle in the ﬁrst quadrant can be represented as a quadratic

rational B´ezier curve with control points b

(1, 0), b

(1, 1), and b

(0, 1) and

weights w

=1,w

=1,andw

=2.Then

(1 − t)

+2t(1 − t)w

+ t

=(1− t)

(1, 0) + 2t(1 − t)(1, 1) + 2t

(0, 1)



1 − t

, 2t



(1 − t)

+2t(1 − t)w

+ t

=(1− t)

+2t(1 − t)+2t

=1+t

Hence B(t)=



1−t

1+t



which is a familiar parametrization of the unit

quarter circle.

Example 7.22

The spatial rational cubic B´ezier curve with control points b

(1, 0, 1),

(2, 1, −1), b

(5, 4, 2), and b

(2, −3, 1) and weights 1, 2, 2, 1 is shown in Fig-

ure 7.4.

A quadratic rational B´ezier curve has the form

B(t)=

0,2

(t)+w

1,2

(t)+w

2,2

(t)

0,2

(t)+w

1,2

(t)+w

2,2

(t)

. (7.12)