Marsh D. Applied Geometry for Computer Graphics and CAD

Подождите немного. Документ загружается.

6. B´ezier Curves I 147

6.7 Properties of B´ezier Curves

Theorem 6.8

AB´ezier curve B(t)ofdegreen with control points b

, ..., b

satisﬁes the

following properties.

Endpoint Interpolation Property: B(0) = b

and B(1) = b

Endpoint Tangent Property:



(0) = n (b

− b

)andB



(1) = n (b

− b

n−1

) .

Convex Hull Property (CHP): For all t ∈ [0, 1], B(t) ∈ CH{b

, ..., b

Thus every point of a B´ezier curve lies inside the convex hull of its deﬁning

control points. The convex hull of the control points is often referred to as

theconvexhulloftheB´ezier curve.

Invariance under Aﬃne Transformations: Let T be an (aﬃne) transfor-

mation (for example, a rotation, reﬂection, translation, or scaling). Then





i=0

i,n

(t)





i=0

T (b

) B

i,n

(t) .

Variation Diminishing Property (VDP): For a planar B´ezier curve B(t),

the VDP states that the number of intersections of a given line with B(t)

is less than or equal to the number of intersections of that line with the

control polygon.

Proof

The proof of the endpoint interpolation property is Exercise 6.23. The endpoint

tangent property follows from Theorem 7.3 which will be proved later.

(Convex Hull Property) From the deﬁnition of the convex hull expressed in

Equation (6.5) it is suﬃcient to show that every point B(t)onaB´ezier curve

has the form a

+ ···+ a

for some constants a

satisfying



i=0

=1.

Let a

= B

i,n

(t), then positivity implies a

≥ 0, the partition of unity implies

that



i=0

= 1, and the proof is complete. Figure 6.9 illustrates the CHP for

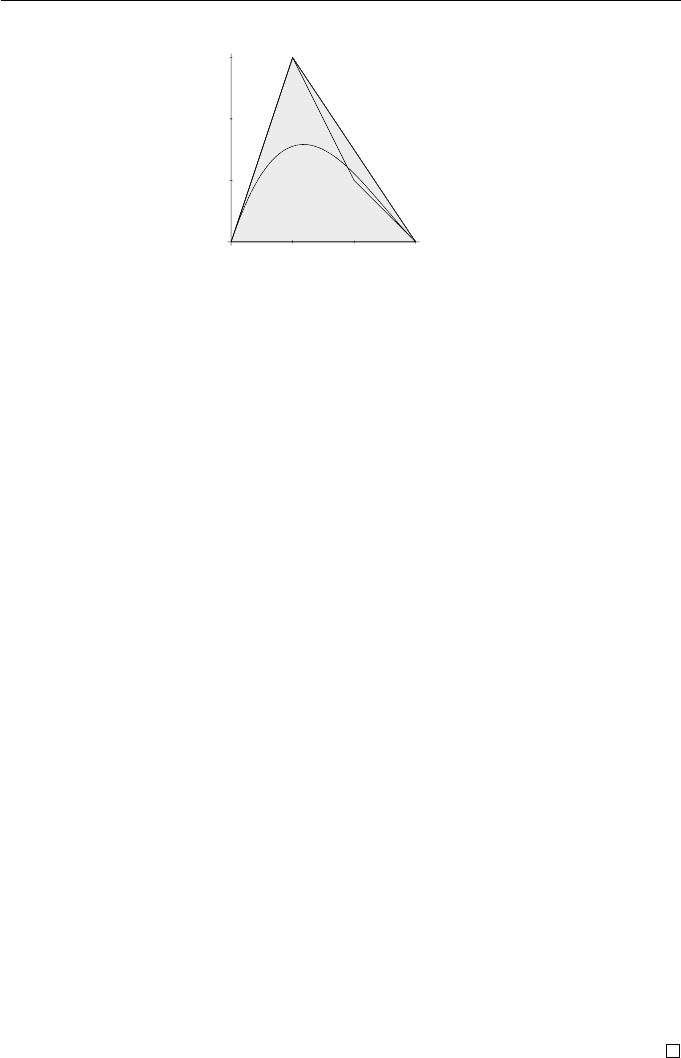
a cubic B´ezier curve.

(Aﬃne Invariance) Let an aﬃne transformation T be given by



)=(ax + by + c, dx + ey + f) ,

148 Applied Geometry for Computer Graphics and CAD

01 2 3

Figure 6.9 Convex hull property for a cubic B´ezier curve

and let a B´ezier curve of degree n have control points b

)fori =0,...,n.

Then

B(t)=(x(t),y(t)) =





i=0

i,n

(t),



i=0

i,n

(t)



Applying the transformation yields

T(B(t)) =





i=0

i,n

(t)+b



i=0

i,n

(t)+c,



i=0

i,n

(t)+e



i=0

i,n

(t)+f



Then, by partition of unity,



i=0

i,n

(t) = 1, and

T(B(t)) =





i=0

i,n

(t)+b



i=0

i,n

(t)+c



i=0

i,n

(t),



i=0

i,n

(t)+e



i=0

i,n

(t)+f



i=0

i,n

(t)







i=0

(ap

+ bq

+ c)B

i,n

(t),



i=0

(dp

+ eq

+ f)B

i,n

(t)





i=0

(ap

+ bq

+ c, dp

+ eq

+ f)B

i,n

(t)



i=0

T(b

i,n

(t) .

6. B´ezier Curves I 149

Example 6.9

Consider a cubic B´ezier curve with vertices b

(1, 0), b

(2, 3), b

(5, 4), and

(2, 1). To apply a rotation through an angle π/4 about the origin in the

anticlockwise direction to the curve, it is suﬃcient to apply the rotation matrix

Rot(π/4) to the homogeneous coordinates of the control points:

⎛

⎜

⎝

101

231

541

211

⎞

⎟

⎠

⎛

⎝

cos π/4sinπ/40

−sin π/4cosπ/40

001

⎞

⎠

⎛

⎜

⎝

0.707 0.707 1.0

−0.707 3.536 1.0

0.707 6.364 1.0

0.707 2.121 1.0

⎞

⎟

⎠

The control points of the rotated curve are b

(0.707, 0.707), b

(−0.707, 3.536),

(0.707, 6.364), and b

(0.707, 2.121). The curve and its rotated image are

illustrated in Figure 6.10.

1234

Figure 6.10 Application of a rotation to a cubic B´ezier curve

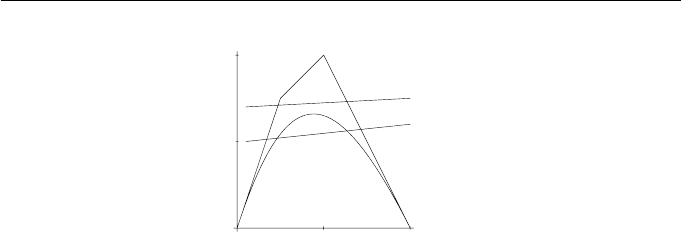
Figure 6.11 illustrates two lines intersecting a B´ezier curve and its control

polygon. The upper line intersects the polygon in two points but does not

intersect the curve. The lower line intersects both the polygon and the curve

in two points. In both cases, the number of intersections with the given line is

equal to or greater than the number of intersections of the line with the curve.

Thus the variation diminishing property is satisﬁed. The proof of the variation

diminishing property is beyond the scope of this book, and the reader is referred

to [15].

150 Applied Geometry for Computer Graphics and CAD

01 2

Figure 6.11 Variation diminishing property

EXERCISES

6.22. Plot the cubic B´ezier curve deﬁned by control points b

(0, 1),

(2, 5), b

(4, 6), and b

(8, 1). On the same plot, draw the control

polygon. Observe that the resulting curve satisﬁes the convex hull

property. Next plot the B´ezier cubic with control points b

(1, 1),

(3.4, 1.8), b

(6, 6.5), and b

(9, 1). Does the newly displayed curve

violate the convex hull property? Explain.

6.23. Prove the endpoint interpolation property for the general B´ezier

curve: B(0) = b

and B(1) = b

6.24. Prove that when the control points are collinear, the resulting B´ezier

curve is a straight line segment.

6.25. Determine the control points of the image of the B´ezier curve with

control points b

(0, 0), b

(2, 1), b

(3, −1), and b

(1, −2) when the

following transformations have been applied

(a) a translation of 3 units in the x-direction and 4 units in the

y-direction,

(b) a rotation about the origin through an angle of π/2 radians in

an anti-clockwise direction,

For each transformation plot the image curve and its control polygon.

6.26. The basis functions B

0,3

(t)=(1−t)

, B

1,3

(t)=2t(1−t)

, B

2,3

(t)=

(1 − t), B

0,3

(t)=t

give rise to a representation for cubic curves

B(t)=



i=0

i,3

(t).

(a) Show that if b

= b

then B(t) is a quadratic curve with control

polygon b

, b

and b

6. B´ezier Curves I 151

(b) Show that the representation satisﬁes end interpolation and

tangent properties similar to B´ezier curves.

6.8 The de Casteljau Algorithm

The de Casteljau algorithm provides a method for evaluating the point on a

B´ezier curve corresponding to the parameter value t ∈ [0, 1]. In Section 6.9 it

will be shown that the same algorithm can be used to divide a curve into two

curve segments. For the case of a cubic B´ezier curve with control points b

,andb

, and for a speciﬁed parameter value t ∈ [0, 1], the de Casteljau

algorithm is expressed by the recursive formula



= b

=(1− t)b

j−1

+ tb

j−1

i+1

for j =1, 2, 3andi =0,...,3 − j. The formula generates a triangular set of

values (6.6) for which b

= B(t) for the speciﬁed value of t:

(6.6)

Example 6.10

A cubic B´ezier curve has control points b

(1.0, 1.0), b

(2.0, 7.0), b

(8.0, 6.0),

and b

(12.0, 2.0). The point B(0.25) is determined by applying the de Casteljau

algorithm with t =0.25. Then

(1.0, 1.0) +

(2.0, 7.0) = (1.25, 2.5),

(2.0, 7.0) +

(8.0, 6.0) = (3.5, 6.75),

(8.0, 6.0) +

(12.0, 2.0) = (9.0, 5.0),

(1.25, 2.5) +

(3.5, 6.75) = (1.8125, 3.5625), etc.

152 Applied Geometry for Computer Graphics and CAD

The algorithm gives the following table of points:

(1.0, 1.0) (2.0, 7.0) (8.0, 6.0) (12.0, 2.0)

↓

(1.25, 2.5) (3.5, 6.75) (9.0, 5.0)

↓

(1.8125, 3.5625) (4.875, 6.3125)

↓

(2.578, 4.25)

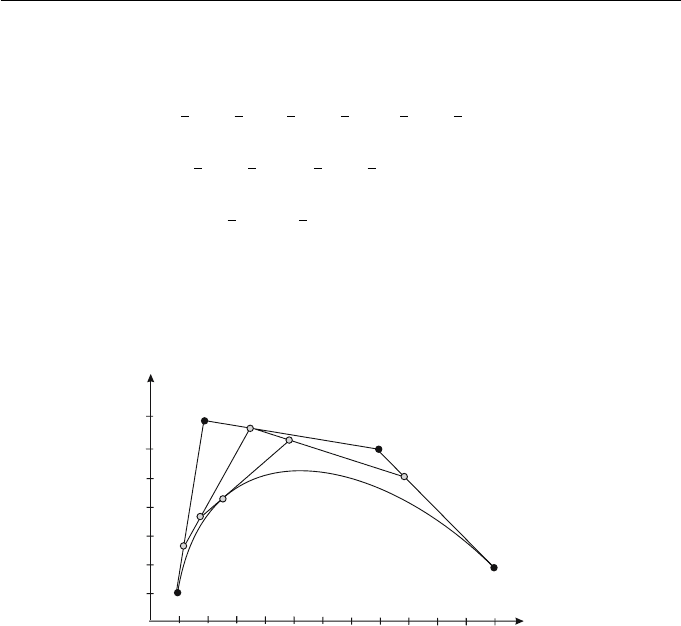
The algorithm yields B(0.25) = (2.578, 4.25). Geometrically, each step of the

algorithm is a linear interpolation of the control polygon as illustrated in Fig-

ure 6.12.

0 1 2 3 4 5 6

7 8 9 10 11 12

Figure 6.12 The de Casteljau algorithm with t =0.25

Theorem 6.11

Let a B´ezier curve of degree n be given by control points b

,...,b

, and let

t ∈ [0, 1] be any parameter value. Then B(t)=b

,whereb

= b

,and

= b

j−1

(1 − t)+b

j−1

i+1

for j =1,...,n,andi =0,...,n− j.

Proof

The de Casteljau algorithm follows from the recursion property of the Bernstein

polynomials

i,n

(t)=(1− t)B

i,n−1

(t)+tB

i−1,n−1

(t) . (6.7)

6. B´ezier Curves I 153

Then

B(t)=



i=0

i,n

(t)=



i=0

((1 − t)B

i,n−1

(t)+tB

i−1,n−1

(t))



i=0

(1 − t)B

i,n−1

(t)+



i=0

i−1,n−1

(t) .

Since B

n,n−1

(t) = 0, and B

−1,n−1

(t) = 0 it follows that

B(t)=

n−1



i=0

(1 − t)B

i,n−1

(t)+



i=1

i−1,n−1

(t) .

Next renumber the second summation by replacing i by i +1,

B(t)=

n−1



i=0

(1 − t)B

i,n−1

(t)+

n−1



i=0

i+1

i,n−1

(t)

n−1



i=0

(1 − t)+b

i+1

t) B

i,n−1

(t) .

Set b

= b

(1 − t)+b

i+1

t = b

(1 − t)+b

i+1

t for i =0,...,n− 1, then

B(t)=

n−1



i=0

i,n−1

(t) . (6.8)

Equation (6.8) expresses B(t)asaB´ezier curve of degree n − 1 with control

points b

,...,b

n−1

. Applying a similar argument yields

B(t)=

n−2



i=0

i,n−2

(t) ,

where b

i+1

= b

(1 − t)+b

i+1

t for i =0,...,n− 2. In general,

B(t)=

n−j



i=0

i,n−j

(t) ,

where b

= b

j−1

(1 − t)+b

j−1

i+1

t for i =0,...,n− j. In particular, j = n gives

B(t)=



i=0

i,n−n

(t)=b

154 Applied Geometry for Computer Graphics and CAD

EXERCISES

6.27. A cubic B´ezier curve has control points b

(1, 0), b

(3, 3), b

(5, 5),

and b

(7, 2). Evaluate the point B(0.25) by (a) applying the de Cast-

eljau algorithm, and (b) substituting t =0.25 into the deﬁning equa-

tion of the B´ezier curve. Make a sketch illustrating the points derived

in applying de Casteljau algorithm.

6.28. Apply the de Casteljau algorithm to the quartic B´ezier curve with

control points b

(3.0, 3.0), b

(4.0, 2.0), b

(−1.0, 0.0), b

(6.0, 1.0),

and b

(8.0, 5.0), and evaluate the point B(0.6).

6.29. (Used in Theorem 6.13) Prove that the intermediate control points

deﬁned in the de Casteljau algorithm satisfy



i=0

i,j

(t)b

i+k

6.30. Show that

(1 − t)B

(t)=



n +1− i

n +1



n+1

(t) ,

(t)=



i +1

n +1



n+1

i+1

(t) .

6.31. (Used in Theorem 6.13) Use Exercise 6.29 (or otherwise) to show

that B

i,n

(αt)=



j=0

i,j

(α)B

j,n

(t).

6.9 Subdivision of a B´ezier Curve

AB´ezier curve is generally deﬁned over the interval [0, 1] and given by

B(t)=



i=0

i,n

(t). On occasions, only a part of a curve is of interest.

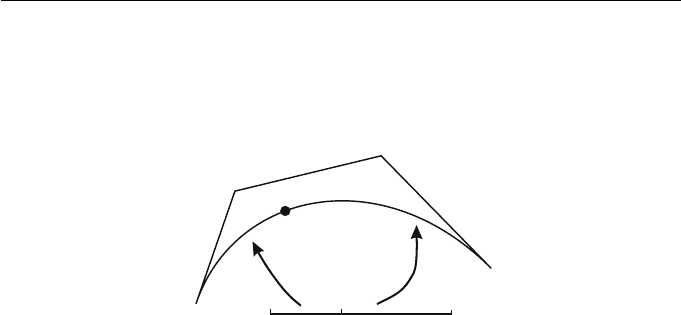
For instance, suppose that a B´ezier curve is “cut” at the parameter value t = α

to give two curve segments, denoted by B

left

(t)andB

right

(t), deﬁned over the

intervals [0,α], and [α, 1] as shown in Figure 6.13. Since B

left

(t)andB

right

(t)

are polynomial curves they can be represented in B´ezier form over the interval

[0, 1]. Theorem 6.13 will show that to determine the control points of B

left

(t)

and B

right

(t) it is suﬃcient to apply the de Casteljau algorithm to B(t) with

t = α. For a cubic B´ezier curve, the theorem implies that the control points of

left

(t)areb

, b

, and the control points of B

right

(t)areb

, b

The two sets of points are observed to be two edges of the triangle of control

6. B´ezier Curves I 155

points (6.6). Subdivision is one way of creating extra control points in order

to give additional freedom for curve design. For instance, one segment of the

curve can be left untouched while the other part of the curve is changed.

0 1

left

right

B()a

Figure 6.13

Example 6.12

AB´ezier cubic B(t) has control points b

(1.0, 1.0), b

(2.0, 7.0), b

(8.0, 6.0),

and b

(12.0, 2.0). The control points of the two curve segments B

left

(t)and

right

(t), obtained by cutting B(t) at the parameter value t =0.25, are deter-

mined from the triangle of points computed in Example 6.10. B

left

has control

points b

(1.0, 1.0), b

(1.25, 2.5), b

(1.8125, 3.5625), b

(2.578, 4.25), and B

right

has control points b

(2.578, 4.25), b

(4.875, 6.3125), b

(9.0, 5.0), b

(12.0, 2.0).

Theorem 6.13 (Subdivision)

For a general B´ezier curve B(t)=



i=0

i,n

(t), the control points of

the two curve segments obtained by subdivision at parameter value t are

, b

,...,b

n−1

, b

for B

left

and b

, b

n−1

,...,b

n−1

, b

for B

right

,wherethe

are the points computed in the de Casteljau algorithm (Theorem 6.11).

Proof

Suppose B(t) is subdivided at t = α. The segment B

left

is deﬁned by B

left

(t)=



i=0

i,n

(t) over the interval [0,α]. Thus the curve can be reparametrized

as B

left

(t)=



i=0

i,n

(αt), over the interval [0, 1]. Hence Exercise 6.30 gives

left

(t)=



i=0

⎛

⎝



j=0

i,j

(α)B

j,n

(t)

⎞

⎠



j=0





i=0

i,j

(α)



j,n

(t) .

156 Applied Geometry for Computer Graphics and CAD

Finally, Exercise 6.28 (with k =0)andthefactthatB

i,j

(α) = 0 whenever

i>j,gives

left

(t)=



j=0





i=0

i,j

(α)



j,n

(t)=



j=0

j,n

(t) .

Therefore the segment is deﬁned by control points b

(j =0,...,n)overthe

interval [0, 1] as required.

The result for B

right

follows from an application of the symmetry property

as follows. Substitute t for 1 −t which maps the interval [α, 1] onto the interval

[0, 1 −α]. Apply the result for B

left

with the control points in the reverse order

and with 1 − α in place of α.

EXERCISES

6.32. A cubic B´ezier curve B(t) is given by the four control points

(0.2, 0.0), b

(1.0, 0.4), b

(1.8, 1.2), and b

(3.4, 0.0).

(a) Use the de Casteljau algorithm to evaluate the point B(0.25).

(b) Use the triangular array of points evaluated in part (a) to write

down the sets of control points, deﬁning the segments B

left

and

right

, that are obtained when B(t) is subdivided at t =0.25.

6.33. Plot the curves B(t), B

left

(t), and B

right

(t) obtained in Example 6.12

and verify that the union of the two segments is equal to the original

curve.

6.34. A B´ezier curve B(t) is given by the four control points b

(0.3, 0.1),

(0.9, 0.6), b

(1.3, −0.1), b

(0.7, −0.4).

(a) Use the de Casteljau algorithm to evaluate the point B(1/3).

(b) Write down the control points deﬁning B

left

and B

right

obtained

by subdividing B(t)att =1/3.

6.35. Determine the number of additions and multiplications that are re-

quired to compute the coordinates of one point of a cubic B´ezier

curve by (a) using the de Casteljau algorithm, (b) evaluating the

equation of B(t) (assume that the value of 1 − t is computed just

once). Repeat the calculation for a quartic B´ezier curve. Deduce the

number of additions and multiplications that are required for a gen-

eral B´ezier curve. Is the de Casteljau algorithm the most eﬃcient

method of computing a point?