Marsh D. Applied Geometry for Computer Graphics and CAD
Подождите немного. Документ загружается.


5. Curves 117
Table 5.2 Standard forms for the irreducible conics
Conic Implicit forms Parametric forms
Hyperbola
x
2
/a
2
− y
2
/b
2
=1
a(b
2
+a
2
t
2
)
a
2
t
2
−b
2
,
2ab
2
t
a
2
t
2
−b
2
,t∈ R,t=
b
a
;
±(a cosh θ, b sinh θ) ,θ∈ R ;
(a sec θ, b tan θ) ,
θ ∈
−
π
2
,
π
2
, and θ ∈
π
2
,
3π
2
.
Parabola
y = mx
2
x = my
2
t, mt
2
,t∈ R ;
mt
2
,t
,t∈ R .
Ellipse
x
2
/a
2
+ y
2
/b
2
=1
a(1−t
2
)
1+t
2
,
2bt
1+t
2
,t∈ R ;
(a cos θ, b sin θ) ,θ∈ [0, 2π] .
Theorem 5.15
Let
ˆ
C be the image of the conic C = xMx
T
following the application of a
non-singular planar transformation with transformation matrix A.Then
∆
ˆ
C
=det(A)
2
∆
C
.
So a non-singular transformation does not affect the irreducibility of a conic.
Proof
Let the conic be C = xMx
T
. Then the transformation x = yA yields a conic
ˆ
C =(yA)M(yA)
T
= yAMA
T
y
T
= y
ˆ
My
T
,where
ˆ
M = AMA
T
. Hence
∆
ˆ
C
=det(AMA
T
)=det(A) det(M) det(A
T
)=det(A)
2
det(M)=det(A)
2
∆
C
.
Since A is non-singular, det(A) = 0. Therefore ∆
ˆ
C
= 0 if and only if ∆
C
=0.
Hence C is irreducible if and only if
ˆ
C is irreducible.
The distinctions of hyperbola, parabola, and ellipse apply with respect to a
particular Cartesian coordinate system. The effect on a conic of an application
of an orthogonal change of coordinates (see Exercise 2.21) is expressed by the
following theorem.

118 Applied Geometry for Computer Graphics and CAD
Theorem 5.16
Let
ˆ
C be the image of the conic C (given by (5.7)) following the application of
an orthogonal change of coordinates. Then
b
2
− ac =
ˆ
b
2
− ˆaˆc,
a + c =ˆa +ˆc,
where ˆa,
ˆ
b and ˆc denote the corresponding coefficients of
ˆ
C.
Proof
Let the orthogonal change of coordinates be X =
ˆ
X cos θ −
ˆ
Y sin θ + g
ˆ
W ,
Y =
ˆ
X sin θ +
ˆ
Y cos θ + h
ˆ
W , W =
ˆ
W (expressed in homogeneous coordinates).
Then substituting for X and Y in (5.7) yields
ˆa
ˆ
X
2
+2
ˆ
b
ˆ
X
ˆ
Y +ˆc
ˆ
Y
2
+
ˆ
d
ˆ
X
ˆ
W +ˆe
ˆ
Y
ˆ
W +
ˆ
f
ˆ
W
2
=0
where
ˆa = a cos
2
θ +2b cos θ sin θ + c sin
2
θ,
ˆ
b = b
cos
2
θ − sin
2
θ
+(c − a)sinθ cos θ,
ˆc = a sin
2
θ − 2b cos θ sin θ + c cos
2
θ,
ˆ
d = bg sin θ + e sin θ + bh cos θ + d cos θ + ag cos θ + ch sin θ,
ˆe = ch cos θ − ag sin θ + bg cos θ − bh sin θ − d sin θ + e cos θ, and
ˆ
f = ag
2
+ ch
2
+2dg +2bgh + f +2eh .
Then
ˆ
b
2
− ˆaˆc =
b
cos
2
θ − sin
2
θ
+(c − a)sinθ cos θ
2
−
a cos
2
θ +2b cos θ sin θ + c sin
2
θ
×
a sin
2
θ − 2b cos θ sin θ + c cos
2
θ
= b
2
− ac ,
and
ˆa +ˆc =
a cos
2
θ +2b cos θ sin θ + c sin
2
θ
+
a sin
2
θ − 2b cos θ sin θ + c cos
2
θ
= a + c.

5. Curves 119
Let A be the transformation matrix of an orthogonal change of coordi-
nates. Then, by Exercise 2.21, det(A) = 1. Since
ˆ
b
2
− ˆaˆc = b
2
− ac and
∆
ˆ
C
=det(A)
2
∆
C
= ∆
C
the type of conic is unaffected by a change of co-
ordinates. If (5.4) is multiplied through by a constant µ, then the quantities
a + c, b
2
−ac,and∆ become µ (a + c), µ
2
b
2
− ac
,andµ
3
∆. Thus the ratios
(a + c):
b
2
− ac
1/2
: ∆
1/3
are absolute invariants. A conic expressed in any
rectangular Cartesian coordinate system has the same absolute invariants.
Theorem 5.17
An irreducible conic can be mapped to a conic in standard form by applying
an orthogonal change of coordinates.
Proof
Let the conic be given by (5.7). First, apply a rotation X =
ˆ
X cos θ −
ˆ
Y sin θ,
and Y =
ˆ
X sin θ +
ˆ
Y cos θ. Then (5.7) has the form
ˆa
ˆ
X
2
+2
ˆ
b
ˆ
X
ˆ
Y +ˆc
ˆ
Y
2
+2
ˆ
d
ˆ
X
ˆ
W +2ˆe
ˆ
Y
ˆ
W +
ˆ
f
ˆ
W
2
=0, (5.10)
where the coefficients are given by the expressions in Theorem 5.16, but with g
and h set equal to zero. The
ˆ
X
ˆ
Y term can be eliminated by choosing the angle θ
so that the coefficient
ˆ
b vanishes: the required angle satisfies tan 2θ =2b/(a−c)
if a = c,andθ = π/4or3π/4ifa = c. Provided ˆa =0andˆc = 0, then (5.10)
has the form
ˆa
ˆ
X +
ˆ
d
ˆa
ˆ
W
2
+ˆc
ˆ
Y +
ˆe
ˆc
ˆ
W
2
+
ˆ
f −
ˆ
d
2
ˆa
−
ˆe
2
ˆc
ˆ
W
2
=0.
Applying the translation T
−
ˆ
d
ˆa
, −
ˆe
ˆc
, yields a standard form for the hyperbola
or ellipse given by
ˆa
ˆ
X
2
+ˆc
ˆ
Y
2
+
ˆ
f −
ˆ
d
2
ˆa
−
ˆe
2
ˆc
ˆ
W
2
=0.
If ˆa =0,ˆc = 0, then (5.10) has the form
ˆc
ˆ
Y +
ˆe
ˆc
ˆ
W
2
+2
ˆ
d
ˆ
X
ˆ
W +
ˆ
f
ˆ
W
2
=0.
Applying the translation T
−
ˆ
f
2
ˆ
d
, −
ˆe
ˆc
gives
ˆc
ˆ
Y
2
+2
ˆ
d
ˆ
X
ˆ
W,

120 Applied Geometry for Computer Graphics and CAD
a standard form for the parabola. Similarly, a standard form for the parabola
is obtained when ˆa =0,ˆc = 0. The case ˆa =0,ˆc = 0 is not considered since
the conic is reducible.
Example 5.18
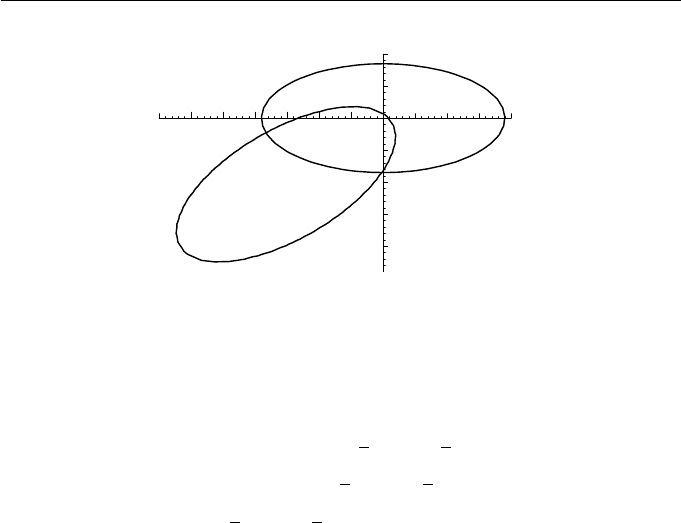
To determine the standard form for the ellipse
2x
2
− 2
√
3xy +4y
2
+5x +6y − 1=0.
Then a =2,b = −
√
3, c = 4, and the required rotation angle is given by
tan 2θ =
√
3, yielding θ = π/6. Then cos(π/6) =
√
3/2, sin(π/6) =
1
2
, and the
required rotation is X =
√
3
2
ˆ
X −
1
2
ˆ
Y ,andY =
1
2
ˆ
X +
√
3
2
ˆ
Y , giving the conic
2
√
3
2
ˆ
X −
1
2
ˆ
Y
2
− 2
√
3
√
3
2
ˆ
X −
1
2
ˆ
Y
1
2
ˆ
X +
√
3
2
ˆ
Y
+4
1
2
ˆ
X +
√
3
2
ˆ
Y
2
+5
√
3
2
ˆ
X −
1
2
ˆ
Y
ˆ
W
+6
1
2
ˆ
X +
√
3
2
ˆ
Y
ˆ
W −
ˆ
W
2
=0.
Simplifying yields
ˆ
X
2
+5
ˆ
Y
2
+
5
2
√
3+3
ˆ
X
ˆ
W +
3
√
3 −
5
2
ˆ
Y
ˆ
W −
ˆ
W
2
=0.
Then, completing the squares in
ˆ
X and
ˆ
Y ,
ˆ
X +
5
4
√
3+
3
2
ˆ
W
2
+5
ˆ
Y +
3
10
√
3 −
1
4
2
−
1+
5
4
√
3+
3
2
2
+
3
10
√
3 −
1
4
2
ˆ
W
2
=0,
and making the translation
¯
X =
ˆ
X +
5
4
√
3+
3
2
ˆ
W ,
¯
Y =
ˆ
Y +
3
10
√
3 −
1
4
ˆ
W ,
¯
W =
ˆ
W gives
¯
X
2
+5
¯
Y
2
−
827
100
+
18
5
√
3
¯
W
2
=0.
In Cartesian coordinates, the standard form of the conic is x
2
+5y
2
=
827
100
+
18
5
√
3
. Figure 5.11 shows the original conic and the computed stan-
dard form conic.
5. Curves 121
–4
–3
–2
–1
1
2
y
–
7
–6 –5 –4 –3 –2 –1
1234
x
Figure 5.11
EXERCISES
5.22. Determine the standard form of the following conics:
(a) 13x
2
− 10xy +13y
2
− 12
√
2x +60
√
2y +72=0.
(b) 6x
2
+12xy +6y
2
− 35
√
2x − 37
√
2y + 118 = 0.
(c) 11x
2
− 6x
√
3y − 6x
√
3+y
2
+2y − 63 = 0.
5.23. Determine the absolute invariants of the standard forms. Compute
the absolute invariants for each of the conics of the previous exercise,
and verify that the computed standard form has the same invariants.
5.24. Use Exercise 5.18 to show that a conic with eccentricity >0isa
hyperbola if >1, an ellipse if <1, or a parabola if =1.
5.25. Show that a translation leaves the values of a, b, c unaltered. These
quantities are called translational invariants.
5.6.3 Intersections of a Conic with a Line
The points of intersection of a conic and a line are found by a process of
elimination of variables to give a quadratic polynomial equation in one of the
variables. The equation is solved, and backward substitution of the solutions
is used to determine the points of intersection. The derivation of the quadratic
depends on whether the conic and the line are given in implicit or in parametric
form. The procedure is explained by means of examples.
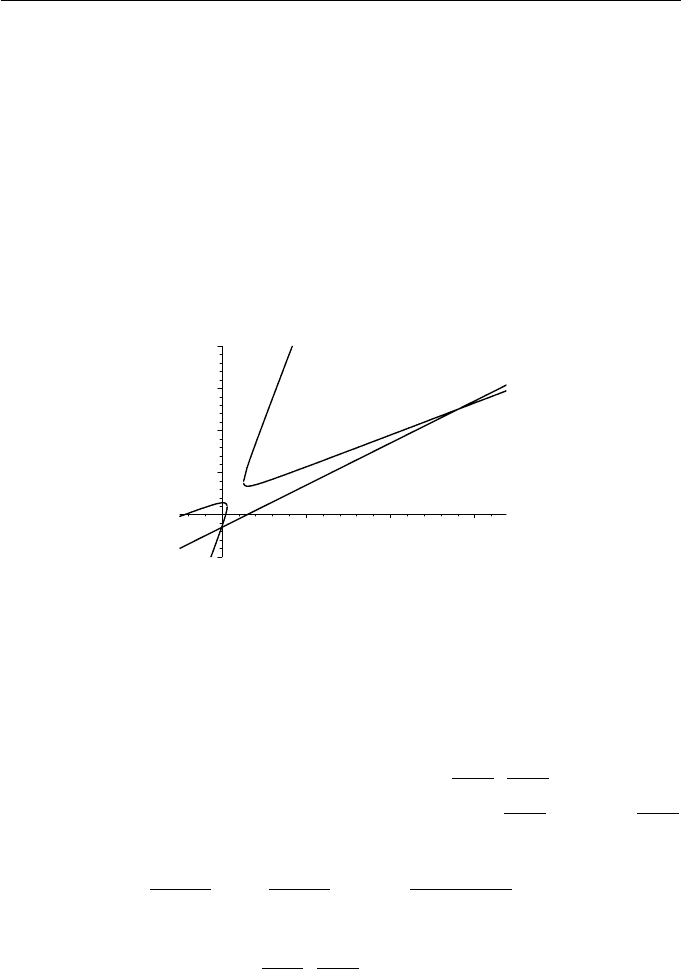
122 Applied Geometry for Computer Graphics and CAD
Example 5.19
To find the intersections of the conic x
2
− 3xy + y
2
+4x − 2 = 0 and the line
parametrized by (x(t),y(t)) = (2t +1,t− 1), shown in Figure 5.12, substitute
x =2t +1 andy = t − 1 into the conic equation to give
(2t +1)
2
+(t − 1)
2
− 3(2t +1)(t − 1) + 4(2t +1)− 2=−t
2
+13t +7=0.
The solutions are approximately t = −0.518 and t =13.518. Substituting the
values of t into the parametric equation (x(t),y(t)) = (2t +1,t− 1) gives the
two points of intersection (−0.036, −1.518) and (28.036, 12.518).
–5
0
5
10
15
20
10 20 30
Figure 5.12 Intersection of conic x
2
− 3xy + y
2
+4x − 2 = 0 and line
(2t +1,t− 1)
Example 5.20
To find the intersection of the conic (x(t),y(t)) =
3t+t
2
1+2t
2
,
3t
1+2t
2
with the line
2x + y + 1 = 0, shown in Figure 5.13(a), substitute x =
3t+t
2
1+2t
2
and y =
3t
1+2t
2
into the equation of the line to give
2
3t + t
2
1+2t
2
+
3t
1+2t
2
+1=
4t
2
+9t +1
1+2t
2
=0.
The solutions of 4t
2
+9t + 1 = 0 are approximately t = −2.133 and t =
−0.117. Substituting for t in
3t+t
2
1+2t
2
,
3t
1+2t
2
yields the two points of intersection
(−0.183, −0.634) and (−0.329, −0.342).
Example 5.21
To determine the intersection of the line x + y − 1 = 0 and the conic

5. Curves 123
–1
–0.5
0
0.5
1
–1 –0.5 0.5 1 1.5
–
4
–2
0
2
4
y
–
5
–4 –3 –2 –1 1 2 3 4
x
(a) (b)
Figure 5.13 (a) Intersection of conic
3t+t
2
1+2t
2
,
3t
1+2t
2
and line 2x+y+1 = 0,
and (b) intersection of conic x
2
− 2xy +3y − 7 = 0 and line x + y − 1=0
x
2
− 2xy +3y − 7 = 0, shown in Figure 5.13(b), substitute y =1− x into
the conic equation to give
x
2
− 2x (1 − x)+3(1− x) − 7=3x
2
− 5x − 4=0.
Solving yields x = −0.591 and x =2.257. Substituting the solutions into
y =1− x yields the points (−0.591, 1.591) and (2.257, −1.257).
If both the line and the conic are expressed in parametric form, then the
line is converted to implicit form, and the method of Example 5.20 is applied.
EXERCISES
5.26. Find the points of intersection of the following conics and lines:
(a) conic 9x
2
− xy + y
2
− 4x +2y + 1 = 0, line (x(t),y(t)) = (2t −
3, −3t +4).
(b) line x +3y − 6 = 0, conic 3x
2
− 2xy + y
2
− 5x +6y − 16 = 0.
(c) line −2x +5y + 7 = 0, conic (x(t),y(t)) = (3t
2
−4t +1, 2t
2
−9t).
(d) line (t +1,t− 1), conic x
2
+2xy + x − y − 1=0.
(e) line −3x − 2y + 4 = 0, conic (t
2
+1,t− 1).
5.27. The conic segment (x(t),y(t)) = (3t
2
− 4t − 1, 2t
2
− 9t + 10), t ∈
[−1, 4] is to be clipped by the rectangle with bottom left corner
at (0, 0) and upper right corner (20, 20) as shown in Figure 5.14.
The clipping operation removes the parts of the conic contained
outside the rectangle. Determine the parameter values where the
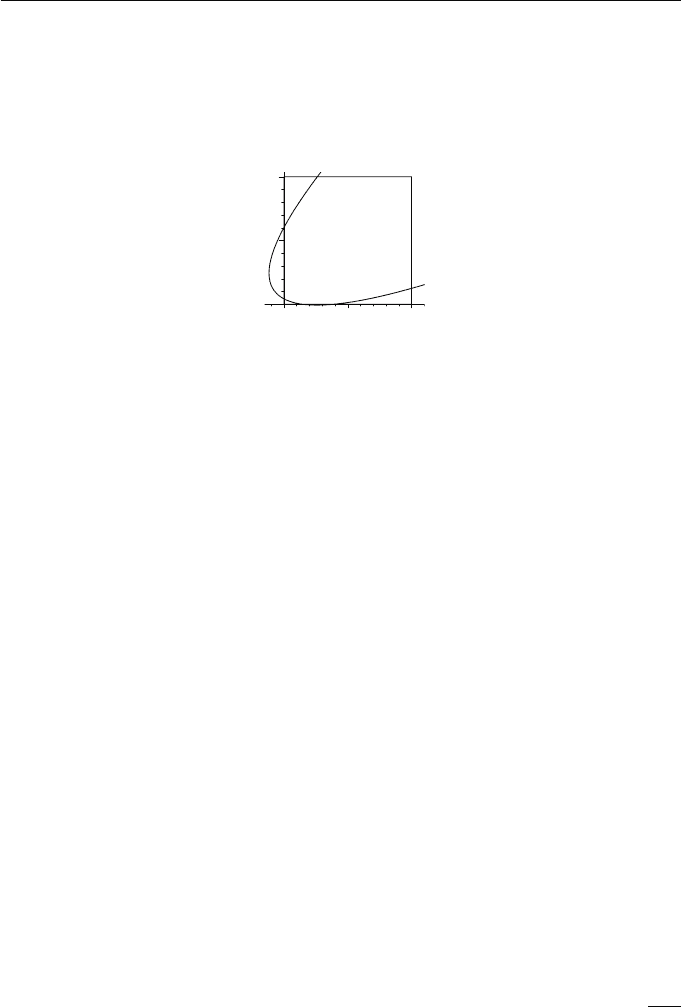
124 Applied Geometry for Computer Graphics and CAD
conic intersects each side of the rectangle. For each conic segment
inside the rectangle, determine the parameter interval on which it is
defined. For any parametrized conic, what is the maximum number
of segments that arise following a rectangular clipping operation?
10
20
1
0
2
0
0
0
Figure 5.14
5.6.4 Parametrization of an Irreducible Conic
An irreducible conic C(x, y) = 0 can be parametrized by performing the fol-
lowing steps.
1. Determine a point P(p
1
,p
2
) on the conic.
2. Consider the family of lines y =(x−p
1
)t+p
2
, parametrized by t, consisting
of all lines in the plane through P. Each parameter value t corresponds to
a line in the family.
3. Determine the points of intersection of the line y =(x − p
1
)t + p
2
and the
conic as follows. Substitute y =(x − p
1
)t + p
2
in C(x, y)=0togivea
quadratic polynomial (dependent on t) q
t
(x) = 0. The roots of q
t
(x)=0
are the x–coordinates of the intersection points. Since P(p
1
,p
2
) is known to
be an intersection point of the conic and every line in the family, it follows
that x = p
1
is a root of q
t
(x). Hence x − p
1
is a factor of q
t
(x).
4. Factorise q
t
(x)as(x − p
1
)(β(t)x − α(t)) for some quadratic polynomials
α(t)andβ(t). Then the second root of q
t
(x)=0isx = α(t)/β(t), giving the
x-coordinate of the other point of intersection as a function of t: x = x(t).
5. Substitute x = α(t)/β(t)iny =(x − p
1
)t + p
2
to give y = y(t).
6. It follows that (x(t),y(t)) parametrizes the conic, since every point Q on
the conic, distinct from P, is the intersection of the conic and the line
PQ
through P.
Different choices of the point P will give rise to alternative parametrizations of
the conic.

5. Curves 125
Example 5.22
Find a parametrization of the hyperbola −2x
2
− 5xy +4y
2
+ x − 5y +15=0
by considering lines through the point (2, 3).
It is easily checked that (2, 3) is a point on the conic. The family of lines
through (2, 3) is given by y = t (x − 2) + 3. Substituting for y in the equation
of the conic gives
−2x
2
− 5x (t (x − 2) + 3) + 4 (t (x − 2) + 3)
2
+ x − 5(t (x − 2) + 3) + 15 = 0 ,
which factorizes as
(x − 2)
−2x − 5tx +4t
2
x − 8t
2
+19t − 18
=0.
Solving for x yields x =2and
x =
18 − 19t +8t
2
−2 − 5t +4t
2
. (5.11)
The solution x = 2 corresponds to the known intersection (2, 3). Using (5.11)
to substitute for x in y = t (x − 2) + 3 gives
y = t
18 − 19t +8t
2
−2 − 5t +4t
2
− 2
+3=
−6+7t +3t
2
−2 − 5t +4t
2
.
It follows that
(x(t),y(t)) =
18 − 19t +8t
2
−2 − 5t +4t
2
,
−6+7t +3t
2
−2 − 5t +4t
2
is a parametrization of the conic. The values of t for which the denominator
vanishes are the solutions of 4t
2
− 5t − 2 = 0, that is, t = −0.319 and t =
1.569. Therefore the curve is defined on the parameter intervals (−∞, −0.319),
(−0.319, 1.569), and (1.569, ∞). Each interval corresponds to a branch or a
part of a branch of the conic.
Example 5.23
Find a parametrization of the conic C(x, y)=x
2
−2xy +4y
2
+2x + y +1=0.
First determine a point on the conic. One way to do this is to find an
intersection of the conic with one of the axes. If this fails one can try intersecting
with other lines parallel to one of the axes. Set y =0inC(x, y)=0.Then
x
2
+2x +1= 0. Thus x = −1. Hence (−1, 0) is a point on the conic. Next

126 Applied Geometry for Computer Graphics and CAD
consider the family of lines y =(x +1)t through (−1, 0). Substituting y =
(x +1)t in C(x, y) = 0, gives
x
2
− 2x(x +1)t +4((x +1)t)
2
+2x +(x +1)t +1=0,
and factorizing gives
(x +1)
−2xt +4t
2
x + x +1+4t
2
+ t
=0.
Each line in the family intersects the conic in two points: (−1, 0) and one other.
Setting the second factor equal to zero, and solving for x, gives the x-coordinate
of the unknown intersection point
x = −
4t
2
+ t +1
4t
2
− 2t +1
.
The y-coordinate is obtained by substituting for x in y =(x +1)t giving
y =
−
4t
2
+ t +1
4t
2
− 2t +1
+1
t = −
3t
2
4t
2
− 2t +1
.
Thus the conic is defined parametrically by
(x(t),y(t)) =
−
4t
2
+ t +1
4t
2
− 2t +1
, −
3t
2
4t
2
− 2t +1
.
The denominator 4t
2
− 2t + 1 does not vanish for real values of t, and hence
the parametrization is defined for all t.
EXERCISES
5.28. Determine another parametrization of the conic x
2
− 2xy +4y
2
+
2x + y + 1 = 0 of Example 5.23 by considering lines through the
point (−2, −1).
5.29. Convert the following conics from implicit to parametric form:
(a) x
2
+2y
2
− 2xy +2y = 0; consider lines through (0, 0).
(b) x
2
− 2xy +5y
2
− 2x +3y +1=0.
(c) x
2
+2xy − y
2
− 1=0.
(d) 2x
2
− y
2
+4x − 2y =0.
