Малыхин В.И. Математика в экономике

Подождите немного. Документ загружается.

262

(в

скобках);

Ц1),

2(2),

3(3),

4(4),

5(5),

6(3), 7(2).

Видим,

что

вариантов

немного,

значит, будем строить ДВР:

т—

rf- rf-

-£-

=f-

rf-

r?-

У20

/20

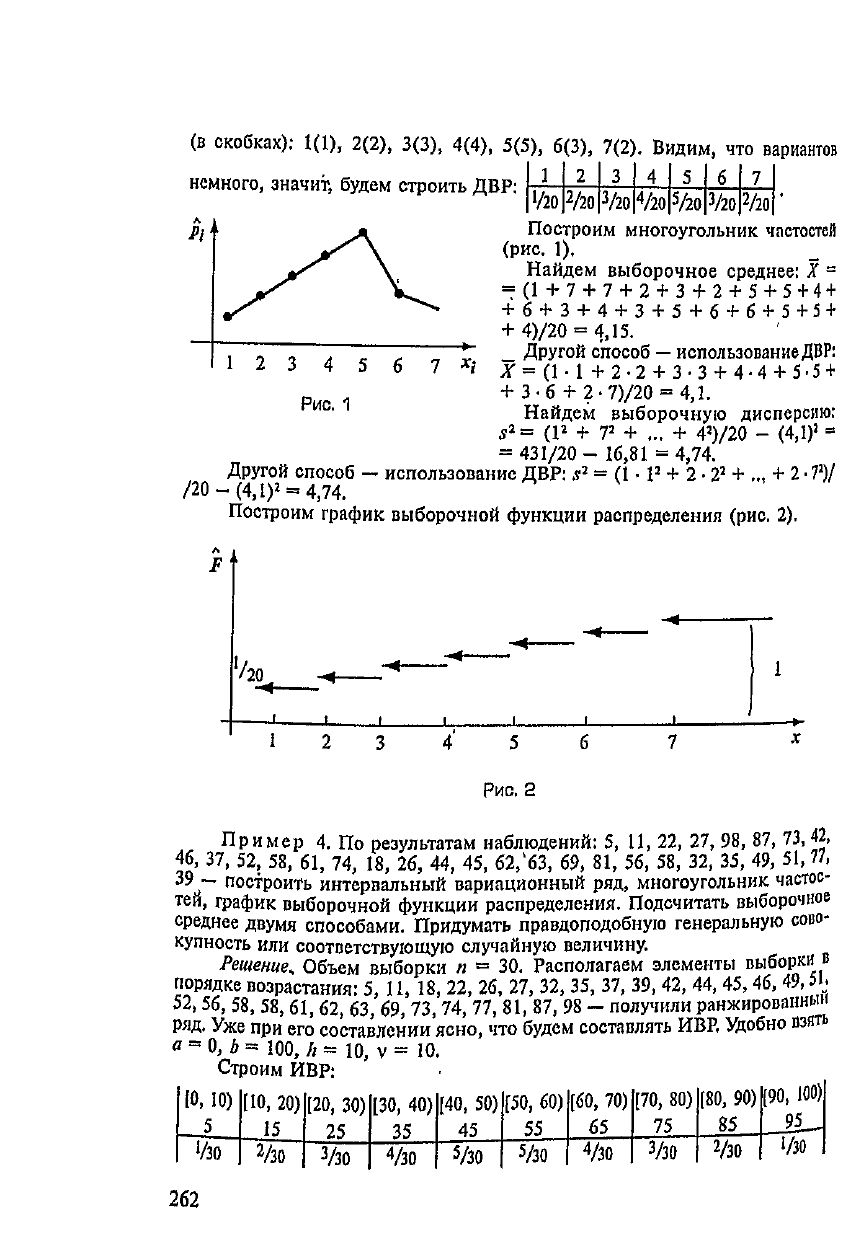
Построим многоугольник

частостсй

(рис.

1).

Найдем выборочное среднее;

(1+7

+ 7 + 2 + 3 + 2 + 5 + 5 + 4 +

+ 3 + 4 + 3 + 5 + 6 +

+ 5+5 +

4)/20

4,15.

Другой способ

—

использование

ДВР:

ЛГ=(Ы

+2-2

3-3

4-4

5-5

3-б

2.7)/20

4,1.

Найдем

выборочную

дисперсию:

...

4')/20

(4,1)'

431/20-

16,81

=4,74.

Другой

способ

—

использование

ДВР:

= (1 •

+ 2 •

+ .., + 2 •

/20

-(4,1)*-4,74.

Построим график выборочной функции распределения (рис.

2),

Рис.

Пример

4. По

результатам наблюдений:

П,

22, 27, 98, 87, 73, 42,

46,

37, 52, 58, 61, 74, 18, 26, 44,

45,

62/63,

69,

81,

56, 58, 32, 35, 49, 51, 77,

39 —

построить интервальный вариационный

ряд,

многоугольник

частос-

тей,

график выборочной функции распределения. Подсчитать

выборочное

среднее

двумя способами. Придумать правдоподобную

генеральную

сово-

купность

или

соответствующую случайную величину.

Решение^

Объем выборки

- 30.

Располагаем

элементы

выборки»

порядке

возрастания:

11,

18,

22, 26, 27, 32, 35, 37, 39, 42, 44, 45, 46,

49,51.

52,56,

58, 58, 61, 62, 63, 69, 73, 74, 77, 81, 87, 98 -

получили

ранжированный

РЯД.

Уже при его

составлении

ясно,

что

будем составлять

ИВР.

Удобно

взять

*«

100,

10,

10.

Строим

ИВР:

[0.

Ю)

[10,

20)

[20,

30)

[30,

40)

[40,

50)

[50,

60)

[60,

70)

[70,

80)

[80,

90)

[90,

15 25 35 45 55 65 75 85

_9L_

'/30

2/30

З/зо

4/зо

V30

/30

'/30

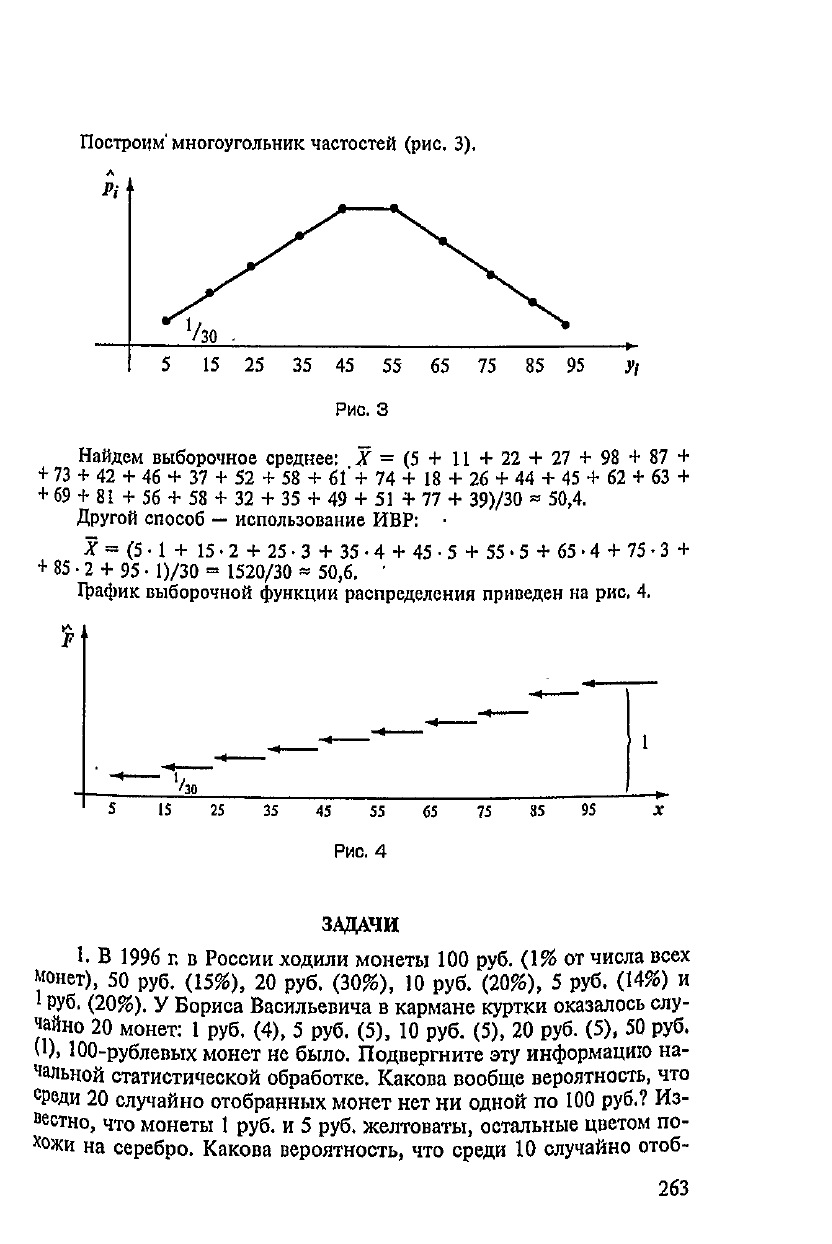
Построим'

многоугольник

частостей

(рис.

3).

Рис.

Найдем выборочное

среднее;

X = (5

+ 22 + 27 + 98 + 87 +

73 + 42 + 46

37 + 52 + 58 +

61'

+ 74 +

+ 26 + 44 + 45

+ 63 +

69 + 81 +

+ 58 + 32 + 35 + 49 + 51

77 +

39)/30

50,4.

Другой способ

—

использование

ИВР:

•

1 + 15

•

2 + 25 • 3 + 35

•

4 + 45 • 5 + 55 - 5

65 • 4 +

• 3

•

2 + 95 •

1)/30

1520/30

50,6.

Трафик

выборочной функции распределения приведен

на

рис,

Рис.

ЗАДАЧИ

1996

г. в

России ходили монеты

100

руб.

(\%

от

числа всех

монет),

руб,

(15%),

руб.

(30%),

руб.

(20%),

руб. (14%)

Руб. (20%).

Бориса Васильевича

кармане куртки оказалось слу-

чайно

монет:

руб. (4),

руб. (5),

руб.

(5),

руб. (5),

руб.

U),

100-рублевых монет

не

было. Подвергните

эту

информацию

на-

чальной

статистической обработке. Какова вообще вероятность,

что

Реди

случайно отобранных

монет

нет ни

одной

по 100

руб.?

Из-

вестно,

что

монеты

руб.

и 5

руб.

желтоваты,

остальные цветом

по-

*°жи

на

серебро. Какова вероятность,

что

среди

случайно

отоб-

263

ранных

монет

«серебряных»

нет?

Как

поведут себя

вероятности,

которых

только

что

было

спрошено,

при

увеличении числа

отобран-

ных

монет?

Решение,

Найдем только вероятность того,

что

среди

случай-

но

отобранных

монет

нет ни

одной 100-рублевой.

Она

равна

I/100)

(1 -

i/lOO)

100

'"/

е-'-

0,8.

Очевидно,

что в

примере

2 в

результате обработки

анкет

был

построен

фактически ИВР. Найдите нижнюю

верхнюю

границы

для

элементов выборки,

т.е.

а и

Ь,

длины

интервалов,

интервальные

частости

достройте ИВР. Постройте график эмпирической

функ-

ции

распределения, определите выборочное среднее.

Размер обуви взрослого мужчины

есть,

очевидно,

д.с.в.

воз-

можными

значениями, скажем

от 35 до 50.

Представьте,

что вы

про-

вели

обследование

этой

с.в. Постройте примерный

ДВР для

нее.

На

основании

ДВР

найдите средний размер, постройте

эмпирическую

функцию

распределения

и ее

график. Какой смысл имеет

эта

функ-

ция

распределения?

Денежная сумма, которую оставляет покупатель

магазине,

является

случайной. Придумайте правдоподобный

ИВР для

этой

с.в-

На

основании

ИВР

найдите средний размер, постройте

эмпиричес-

кую

функцию распределения

и ее

график.

Какой

смысл

имеет

эта

функция

распределения?

Тема

17.

НОРМАЛЬНЫЙ ЗАКОН.

ПРЕДЕЛЬНЫЕ

ТЕОРЕМЫ

И ИХ

ПРИМЕНЕНИЯ

17.1.

НОРМАЛЬНЫЙ

ЗАКОН,

ЗАКОН

БОЛЬШИХ

ЧИСЕЛ,

ПРЕДЕЛЬНЫЕ

ТЕОРЕМЫ

Нормальный

закон

параметры

его

задания. Этот

закон

играет

теории

вероятностей

математической статистике

выдающуюся

С.в.

называется

распределенной

по

нормальному закону

пар

метрами

а и а > 0,

если

;Г

имеет

плотность распределения

вероя™

стей

(график

ее

представлен

на

рис.

1);

Лх)-(\/(а^№~

(х

-°

264

Как

видно,

с.в.,

распределенная

по

нормальному закону, является

не-

прерывной

с.в.

Выясним смысл параме-

тров

а и

о*.

По

определению

матема-

+00

тического

ожидания

М[Х[

]xf(x)dx

—со

+со

(1/(стУ2я))е-<*

-tf№>dx.

Замена переменной

х - а = и

—со

+00

сводит

этот

интеграл

сумме двух

— J

(м/(а

/гтс")^-"^

201

I—СО

(а/(ст

V2rc))e-"W)ciH.

Первый

интеграл,

очевшито,

равен

нулю.

Что

-00

+00

касается

второго,

то он

равен

a J

(1/(ст

^Тк^ъ-^^&и.

Если учесть,

—-со

что

(1/(ау2тс))е"

2/(2

есть плотность нормального распределения

+СО

параметрами

0 и

сг,

то

интеграл

(l/(<j/2^))e-"

(2a3)

есть интеграл

—оо

<я

этой плотности, следовательно,

он

равен единице.

Значит,

мате-

матическое

ожидание равно

а.

Вычисление дисперсии

ЛГдает

резуль-

тат;

D[X\

следовательно,

ст

*lD[X\.

Итак, параметр

есть сред-

нее

квадратическое

отклонение

с.в.

То,

что X

есть

с.в.,

распределенная

по

нормальному закону

параметрами

а и ст,

обозначают также так;

X е

N(a,

a).

При

вычислении вероятностей такая

с.в.

сводится

с.в.

*е

Л^(0,

1).

Действительно, пусть

—

функции распределения

Для

соответственно,

тогда

(t)

(l/(a

У27Г))е-

(н

0)ЗА2

М«;

де-

—со

265

лая

замену переменной

(«

а)/а

у,

получим:

Fjffi

F£(t

о)/о).

Поэтому

для

любых

а < В

имеем:

Р(а

< X < В) =

.Л/В)

FJa)

^(р-

)/а)-^(а-

)/а).

Итак, знание функции распределения

Т^для

с.в.

tf(0,1}

позволяет находить всевозможные вероятности

и для

других нор-

мально

распределенных с.в. Большее распространение,

чем

на-

шла,

однако, функция Лапласа:

Ф(/)

l/-/2jT)e-^

dw,

Так как

оче-

видно,

что

/^0)

(\/</2n)er#fl

1/2

силу четности

подынте-

_-со

гральной

функции,

то

Ф(/)

F£t}

1/2.

Следовательно,

для X

N(a

ст)

имеем:

Да < X <

р)

Ф((Р

д)/с)

Ф((а

д)/о).

Итак,

нахождение всевозможных

вероятнос-

тей

для

нормально распределенных с.в. свелось

функции

Лапласа.

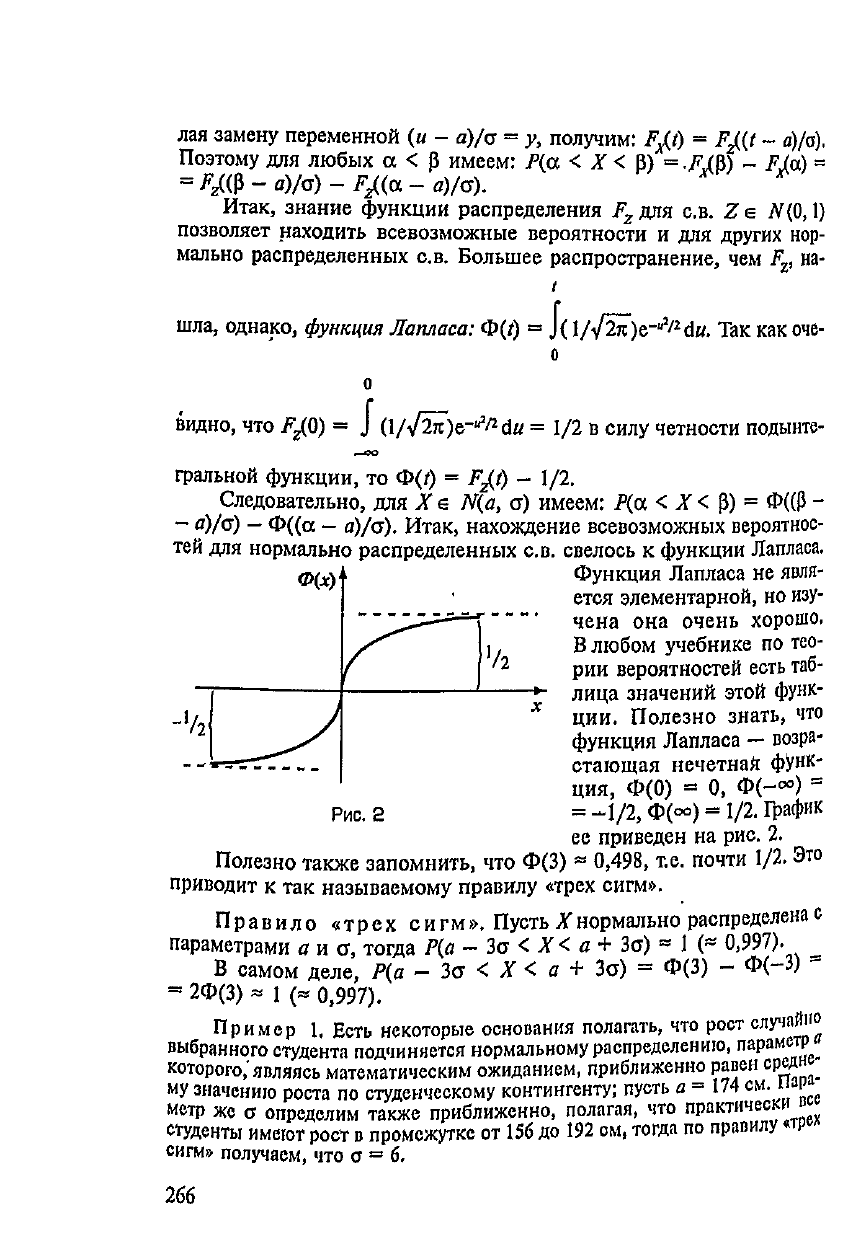
Функция

Лапласа

не

явля-

ется

элементарной,

но

изу-

чена

она

очень

хорошо,

любом учебнике

по

тео-

рии

вероятностей

есть

таб-

лица

значений этой

функ-

ции. Полезно знать,

что

функция

Лапласа

—

возра-

стающая нечетная

функ-

ция,

Ф(0)

=»

О,

Ф(-°°)

-1/2,

Ф(оо)=

1/2.

График

ее

приведен

на

рис.

Полезно также

запомнить,

что

Ф(3)

0,498,

т.е.

почти

1/2.

Это

приводит

к так

называемому правилу «трех сигм».

Правило

«трех

сигм».

Пусть

Анормально

распределена

параметрами

она,

тогда

Р(а

- За <

Х<

За)

(»

0,997).

самом

деле,

Р(а

Зст

< X < а + За) =

Ф(3)

Ф<-3)

2Ф(3)

* 1

0,997).

Пример

Есть некоторые

основания

полагать,

что

рост

случайно

выбранного

студента подчиняется нормальному

распределению,

параметр

которого,"

являясь математическим ожиданием, приближенно равен

среди

му

значению роста

по

студенческому контингенту; пусть

а - 174 см.

метр

же

определим

также приближенно, полагая,

что

практически

студенты

имеют

рост

промежутке

от

156

до 192 см,

тогда

по

правилу

*Ф*

сигм»

получаем,

что а

б,

266

Итак,

рост

ТЕ

N(174,

б).

Найдем

вероятности

Р(Т> 180), Р(Т<

\Щ

}

Р(№<

Т<

190).

Решение.

Для

вычисления

указанных

вероятностей

применяем

форму-

лу

/>(сс

< Т < Р) =

Ф((р

174)/6)

Ф((а

174/6)

получаем:

?(180

< 7)

/>(180

Г<

оо)

1/2

Ф«180

174)/б)

1/2

0,34

0,16;

Р(Т<

190)

Ф((190

174/6)

Ф(-оо)

ф(1б/б)

1/2

0,996;

Р(№

< Т <

190)

Ф((190

174)/б)

Ф((160

174/6)

Ф(1б/б)

Ф(14/б)

0,496

0,489

0,985.

Закон больших чисел.

узком смысле

под

«законом

больших

чисел»

понимается

ряд

математических

теорем,

которые утверждают

приближение

средних характеристик большого числа опытов

к не-

которым

постоянным величинам.

широком смысле

этот

закон

ут-

верждает,

что при

очень большом числе случайных явлений

средний

их

результат перестает

'быть

случайным

может быть предсказан

большой

степенью определенности.

Для

доказательства важных теорем закона больших чисел необ-

ходимо

ознакомиться

неравенством Чебышева.

Неравенство

Чебышева.

Пусть

Xесть

с.в,

математичес-

ким

ожиданием

дисперсией

Тогда

для

любого

е > 0

вероят-

ность

того,

что

с.в.

^отклонится

от

своего математического ожида-

ния

больше

чем на е,

ограничена сверху величиной

DJ&'.

W-mJ>e)

/е

Доказательство.

Для

упрощения

предположим,

что

с.в.

X X

Дискретная

и ее ряд

распределения

есть

•—•

•••

•—•••.

Р\

У\

По

определению,

D[X\

ЩХ-

«/]

£(*,

т/р,.

Опустим

часть

слагаемых

этой

сумме,

тогда

получим

неравенство

(*/

)*р

Заменяя

(х,

)

на

мы

лишь усилим

|*,-и,|>е

неравенство:

/>,

или

Но

р,

\х,

-т

>е

~m.

1-х,

-т,|

>е

есть

вероятность

Р(\Х-

> е),

значит,

Д^

&Р(\Х-

/«J

> е) и,

деля

обе

части последнего неравенства

на

получаем неравенство Чебы-

шева.

силу своей общности неравенство Чебышева малопригодно

практических

надобностей

— оно

дает

слишком

грубую оценку.

Пусть,

например,

^равномерно

распределена

на

отрезке

[0,10],

тог-

100/12

8,3

(см.

п. 5,

раздел

16.3).

Оценим

с по-

267

мощью

неравенства

Чебышева

вероятность отклонения

ЛГот

своего

математического ожидания, т.е.

от 5,

больше

чем на

0,5.

Имеем;

Р(\Х-

0,5)

/Q,25

—

33,2. Легко подсчитать,

что

оцениваемая

вероятность

равна 9/10,

Так как

9/10

36,

то

неравенство

Чебышева

верно

(в

данном случае оно, конечно, верно

уже

потому,

что

любая

вероятность

не

больше единицы),

Переходя

дополнительному событию, получаем другую

форму

неравенства

Чебышева;

Д(|ЛГ-лд<е)

> 1 -

DJ/&.

На

неравенство Чебышева опирается теорема,

связанная

также

с его

именем.

Теорема

Чебышева.

Пусть

есть с,в.

математическим

ожиданием

а и

дисперсией

Будем проводить серии

из п

независи-

мых

опытов

вычислять среднее арифметическое

значений,

при-

нятых

с.в.

А'в

таких сериях. Тогда

для

любого

е > О

"p(\Y

—

а\

> е)

0 При Л

-»

оо,

Прокомментируем

эту

теорему.

Заметим,

что

если

проводить

се-

рии

из п

опытов,

то от

серии

серии величина

будет

меняться,

т.е.

она

является случайной. Таким образом, значение

совсем

не

обязательно

совпадет

математическим ожиданием

X, а

будет

отли-

чаться

от

него,

Однако намного

ли и как

часто? Теорема

Чебышева

как

раз

утверждает,

что

вероятность

больших отклонений

среднего

арифметического

с.в.

Л'от

его

математического ожидания

стремится

нулю

при

росте длины серий.

Так что

если

мы

хотим

быть

более

уверенными

том,

что

среднее арифметическое

приближение

равно

математическому

ожиданию,

мы

должны увеличить число

опытов.

Доказательство теоремы Чебышева. Обозначим значение, при-

нятое

X в

/-м

опыте через

Тогда

(£

Х)/п.

По

свойствам

ма-

ЕЗ

тематического ожидания имеем:

M[YJ

(1/я)

М^/1-

Но все

с.в.

"**

I,.,.,

распределены

как

с.в.

так что

ЩХ)

М[Х\

~ан

потому

МУ,]

а. Так как

опыты проводятся независимо,

то

с.в.

^независи-

мы,

значит,

по

свойствам дисперсии имеем:

£Щ

(1/п

)

-°W

/са]

d/n.

Теперь применим

неравенство

Чебышева

для

с.в.

P(K

ЩУ,У\

> е)

Д)д/е

или

P(\Y

ЩУ$

> е)

rf/(«e

Так

как

(1/(п&)

0 при п

-»

ее,

то и

P(\Y

а][>

е)

0 при п

°°-

Из

теоремы Чебышева вытекает другая теорема.

268

Теорема

Бернулли.

Пусть

событие

имеет

вероятность/?.

Будем

проводить серии

из

независимых опытов

вычислять

часто-

ту

7„

наступления события

А в

таких

сериях.

Тогда

для

любого

е > О

А|У„

Р\

> е)

0 при п

оо.

Доказательство.

По

событию

определим

с.в.

которая

равна

единице,

если

произошло,

нулю,,если

А не

произошло.

Тогда

ЩХ\

Р»

ЩХ\

—

PQ-

Определенная

доказательстве теоремы

Чебы-

шева

с.в.

есть

не что

иное,

как

частота

у,

наступления события

серии.

Следовательно,

по

теореме

Чебышева

получаем:

Д|у„

— р\ >

Е)

0 ПрИ

со.

Теорема

Бернулли

—

одна

из

центральных

теории вероятнос-

тей,

ведь

она

устанавливает точную связь между частотой

вероят-

ностью

события. Прокомментируем

эту

теорему.

Заметим,

что

если

проводить

серии

из п

опытов,

то от

серии

серии частота

у„

будет

меняться,

т.е.

она

является случайной величиной. Таким

образом,

ее

значение

совсем

не

обязательно совпадет

вероятностью

события.

Теорема

Бернулли

как раз

утверждает,

что

вероятность больших

от-

клонений

частоты случайного события

от его

вероятности стремится

нулю

при

росте длины серий.

Так что

если

мы

хотим быть более

Уверены

том,

что

частота приближенно равна вероятности собы-

тия,

мы

должны увеличить число опытов.

Центральная

предельная

теорема

и ее

следствия.

Эта

теорема

Устанавливает

предельное распределение сумм большого числа с.в.

Простейшая

форма этой теоремы такова.

Центральная

предельная

теорема

(ЦПТ).

Пусть^,...,

-fy

... —

независимые

одинаково распределенные

с.в.,

тогда

при

-»

оо

закон распределения суммы

^неограниченно

при-

ближается

нормальному. Более точно,

при п

°°

равномерно

по

ее

имеем:

Да <

(Z-

na)/(<s

Jn)

< р)

-»

Фф)

Ф(а),

где

G-

математическое

ожидание

среднее

квадратическое отклонение

-в.

а Ф —

функция Лапласа.

Это

значит,

что

закон распределения с.в.

па)/(<5

уя)

не-

ограниченно

приближается

нормальному закону

параметрами

0,1.

Ит

ак,

при

большом числе складываемых независимых

одинаково

Распределенных

с.в. закон

их

распределения приближенно

можно

считать

нормальным.

269

Пример

Количество тонн цемента, взятое

за

день

цементного

склада,

является

с.в.

рядом распределения

тгтгтг

. С

какой

вероят-

ностью

2000

цемента хватит

на

квартал

— 90

дней?

Решение. Обозначим через

Л)

случайное количество цемента,

взятое

/-и

день

со

склада. Будем считать,

что все эти

величины

независимы

оди-

наково

распределены

вышеуказанным рядом распределения.

Тогда

их ма-

тематическое

ожидание равно

20, а

дисперсия

200.

соответствии

ЦПТ

закон

распределения

их

суммы

за

квартал

—

приближенно

нормальный

параметрами:

M[Z

]

- 90 • 20 =

1800,

D[Z

= 90 • 200

18000

о>^

/А^ЙГ-

134.

Следовательно,

P(Z

2000)

Ф((2000

1800)/134)

1/2 *

0,93.

Следствием

ЦПТ

является следующая

теорема.

Интегральная

теорема

Муавра—Лапласа.

Пусть

со-

бытие

имеет вероятность

р.

Будем проводить серии

из

независи-

мых

опытов

подсчитывать число

наступления события

Л в

таких

сериях.

Тогда

при

брльшом

P(k

)

Ф((А

np)/Jnpg)

Ф«Л,

л/ОЛ/w)'

Для

доказательства отметим

только,

что

число

можно

предста-

вить

суммой

независимых

одинаково распределенных

с.в.,

после

чего

надо воспользоваться

ЦПТ.

Пример

3. При

изготовлении отливок

получается

2Q%

дефектных,

Сколько

необходимо

запланировать

отливок

изготовлению,

чтобы

веро-

ятностью

0,95

получилось

не

менее

бездефектных?

Решение, Воспользуемся интегральной теоремой

Муавра—Лапласа.

Имеем

4/5,

значит,

1/5,

Р(50

А)

0,95,

а п

неизвестно,

его и

надо

найти.

другой стороны,

Р(50

А) = 1/2 -

Ф(н),

где и

(50 -

np)/fnM'

Следовательно,

Ф(н)

-0,45.

По

таблице значений

функции

Лапласа

нахо-

дим:

-1,64,

Итак,

(4л/5

- 50)

1,64

^4п/25.

Решая

это

уравнение,

получаем:

69,

ЗАДАЧИ

Как

выглядит правило «трех сигм»

для

произвольной

с.в..

Ответ. Воспользуемся неравенством

Чебышева:

Р(\Х

ScJ

> 1 -

ДЛК>>

W-

«J

3а

окончатель

но

получаем

Р(\Х

За

)

8/9.

С.в.

^распределена

по

нормальному закону

параметрами

Найдите вероятности

ДГ>

1),

Д2

^Г<

5),

Р(

х<

?(Х=

3).

Напишите функции плотности

распределения

постро

те их

примерные графики.

Как

выглядит

для

данной

с.в.

прав

«трех

сигм»-?

270

Банкомат выдает стандартные суммы

в 500

дол.,

100

дол.

дол.,

причем первые составляют лишь

10%,

последние

60%

всех

выдач.

сутки банкомат осуществляет примерно

100

выдач. Сколь-

ко

же

долларов надо заложить

банкомат утром, чтобы

до

следую-

щего

утра

их

хватило

вероятностью,

не

меньшей

0,9?

4. В

районе

универсамов, примерно одинаковых. Суммарная

суточная

выручка

в них

равна

среднем

10 млн

руб.

и в 90%

всех

случаев

отличается

от 10 млн

руб.

не

более

чем на 1 млн

руб. Найди-

те

вероятности

того,

что

очередная суточная суммарная выручка:

а)

превысит

12 млн

руб.;

б)

окажется меньше

9 млн

руб.;

в)

окажется

пределах

от 8 до 12 млн

руб,

Станок

для

изготовления

ДСП

разрегулирован

выпускает

плиты,

толщина которых нормально распределена

N (22 мм, о -

1 мм)

вместо

#(20

мм,

<т'~

мм). Каков

процентах перерасход

сырья?

Каков процент брака

(брак

— это

выход

за

отклонение

мм)? Предложите способ убедиться

том,

чти

станок разрегулиро-

ван.

17.2.

ПРИМЕНЕНИЯ

ЗАКОНА

БОЛЬШИХ

ЧИСЕЛ

ЦЕНТРАЛЬНОЙ

ПРЕДЕЛЬНОЙ

ТЕОРЕМЫ

Усреднение

влияния

независимых факторов. Закон больших

чи-

сел

утверждает,

что при

очень большом числе случайных явлений

средний

их

результат перестает

быть

случайным

может быть пред-

сказан

большой степенью

определенности.

Вот

примеры этого.

Пример

Тик,

хотя невозможно

предсказать,

какую конкретно сум-

му

снимет

или

положит

на

свой вклад очередной клиент Сбербанка, суммар-

ное

значение этих операций

за

день остается примерно одним

и тем же в

обычные

будничные

дни.

Пример

Суммарная продажа

,бензина

на АЗС

примерно одна

и та

же

обычные будничные

дни.

Пример

Крупный банк

ведет

множество

финансовых операций:

на

межбанковском рынке кредитует другие банки

и сам

занимает деньги,

принимает

выдает

вклады физических

лиц,

продает

покупает акции

облигации

т.п.

При

этом проигрыш

по

некоторым направлениям компен-

сируется

выигрышем

на

других,

что

обеспечивает банку устойчивое финан-

совое

положение.

Указанная

примере

стратегия работы банка соответствует

народной,мудрости:

«не

клади

все

яйца

одну корзину»

— и

пред-

ставляет,

по

сути

дела,

единственный разумный принцип работы

на

Финансовом

рынке. Научное название

этого

принципа

—

принцип

диверсификации

(переведем

как

принцип

«разнообразия»).

Он

озна-

чает,

что

нужно проводить разнообразные,

не

связанные друг

дру-

гом

операции,

тогда

убытки

от

одних операций будут более

или ме-

нее

покрыты прибылью

от

других операций.

271