Малыхин В.И. Математика в экономике

Подождите немного. Документ загружается.

Эта

производная обязательно

существует,

если

плотностьу(х)

не-

прерывна

этой

точке,

более

того,

производная

этом

случае

равна

f(x)

(см.

об

этом

п.

раздел

10.2).

Итак, справедливо такое

предло-

жение,

Предложен

ие 5. В

точках непрерывности плотности

произ-

водная

функции распределения равна плотности

этой

точке*

На

практике обычно плотности

— это

функции,

непрерывные

всюду,

кроме конечного числа

точек.

Следовательно, функция распределения

плотность

связаны

таким

предложением.

Предложение

б.

Чтобы найти

плотность,

надо

продиффе-

ренцировать

функцию

распределения:

Л*)

£"(*)'>

чтобы

найти

функ-

цию

распределения, надо проинтегрировать плотность;

F(x)

J/«d/.

—со

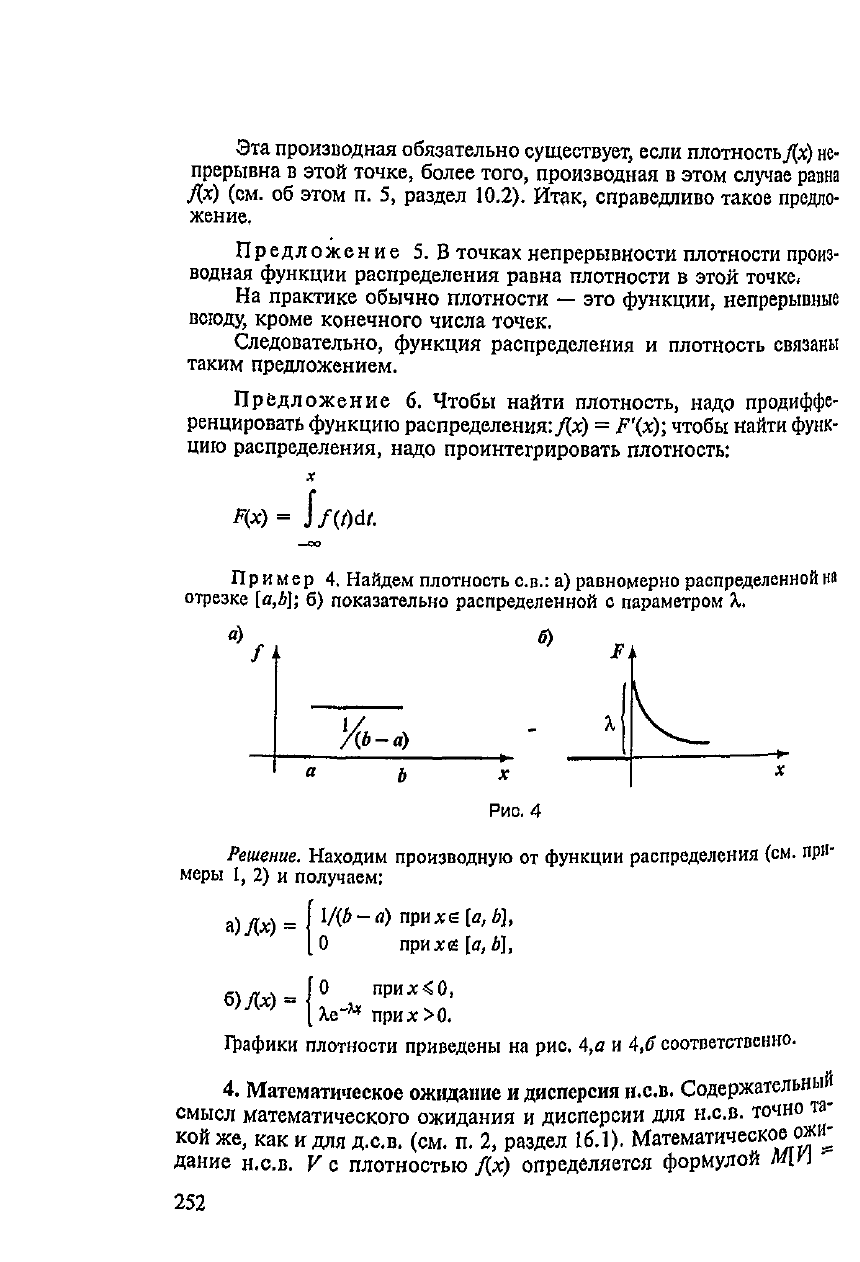
Пример

Найдем плотность

с.в.:

а)

равномерно

распределенной

на

отрезке

[а,Ь];

б)

показательно распределенной

параметром

Д..

Решение. Находим производную

от

функции распределения

(см.

при-

меры

1, 2) и

получаем:

)

уф

\/(Ь

«)

при

(а,

Ь],

[О

прияй

[а,Ь],

6>/fofta

J°

С)ЛЖ)

1?иГ*п

их>0.

Графики

плотности приведены

на

рис.

4,«

4,6

соответственно.

Математическое ожидание

дисперсия

н.с.в.

Содержательны^

смысл математического ожидания

дисперсии

для

и.с.в.

точно

та-

кой

же, как и для

д.с.в. (см.

п.

раздел 16.1). Математическое

ожи-

дание н.с.в.

Ус

плотностью

Л*)

определяется формулой

М[П

252

253

•ь»

=jxf(x)dx.

Дисперсия

же

определяется

точЪо

так же, как и для

д.с.в.,

—оо

т.е.

формулой

D[V\

Щ(У-

т)

]

ЩУ

]

т}.

Пример

Найдем

математическое ожидание

дисперсию

с.в.

а)

равномерно

распределенной

на

отрезке

[а,

Ь];

б)

показательно распреде-

ленной

параметром

(см. примеры

2, 4).

Решение,

M[V\

\x/(b

o)dx=

(a +

b)/2.

Теперь

вычислим

диспер-

сию.

М(У*]

)х

/(Ь

e)dx

\/(Ь

а)

•

д?/31

(и

)/(3(£

в))

аи

)/3,

/и

= (а +

/4.

Итак,

D[f^

(и

/12,

б)

A/[F]

JxXe"^dx,

Это

несобственный

интеграл, значит,

JxXe~

JxXe-'^dx.

Вычисляем интеграл

JxXe'^dx

по

частям, получаем

1Д)

1Д,

значит,

М{У]

1Д.

Примерно

так

же,

но

более длинно

сложно, вычисляется

диспер-

сия.

Приведем только результат

—

D[V\

1Д

Равномерное

распределение.

Систематизируем

информацию

об

этом

важнейшем

типе

н.с.в.

С.в.

Vравномерно

распределена

на

ыпрезке

[a,i],

если

ее

плотность веро-

ятности

постоянна

на

этом отрезке

равна

нулю

вне

его.

Ниже

приведены

Функции

плотности

Л*)

распреде-

ления

F(x)

вероятности,

графики

этих

функций

показаны

на

рис.

ЗД - (а

-Ь

А)Д

ЩУ\

(Ь

д)у12.

Рис-

Плотность

вероятности:

Д*)

{J/(A-e)

приле

[в,*],

[ 0

при

и,

Функция

распределения:

f(x)

(x-a)/(b-a)

приа<х<£,

ирнх>Ь.

Пример

б.

Цена деления шкалы прибора равна

0,5

атм.

При

снятии

"оказаний

оператор округляет

ближайшую сторону. Какова вероятность

того,

что

ошибка округления превысит 0,1?

Ответ.

3/5.

Пример

7. Он и Она

договорились встретиться

с 12 до 13

под

часа-

ми,

но

никто

не

смог

уточнить момент своего прихода. Однако

каждый

по-

обещал

ждать

другого

течение

минут. Какова вероятность

их

встречи?

Он

ждет

Ее уже

более

минут. Какова вероятность

того,

что в

оставшееся

время

Она еще

придет?

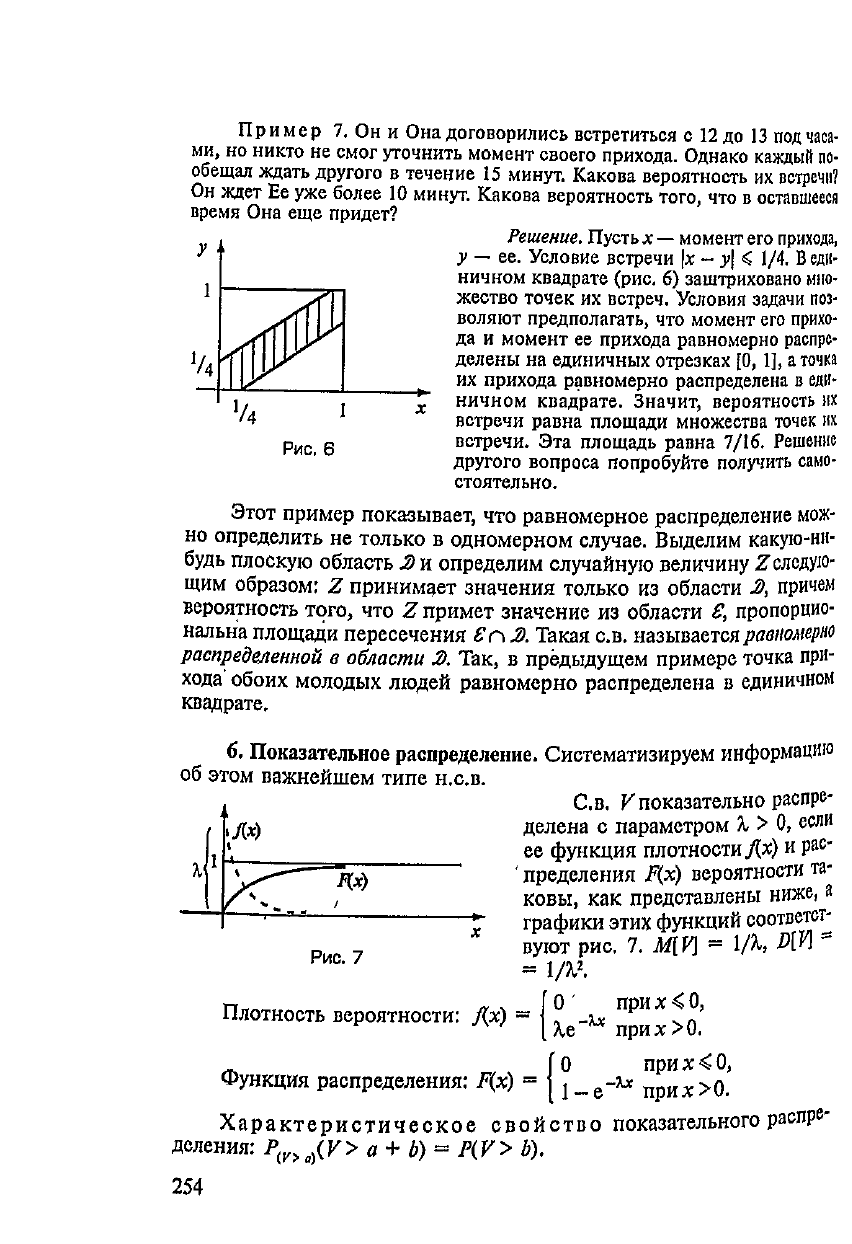
Решение.

Пусть

х—

момент

его

прихода,

у — ее.

Условие встречи

\х - у\

1/4,

еди-

ничном

квадрате

(рис,

заштриховано

мно-

жество точек

их

встреч.

Условия

задачи

поз-

воляют предполагать,

что

момент

его

прихо-

да и

момент

ее

прихода равномерно

распре-

делены

на

единичных отрезках

[0,1],

точка

их

прихода равномерно распределена

еди-

ничном

квадрате. Значит,

вероятность

их

встречи равна площади множества

точек

их

встречи.

Эта

площадь равна

7/16.

Решение

другого вопроса попробуйте

получить

само-

стоятельно.

Этот

пример показывает,

что

равномерное распределение

мож-

но

определить

не

только

одномерном случае. Выделим

какую-ни-

будь

плоскую область

2 и

определим случайную

величину

Zследую-

щим

образом:

принимает

значения только

из

области

причем

вероятность

того,

что Z

примет значение

из

области

€

пропорцио-

нальна

площади пересечения

£г\

Такая с.в.

называется

равномерно

распределенной

области

Так,

предыдущем примере

точка при-

хода'

обоих молодых

людей

равномерно распределена

единичном

квадрате,

Показательное распределение. Систематизируем

информацию

об

этом важнейшем типе

н.с.в.

С.в,

показательно

распре-

делена

параметром

Я-

> 0,

если

ее

функция

плотности

Л*)

ас

пределения

f(x)

вероятности

та-

ковы,

как

представлены

ниже,

графики

этих функций

соответст-

вуют рис,

M[V\

1А

КП*

1/Х

Плотность вероятности;

fix) - |

_iv

[Ке

прия>0.

при х

О,

Функция

распределения:

F(x)

j__

-**

рих>0.

Характеристическое

свойство

показательного

распре-

деления:

(v>a}

(V>

P(V>

b).

254

Доказательство,

По

определению условной вероятности имеем:

(vx,)(

(P((V>

+-b)

(V>

a))/P(Y>

а). Но (V> а +

Ь)п

(V>

а) = (У> а +

Ь),

значит,

P((V>

a +

(К>

а))

Р(К>

6).

Учтем,

что

Р(К>

с).

е~Ч

Окончательно получаем;

ДК>

а +

6)/Д

д)

е-

<°+

>/е-*

е~"

6),

что и

требовалось

до-

казать.

Пример

Утренняя

планерка

управлении

продолжается

среднем

около

часа.

На сей раз за час она не

закончилась.

Какова

вероятность

того,

что

она

продлится

еще не

меньше

мин?

Решение.

Пусть

V —

случайная

продолжительность

планерки. Есть

некоторые

основания

предполагать

ее

показательно

распределенной.

Возь-

мем

час за

единицу

времени,

тогда

(ибо

М[У]

1Д).

По

характерис-

тическому

свойству

показательного

распределения

имеем:

?,„>

..(V

> I +

1/4)

P(V> 1/4)

е~'/

0,8.

Показательное

распределение

простейший

по-

ток

событий. Пусть

0 —

последовательность событий, происхо-

дящих

случайные моменты времени. Например,

мы

наблюдаем зве-

здное

небо

с 0 ч до 3 ч

ночи

отмечаем моменты «падения

зцезд»

—

т-е.

сгорания

атмосфере сравнительно крупных метеоритов. Конеч-

но,

от

падения одного метеорита

до

падения следующего проходит

случайное

время. Предположим,

что эти

промежутки независимы

Друг

от

друга

показательно распределены

одним

и тем же

пара-

метром

(это соответствует действительности). Такой поток собы-

тий

называется

простейшим.

Оказывается,

что

число событий такого

потока,

происшедших

на

каком-то интервале времени, распределено

по

закону Пуассона

параметром, равным

Хг,

где t —

длина этого

промежутка

(о

законе Пуассона

см. п.

раздел

16.1).

Пример

9/Станция

«Скорой

помощи»

принимает

звонки

прось-

оой

медицинской

помощи.

Звонки

следуют

среднем

через

мин. Какова

вероятность

того,

что за

полчаса

будет:

а) 3

звонка;

б)

хотя

бы

один

звонок?

Решение.

Звонящие

на

станцию

действуют

независимо

друг

от

друга,

^то

некоторые

другие

соображения

дают

основания предполагать,

что

поток

звонков

—

простейший.

Значит,

число

звонков

за

какой-то

промежу-

ток

времени

распределено

по

закону

Пуассона:

Р(У~

К)

е~"

л*/Л1

нашем

примере

этот

промежуток

есть

полчаса,

следовательно,

есть

среднее

число

зйонков

за

полчаса,

т.е.

а - б.

Теперь

найдем

искомые

вероятности:

P(Y=

3) -

е-

/3!

1/11;

б)

Р(У>

0) = 1 -

Р(У~

1 -

е-

ЗАДАЧИ

С.в. распределена равномерно

на

некотором промежутке.

Найти

концы этого промежутка, если

ее

математическое ожидание

Равно

5, а

дисперсия равна 25/3.

255

Решение. Обозначим концы промежутка

а,

Ь,

тогда

имеем

систе-

му

уравнений:

1(£-й)

/12

25/3.

Решая

систему, получаем:

О,

= 10.

Манометр показывает давление

колонне,

которое

колеблет-

ся

от

10,0

до

10,2 атм,

и в

этих пределах любое давление

равновоэ-

можно.

манометр попал посторонний

предмет,

теперь

его

стрел-

ка

не

отклоняется больше

чем на

10,16

атм. Какое давление

сред-

нем

показывает манометр?

Клиент беспокоит

своего

брокера приказами

продаже

или

покупке

ценных бумаг. Поток таких приказов будем считать

простей-

шим,

среднем поступает один приказ

неделю. Последний

приказ

поступил

два дня

назад. Какова

вероятность,

что в

текущие

сутки

также

поступит приказ?

Указание.

Вспомните,

что

промежуток времени между

двумя

после-

довательными

событиями

простейшем потоке распределен

показательно;

воспользуйтесь

также характеристическим свойством

показательного

рас-

пределения.

16.4.

НАЧАЛЬНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ИНФОРМАЦИИ

Цель начальной статистической обработки

информации.

Пример

Отдел маркетинга крупной швейной фабрики

провел

ан-

кетирование

100

покупателей,

числе вопросов анкеты были

вопросы

пожеланиях

покупателей мужских костюмов.

Обработка анкет дала следующие результаты распределения

предпо-

чтений;

Оказалось,

что

ассортимент производства отличался

от

пожелали

покупателей. Отдел маркетинга представил дирекции фабрики

свои

предло-

жения

по

изменению ассортимента.

Пример

Отдел

маркетинга крупного

автозавода

провел

анкет

вание

владельцев автомобилей, купивших

5 лет

назад новые

автомооил

(посредниками

анкетировании были

дилеры-продавцы),

частности,

256

дел

интересовало,

сколько

километров

наездил

автрвладелец.

После

обра-

ботки

было

получено

следующее

распределение

(в

тыс,

км и в % от

числа

анкетируемых).

50-100

100-150

150-200

200-250

250-300

300

дирекции

автозавода

эти

данные

сочли

весьма

важными

— они

поз-

волили

значительно

уточнить

ресурс мотора

многих

деталей

выпускаемо-

го

автомобиля.

Напомним,

что

генеральная

совокупность

—

достаточно

большая

совокупность

более

или

менее однородных объектов, некоторая

ха-

рактеристика

которых меняется случайным образом

от

объекта

объекту.

Как

распределена

эта

характеристика

по

всей генеральной

совокупности

— в

этом цель изучения

этой

совокупности.

Если

бы

исследуемая

совокупность

была

маленькой,

то

можно было

бы

про-

сто

описать

ее

элементы

указанием характеристики каждого эле-

мента.

Но

генеральная совокупность слишком велика

(по

определе-

нию!).

Даже если возможно описать каждый

ее

элемент (современ-

ные

компьютеры вполне позволяют

это

сделать

по

крайней мере

по

многим

генеральным совокупностям), полученная информация была

бы

необозримой.

Человеческий

мозг

слабоват

для

анализа таких объ-

емов

информации.

Он

требует

обобщенной информации, представ-

ления

информации

компактной,

обозримой форме.

Цель

начальной

статистической

обработки

информации имен-

но

этом

(

—

представить

эту

информацию

компактной,

обозримой,

понятной

форме.

Так,

примерах

1, 2

информация

из

анкет была

подвергнута

аботке

итоге

представлена

компактной, обозри-

мой

форме.

свою

очередь,

как

полагал

обоих примерах отдел

'аркетинга,

массив

анкет адекватно отражал генеральную совокуп-

ность.

Интересно отметить,

что в

примере

генеральная совокуп-

но

"ъ

вгтолне

еа

льная,'

достаточно

четко

очерченная

совокуп-

ность.

примере

генеральная совокупность

— это

совокупность

всех

потенциальных покупателей продукции швейной фабрики,

ко-

°рая

не

является четко очерченной совокупностью.

Генеральная

совокупность

выборки

из

нее. Исследовать

вое

лементы

генеральной совокупности нецелесообразно

или

даже

не-

возможно

по

следующим причинам:

а)

генеральная совокупность

может

быть очень большой;

о)

изучение

даже

отдельного

элемента

может стоить большого

труда;

)

процессе изучения элементам может быть нанесен ущерб,

°гда

процессе

изучения

они

уничтожаются

т.д.

257

Поэтому

из

генеральной

совокупности

отбирают

несколько

эле-

ментов

и их

изучают.

Эти

несколько элементов

называются

выбор-

кой.

По

указанным выше причинам выборка

не

может быть

боль-

шой.

Однако

мы

хотим распространить выводы, сделанные

при

изу-

чении

выборки,

на всю

генеральную совокупность, т.е.

выборка

должна

быть представительной.

Другими

словами, выборка

должна

быть

моделью генеральной совокупности

точки зрения

интересую-

щих

нас

закономерностей. Стало быть, здесь

мы

имеем дело

общей

принципиальной проблемой любого моделирования

—

надо

найти

компромисс

между двумя противоречивыми требованиями;

для

уменьшения

трудоемкости исследования выборки

ее

хочется

сделать

поменьше,

но с

другой стороны

—

чтобы

она

была

представитель-

ной,

ее

надо

сделать

побольше.

Это

сложная проблема.

Методы

тео-

рии

вероятностей

математической статистики позволяют

частично

ее

решить. Подробнее

на

этом остановимся

дальнейшем.

Уточним

теперь

сам

предмет исследования генеральной

сово-

купности.

Для

применения количественных

методов,

частности

методов математической

статистики,

также методов

компьютерной

обработки,

будем

считать,

что

изучается некоторая

характеристика

элементов

генеральной

совокупности, имеющая числовую

оценку.

Как

примере

2 —

километраж,

пройденный автомобилем. Или,

как

примере

1 —

стоимость

костюма,

который предпочитает

купить

анкетируемый

покупатель.

Если

же

исследуемая

характеристика

не

имеет количественной

оценки,

то ее

легко закодировать,

придав

ее

оттенкам числовые коды. Например,

(нуль) будет

соответствовать

отечественным

костюмам,

а 1

(единица)

—

импортным (см.

пример

1J-

Подведем итог. Генеральная совокупность представляется

огром-

ной

необозримой совокупностью более

или

менее

однородных

объ-

ектов,

которых

нас

интересует некоторый количественный

при-

знак. Выборка

из нее —

сравнительно небольшой

ряд

этих

объектов,

которых сняты значения признака

— тем

самым получен

ряд

чисел.

Начальная

статистическая обработка

информации

свела

теперь

обработке этого сравнительно небольшого ряда

чисел.

Теперь,

после знакомства

со

случайными величинами,

можн

по-другому взглянуть

на

понятие генеральной совокупности.

Пр

положим,

что

исследуется с.в.

Значит,

мы

имеем

возможность

за

разом воспроизводить опыт,

результате которого

ини

КаК

какое-то значение.

Но

закон распределения

ЛГ

нам

неизвестен,

его

найти? Очевидно,

что нет

никакой иной возможности,

чем

лр

изводить

раз за

разом опыты, фиксировать

значения,

которые

нимает

X, и

пытаться

по

ряду этих значений определить

закон:

пределения

хотя

бы

приближенный.

Такой вопрос

уже

вот

перед нами, когда

мы по

частоте определяли

приближенно

в Р

ность

случайного события,

258

Представим

себе,

хотя

бы

мысленно,

совокупность всех значе-

ний,

которые может принять

с. в. X в

результате производимых опы-

тов.

Это и

есть исследуемая генеральная совокупность.

.Так

мы

свели

изучение

с.в.

изучению

соответствующей

генеральной совокупно-

сти

(всех

ее

потенциальных значений).

другой

стороны, пусть есть

какая-то

генеральная совокупность

и мы

интересуемся какой-нибудь

характеристикой

Y ее

элементов.

Исследование

отдельного

элемен-

та

генеральной совокупности можно считать проведением

опыта,

ходе

которого исследуемая характеристика

принимает какое-то

значение.

Так мы

свели изучение генеральной совокупности

изуче-

нию

соответствующей случайной величины (принимающей свои зна-

чения

на

элементах генеральной совокупности).

Итак,

определенном смысле случайная величина

генераль-

ная

совокупность

— это

одно

и то же.

Выборка

из

генеральной сово-

купности

серия опытов

со

с.в.

— эти

понятия,

определенном

смысле,

также можно

отождествить.

дальнейшем

мы

будем упо-

треблять

все

оти

понятия, руководствуясь соображениями удобства.

Характеристики

выборки. Обозначим исследуемую

с.в.

через

пусть

{<?,,

„

ф)

}

выборка,

в,,

...,

— ее

элементы,

—

объем

Статистическая обработка выборки начинается

составления

ряда

вариантов:

а)

элементы выборки

.,.,

располагают

порядке неубыва-

ния

получается

ранжированный

ряд

е,,

...,

е,;

б)

одинаковые

как

числа элементы выборки

группируют

вари-

Нт

*,,

...,

(таким образом,

v —

число

вариантов выборки).

Дальнейшая

обработка зависит

от

числа вариантов. Если

оно

иь/й

Т/°

Н6

Лее

то

составляют дискретный

вариациоп-

\гА

*•*

•

ДВР

составляют так;

подсчитываются частоты

/и,

частости

р,

/и/и,

....

вариантов

(очевидно,

что

J>,

!Д

1);

ся

ър

Строится

таблии

.акоторая

называет-

лин

^°

можно

пост

роить

многоугольник частостей

—

ломаную

«ию

на

плоскости, соединяющую точки

координатами

(

р).

По

ДВР

определяется также эмпирическая функция распределения

при

}

^(г)

р|+...

р,_,

прих,_,

<г<л

(/«2,.

.,у),

(О

при z >

259

Если

же

вариантов

много,

то

строится интервальный

вариацион-

ный

ряд

(ИВР):

назначаются

нижняя

граница

п'верхняя

граница

для

вари-

антов

так, чтобы отрезок

[а, Ь]

вместил

всю

выборку; часто

полагают

minx.,

Ь —

max*.,

но

иногда

a, b

назначают

из

соображений

удоб-

ства,

но не

слишком далеко

от

minx,

max*.;

' / '

находится

число

равных

по

длине интервалов

группирования,

которое

зависит

от

объема выборки

должно быть

не

меньше

8—10

и не

больше

20—25;

рассчитывается интервал группирования

(Ь~

*)/v;

устанавливается шкала интервалов

{

а,

...,

а,

А,

, -

—

отмечаются середины этих интервалов

...,

Л>

подсчитываются числа

/я,,...,

элементов выборки,

попав-

ших

каждый интервал;

эти

числа называются интервальными

час-

тотами,

интервальные

частости

р,

{

/п

(для этой цели

можно

использовать

ряд

вариантов

—

если

он

составлен),

при

подсчете

ча-

стот

интервал включают

его

левый конец

и не

включают

правый,

но

последний интервал правый конец также включают;

строится

таблица,

которая

и на-

зывается

ИВР.

Нужно

отметить, впрочем,

что

часто

ИВР

называют

только

по-

следние

две

строчки этой таблицы, т.е.

(2)

По

ИВР

можно построить

многоугольник

частостей

—

ломаную

линию

на

плоскости, соединяющую точки

координатами

(у,,

?)•

По

ИВР

определяется также эмпирическая функция

распреде-

ления

приг<я

*"*

/\.

-Ffe)-'

+,..+

/>ы

прид

;

<г<й

(/=2,...,v),

npHZ>fl

Нужно

отметить, впрочем,

что

эмпирическую

функцию

распре-

деления

определяют

и по

ряду

(2),

т.е.

точно

так,

как

(1):

пригар

^(г)=

/M+...+

/I/-I

при^,_,

<z<y,

(/«2

.»,v),

npuz>yv

260

Из

других характеристик выборки отметим среднее значение эле-

ментов

выборки,

или

просто среднее

значение

выборки,

или

выборочное

среднее:

(е

{

...

е1

)/п

(Ъе)/п,

/=i

или,

если составлен

ряд

вариантов

и их

частот,

(*,«,.+

... +

)/n

(£

xp)/n

/=i

или;

если составлен

ДВР,

*-*А+

... +

$,/>„-

£*,д.

/=i

Эти

два

последних способа дают точное значение выборочного

среднего.

случае составления

ИВР

по

нему можно найти приближен-

ное

значение выборочного среднего:

{

+ ... +

Д.

/=1

Аналогом дисперсии является выборочная

дисперсия:.

(i(e

-XW/n

(ie*)/n-X>,

/=i

/»i

или,

если составлен

ряд

вариантов

и их

частот,

*)Ч)/и

(£

й/

д:>)/л

Х\

/«1

/=1

или,

если составлен

ДВР,

•^

ЕЦ-^)

(1^)-^-

/=i

случае составления

ИВР по

нему можно

найтитфиближенное

зна-

чение

выборочной дисперсии:

(у,

(£

Д)

/=•!

/«1

ер

По

ез

льтатам

наблюдений:

I, 7,

7»

б,

3,4,

ник

ПОСТ

ОИТЬ

дискретный

вариационный

ряд,

многоуголь-

BUR

ЧаСТОСТей)

ик

выборочной

функции распределения. Подсчитать

ыоорочную

среднюю

выборочную дисперсию двумя способами.

Приду-

ать

правдоподобную генеральную совокупность

или

соответствующую

слу-

чайную

величину,

Решение.

Объем выборки

20.

Располагаем элементы выборки

в по-

Еш

возрастания:

^учили

ранжированный

ряд.

Теперь выделим варианты

и их

частоты

261