Максимов А.И., Мошников В.А., Таиров Ю.М., Шилова О.А Основы золь-гель-технологии нанокомпозитов

Подождите немного. Документ загружается.

своеобразного порогенного компонента. Порогенными компонентами в со-

временной науке называют вещества, исчезающие на различных стадиях

формирования и обработки материалов с образованием пор. Углеродные

материалы в процессе отжига в кислородсодержащей атмосфере превра-

щаются в газы. Возможность контролировать наноразмеры вводимых объ-

ектов из углеродных материалов предопределяет перспективность их ис-

пользования для получения структур с заданными размерами пор.

В научно-технической литературе для таких технологических методов

также используется термин "темплатный синтез", а вводимые частицы

темплатами или шаблонами(от template – шаблон). Новые материалы с уз-

ким распределением пор по размерам необходимы для создания полупро-

водниковых газочувствительных сенсорных устройств нового поколения,

композиционных мембран, хроматографических колонок и др.

Особо выделим роль пористых материалов, получаемых золь-гель ме-

тодом, при разработке технологических операций нанесения диэлектриче-

ских покрытий с низкими значениями относительной диэлектрической

проницаемости  в микро и наноэлектронике [

Это обусловлено тем, что уменьшение длины канала и МДП-

транзистора в целом на этапах миниатюризации микросхем позволяет по-

высить тактовую частоту процессоров и запоминающих устройств только

до определенного предела. С уменьшением расстояния между токопрово-

дящими элементами возрастает характеристическое время :

 = RC,

где R – сопротивление токопроводящих элементов, C – эффективная ем-

кость между проводящими элементами. Значения R и C возрастают при

уменьшении площади сечения проводника вдоль направления протекания

тока и уменьшении расстояния между проводящими элементами.

На современном этапе развития кремниевой наноэлектроники значе-

ние R стремятся снизить путем замены традиционного проводящего мате-

риала Al на Cu (или Cu в оболочке TiO

), а для снижения значения емкости

интенсивно развиваются исследования по материалам с низкими эффек-

тивными значениями относительной диэлектрической проницаемости 

(так называемые low-k dielectrics [

]). Одним из основных технологиче-

ских приемов снижения усредненного значения  является формирование

изолирующего слоя с нанопорами золь-гель методом.

Другим перспективным технологическим направлением является

формирование на пористой структуре системы каталитически активных

наночастиц. Использование таких подложек обеспечивает получение "на-

нотравы" (nanograss) из кремниевых или гетероструктурных нанопроводов

[

], [

], на основе которых изготавливаются приборы наноэлектроники,

нанооптоэлекроники [

], сенсорики [

] и фотоники на нанопроводах

[

]. К настоящему времени разработаны технологии получения гетерост-

руктурных нанопроволок (нанонитей) с изменением состава как вдоль оси

роста (аксиальные нанопроволочные гетероструктуры), так и в радиальном

направлении (радиальные нанопроволочные гетероструктуры). В обзоре

[52] обобщены данные о таких структурах на полупроводниковых соеди-

нениях A

, А

и твердых растворов на их основе. В качестве катализа-

тора, как правило, применяются наночастицы Au, а рост нанонитей проис-

ходит по механизму "пар-жидкость-кристалл".

Близкие по технологической схеме приемы используют при каталити-

ческом росте углеродных нанотрубок [

]. В качестве катализаторов чаще

всего используют Ni, Fe, Co и их сплавы и оксиды.

Научно-технические разработки устройств наноэлектроники и опто-

электроники, использующих углеродные нанотрубки обобщены в обзоре

[

Сначала 90-х гг. прошлого столетия, т.е. с момента разработки техно-

логии получения фуллеренов в макроколичествах, фуллерены и другие уг-

леродные материалы находятся в центре внимания многих исследователь-

ских групп. Опубликованы тысячи статей, десятки монографий и обзоров.

Особенно много публикаций посвящено фуллеренам. Фуллерены причис-

ляют одновременно как к неорганическим материалам в качестве новой

аллотропной модификации углерода, так и к объектам органической хи-

мии, поскольку в химических превращениях они проявляют свойства не-

предельных углеводородов [

]–[

]. Однако новые углеродные материалы

не ограничиваются фуллеренами.

Бурное развитие семейства углеродных материалов иллюстрируется

табл. 2.2, в которой приведена краткая историческая справка о хронологии

основных открытий в этой области, и выделяются некоторые свойства этих

материалов, привлекательные для использования в золь-гель технологии

нанокомпозитов.

Распространенная точка зрения, что до открытия фуллеренов сущест-

вовали только две полиморфные модификации углерода – алмаз и графит,

является сильно упрощенной.

Неправильным является и мнение о том, что фуллерены – первые мо-

лекулы с углеродной клеткой. Первые молекулы с замкнутым объемным

каркасом с формулой C

, названные адамантаном (трициклодеканом),

были синтезированы в 1933 году. Особо эстетически привлекательными

для химиков были задачи синтеза молекул с формами пяти правильных

(платоновых) тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра. (На-

помним, что у платоновых тел грани представляют собой правильные мно-

гоугольники: у куба – квадраты, у додекаэдра – пентагоны, у остальных тел

– равносторонние треугольники.)

Синтезированные молекулы вещества получали соответствующие на-

звания, например, кубан С

, додекаэдран С

и др. Большое количе-

ство углеводородов с полым углеродным каркасом, синтезированных к на-

стоящему времени, в англоязычной литературе имеет название "Cage

hydrocarbon molecules".

До открытия фуллеренов также были известны карбины (открыты в

СССР, акад. Коршак В.В. и сотр.). Карбины – это полимерная форма угле-

рода из линейных цепей [-СС-]

, где n > 10. В настоящее время известны

две полиморфные модификации карбинов. Карбины обнаружены в метео-

ритных углеродных включениях.

Процесс открытия новых углеродных материалов продолжается. На-

пример, в 2004 году группе исследователей (Новоселов и др., Великобри-

тания, Россия) удалось получить графен (лист графитовой плоскости тол-

щиной в 1 атом). Этот материал представляет большой интерес для нано-

электроники и спинтроники.

Сведения, приведенные в табл. 2.2., не претендуют на полноту рас-

смотрения бурно развивающегося материаловедческого направления на

основе углеродных материалов.

Таблица 2.1

Хронология открытий в области новых углеродных материалов и наноструктур

год

Характерные особенности углеродных материалов

1963

Синтез наноалмазов из углерода взрывчатых веществ (К.В. Волков,

В.В. Даниленко, В.Н. Блик – СССР)

1973

Теоретическое предсказание устойчивой молекулярной структуры С

(фуллерена) – Д.А. Бочвар, Е.Г. Гальперн – СССР

1980

Экспериментальное наблюдение полых замкнутых многослойных уг-

леродных кластеров (С.Иджима – Япония)

1985

Открытие фуллеренов С

и С

(Ш.Крото, Р.Курл, Р.Смолли – США,

Великобритания). Нобелевская премия 1996 г.

1987

Экспериментальное наблюдение углеродных "луковичных" структур

(С. Иджима – Япония)

1990

Разработка способа массового синтеза фуллеренов дуговым методом

(В.Краецчмер, Д. Хаффман – США, Германия)

1991

Открытие углеродных нанотрубок (С.Иджима – Япония)

1991

Интеркалированные соединения M

(M = Rb, Cs, Na, K…; n = 0…6)

Сверхпроводимость в M

Синтез фуллеренов методом сжигания углеводородов

Синтез эндоэдральных фуллеренов M@C

, M@C

и др.

1992

Синтез углеродных нанолуковиц под воздействием электронного пучка

1993

Синтез полимеров на основе фуллеренов

1994

Разработка методов получения эндоэдральных углеродных нанотрубок.

Сверхпроводимость в эндоэдральных нанотрубках TaC@C

1998

Синтез углеродных наностручков

1998 –

по настоящее

время

Разработка разнообразных методов химической модификации фулле-

ренов: присоединение функциональных групп по двойным связям (эк-

зопроизводные), введение атомов и кластеров внутрь углеродной сфе-

ры фуллеренов и углеродных нанотрубок (эндопроизводные). Получе-

ние графена. Образование новых соединений замещением атомов угле-

рода атомов углерода атомами других химических элементов (гетеро-

фуллерены). Создание МДП-транзисторов на углеродных нанотрубках

(УНТ). Основы создания углеродной наноэлектроники. Суперконден-

саторы на базе углеродных материалов

Углеродные наноматериалы представляют большой интерес для раз-

вития технических направлений микро- и наноэлектроники, спинтроники,

новых информационных устройств (особенно на основе эндоэдральных

структур), суперконденсаторов, топливных элементов для водородной

энергетики. Сочетание с процессами золь-гель технологии может привести

к созданию принципиально новых устройств нового поколения. При этом

следует выделить три основных применения:

1 – использование углеродных наноматериалов как наполнителей (см.

схему рис. 2.4) в золь-гель процессах для синтеза гибридных нанокомпози-

тов,

2 – использование углеродных наноматериалов как порогенов для

формирования пористых структур с калиброванными размерами пор,

3 – применение золь-гель технологии для получения подложек с ката-

литически активными наночастицами для управляемого получения нано-

систем из углеродных нанотрубок.

Ограничимся рассмотрением наиболее важных свойств углеродных

материалов (табл. 2.2), обусловленных внутренним расположением атомов

углерода и предопределяющих возможность формирования нанокомпозита.

К моменту открытия фуллеренов в науке уже сформировалось новое

направление, изучающее физику и химию кластеров. Термин "кластер" (от

англ. сluster – "гроздь", "рой") был введен в науку в 60-х годах 20-го века

Ф.А.Коттоном [39]: "Кластеры – полиэдрические группы из атомов металла

– можно определить как группы, содержащие конечное число атомов ме-

талла, которые удерживаются полностью , в основном, или хотя бы в зна-

чительной степени связями, образованными непосредственно между ато-

мами металла, хотя с такими кластерами могут быть связаны и некоторые

атомы неметаллов". Экспериментально (методом масс-спектрометрии) бы-

ло установлено, что для кластеров различных металлов характерны неко-

торые определенные количества атомов в кластере, при которых кластер

является относительно устойчивым (эти значения получили название "ма-

гических чисел"). Следует отметить, что типичные значения числа атомов

в устойчивых кластерах находятся в "мертвой зоне" для существующих

теоретических представлений. Для методов квантовой химии задача стано-

вится "слишком многочастичной", в то время как модели, основанные на

представлениях "зонной теории", начинают работать только когда количе-

ство атомов в кластере N становится больше 10

(другими словами, когда

появляется упорядоченный потенциальный рельеф на поверхности час-

тиц).

Наиболее плодотворными моделями предсказания "магических чисел"

являлись модели, основанные на удовлетворении полноты заполнения

обобщенных электронных оболочек (особенно для щелочных металлов) и

геометрические модели в рамках приближения жестких сфер. Последние

модели обеспечивали не только объяснение конкретных значений "магиче-

ских чисел", но и предсказывали геометрическую форму кластеров. Экспе-

риментальные данные электронной микроскопии ограненных кластеров

Pd, содержащих 561 атом (Pd

561

), подтвердили правильность развиваемых

моделей.

Основные принципы геометрической организации кластеров сводятся

к следующим [39]:

1. наиболее устойчивыми являются структуры кластеров, имеющих

максимальное число связей, приходящихся на один атом;

2. кластеры стремятся к квазисферической форме;

3. кластеры с более высокой симметрией предпочтительнее.

Другими словами принципы геометрической организации кластеров

построены на базе минимизации свободной энергии. (Максимальное число

связей минимизирует энергию связи. Кластеры стремятся образовать плот-

ные структуры с минимальной поверхностной энергией. Одинаковые ато-

мы, слагающие каркас кластера, должны пребывать в неотличном друг от

друга положении и состоянии.) Из этого вытекает, что оптимальной фор-

мой устойчивых кластеров в трехмерном пространстве будут являться ко-

ординационные многогранники с геометрически эквивалентными верши-

нами. Числа атомов, заполняющих эти многогранники, и образуют набор

"магических чисел". В частности, проводя усечение октаэдров с различным

количеством атомов на ребре до образования кубооктаэдра, можно легко

получить набор "магических чисел" (1; 13; 55; 147; 309; 561; 923…), часто

наблюдающихся в экспериментах. Как отмечалось выше, кластер Pd

561

(11

атомов в "базовом" октаэдре) удается наблюдать методом электронной

микроскопии.

В кластерах часто устойчивыми являются формы с осью симметрии 5-

го порядка (формы на базе икосаэдра и пентагональной бипирамиды).

У некоторых обучающихся это вызывает недоумение. Из курсов кри-

сталлохимии, кристаллофизики или теории групп они аксиоматично ус-

воили, что в кристаллах разрешены оси симметрии только 1-го, 2-го, 3-го,

4-го и 6-го порядков. Для исключения недоразумений отметим, что запрет

на оси 5-го порядка получен в исходном предположении бесконечного кри-

сталла. В наномире нет запрета на ось 5-го порядка.

Приведенные сведения по строению кластеров мы будем использовать

в п.2.8 при рассмотрении современных представлений о гетерокатализе на

наночастицах. Здесь же остановимся на экспериментальных результатах,

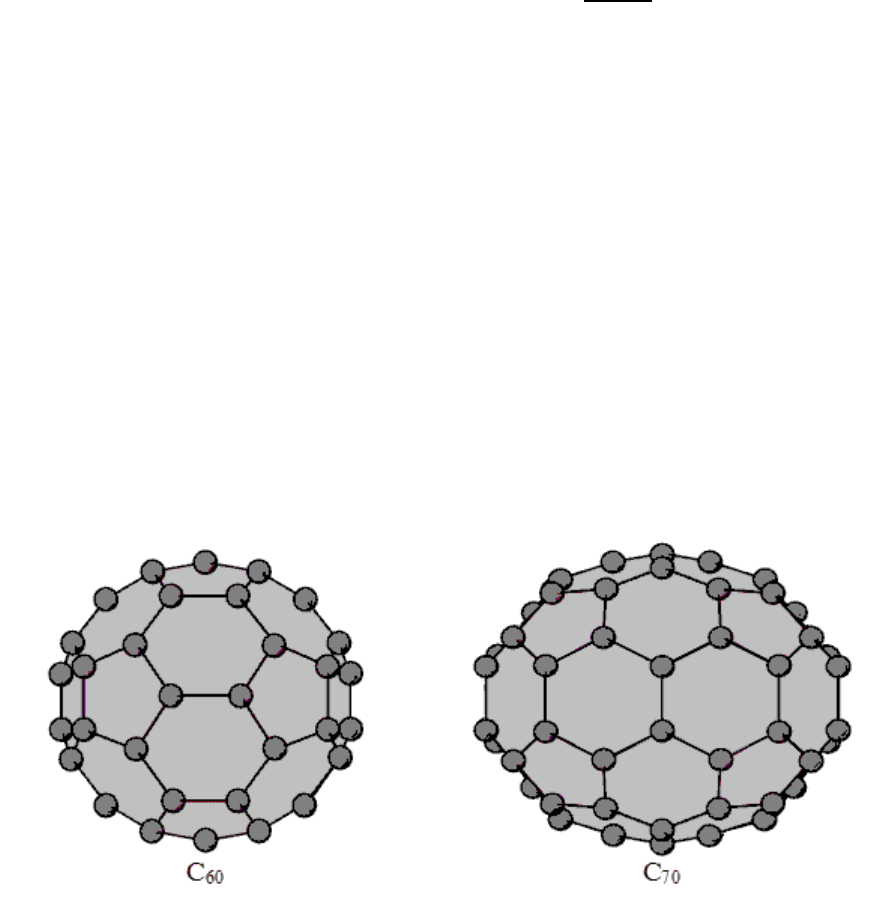
приведших к открытию фуллеренов и отмеченных Нобелевской премией.

Из данных по масс-спектрометрии следовало, что наиболее устойчивыми

углеродными кластерами являются C

и C

. Эти значения N, равные 60 и

70, не описывались сложившимися представлениями на основе геометри-

ческой организации кластеров.

В результате была предложена не плотная, а полая модель образования

структуры C

. Это фактически модель нового ранее неизвестного молеку-

лярного строения шестидесяти атомов углерода. 60 атомов углерода орга-

низуются в форме усеченного икосаэдра. Если описывать строение C

многогранником, то атомы расположены в вершинах пересечения пентаго-

нов и гексагонов. 20 гексагонов (от двадцати исходных треугольников ико-

саэдра) и 12 пентагонов (результат сечения икосаэдра). Такая форма строе-

ния характерна для футбольного мяча и используется в архитектуре и

строительстве. В честь ученого Ричарда Бакмистера Фуллера, ранее пред-

ложившего эти формы в архитектуре, и возникло название новых углерод-

ных материалов – "фуллерены". В структуре фуллерена C

на каждый

атом приходится 4 связи (рис. 2.7) – 2 одинарных и 1 двойная (условие бли-

зости к полной валентности). Из-за наличия двойных связей сферическая

форма фуллерена C

слегка искажена.

Рис. 2.7. Строение молекул фуллеренов.

Строение фуллеренов C

, C

и высших фуллеренов C

(n  72) легко

представить, используя известные теоремы Л. Эйлера для полуправильных

многогранников вписанных в сферу или сфероид. Из первой теоремы:

 N

(6 – n) = 12s,

где n – индекс многоугольника, N

– количество многоугольников с n вер-

шинами, s – индекс, описывающий кривизну пространства (s = 0 для плос-

кости, s = 1 для сферы или сфероида), следует, что для многогранника со-

держащего гексагоны и пентагоны, количество пентагонов N

всегда равно

12. Из теоремы не следует ограничений на количество гексагонов N

Вторая теорема связывает число вершин В, граней Г и ребер Р для та-

ких структур:

В + Г – Р = 2.

Так как из каждой вершины исходит по 3 ребра и каждое ребро при-

надлежит 2 граням, количество ребер равно:

Р = 3В/2.

В качестве примера определим Г, Р, N

для фуллерена C

Так как количество атомов углерода В равно 70 и количество пентаго-

нов N

равно 12, то:

Р = 3В/2 = 105, Г = Р – В + 2 = 37 и N

= Г – N

= 25.

Из упрощенной схемы образования фуллеренов из графеновых плос-

костей (с sp

-гибридизацией электронных оболочек атомов углерода) выте-

кает, что наименьшие механические искажения (минимальная энергия)

возникают при наименьшем отличии числа вершин в индивидуальном мно-

гоугольнике от 6. То есть выпуклые углеродные многогранники должны

состоять из гексагонов и пентагонов. Кроме того, механические искажения

должны как можно однороднее распределяться по структуре. На этом ос-

новано правило изолированных пентагонов (правило IPR – Isolated

Pentagon Rule). Для фуллерена C

это правило приводит к тому, что каж-

дый пентагон соприкасается только с гексагонами, а стороны каждого гек-

сагона поочередно с пентагонами и гексагонами.

Используя правило IPR, можно показать, что структура C

содержит

единственный изомер, а также, что следующим фуллереном, отвечающим

требованиям IPR и симметрии является C

. Однако для высших фуллере-

нов задача становится менее определенной. Например, для достаточно рас-

пространенного фуллерена C

общее количество изомеров достигает уже

51592. Из них 24 отвечают правилу IPR (экспериментально выделено 2 ос-

новных и 6 примесных изомеров [55]).

Для анализа изомеров весьма полезным является использование топо-

логических диаграмм Шлегеля, сущность которых заключается в проекти-

ровании всех вершин на одну из граней, выделенную в качестве базисной.

На рис. 2.8 в качестве примера приведена диаграмма Шлегеля для фулле-

рена C

Рис. 2.8. Диаграмма Шлегеля для фуллерена C

Наличие двойных связей представляет возможность получения широ-

кого класса экзопроизводных соединений. Для топливных элементов водо-

родной энергетики важной характеристикой является возможность связы-

вания атомов водорода. На основе C

можно получать разнообразные мае-

риалы C

, где n в теоретическом пределе может достигать 60. (Экспе-

риментально получение больших значений n затруднительно. Здесь для нас

важно понимать, что свойства материалов C

с разным n отличаются

друг от друга. Более того, свойства материалов с одним и тем же числом n

зависят от того, какие двойные связи разорваны). Соединения на основе

фуллеренов называют фуллеридами.

Двойные связи являются основой образования полимерных модифи-

каций фуллеренов. На рис. 2.9 приведены 3 существующие полимерные

модификации на базе фуллеренов.

Рис. 2.9. Полимерные модификации материалов на базе фуллеренов.

Разорванные двойные связи являются основой и для формирования

нанокомпозитов, они необходимы для образования химических связей с

атомами матрицы.

В 1991 году было получено кристаллическое состояние для фуллере-

нов C

, а затем C

. Кристаллы на основе фуллеренов получили название

– "фуллериты". Кристаллическая структура соответствует гранецентриро-

ванной кубической решетке (ГЦК-фаза). До сих пор не получены образцы

со 100% ГЦК-фазой. Как правило, образцы характеризуют как смесь ГЦК-

и ОЦК-фаз (ОЦК – объемно-центрированная кубическая решетка). сущест-

вуют модельные представления, предполагающие принципиальную невоз-

можность получения "чистой" ГЦК-фазы. Не вдаваясь в глубокое рассмот-

рение этих теоретических взглядов, отметим, что они имеют веские осно-

вания. Кристаллическая фаза (фуллерит) образована не из атомов, а из "мо-

лекул" C

. Основными силами взаимодействия являются ван-дер-

ваальсовы силы, соответственно существует определенная постоянно ме-

няющаяся динамическая составляющая, обусловленная поляризацией. Это

весьма близко представлениям о динамическом поляризационном кластере.

Для технических применений фуллериты сразу же привлекли внима-

ние как перспективные материалы для криоэлектроники. На базе их полу-

чены новые интеркаляционные соединения. Интеркаляционные материалы

ранее развивались путем введения чужеродных атомов в слоистые струк-

туры. Физическая сущность интеркаляции заключается в том, чтобы вве-

сти, например, ионы щелочных металлов малого радиуса под действием

электрического поля между слоями исходной матрицы. После выключения