Макконнелл К.Р., Брю С.Л. Экономикс: принципы, проблемы и политика

Подождите немного. Документ загружается.

ГЛАВА 27

601

у;

-I

• Ресурс будет употребляться в таком количест-

ве, при котором прибыль максимальна, то есть когда

предельная прибыль от производства равняется пре-

дельным издержкам на ресурс

(MRP

MRC).

• Применение правила MRP =

MRC

к кривой MRP

фирмы показывает, что кривая MRP - это кривая

спроса фирмы на ресурс.

• Кривая спроса на ресурс совершенно конку-

рентного продавца снижается только потому, что пре-

дельная продукция ресурса уменьшается; кривая

спроса на ресурс несовершенно конкурентного про-

давца снижается, потому что предельная продукция

и цена продукции уменьшаются по мере увеличения

объема производства.

ФАКТОРЫ

СПРОСА НА РЕСУРСЫ

Что приведет к изменению спроса на какой-либо

ресурс, то есть к сдвигу кривой спроса? Само пост-

роение кривой спроса на ресурс основывается на

двух взаимосвязанных факторах - эффективности

использования (производительности) ресурса и

рыночной цене продукта, который производится из

данного ресурса. В приведенном ранее анализе из-

менения спроса на

продукт(см.гл.

3)вводится

еще

один фактор - изменение цен на другие ресурсы.

Изменения спроса на продукт

Поскольку спрос на ресурс является величиной

производной, то неудивительно, что любое измене-

ние спроса на продукт будет влиять на цену про-

дукта и, следовательно, на MRP данного ресурса.

Отсюда вывод: при прочих равных условиях изменение

спроса на продукт, который производится определен-

ным видом труда, приведет к сдвигу спроса на труд в

том же самом направлении.

Так, в табл. 27-1 мы предположили, что повы-

шение спроса на продукт привело к повышению

цены продукта — с 2 до 3 дол. Если вы вычислите

значения новой кривой спроса на труд и нанесете

их на рис. 27-1, то увидите, что эта кривая располо-

жена справа от первоначальной. Аналогичным об-

разом падение спроса на продукт и снижение его

цены повлечет сдвиг кривой спроса на труд влево.

Изменения производительности

При неизменности других факторов изменение про-

изводительности труда ведет к изменению кривой

спроса на труд в том же направлении. Например,

Производство и спрос на ресурсы

если мы удвоим значение

МРв

столбце (3) табл. 27-1.

то обнаружим, что показатели MRP тоже удвоятся,

что означает рост спроса на труд.

На производительность (эффективность исполь-

зования) любого ресурса можно влиять различны-

ми путями.

1. Нетрудовые затраты. Данные о предельной про-

изводительности, скажем, труда будут зависеть от

количества других связанных с ним ресурсов. Чем

больше величина таких связанных с трудом ресур-

сов, как капитал и земля, тем выше будут предель-

ная производительность и спрос на труд.

2. Технический прогресс. Технологические усовер-

шенствования вызывают те же самые последствия.

Чем выше уровень технологии, тем выше произво-

дительность труда. Труд сталелитейщиков, работа-

ющих на современных кислородных конвертерах,

является более производительным, чем труд заня-

тых на старых мартеновских печах, в которые вло-

жено такое же количество реального капитала.

3. Повышение качества труда. Усовершенствование

самого переменного ресурса — труда — влечет за

собой повышение предельной производительности

и, следовательно, спроса на труд. В результате по-

лучаем новую кривую спроса на другой, более ква-

лифицированный, вид труда.

Все эти соображения важны для объяснения

того, почему средний уровень реальной заработной

платы в Соединенных Штатах Америки

выше,

чем

в большинстве зарубежных стран. Американские

работники в целом здоровее и лучше подготовле-

ны, чем работники в других странах, и в большин-

стве отраслей они трудятся с использованием более

крупного и более эффективного парка средств про-

изводства, а также богатых природных ресурсов. Это

создает устойчиво высокий спрос на труд. Со сто-

роны предложения труд является относительно ред-

ким ресурсом на рынке США по сравнению с боль-

шинством зарубежных стран. Устойчивый спрос и

относительно ограниченное предложение порожда-

ют высокие ставки заработной платы. Об этом пой-

дет речь позже, в главе 28.

Цены на другие ресурсы

Точно так же, как изменения цен на другие продук-

ты вызывают изменение спроса на какой-то опре-

деленный товар, изменения цен на другие ресурсы

могут повлиять на спрос на конкретный ресурс

Характер зависимости спроса на продукт

от изме-

нения цены продукта

Xопределяется

тем, являются

ли X и Y замещающими или дополняющими друг

друга товарами (см. гл. 3). Аналогичным образом

воздействие изменений цены ресурса

на спрос на

ресурс

будет зависеть от того, взаимозаменяемые

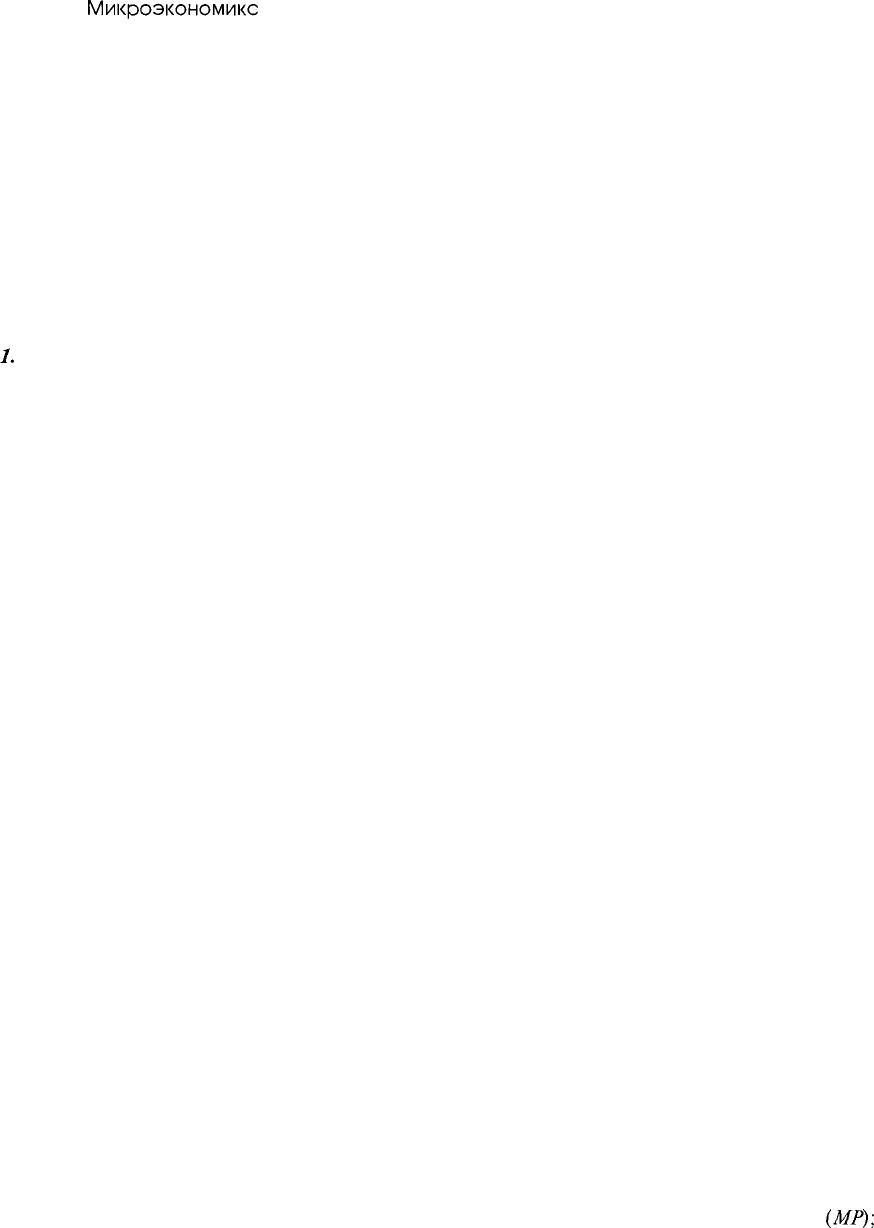
602

ЧАСТЬ ШЕСТАЯ

Микроэкономике

рынков ресурсов

это продукты или они в известной степени допол-

няют друг друга.

Замещающие ресурсы. Предположим, что в некото-

ром производственном процессе применяется такая

технология, что труд и капитал замещают друг дру-

га. Другими словами, фирма может производить

какую-то продукцию при относительно небольшом

количестве труда и относительно большом количе-

стве капитала, и наоборот. Теперь допустим, что

происходит падение цены на машины и оборудова-

ние. Соответствующее изменение спроса на труд

будет результатом двух противоположных тенден-

ций: эффекта замещения и эффекта объема произ-

водства.

Эффект замещения. Во-первых, снижение цен

на машины и оборудование побуждает фирму за-

мещать труд машинами и оборудованием. Это —

явно приспособительная реакция, поскольку фир-

ма стремится произвести любое заданное количе-

ство продукции с наименьшими затратами. При

данных ставках заработной платы в этом случае

будет привлечено меньшее количество труда. Ко-

роче говоря, эффект замещения снизит спрос на

труд.

2. Эффект объема производства. Во-вторых, при

падении цен на машины и оборудование также сни-

жаются издержки производства различных объемов

продукции. При сокращении издержек фирме вы-

годнее производить и реализовывать больший объ-

ем продукции. Увеличение объема производства

приведет к росту спроса на все ресурсы, включая

труд. В связи со снижением цены на машины и обо-

рудование эффект объема производства повлечет за

собой рост спроса на труд.

Повторим: эффект замещения показывает, что

фирма приобретет больше того сырья, относитель-

ная цена которого упала, и, наоборот, использует

меньше того сырья, относительная цена которого

возросла. Таким образом, снижение цены капитала

увеличит относительную стоимость труда и, следо-

вательно, уменьшит спрос на него. Иными слова-

ми, возникает эффект объема производства, так как

изменение цены ресурсов повлияет на издержки и,

следовательно, повлечет за собой рост объемов

прдукции, максимизирующий прибыль. Снижение

цены капитала снизит производственные издерж-

ки, увеличит объем продукции, максимизирующий

прибыль, и повысит спрос на труд.

Эффекты замещения и объема производства

явно действуют в противоположных направлени-

ях. При падении цен на машины и оборудование

эффект замещения снижает, а эффект объема про-

изводства увеличивает спрос на труд. Фактически

воздействие на спрос на труд будет зависеть от

соотношения этих двух противоположных тенден-

ций. Если эффект замещения перевешивает эффект

объема производства, то снижение цен на капитал

приведет к снижению спроса на труд. Если спра-

ведливо обратное, то спрос на труд увеличится.

Если эффект замещения перевешивает эффект объ-

ема производства, то изменение цены замещающего

ресурса вызывает такое же изменение спроса на

труд. Если эффект объема производства превышает

эффект замещения, то изменение цены замещающе-

го ресурса вызывает противоположное изменение

спроса на труд.

Дополняющие ресурсы. Вспомним из главы 3, что

определенные продукты, такие, как камеры и плен-

ки, компьютеры и программное обеспечение, на-

зываются дополняющими товарами в том смысле,

что спрос на них предъявляется одновременно.

Ресурсы могут быть взаимодополняющими в том

смысле, что увеличение количества одного из них

в некотором производственном процессе повлечет

за собой такое же увеличение количества другого

ресурса, и наоборот. Предположим, что мелкий

производитель металлоизделий использует штам-

повочные прессы в качестве главного элемента ос-

новного капитала. Каждый пресс сконструирован

так, что им может управлять один рабочий; пресс

не автоматизирован — он не будет работать сам по

себе, — и вместе с тем второй рабочий будет не

нужен.

Предположим, что значительные технологичес-

кие нововведения в производстве этих прессов при-

вели к существенному снижению их стоимости.

Теперь не будет никакого негативного эффекта за-

мещения, ибо труд и капитал должны применяться

в фиксированных пропорциях — один человек на один

пресс. Капитал теперь нельзя замещать трудом. Но

в отношении труда действует позитивный эффект

объема производства. При прочих равных условиях

снижение цен на средства производства означает

сокращение объема продукции. Соответственно ста-

нет выгодно производить больше продукции. По-

ступая так, фирма будет использовать одновремен-

но и больше капитала, и больше труда. Если труд и

капитал являются взаимодополняющими фактора-

ми, то снижение цены на машины и оборудование

приведет к повышению спроса на труд в силу эф-

фекта объема производства. И наоборот, при повы-

шении цены элементов капитала эффект объема

производства вызовет сокращение спроса на труд.

Следовательно: изменение цены взаимодополняющего

ресурса приводит к разнонаправленному изменению

спроса на труд.

Суммируем наши рассуждения: кривая спроса на

труд повышается (сдвигается вправо), когда:

1) увеличивается спрос (соответственно и цена)

на продукт, производимый этим трудом;

2) растет производительность труда

(МР);

3) снижается цена на замещающий ресурс при

условии, что эффект объема производства сильнее

эффекта замещения;

4) растет цена замещающего ресурса при усло-

вии, что эффект замещения превышает эффект объ-

ема производства;

5) снижается цена на дополняющий ресурс.

Убедитесь в том, что вы можете «перевернуть»

эти обобщения и объяснить, что будет в результате

снижения спроса на труд.

Примеры из реальной практики

Показатели спроса на труд имеют большое практи-

ческое значение. Насколько они важны, видно из

следующих примеров.

1. Рабочие американской автомобильной промышлен-

ности,

1995 г. в американской автомобильной

промышленности было занято на 400 тыс. рабочих

меньше, чем в 1979 г. Два фактора помогают объяс-

нить столь резкое сокращение числа рабочих мест.

Во-первых, иностранная конкуренция, особенно со

стороны японских производителей, сократила спрос

на американские автомобили. Доля американского

рынка автомобилей, занимаемого американскими

фирмами, упала с 80% в 1979 г. почти до 66% в 1995 г.

Снижение спроса на американские автомобили рез-

ко сократило вторичный спрос на американских

рабочих, занятых в автомобильной промышленнос-

ти. Вторым фактором стало распространение авто-

матизированных технологий в производстве авто-

мобилей. Рабочие на конвейере были заменены про-

мышленными роботами, что еще дополнительно со-

кратило спрос на рабочих автомобильной промыш-

ленности.

2. Работники ресторанов быстрого обслуживания. За

последние несколько лет компания McDonald's и

другие компании, содержащие рестораны быстрого

обслуживания, дали многочисленные рекламные

объявления с целью привлечения домохозяек и по-

жилых людей на работу. Основная причина этого

состоит в том, что все больше женщин работают вне

дома, и их семьи должны питаться в ресторане, а не

дома. Повышение спроса на ресторанное обслужи-

вание увеличило спрос на работников в ресторанах

быстрого обслуживания. Так как предложение тру-

да со стороны традиционных работников таких ре-

сторанов — подростков — отставало от спроса, то

многие рестораны стали привлекать на работу до-

мохозяек и пенсионеров.

3. Персональные компьютеры. За последнее деся-

тилетие произошло резкое снижение средней цены

персонального компьютера и не менее внушитель-

ное увеличение мощности типичного компьютера.

ГЛАВА 27

Производство и спрос на ресурсы

Влияние этих факторов на спрос на труд было од-

новременно положительным и отрицательным.

Между

1975

и 1990 гг. занятость в отрасли компью-

терных услуг (программное обеспечение) ежегод-

но росла на 12%. В некоторых офисах компьютеры

и рабочая сила (операторы) были дополнительны-

ми ресурсами. Поэтому снижение цен на компью-

теры сократило производственные издержки в та-

кой степени, что цены на товар или услугу снизи-

лись, продажи возросли и вторичный спрос на опе-

раторов также вырос. В противоположность этому

в других офисах компьютеры заменили рабочую

силу, сократив спрос и позволив этим фирмам ис-

пользовать меньше работников для производства

своих товаров и услуг. Пример: в конце 1993 г.

Налоговое управление США объявило, что усовер-

шенствование его компьютерной системы позво-

лит на

'/з

сократить число работников, необходи-

мых для обработки налоговых деклараций и дру-

гой работы, осуществляемой вручную.

4. Сокращение оборонной промышленности. Оконча-

ние «холодной войны» и последовавшее затем со-

кращение расходов на оборону резко снизило спрос

на труд со стороны военных производств и ведомств.

По некоторым оценкам, между 1993 и 1998 г. число

соответствующих рабочих мест сократилось на

800 тыс. - до 1 млн. Снижение федеральных расхо-

дов на оборону также значительно сократит спрос

на труд в отраслях, производящих самолеты, снаря-

ды, танки и другое военное оборудование. По оцен-

кам, между 1993 и 1998 г. сокращено около 1 млн

гражданских рабочих мест, так или иначе связан-

ных с оборонным производством.

5. Временные рабочие. Одно из основных измене-

ний на рынке труда за последние годы состоит в

том, что многие наниматели сократили число ос-

новных постоянно занятых работников и одновре-

менно увеличили число временных работников. По-

чему увеличился спрос на временную рабочую силу?

Во-первых, еще более дорогими стали социальные

пособия — страхование здоровья, выплаты в пенси-

онный фонд, оплаченные отпуска и оплата по бо-

лезни; обычно такие социальные пособия времен-

ным работникам не предоставляются, что обеспе-

чивает снижение издержек. Во-вторых, временные

работники позволяют фирме проявлять больше гиб-

кости при изменении экономических условий. Ког-

да изменяется спрос на продукцию, фирма может

быстро увеличить или уменьшить количество рабо-

чей силы, изменяя число временных рабочих. Эта

гибкость улучшает конкурентные позиции фирмы

и часто повышает ее конкурентоспособность на

международных рынках.

В табл. 27-3 приводятся дополнительные сведе-

ния о факторах спроса на труд.

604

ЧАСТЬ ШЕСТАЯ

Микроэкономике

рынков ресурсов

Таблица 27-3.

факторы

спроса на труд, смещающие кривую

спроса

1. Изменения спроса на продукцию. Примеры: растет по-

пулярность компьютерных программ, что увеличивает спрос на

работников фирм, производящих программное обеспечение;

потребители предъявляют повышенный спрос на кожаные паль-

то, следовательно, повышается спрос на дубильщиков кожи.

Изменения производительности. Примеры: повышение

квалификации стеклодувов увеличивает спрос

иа

их услуги; ком-

пьютерный графический дизайн увеличивает производитель-

ность труда и спрос на дизайнеров.

3. Изменения цен на другие ресурсы. Примеры: повыше-

ние цены

злектрознергии

увеличивает затраты на производст-

во алюминия и сокращает спрос на рабочих алюминиевой про-

мышленности, цена охранного оборудования, используемого

фирмами для защиты от несанкционированного входа, падает,

что вызывает снижение спроса на сторожей; цена телефонного

оборудования уменьшается, сильно сокращая затраты на теле-

фонные услуги, что в свою очередь увеличивает спрос на спе-

циалистов по маркетингу на телевидении.

ЭЛАСТИЧНОСТЬ

СПРОСА НА РЕСУРС

Высказанные выше соображения имеют непосред-

ственное отношение к смещению кривых спроса на

ресурс. Такие изменения спроса следует четко от-

личать от изменения количества требуемого ресур-

са. Последнее, напомним, не вызывает смещения

кривой спроса на ресурс, а приводит к перемеще-

нию из одной точки в другую на кривой устойчиво-

го спроса вследствие изменения цены на конкрет-

ный ресурс. Проиллюстрируем это утверждение: в

табл. 27-1 и на рис. 27-1 мы отмечали, что возрас-

тание ставки заработной платы с 5,95 до 7,95 дол.

приведет к снижению числа требуемых рабочих с

пяти до четырех человек.

Возникает вопрос: что определяет чувствитель-

ность производителей к изменениям цены ресурса?

Если использовать специальную терминологию —

что определяет эластичность спроса на ресурс, ины-

ми словами, чем определяется отношение измене-

ния объема спроса на ресурс к изменению его цены?

Некоторые устоявшиеся положения позволяют глуб-

же проникнуть в суть проблемы при ответе на дан-

ный вопрос.

Коэффициент снижения

МР.

Важен также такой

специфический показатель, как коэффициент

(темп) сокращения предельного продукта перемен-

ного ресурса. Если предельный продукт труда мед-

ленно сокращается по мере добавления труда к фик-

сированному объему капитала, то MRP, или кривая

спроса на труд, будет снижаться медленно и иметь

тенденцию поддерживать высокую эластичность.

Незначительное снижение цены на такой ресурс

приводит к относительно большому возрастанию

спроса на этот ресурс. И наоборот, если предельная

производительность труда резко падает, то MRP, или

кривая спроса на труд, быстро снижается. Это оз-

начает, что относительно значительное снижение

ставки заработной платы сопровождается весьма

небольшим повышением числа нанимаемых работ-

ников, то есть спрос на этот вид ресурса будет не-

эластичным.

Легкоеib

замещения

ресурса. Степень, с которой

ресурсы могут взаимно замещаться, является важ-

ным показателем эластичности. Чем больше имеет-

ся подходящих заменителей конкретного ресурса, тем

выше эластичность спроса на этот ресурс. Если про-

изводитель мебели считает, что пять или шесть раз-

личных пород дерева в равной степени подходят для

изготовления кофейных столиков, то повышение

цены на одну из них может вызвать резкое падение

спроса на нее, так как производитель может легко

заменить эту породу дерева. В другом крайнем слу-

чае замещение может оказаться невозможным: без

бокситов абсолютно невозможно производить алю-

миний. Это значит, что спрос на бокситы со сторо-

ны производителей алюминия имеет тенденцию

быть очень неэластичным.

Важно заметить, что особую роль в процессе

замещения ресурсов играет время. Например, води-

тели грузовиков какой-нибудь фирмы могут добить-

ся существенного повышения заработной платы при

незначительном или наступающем не сразу сниже-

нии занятости. Через некоторое время по мере из-

нашивания грузовики заменяют новыми, фирма

закупает машины большей грузоподъемности и тем

самым обеспечивает доставку того же количества

продукции с меньшим числом водителей. Кроме

того, фирма может применять иные средства транс-

порта. Другой пример: кабина нового пассажирского

реактивного самолета сконструирована для двух пи-

лотов, а не для трех, как это было ранее.

)

>.i

'„чши;

-ириса

на

яролукт.

Эластичность

спроса на какой-либо ресурс зависит от эластично-

сти спроса на производимый с его помощью про-

дукт. Чем выше эластичность спроса на продукт, тем

выше эластичность спроса на ресурс. Производный

характер спроса на ресурс должен был подвести нас

к ожиданию подобной же взаимозависимости. Не-

большое повышение цены продукта с высокой эла-

стичностью спроса вызывает резкое снижение объ-

ема продукции и соответственно достаточно боль-

шое сокращение объемов различных ресурсов, на

которые предъявляется спрос. Это обстоятельство

со всей очевидностью наводит на мысль, что спрос

на данный ресурс является эластичным.

Вспомним, что кривая спроса на ресурсы на

рис. 27-1 более эластична, чем кривая спроса на ре-

сурсы, показанная на рис. 27-2. Различие возника-

ет из-за того, что на рис. 27-1 мы предполагаем на-

личие абсолютно эластичной кривой спроса на про-

ГЛАВА 27

дукцию,

в то время как рис. 27-2 основан на нисхо-

дящей, или не вполне эластичной, кривой спроса

на продукцию.

4. Соотношение издержек на труд и совокупных из-

держек. Наконец, чем больше совокупных издержек

производства приходится на какой-то ресурс, тем

выше эластичность спроса на данный ресурс. Логиче-

ское обоснование этого утверждения вполне оче-

видно. В предельном случае, если затраты на труд

были бы единственным видом производственных

издержек, то 20%-ное повышение ставки заработ-

ной платы вызвало бы сдвиг вверх кривой издержек

фирмы на 20%. При заданной эластичности спроса

на продукт такой существенный рост издержек при-

вел бы к достаточно ощутимому снижению продаж

и резкому сокращению количества требуемого тру-

да. Спрос на труд был бы тогда эластичным. Но если

бы затраты на труд составили 50% издержек произ-

водства, то 20%-ный рост ставки заработной платы

вызвал бы повышение совокупных издержек толь-

ко на 10%. При той же самой эластичности спроса

на продукт последовало бы относительно неболь-

шое сокращение продаж и соответственно умень-

шение количества труда. Спрос на труд был бы в

таком случае неэластичным. {Ключевой вопрос 4.)

повторение

Ж?Щ.

• Кривая спроса на ресурс будет сдвигаться из-

за изменений спроса на продукцию, изменений про-

изводительности ресурса и изменений цен других

ресурсов.

"•"

Если ресурсы А

заменяют друг друга, то

снижение цены ресурса А уменьшит спрос на ре-

сурс В, когда эффект замещения превышает эффект

производства. Но если эффект объема производства

превышает эффект замещения, то спрос на ресурс В

увеличится.

• Если ресурсы С

D являются дополняющими,

то снижение цены ресурса С вызовет увеличение спро-

са на ресурс D.

Эластичность спроса на ресурс будет тем мень-

ше, чем быстрее происходит уменьшение предельно-

го продукта, чем меньше число заменителей, чем

ниже эластичность спроса на продукцию и чем мень-

ше доля издержек на ресурсы в валовых производст-

венных издержках.

ОПТИМАЛЬНОЕ СООТНОШЕНИЕ

РЕСУРСОВ

До сих пор наши рассуждения относились только к

одному переменному фактору производства, а имен-

но к труду. Но известно, что в долгосрочном плане

605

Производство и спрос на ресурсы

фирмы могут изменять количество всех применяе-

мых ресурсов. Поэтому важно научиться понимать,

какое сочетание ресурсов выберет фирма, если все

ресурсы будут переменными. Хотя в анализе мы

продолжаем рассматривать случай только с двумя

видами ресурсов, его выводы можно отнести к лю-

бому числу видов ресурсов.

Рассмотрим далее два взаимосвязанных вопроса.

1. Каким должно быть сочетание ресурсов

дчя

производства любого данного объема продукции с

наименьшими издержками?

2. Какое сочетание ресурсов будет максимизи-

ровать прибыль фирмы?

Правило наименьших издержек

Фирма производит любой заданный объем продук-

ции при комбинации ресурсов, обеспечивающей на-

именьшие издержки, когда последний доллар, за-

траченный на каждый ресурс, создает одинаковый

предельный

хпродукт.

Другими словами, издержки

на

производство

любого объема продукции миними-

зируются, если предельный продукт на доллар стои-

мости каждого применяемого ресурса будет одина-

ковым. В случае использования только двух ресур-

сов — труда и капитала — минимизация издержек

наступает тогда, когда:

МР труда МР капитала

Цена труда Цена капитала

Нетрудно увидеть, почему выполнение этого ус-

ловия означает производство с наименьшими затра-

тами. Предположим, например, что цена капитала

и труда составляет по доллару на единицу продук-

ции, но капитал и труд применяются в таких коли-

чествах, что предельный продукт капитала состав-

ляет 5, а предельный продукт труда равен 10. Исходя

из уравнения (1) становится ясно, что данное сочета-

ние не обеспечивает производства продукции с наи-

меньшими издержками:

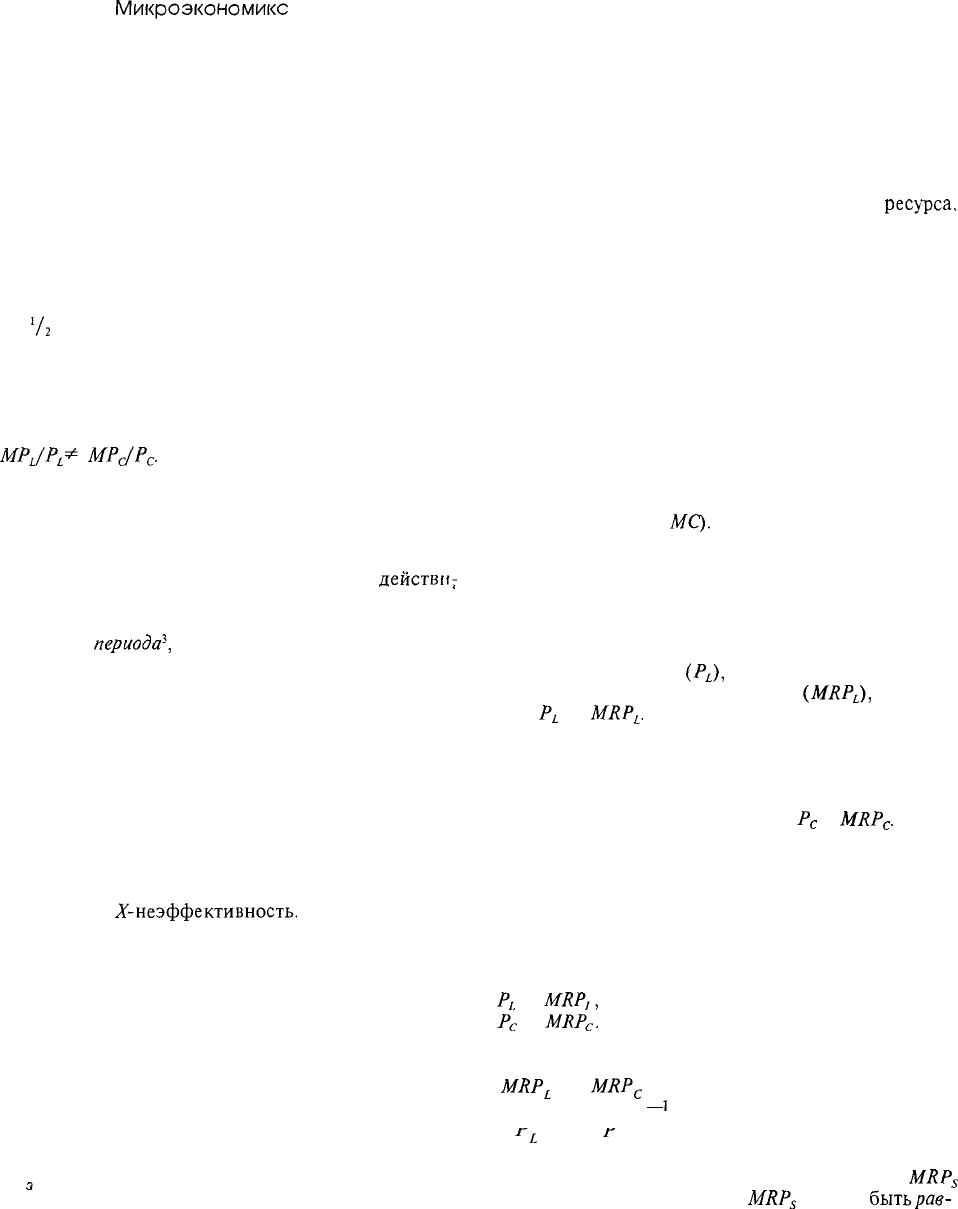
MPJP

составляет 10/1, а

МР

/Р

-5/1.

Если фирма затрачивает на капитал на доллар

меньше и расходует этот доллар на труд, то она те-

ряет пять единиц продукции, произведенных с по-

мощью капитала стоимостью в один предельный

доллар, а получает 10 единиц продукции от найма

труда на дополнительный доллар. Чистый объем

продукции увеличивается на 5 (10 — 5) единиц при

тех же общих затратах. Заметим, что перелив 1 дол

из затрат на капитал в затраты на труд приводит к

тому, что для данной фирмы кривая МР труда сме-

щается вниз, а кривая МР капитала — вверх, и фир-

ма продвигается к состоянию равновесия, где вы-

полняются условия уравнения (1). В этой точке МР

как труда, так и капитала может быть равно, напри-

мер, семи.

606

ЧАСТЬ ШЕСТАЯ

Микроэкономике

рынков ресурсов

Хотя при одинаковых совокупных затратах по-

лучается больше продукции, само собой разумеет-

ся, что затраты на единицу, а соответственно и со-

вокупные затраты на любой данный уровень объе-

ма производства сокращаются. Иначе говоря, про-

извести больший объем продукции при заданной ве-

личине совокупных издержек означает то же самое,

что производить заданный объем продукции при

меньшей величине совокупных издержек. Посмот-

рим на это с несколько иной позиции: если фирма

покупает на 1 дол. меньше капитала, ее производ-

ство сократится на пять единиц. Потратив допол-

нительно только 50 центов на труд, фирма увеличит

свое производство на недостающие пять единиц

'/,

от предельного продукта труда, стоящего

1 дол.). Таким образом, фирма может обеспечить

такой же суммарный объем продукции с издержка-

ми на 50 центов меньше.

И как мы видели, затраты на производство лю-

бого объема продукции можно сокращать, если

MPJP

НО когда перелив долларов меж-

ду капиталом и трудом достигает точки, в которой

удовлетворяются требования уравнения (1), то уже

не происходит никаких изменений в размерах при-

меняемого капитала и труда, которые вызывали бы

снижение издержек. Такому объему продукции со-

ответствует сочетание капитала и труда,

действи

тельно обеспечивающее наименьшие издержки.

При построении всех графиков издержек для дол-

госрочного

периода

описанных в главе 22 и использо-

ванных в последующих главах, посвященных пробле-

мам рынка продукта, предполагалось, что каждый по-

тенциально возможный уровень объема продукции до-

стигается при таком сочетании факторов производ-

ства, что издержки будут минимальными. Если бы

это было не так, то, по всей вероятности, существо-

вал бы более низкий предельный уровень графиков

издержек и соответственно был бы и другой (боль-

ший) объем продукции и более низкие цены в точ-

ке равновесия. С точки зрения положений главы 24

фирме, применявшей ресурсы в нарушение прави-

ла производства с наименьшими издержками, была

бы присуща

^-неэффективность.

Заметим, что правило производства с наимень-

шими издержками аналогично правилу максимиза-

ции полезности для потребителя, изложенному в

главе 21. Для достижения максимума полезности

при выборе товаров потребитель учитывает как свои

предпочтения, отраженные в данных об убывающей

предельной полезности, так и цены на различные

продукты. Производитель желает минимизировать

затраты аналогично тому, как потребитель стремит-

ся максимизировать полезность. Пытаясь найти

оптимальное соотношение ресурсов, производитель

должен учитывать как производительность ресур-

са — что находит отражение в данных об убываю-

щей предельной производительности, - так и цены

(издержки) на различные ресурсы. Фирма может

считать, что выгодно использовать очень неболь-

шой объем исключительно продуктивного ресурса,

даже если его цена будет достаточно высокой. И на-

оборот, фирма может разумно использовать боль-

шой объем относительно непродуктивного

ресурса,

если его цена окажется достаточно низкой.

Правило максимизации прибыли

Чтобы максимизировать прибыль, недостаточно

только минимизировать издержки. Существует мно-

го различных уровней производства, при которых

фирма может производить продукт с наименьшими

издержками. Но есть только один-единственный

уровень производства, при котором прибыль будет

действительно максимальной. Из предыдущего ана-

лиза рынков продуктов следует, что производство

продукции с максимальной прибылью достигается

тогда, когда предельный доход равен предельным

издержкам (MR =

МС).

Давайте теперь сформули-

руем правило достижения этого равенства с точки

зрения затрат ресурсов.

При составлении графика спроса на труд в на-

чале данной главы мы установили, что количество

труда, обеспечивающее максимальную прибыль,

должно быть таким, чтобы ставка заработной пла-

ты, или цена труда

была равна предельному

продукту труда в денежной форме

(MRP

или про-

ще:

MRP

Такое же логическое обоснование применимо к

любому другому ресурсу, например капиталу. Капи-

тал также будет использован в максимизирующем

прибыль объеме, когда его цена равна предельному

продукту в денежной форме, или

MRP

Таким

образом, в целом можно сказать, что при использо-

вании ресурсов на конкурентных рынках фирма ре-

ализует комбинацию ресурсов, обеспечивающую мак-

симальную прибыль, если каждый вводимый фактор

производства используется до точки, в которой его

цена равна издержкам на получение предельного

дохода:

Р,.

MRP,,

MRP

Иначе это правило можно записать так:

MRP

Р Р

]

(2)

Мы специально указываем долгосрочный период, так как, со-

гласно правилу наименьших издержек, количество труда и количе-

ство капитала являются переменными величинами.

В уравнении (2) обратите внимание на то, что

недостаточно установить пропорцию между

MRP

обоих ресурсов и ценами; их

MRP

должны

§ытърав-

ны ценам, тогда эти соотношения будут равны еди-

ГЛАВА 27

нице. Например, если

MRP

= 15 дол.,

= 5 дол.,

MRP

= 9 дол. и

= 3 дол., то фирма недоисполь-

зует как капитал, так и труд, хотя отношения MRP

к цене на ресурс одинаковы для обоих ресурсов. Это

означает, что фирма могла бы увеличивать прибыль

путем привлечения дополнительного количества

капитала и труда до тех пор, пока снижающиеся

кривые MRP капитала и труда не достигнут точки,

в которой

MRP

равно 5 дол., a

MRP

— 3 дол. Те-

перь эти соотношения приняли бы такой вид —

Уз,

что в каждом случае равно единице

Следует добавить небольшое, но важное замеча-

ние. Для простоты изложения мы разделили эти

задачи, но положение уравнения (2) о максимиза-

ции прибыли включает положение уравнения (1) о

производстве с наименьшими издержками. Обрати-

те внимание: если мы разделим числители MPR в

уравнении (2) на цену продукта, то получим урав-

нение (1). Иными словами, фирма, стремящаяся к

максимизации прибыли, должна производить про-

дукцию при таком соотношении затрат на ресурсы,

которое обеспечивало бы также наименьшие из-

держки. Если фирма не применяет обеспечивающе-

го наименьшие издержки соотношения труда и ка-

питала, то она, конечно, может получить тот же

объем производства с несколько меньшими сово-

Нетрудно показать, что уравнение (2) не противоречит [а на

самом деле эквивалентно) правилу Р = МС, применяемому при оп-

ределении объема производства продукции с максимальной при-

былью, с чем вы встречались в главе 23 Возьмем обратные вели-

чины уравнения (2)

р р

-LJ—=

MRP

Вспомним, что в условиях совершенной конкуренции на рынке

предельный доход в денежной форме,

MRP,

находят путем умноже-

ния величины предельного продукта

МР

на цену продукта

Поэто-

му можно записать такое уравнение

р р

-=1.

Умножив обе части равенства на цену продукта

получаем

Р, Р

МР

Эти два соотношения определяют предельные издержки Ины-

ми словами, если мы разделим величину затрат

(цену)

на дополни-

тельную единицу труда или капитала на соответствующий предель-

ный продукт, то получим значение приращения совокупных издер-

жек, то есть предельные издержки каждой дополнительной единицы

продукции Например, если цена труда дополнительного рабочего

(PJ

составляет

дол,

а предельный продукт

(MPJ

этого рабочего

равен, скажем, пяти единицам, то предельные издержки каждой из

этих пяти единиц будут составлять 2 дол Аналогичное обоснование

применимо и к капиталу Таким образом, получаем

МС

Наш вывод заключается в том, что уравнение (2), использован-

ное в анализе комбинации вводимых факторов производства, обес-

печивающей максимальную прибыль, эквивалентно ранее сформу-

лированному правилу Р = МС, характеризующему производство про-

дукции с максимальной прибылью

607

Производство и спрос на ресурсы

купными издержками и чуть большую прибыль. Та-

ким образом, необходимым условием максимизации

прибыли является соблюдение уравнения (1). Од-

нако уравнение (1) не является достаточным усло-

вием максимизации прибыли. Фирма вполне может

получать «неправильный» объем продукции, то есть

такой, который не приносит максимальной прибы-

ли, но обеспечивает соотношение ресурсов, обес-

печивающих наименьшие издержки.

Числовой пример

Возможно, полезным для понимания правил наи-

меньших затрат и максимизации прибыли окажет-

ся числовой пример. В столбцах (2), (3), (2'), (3')

табл. 27-4 даны значения совокупного и предельно-

го продукта для различных количеств труда и капи-

тала, которые, как предполагается, являются един-

ственными вводимыми факторами производства,

требующимися для изготовления продукта X. Оба

фактора производства подвержены действию зако-

на убывающей доходности.

Предполагается также, что труд и капитал про-

даются на конкурентных рынках ресурсов по 8 и

12 дол. соответственно, а продукт

продается в ус-

ловиях конкуренции по 2 дол. Что касается труда и

капитала, то мы можем определить совокупный

доход, получаемый за счет каждого фактора произ-

водства, путем умножения совокупного продукта на

цену продукта — 2 дол. (см. столбцы 4 и 4'). Это

позволяет вычислить издержки на продукт, прино-

сящий предельный доход, для каждой последующей

вводимой единицы труда и капитала, как показано

в столбцах (5) и (5').

Производство при наименьших затратах. Рассмотрим

следующий вопрос: какое соотношение затрат тру-

да и капитала обеспечивает наименьшие издержки

при производстве, скажем, 50 единиц продукции?

Ответ: три единицы труда и две единицы капитала.

Из столбцов (3) и

(З

)

видно, что при найме трех

единиц труда

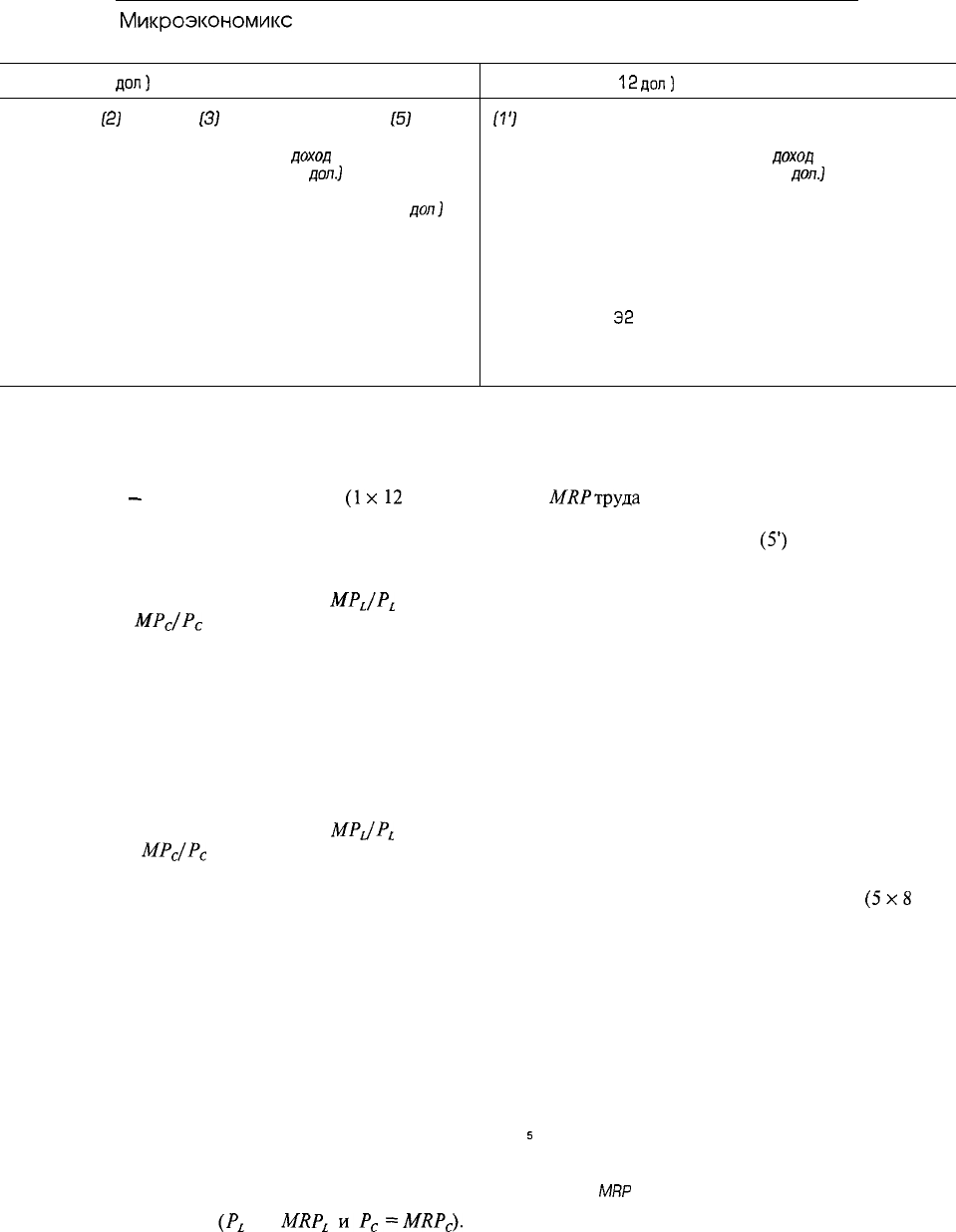
MPJP

= 6/8 = 3/4, а при использо-

вании двух единиц капитала

MPJP

= 9/12 = 3/4,

что отвечает условию уравнения (1). Столбцы (2) и

(2') показывают, что в результате такого соотноше-

ния труда и капитала мы получим указанные 50

(28 + 22) единиц продукции. Как можно проверить,

что издержки действительно являются минимальны-

ми? Сначала отметим, что совокупные издержки

использования трех единиц труда и двух единиц ка-

питала составляют 48 дол. ((3 х 8 дол.) + (2 х 12 дол.)),

таким образом, издержки на единицу продукции

равны 0,96 дол. (48 дол./50 дол.).

Заметьте, что существуют и другие соотношения

труда и капитала, которые также дают 50 единиц

продукции. Например, пять единиц труда и одна

единица капитала позволят произвести 50 единиц

21-

608 ЧАСТЬ ШЕСТАЯ

Микроэкономике

рынков ресурсов

Таблица 27-4. Соотношение труда и капитала, обеспечивающее наименьшие издержки и максимальную прибыль*

Труд (цена

(1)

Единицы

ресурса

= 8

дол)

IS)

Совокупный

продукт

13)

Предельный

продукт

(4)

Совокупный

доход

[в

доп.)

15)

Предельный

продукт

в денежной

форме

(в

дол)

6 .

Капитал

IV)

Единицы

ресурса

(цена =

дол)

(21

Совокупный

продукт

(31

Предельный

продукт

(41

Совокупный

доход

(в

дол.)

(51

Предельный

продукт

в денежной

форме

(в дол.)

* В целях упрощения в данной таблице предполагается, что производительность каждого ресурса не зависит от количества другого ресурса Например,

предполагается, что совокупный предельный продукт труда не изменяется с изменением обьема используемого капитала

(37 + 13), но мы видим, что теперь совокупные из-

держки выше

52 дол. ((5 х 8 дол.) +

(1x12

дол.)),

что означает возрастание средних издержек на еди-

ницу продукции до 1,04 дол. (52 дол./50). Обрати-

те внимание, что применение пяти единиц труда

и единицы капитала нарушает правило наимень-

ших издержек в том смысле, что

— 4/8,

меньше, чем

МР

/Р

= 13/12. Это означает, что

для производства указанного объема продукции

необходимо применять больше капитала и мень-

ше труда.

Аналогичным образом 50 единиц продукции точ-

но так же можно было бы произвести с помощью

двух единиц труда и трех единиц капитала: совокуп-

ные издержки на 50 единиц продукции также со-

ставили бы 52 дол. ((2 х 8 дол.) + (3 х 12 дол.)), или

1,04 дол. на единицу. Здесь условия уравнения (1)

не соблюдаются в том смысле, что

MPJP

= 10/8,

что превышает

МР

/Р

= 6/12. Данное неравенство

показывает, что фирме следует применять больше

труда и меньше капитала.

Суммируем наши выводы: хотя соотношения

труда и капитала для производства любого данного

объема продукции могут быть различные — в на-

шем случае 50 единиц, — но только одно соотноше-

ние, отвечающее условиям уравнения (1), будет дей-

ствительно минимизировать издержки.

Максимизация прибыли. Второй вопрос: принесут ли

50 единиц максимальную прибыль? Ответ: нет, ибо в

уравнении (2) не выполнено правило максимизации

прибыли при найме трех единиц труда и примене-

нии двух единиц капитала. Известно, что для макси-

мизации прибыли необходимо использовать любой

вводимый фактор производства до тех пор, пока его

цена не будет равна издержкам на продукт, принося-

щий предельный доход

—

MRP

и?

MRP

Но из столбца (5) видно, что при найме трех единиц

труда

MRPтруда

равен 12 дол., а его цена равна толь-

ко 8 дол. Это значит, что выгодно нанимать больше

труда. Аналогично из столбца

)

видно, что при ис-

пользовании двух единиц капитала MRP составляет

18 дол., а цена капитала - лишь 12 дол., что свиде-

тельствует о необходимости использовать больше

капитала. Иначе говоря, применяя три единицы тру-

да и две единицы капитала для производства 50 еди-

ниц, фирма недоиспользует оба фактора производ-

ства. Как труд, так и капитал потребляются в мень-

ших объемах, чем это необходимо для получения

максимальной прибыли.

Видно, что предельные продукты труда и капи-

тала в денежной форме равны их ценам; поэтому

условия уравнения (2) выполняются, если фирма по-

требляет пять единиц труда и три единицы капита-

ла. Следовательно, это и есть то соотношение ре-

сурсов, которое обеспечивает выпуск продукции с

максимальной прибылью

. Совокупные затраты

фирмы составят 76 дол., включая 40 дол.

(5x8

дол.)

стоимости труда и 36 дол. (3 х 12 дол.) стоимости

капитала. Совокупный доход в 130 дол. определяет-

ся путем умножения общего объема продукции,

65 единиц (37 + 28), на цену продукта - 2 дол., или,

что то же самое, просто суммируя совокупный до-

ход от труда (74 дол.) и капитала (56 дол.). Разность

между совокупным доходом и совокупными издерж-

ками, разумеется, и есть экономическая прибыль

фирмы, которая в данном примере равна 54 дол.

Если же мы имеем дело с дискретным (прерывистым) приро-

стом объемов продукции, то следует учесть, что применение четы-

рех единиц труда и двух единиц капитала тоже будет прибыльным

Говоря иначе,

MRP

пятой единицы труда и ее цена равны (8 дол ],

так что пятая единица не увеличивает и не уменьшает прибыль фир-

мы То же самое относится и к третьей единице капитала.

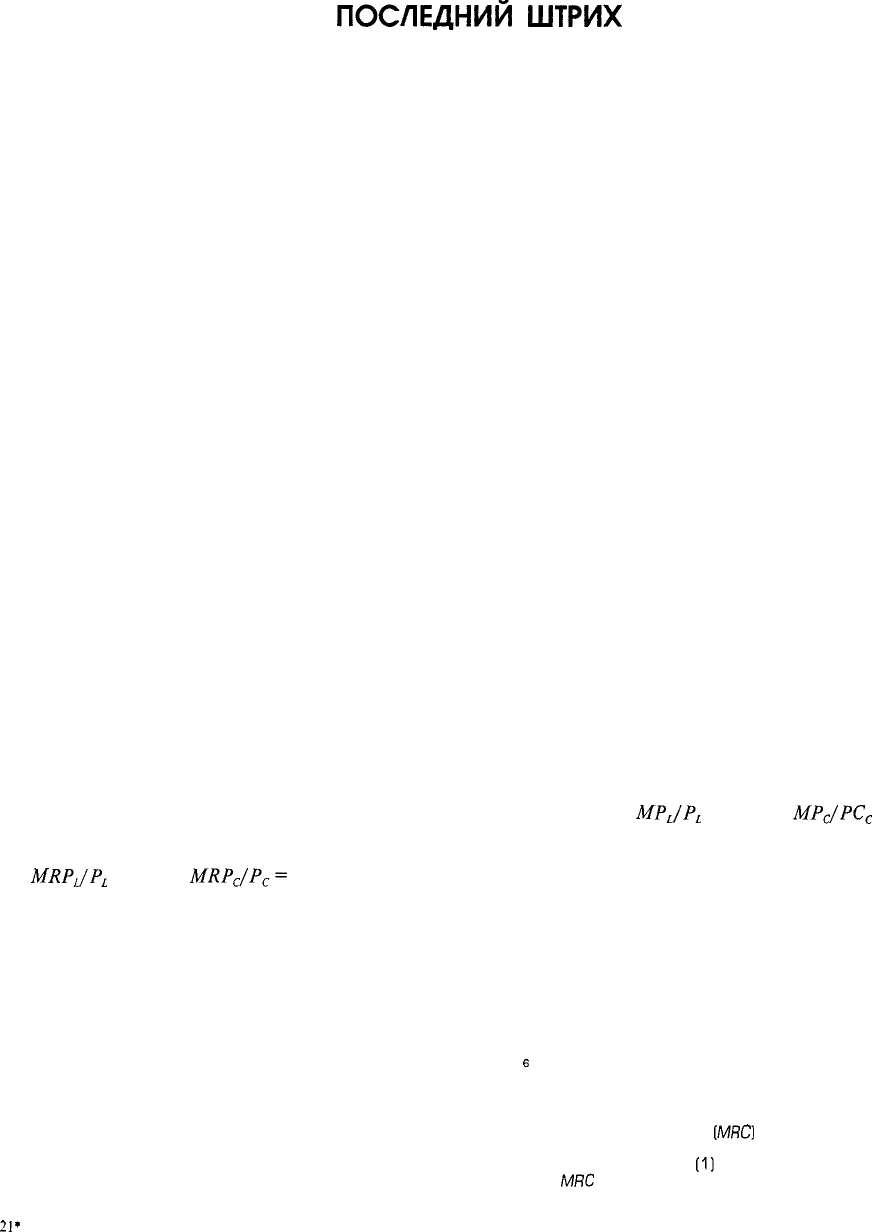
ГЛАВА 27

609

Производство и спрос на ресурсы

ПОСЛЕДНИЙ

ШТРИХ

ЗАМЕЩЕНИЕ ВВОДИМЫХ ФАКТОРОВ

ПРОИЗВОДСТВА: ПРИМЕР СЛУЖЕБНЫХ

ВАГОНОВ В ТОВАРНЫХ ПОЕЗДАХ

Вопрос о замещении вводимых факторов производст-

ва - особенно когда рабочие места находятся под угрозой

ликвидации - может быть довольно спорным.

Мы уже видели, что фирма достигнет оптимального со-

отношения вводимых факторов производства с наименьши-

ми издержками в том случае, если последний доллар, ис-

пользованный на каждый из этих факторов, обеспечит оди-

наковый вклад в общий объем продукции. Это правило, од-

нако, не служит препятствием тому, чтобы фирма могла из-

менять структуру вводимых факторов производства в связи

с технологическими нововведениями или изменениями в

ценах на вводимые факторы производства. К сожалению, в

действительности замещение старого капитала новым и

замена капитала трудом могут оказаться проблемными и

труднодостижимыми.

Рассмотрим случай с железнодорожными служебными

вагонами в товарных составах. Администрация железных

дорог заявляет, что с учетом технического прогресса нет

необходимости устраивать в товарных поездах служебные

вагоны. В частности, их следует заменить «релейной сис-

темой», которую можно установить на соединительном ус-

тройстве последнего вагона поезда. Этот небольшой «чер-

ный ящик» содержит вращающийся стробоскоп и приборы,

которые контролируют скорость поезда, давление в тормо-

зах, а также другие необходимые данные и передают их ма-

шинисту локомотива. Релейная система стоит всего

400 дол., а новый служебный вагон - 80 тыс. дол. И есте-

ственно, релейная система заменяет одного члена поезд-

ной бригады.

Железные дороги получили бы существенную экономию

на издержках - вероятно, 400 млн дол. в год - в результате

подобных изменений в соотношении факторов производства,

капитала и труда. Но Объединенный профсоюз работников

транспорта, представляющий интересы железнодорожных

проводников и кондукторов служебных вагонов, опасается, что

подобная тенденция повлечет за собой сокращение спроса

на членов его организации. Поэтому профсоюз сделал твер-

дую, но практически безуспешную попытку приостановить

ликвидацию служебных вагонов. Профсоюз утверждает, что

прекращение использования служебных вагонов приведет к

снижению безопасности на железных дорогах. Профсоюз

заявляет, что релейная система в отличие от людей не может

обнаруживать поломки в колесах, осях и перегрев подшип-

ников. С точки зрения администрации, такой подход выглядит

как попытка сохранить численность рабочей силы, независи-

мо от потребности в ней, то есть защитить рабочие места,

которые не являются более необходимыми. Администрация

утверждает, что, по имеющимся данным, безопасность обес-

печивается как при использовании служебных вагонов,

так и без них; фактически безопасность можно повысить и

без служебных вагонов, так как многие несчастные случаи

происходят и тогда, когда члены поездных бригад обслужи-

вают служебные вагоны.

Служебные вагоны практически не используются в Ев-

ропе, пока еще они используются в Канаде. В Соединенных

Штатах профсоюзы железнодорожников с помощью лобби-

стов протолкнули в четырех штатах закон, в соответствии с

которым служебные вагоны являются обязательными. Во

всех других штатах использование служебных вагонов в

товарных составах остается предметом переговоров при

заключении коллективных соглашений. В любом случае при-

мер со служебными вагонами показывает, что замещение

вводимых факторов производства является не таким про-

стым делом, как это следует из экономического анализа.

(130 дол. — 76 дол.). Обратите внимание, что усло-

вия уравнения (2) выполняются, если фирма при-

меняет пять единиц труда и три единицы капита-

ла:

MRPJP

= 8/8 =

MRPJP

12/12 = 1. Читате-

лю необходимо поэкспериментировать с другими

соотношениями труда и капитала, чтобы самосто-

ятельно убедиться в том, что при ином сочетании

ресурсов экономическая прибыль будет меньше

54 дол.

Наш пример подтверждает вышеприведенное

утверждение о том, что фирма, которая использует

факторы производства в таком соотношении, ко-

торое обеспечивает максимальную прибыль, непре-

менно производит продукцию также и с наимень-

шими издержками. Таким образом, удовлетворяя

условиям уравнения (2), фирма автоматически

удовлетворяет условиям уравнения (1). В данном

случае видно, что для пяти единиц труда и трех еди-

ниц капитала

MPJP

= 4/8 =

МР

/РС

= 6/12

(Ключевые вопросы 5 и 7.)

РАСПРЕДЕЛЕНИЕ ДОХОДОВ

В СООТВЕТСТВИИ С ТЕОРИЕЙ

ПРЕДЕЛЬНОЙ ПРОИЗВОДИТЕЛЬНОСТИ

В анализе формирования цен на ресурсы раскрыва-

ется обоснование положения о том, что экономиче-

ская справедливость является одним из признаков

Примечание 1 в главе 28 модифицирует наши правила о на-

именьших издержках и максимальной прибыли в случае, когда фир-

ма использует ресурсы в условиях несовершенной конкуренции. Там,

где на рынке ресурсов существует несовершенная конкуренция,

предельные издержки на ресурс

[MRC]

- издержки на дополнитель-

ный вводимый фактор производства - превышают цену ресурса [Р].

Следовательно, в уравнениях

(1)

и (2) мы должны заменить в зна-

менателе

MRC

на Р.

21*

ЧАСТЬ ШЕСТАЯ

610

Микроэкономике

рынков ресурсов

конкурентной капиталистической экономики. Из

табл. 27-1 следует, что работник, в сущности, полу-

чает заработную плату, равную его предельному вкла-

ду в доход фирмы. Проще говоря, работнику выпла-

чивают столько, сколько стоит его труд. Соответст-

венно если кто-то разделяет этический принцип

«каждому — в соответствии с тем, что он создает», то

теория предельной производительности, по всей ви-

димости, и дает честное и справедливое обоснова-

ние распределения дохода. Поскольку теория пре-

дельной производительности в равной степени при-

менима к капиталу и земле, то распределение всех

доходов можно считать справедливым.

На первый взгляд распределение, при котором

работники и владельцы материальных ресурсов по-

лучают вознаграждение в соответствии с их вкла-

дом в производство продукции, звучит справедли-

во. Но распределение доходов в соответствии с тео-

рией предельной производительности подвергается

серьезной критике.

1. Неравенство. Критики утверждают, что распреде-

ление доходов согласно теории предельной произ-

водительности характеризуется значительным нера-

венством, в первую очередь из-за неравенства в рас-

пределении производственных ресурсов. Помимо

того что все индивиды имеют различные унаследо-

ванные способности, они сталкиваются с разными

возможностями повышения производительности че-

рез систему образования и переподготовки. Некото-

рые члены общества могут вообще оказаться неспо-

собными участвовать в производстве из-за умствен-

ной и физической недееспособности и не получать

никакого дохода в системе распределения, основан-

ной исключительно на теории предельной произво-

дительности. Собственность на ресурсы характери-

зуется также большим неравенством. Многие земле-

владельцы и капиталисты владеют собственностью

по наследству, а не в результате своих производст-

венных усилий. Значит, доход от унаследованной соб-

ственности на ресурсы противоречит принципу «каж-

дому - в соответствии с тем, что он

создает».

Подоб-

ная аргументация может подвести к утверждению,

что необходимо изменить государственную полити-

ку распределения доходов, исходя из одной только

теории предельной производительности.

2. Монопсония и монополия. Теория предельной

производительности основывается на предположе-

нии о конкурентных рынках. В главе 28 мы увидим,

что рынки труда, например, очищаются от «несо-

вершенств». Некоторые наниматели проявляют

власть типа монопсонии при найме работников.

А при продаже своих услуг некоторые работники че-

рез профсоюзы и профессиональные ассоциации

противостоят монопольной силе. Фактически про-

цесс заключения коллективных договоров о зара-

ботной плате представляет собой борьбу за контроль

над распределением дохода. В этой борьбе рыноч-

ные силы — и доля дохода от предельной произво-

дительности — отходят на задний план. В действи-

тельности, в силу несовершенной конкуренции на

рынке ставки заработной платы и цены на другие

ресурсы зачастую не отражают реального вклада

факторов производства в производство всей продук-

ции страны.

РЕЗЮМЕ

1. Цены на ресурсы являются основным факто-

ром, определяющим денежные доходы, и одновре-

менно они выполняют функцию распределения ре-

сурсов по различным отраслям и фирмам.

2. Тот факт, что спрос на любой ресурс является

производным от спроса на выпускаемый с его по-

мощью продукт, наводит на мысль, что спрос на ре-

сурс будет зависеть от производительности и ры-

ночной стоимости (цены) товара, который произ-

водится с помощью этого ресурса.

3. График предельного продукта любого ресурса

в денежной форме представляет собой график спро-

са на данный ресурс. Это вытекает из правила, со-

гласно которому фирме в условиях конкуренции на-

иболее выгодно применять ресурс до такой точки, в

которой цена на ресурс равна предельному продукту

в денежной форме.

4. Кривая спроса на ресурс отлого понижается,

поскольку предельный продукт дополнительно вво-

димых единиц любого ресурса понижается в соответ-

ствии с законом убывающей доходности. Если фирма

продает продукцию на рынке в условиях несовершен-

ной конкуренции, то кривая спроса на ресурс падает

еще и по другой причине: цена на продукт должна

снижаться, чтобы фирма могла продать больше про-

дукции. Рыночный спрос на ресурс можно опреде-

лить путем суммирования по горизонтали кривых

спроса всех фирм, потребляющих указанный ресурс.

5. Спрос на ресурс будет изменяться, то есть

кривая спроса на ресурс будет перемещаться, в ре-

зультате: а) изменения спроса, а соответственно, и

цены на продукт, который производится с помо-

щью данного ресурса; б) изменений производитель-

ности ресурса либо в связи с ростом количества и

повышения качества других ресурсов, в сочетании

с которыми используется данный ресурс, либо в

связи с повышением качества самого указанного

ресурса; в) изменений цен других ресурсов.