Lyons W.C. (ed.). Standard handbook of petroleum and natural gas engineering.2001- Volume 1
Подождите немного. Документ загружается.


Geometry
5
L
=
q/l80*nr
Some of the properties of arcs are defined by the following theorems:
1.
In congruent circles,
if
two chords are congruent,
so
are the corresponding
minor arcs.
2.
Tangent-Secant Theorem-If given an angle with its vertex on a circle, formed
by a secant ray and a tangent ray, then the measure of the angle is half
the measure of the intercepted arc.
3.
Two-Tangent Power Theorem-The two tangent segments to a circle from an
exterior point are congruent and determine congruent angles with the
segment from the exterior point to the center of the circle.
4.
Two-Secant Power Theorem-If given a circle
C
and an exterior point
Q,
let
L,
be a secant line through
Q,
intersecting
C
at points
R
and
S,
and let
L,
be another secant line through Q, intersecting
C
at U and T, then
QR
QS
=
QU QT
5.
Tangent-Secant Power Theorem-If given a tangent segment QT to a circle
and a secant line through
Q,
intersecting the circle at
R
and
S,
then
QR
QS
=
QT2
-
-
6.
Two-Chord Power Theorem-If
RS
and TU are chords of the same circle,
intersecting at
Q,
then
QR
QS
=
QU QT
Concurrency
Two or more lines are concurrent if there is a single point which lies on all
of them. The three altitudes of a triangle (if taken as lines, not segments) are
always concurrent, and their point of concurrency is called the orthocenter. The
angle bisectors of a triangle are concurrent at a point equidistant from their
sides, and the medians are concurrent two thirds of the way along each median
from the vertex to the opposite side. The point of concurrency of the medians
is the centroid.
Similarity
Two figures with straight sides are similar
if
corresponding angles are con-
gruent and the lengths of corresponding sides are in the same ratio.
A
line
parallel to one side of a triangle divides the other two sides in proportion,
producing a second triangle similar to the original one.
Prisms and Pyramids
A
prism is
a
three dimensional figure whose bases are any congruent and
parallel polygons and whose sides are parallelograms.
A
pyramid is a solid with
one base consisting of any polygon and with triangular sides meeting at a point
in a plane parallel to the base.
Prisms and pyramids are described by their bases: a triangular prism has a
triangular base, a parallelpiped is a prism whose base is a parallelogram and a

6
Mathematics
rectangular parallelpiped
is a right rectangular prism. A cube is a rectangular
parallelpiped all of whose edges are congruent. A
triangular pyramid
has a
triangular base, etc. A
circular cylinder
is a prism whose base is a circle and a
circular cone
is a pyramid whose base is a circle.
Coordinate Systems
Each point on a plane may be defined by a pair
of
numbers. The coordinate
system
is
represented by a line
X
in the plane (the
x-axis)
and by a line
Y
(the
y-axis)
perpendicular to line
X
in the plane, constructed
so
that their intersection,
the
origin,
is denoted by zero. Any point P on the plane can now be described
by its two coordinates which form an ordered pair,
so
that P(x,,y,) is a point
whose location corresponds to the real numbers x and
y
on the x-axis and
the y-axis.
If the coordinate system is extended into space, a third axis, the z-axis,
perpendicular to the plane of the xI and
y,
axes, is needed to represent the
third dimension coordinate defining a point P(x,,y,,z,). The z-axis intersects the
x and
y
axes at their origin, zero. More than three dimensions are frequently
dealt with mathematically, but are difficult
to
visualize.
The
slope
m of a line segment in a plane with end points P,(x,,y,) and P,(x,,y,)
is determined by the ratio of the change in the vertical
(y)
coordinates to the
change in the horizontal (x) coordinates or
m
=
(Y'
-
YI)/(X2
-
XI)
except that a vertical line segment (the change in x coordinates equal to zero)
has no slope, i.e., m is undefined. A horizontal segment has a slope
of
zero.
Two
lines with the same slope are parallel and two lines whose slopes are
negative reciprocals are perpendicular to each other.
Since the distance between two points P,(x,,y,) and P,(x,,y,) is the hypotenuse
of a right triangle, the length of the line segment PIP, is equal to
Graphs
A
graph
is a figure, i.e., a set of points, lying in a coordinate system and a
graph of a condition (such as
x
=
y
+
2)
is the set of all points that satisfy the
condition. The graph of the
slope-intercept equation,
y
=
mx
+
b,
is the line which
passes through the point (O,b), where b is the y-intercept (x
=
0)
and m is the
slope. The graph of the equation
(x
-
a)'
+
(y
-
b)'
=
r2
is a circle with center (a,b) and radius r.
Vectors
A
vector
is described
on
a coordinate plane by a
directed segment
from its initial
point to its terminal point. The directed segment represents the fact that every
vector determines not only a magnitude, but also a direction. A vector
v
is not
Geometry
7
changed when moved around the plane, if its magnitude and angular orientation
with respect to the x-axis is kept constant. The initial point of v may therefore
be placed at the origin
of
the coordinate system and?’may be denoted by
d=
<
a,b
>
where a is the x-component and b is the y-component of the terminal point.
The magnitude may then be determined by the Pythagorean theorem
For every pair of vectors (xI,yI) and (x2,y2), the
vector
sum
is given by (x,
+
xp,
y1
+
y2).
The
scalar product
of a vector P
=
(x,y) and a real number (a
scalar)
r
is rP
=
(rx,ry). Also see the discussion of polar coordinates in the section
“Trigonometry” and Chapter
2,
“Basic Mechanics.”
Lengths and Areas
of
Plane Figures
[l]
(For definitions of trigonometric functions, see “Trigonometry.”)
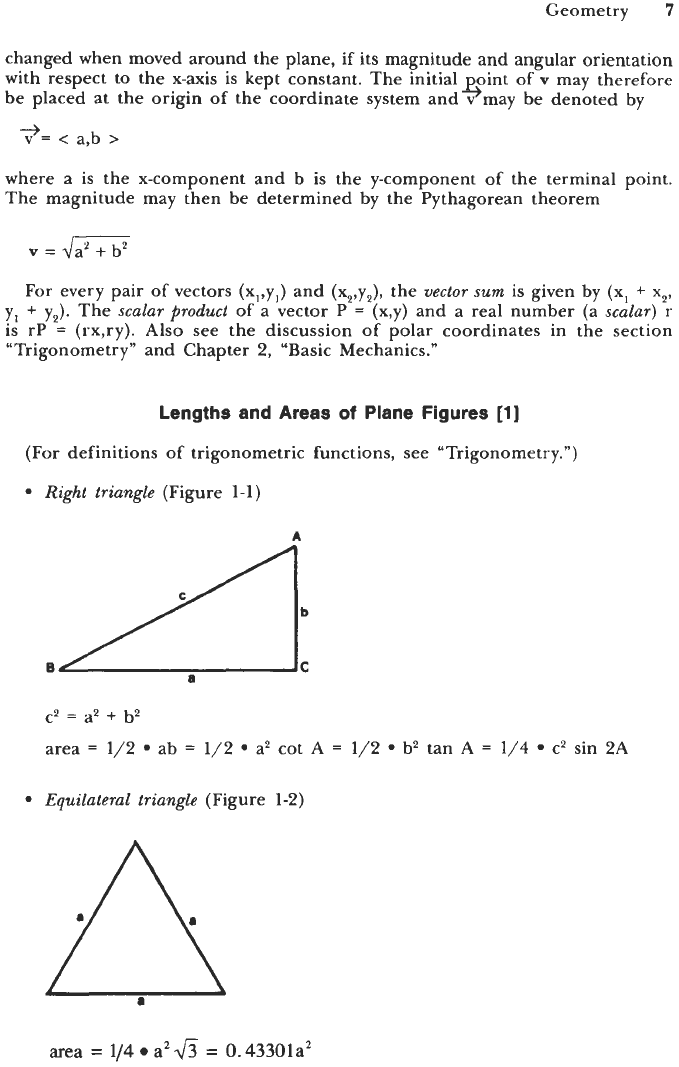
Right triangle
(Figure
1-1)
A
c2
=
a2
+
b2
area
=
1/2
ab
=
1/2
a2 cot
A
=
1/2
b2 tan A
=
1/4
c2 sin
2A
Equilateral triangle
(Figure
1-2)
area
=
114 a2
&
=
0.
43301a2

8
Mathematics
Any triangle
(Figure 1-3.)
A
area
=
1/2
base altitude
=
1/2
ah
=
1/2
ab sin
C
=
-
+
1/2
{(XIY2
-
$yI)
+
(XZYS
-
X.SY2)
+
(XSYI
-
XIY,))
where
(x,,yl),
(xz,yz),
(x,,y,)
are coordinates
of
vertices.
Rectangle
(Figure
1-4)
area
=
ab
=
1/2
D2
sin
u
where
u
=
angle between diagonals
D,
D
Rhombus
(Figure
1-5)
Area
=
a'sin C
=
1/2
DID,
where
C
=
angle between two adjacent sides
D,,
D,
=
diagonals
Parallelogram
(Figure
1-6)
c
\
Geometry
9
area
=
bh
=
ab sin c
=
1/2
D,D,
sin
u
where
u
=
angle between diagonals
D,
and
D,
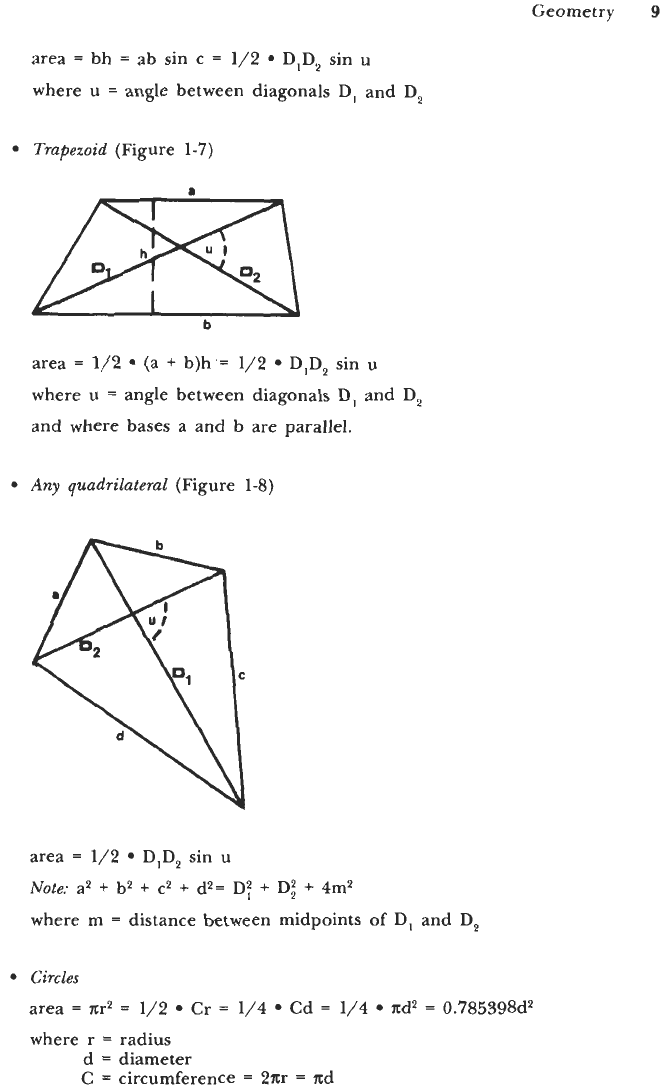
Trapezoid
(Figure 1-7)
area
=
1/2
(a
+
b)h'=
1/2
D,D,
sin
u
where
u
=
angle between diagonals
D,
and
D,
and where bases a and b are parallel.
Any
quadrilateral
(Figure 1-8)
area
=
1/2
D,D,
sin
u
Note:
a2
+
b2
+
c2
+
d*=
D2
+
D*
+
4m*
12
where
m
=
distance between midpoints of
D,
and
D,
Circles
area
=
nr2
=
1/2
Cr
=
1/4 Cd
=
1/4
nd2
=
0.785398d2
where r
=
radius
d
=
diameter
C
=
circumference
=
2nr
=
nd
10
Mathematics
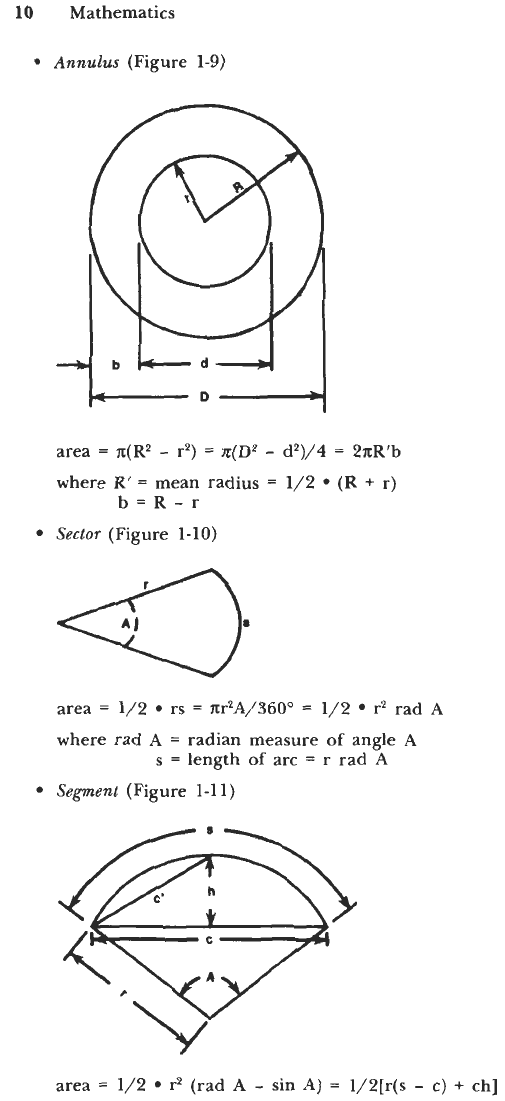
Annulus
(Figure
1-9)
area
=
n(R2
-
r2)
=
n(D2
-
d2)/4
=
2nR'b
where
R'
=
mean radius
=
1/2 (R
+
r)
b=R-r
Sector
(Figure
1-10)
area
=
1/2
0
rs
=
xr2A/36O0
=
1/2
r2
rad
A
where rad A
=
radian measure
of
angle
A
s
=
length
of
arc
=
r
rad A
Segment
(Figure
1-11)
area
=
1/2
r2
(rad A
-
sin A)
=
1/2[r(s
-
c)
+
ch]

Geometry
11
where rad
A
=
radian measure of angle
A
For small arcs,
s
=
1/3
(8~‘
-
C)
where c’
=
chord of half of the arc (Huygen’s approximation)
Note:
c
=
22/ho
c’
=
Jdh
or
d
=
d2/h
where d
=
diameter of circle
h
=
r[l
-
cos
(1/2
A)]
s
=
2r
rad
(1/2
A)
Ellipse
(Figure
1-12)
area of ellipse
=
nab
area of shaded segment
=
xy
+
ab sin-’ (x/a)
length
of
perimeter
of
ellipse
=
x(a
+
b)K,
where
K
=
(1
+
1/4
m2
+
1/64
m4
+
1/256
m6
+
. .
.)
m
=
(a
-
b)/(a
+
b)
For m
=
0.1
0.2 0.3 0.4 0.5
For m
=
0.6
0.7
0.8
0.9
1
.0
K
=
1.002
1.010 1.023
1.040 1.064
K
=
1.092 1.127
1.168 1.216
1.273
Hyperbola
(Figure
1-13)
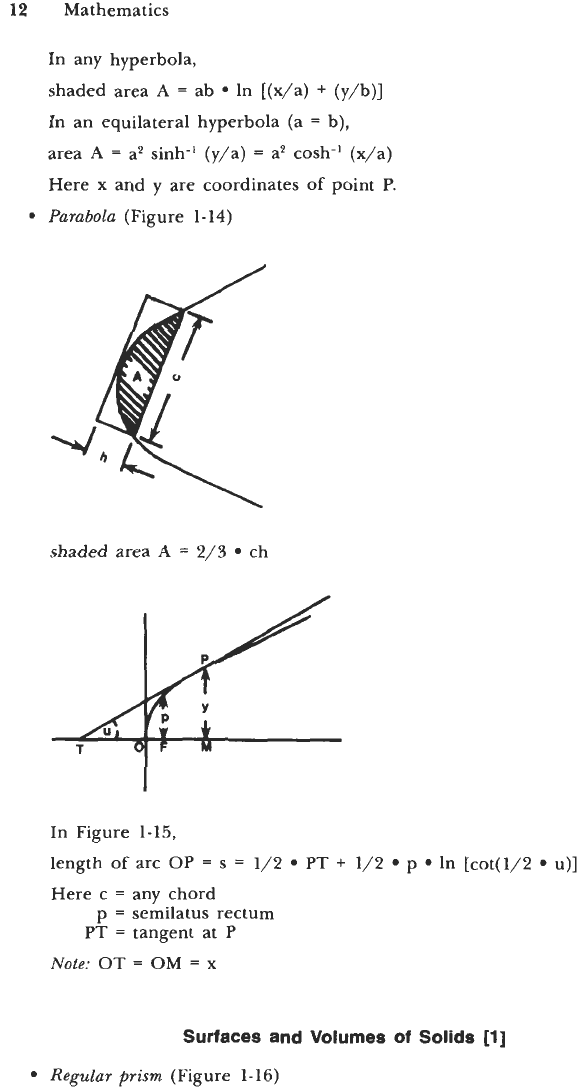
12
Mathematics
In any hyperbola,
shaded area
A
=
ab In [(x/a)
+
(y/b)]
In an equilateral hyperbola (a
=
b),
area
A
=
a2 sinh-’ (y/a)
=
a2 cosh-’ (x/a)
Here
x
and
y
are coordinates
of
point
P.
Parabola
(Figure 1-14)
shaded area
A
=
2/3
ch
In Figure 1-15,
length
of
arc
OP
=
s
=
1/2 PT
+
1/2
p In [cot(1/2 u)]
Here c
=
any chord
p
=
semilatus rectum
PT
=
tangent at
P
Note:
OT
=
OM
=
x
Surfaces
and
Volumes
of
Solids
[I]
Regular
prism
(Figure 1-16)
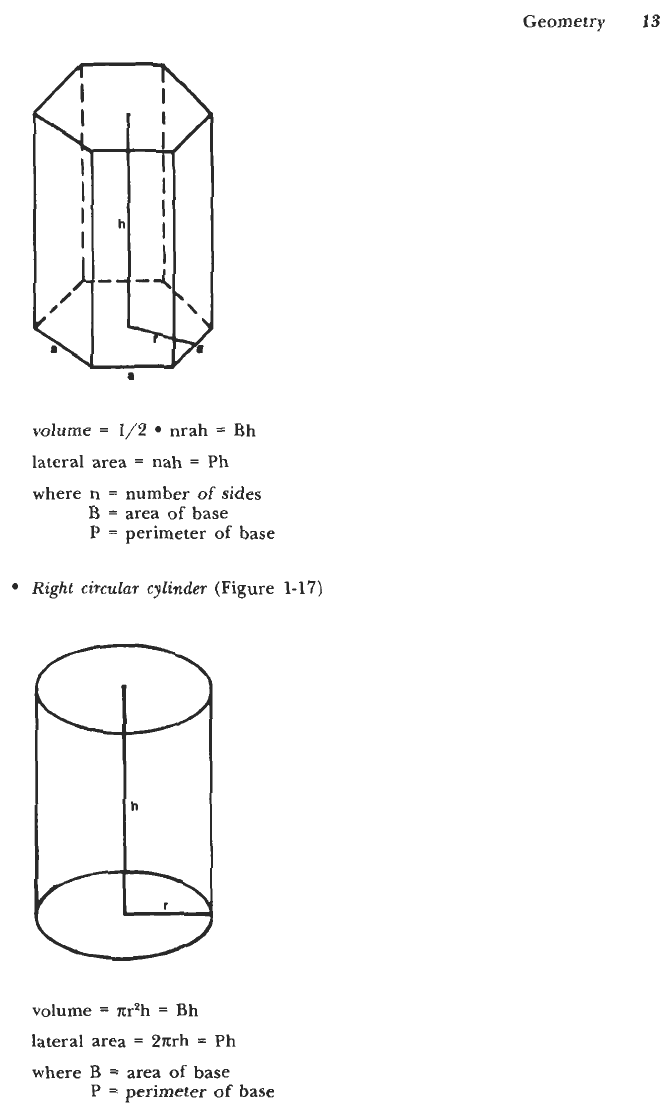
Geometry
13
volume
=
1/2
nrah
=
Bh
lateral area
=
nah
=
Ph
where
n
=
number
of
sides
B
=
area
of
base
P
=
perimeter
of
base
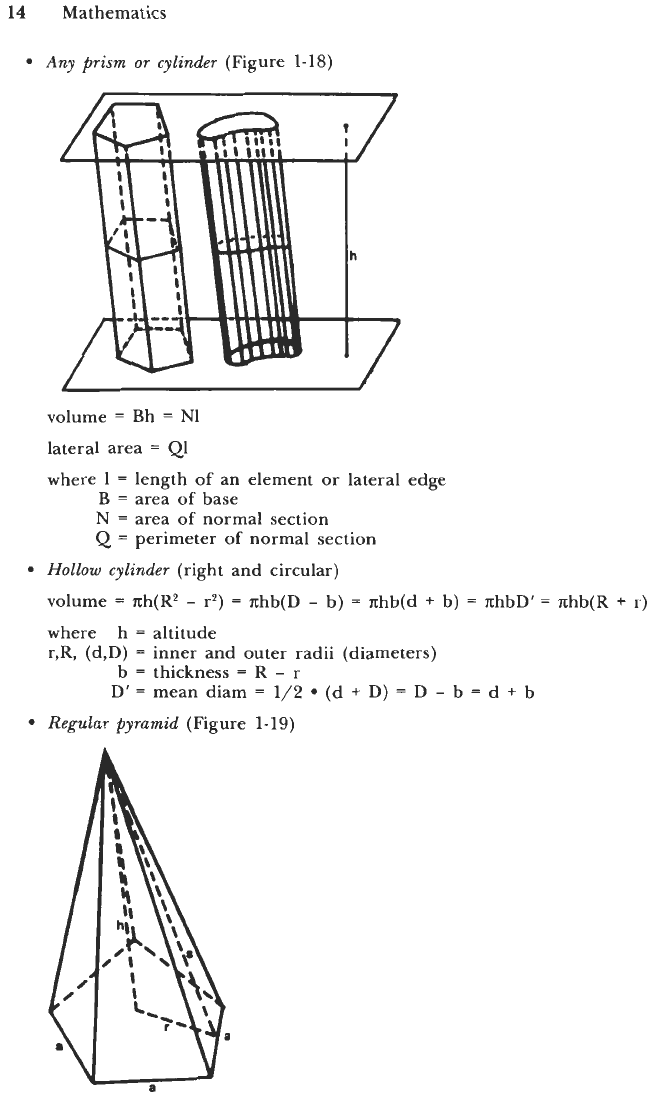
Right
circular cylinder
(Figure
1-17)
h
volume
=
nreh
=
Bh
lateral area
=
2nrh
=
Ph
where B
=
area
of
base
P
=
perimeter
of
base
14
Mathematics
.
Any prism
or
cylinder
(Figure
1-18)
,
volume
=
Bh
=
N1
lateral area
=
Q1
where
1
=
length
of
an element or lateral edge
B
=
area
of
base
N
=
area
of
normal section
Q
=
perimeter
of
normal section
Hollow
cylinder
(right and circular)
volume
=
rch(R2
-
r2)
=
nhb(D
-
b)
=
nhb(d
+
b)
=
rchbD'
=
rchb(R
+
r)
where h
=
altitude
r,R, (d,D)
=
inner and outer radii (diameters)
b
=
thickness
=
R
-
r
D'
=
mean diam
=
1/2
(d
+
D)
=
D
-
b
=
d
+
b
Regular pyramid
(Figure
1-19)
