Lyons W.C. (ed.). Standard handbook of petroleum and natural gas engineering.2001- Volume 1
Подождите немного. Документ загружается.


Analytic Geometry
55
Polar equation (focus as origin)
r
=
p/(l
-
e cos
e)
Equation of the tangent at (xI,yI)
b2xlx
+
a2y,y
=
a2b2
Equations
of
a Hyperbola (Figure
1-42)
(x-h)' (Y-k)'
0
---=I
a2 b2
Coordinates of the center C(h,k), of vertices V(h
+
a,k) and V'(h
-
a,k),
and of the foci F(h
+
ae,k) and F'(h
-
ae,k)
Center at origin
x2/a2
-
y2/b2
=
1
Equation of the directrices
x
=
h
*
a/e
Equation of the asymptotes
y
-
k
=
k
b/a (x
-
k)
Equation
of
the eccentricity
da2
+
b2
,
e=
Length of the latus rectum
LL'
=
2b2/a
Parametric form, replacing x and
y
x
=
a cosh u and
y
=
b sinh u
Polar equation (focus as origin)
r
=
p/(1
-
e cos
e)
a
Y
Figure
1-42.
Equation
of
a
hyperbola.

56
Mathematics
Equation of the tangent at (x,y)
b2x,x
-
a2y,y
=
a2b2
Equations
of
Three-Dimensional Coordinate Systems (Figure
1-43)
Distance
d
between two points
d
=
J(x,
-
x1
1'
+
(y,
-
yl
1'
+
(~2
-
~1
1'
Direction cosines of a line
h
=
cos
a,
p
=
cos
p,
v
=
cos
y
Direction numbers, proportional to the direction cosines with
k
a
=
kh,
b
=
kp,
c
=
kv
Equations
of
a Plane
ax+by+cz+d=O
Intercept
x/a
+
y/b
+
z/c
=
1
Normal form
hx
+
py
+
vz
-
p
=
0
Distance from
ax
+
by
+
cz
+
d
=
0
to a point P(x,,y,,z,)
ax,+by,+c,+d
V
Figure
1-43.
Three-dimensional coordinate systems.

Analytic Geometry
57
Equations of a Line
Intersection of two planes
alx
+
bly
+
cIz
+
d,
=
0
i
apx
+
b,y
+
c,z
+
x,
=
0
For this line
Symmetric form, Le., through (x,,yI,zI) with direction numbers a, b, and c
(x
-
xJ/a
=
(y
-
YJ/b
=
(z
-
z,)/c
Through two points
x--1
-
Y-Y1
-
Z-Z1
X2-Xx1
YZ-YI
22-21
where
h:p:v
=
(xp
-
xI):(y2
-
y1):(z2
-
zl)
Equations of Angles
Between two lines
cos
e
=
h,h,
+
plp2
+
vIv2
and the lines are parallel if cos
8
=
1
or perpendicular if cos
8
=
0
Between two planes, given by the angle between the normals
to
the planes.
Equation (standard form)
of
a Sphere (Figure 1-44)
x‘L
+
y2
+
22
=
r
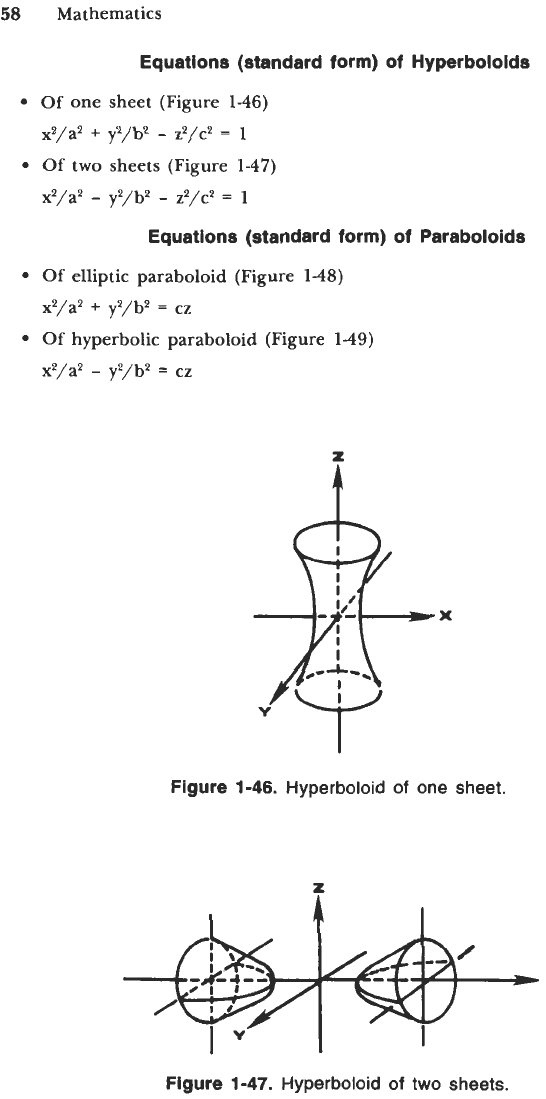
Equation (standard form) of an Ellipsoid (Figure 1-45)
V-
Figure 1-44. Sphere.
V
Figure 1-45. Equation
of
an
ellipsoid.
58
Mathematics
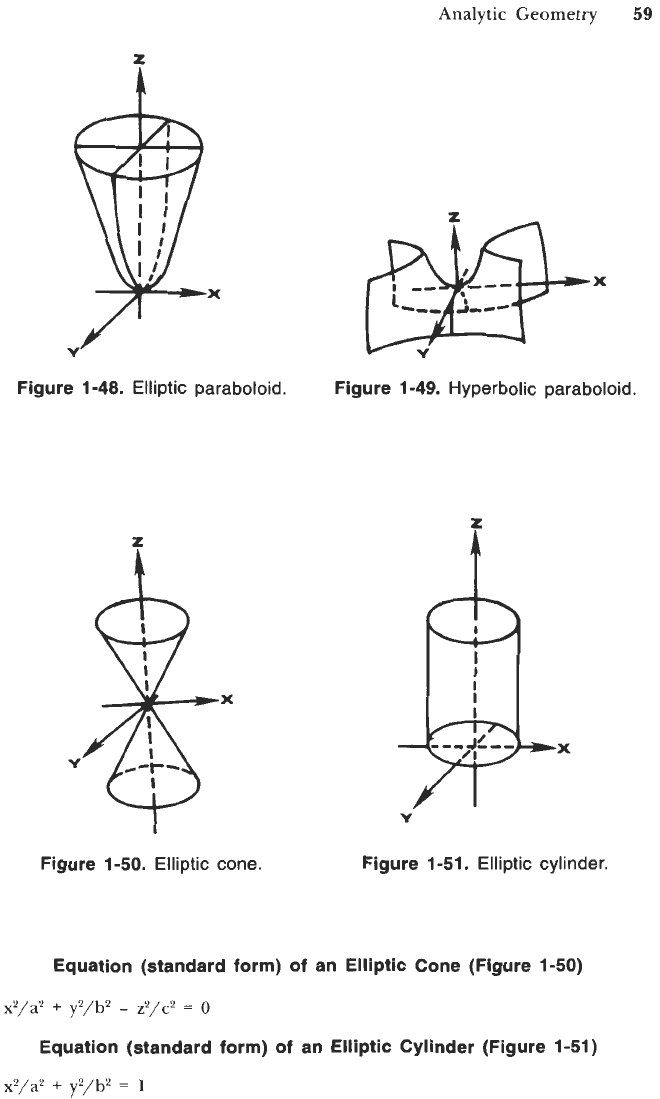
Equations (standard form) of Hyperboloids
Of
one sheet (Figure
1-46)
x2/a2
+
y2/b2
-
z2/c2
=
1
Of
two sheets (Figure
1-47)
x2/a2
-
y2/b2
-
z2/c2
=
1
Equations (standard form) of Paraboloids
Of
elliptic paraboloid (Figure 1-48)
x2/a2
+
y2/b2
=
cz
Of
hyperbolic paraboloid (Figure
1-49)
x2/a2
-
y2/b2
=
cz
Figure
1-46.
Hyperboloid
of
one
sheet.
Figure
1-47.
Hyperboloid
of
two sheets.
Analytic Geometry
59
Figure 1-48.
Elliptic paraboloid.
Figure 1-49.
Hyperbolic paraboloid.
Figure 1-50.
Elliptic cone.
p
--..J/---
/I
X
V
Figure 1-51.
Elliptic cylinder.
Equation (standard form) of an Elliptic Cone (Figure 1-50)
$/a2
+
y2/b2
-
z'/c'
=
0
Equation (standard form) of an Elliptic Cylinder (Figure 1-51)
x?/a(L
+
y2/b2
=
1

60
Mathematics
NUMERICAL METHODS
See References
1
and
9-22
for additional information.
Expansion in Series
If
the value of a function f(x) can be expressed in the region close to x
=
a,
and if all derivatives of f(x) near a exist and are finite, then by the infinite
power series
(x
-
a)"
f"(a)+
. . .
f(x)=f(a)+(x-a)f'(a)+- f"(a)+
. . .
+-
(x
-
a)'
2!
n!
and f(x) is
analytic
near
x
=
a. The preceding power series is called the
Taylor
series expansion
of f(x) near x
=
a.
If
for some value of x as [x
-
a] is increased,
then the series is no longer convergent, then that value of x is outside the radius
of convergence of the series.
The error due to truncation of the series is partially due to [x
-
a] and
partially due to the number of terms (n) to which the series is taken. The
quantities [x
-
a] and n can be controlled and the truncation error is said to
be of the order of
(x
-
a)"+I or O(x
-
a)"".
Finite Difference Calculus
In the finite difference calculus, the fundamental rules of ordinary calculus
are employed, but Ax is treated as a small quantity, rather than infinitesimal.
Given a function f(x) which is analytic (i.e., can be expanded in
a
Taylor series)
in the region of a point x, where h
=
Ax, if f(x
+
h) is expanded about x, f'(x)
can be defined at x
=
xi as
f'(xi)
=
f;
=
(f,+,
-
fi)/h
+
O(h)
The first
forward difference
of
f
at xi may be written as
Afi
=
fi+l
-
fi
and then
f'(x)
=
(Af,)/h
+
O(h)
The first
backward difference
of
f
at xi is
Vf,
=
fi
-
fi-l
and f'(x) may also be written
as
f'(x)
=
(Vfi)/h
+
O(h)

Numerical Methods
61
The second forward difference of f(x) at
xi
is
A*fi
=
fi+'
-
2fi+,
+
f,
and the second derivative of f(x) is then given by
f"(x)
=
(A2fi)/h2
+
O(h)
The second backward difference of
f
at xI is
V'f,
=
f,
-
2f
3-1
+
f,-2
and f"(x) may also be defined as
f"(x)
=
(V2f,)/h2
+
O(h)
Approximate expressions for derivatives of any order are given in terms of
forward and backward difference expressions as
fb)
=
(A"f,)/h"
+
O(h)
=
(V"f,)/h"
+
O(h)
Coefficients of forward difference expressions for derivatives of up to the
fourth order are given in Figure 1-52 and of backward difference expressions
in Figure 1-53.
More accurate difference expressions may be found by expanding the Taylor
series. For example, f'(x) to V(h) is given by forward difference by
f'(x)
=
(-fi+,
+
4fi+,
-
3fi)/(2h)
+
O(h2)
and a similar backward difference representation can also be easily obtained.
These expressions are exact for a parabola. Forward and backward difference
expressions of O(h2) are contained in Figures 1-54 and 1-55.
A
central
difference
expression may be derived by combining the equations for
forward and backward differences.
__
~~~
Figure
1-52.
Forward difference coefficients
of
o(h).

62
Mathematics
I
I
I
+
6(b)
I
I
fi
I
IU'(xi)
=I
I
I
1-11 1
I
IhY"(xi)
=I I
Ill-21
1
I
Ih'f'''(Xi)
51
1-11
3131
1
I
I
fi-4
I
fta
I
fi-a
I
fti
I
(Xi)=I
1
I
-4
I
6
I
-4
I
1
I
(h4f'
@
#
e
Figure
1-53. Backward difference coefficients
of
o(h).
Figure
1-54. Forward difference coefficients
of
o(h)2.
Figure
1-55. Backward difference coefficients
of
o(h)*.

Numerical Methods
63
Sf,
=
1/2
(Af,
+
Vf,)
=
1/2 (fi+,
-
f,.,)
The first derivative off at x, may then be given in terms of the central difference
expression as
f',
=
(6f,)/h
+
O(hz)
and is accurate to a greater degree than the forward or backward expressions
of
f'.
Central difference expressions for derivatives of any order in terms of
forward and backward differences are given by
f:")
=
[Vnfi+"/*
+
A"fi_,,,]/(2h")
+
O(h2), n even
and
f:")
=
[Vnf,+(n.1)/2
+
A"fi.(n_,,zl/(2h")
+
O(h2), n odd
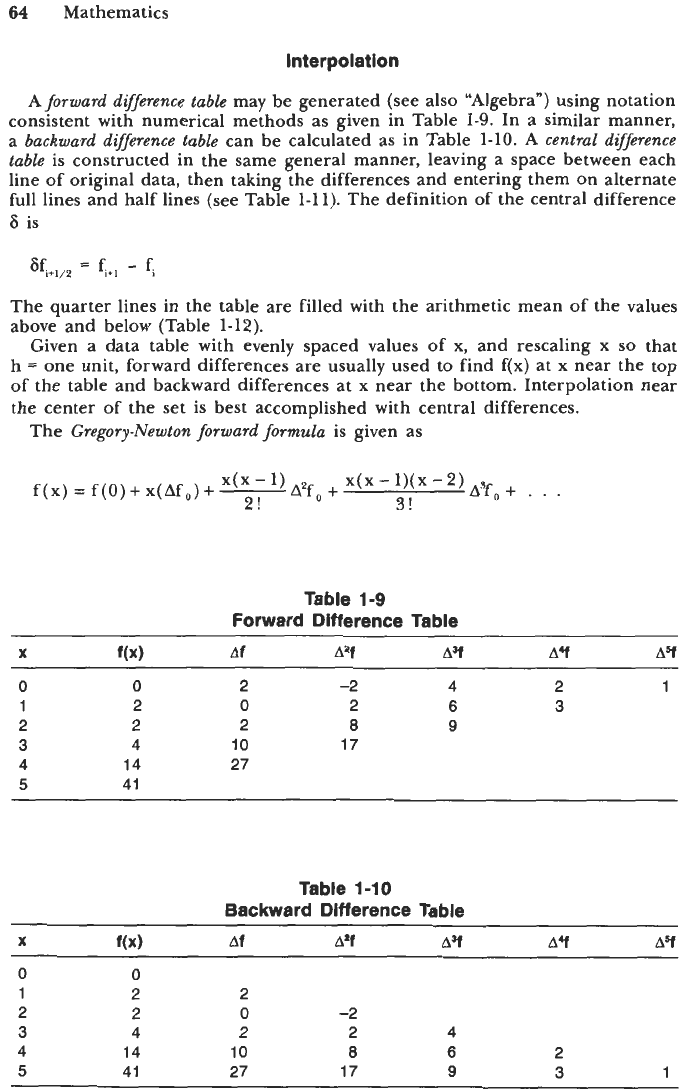
Coefficients of central difference expressions for derivatives up to order four
of O(h2) are given in Figure 1-56 and of O(h4) in Figure 1-57.
-
Figure
1-56.
Central difference coefficients
of
o(h)2.
Figure
1-57.
Central difference coefficients
of
~(h)~
64
Mathematics
Interpolation
A
forward difference table
may be generated (see also "Algebra") using notation
consistent with numerical methods as given in Table 1-9. In a similar manner,
a
backward difference table
can be calculated as in Table 1-10.
A
central difference
table
is constructed in the same general manner, leaving a space between each
line of original data, then taking the differences and entering them on alternate
full lines and half lines (see Table 1-11). The definition of the central difference
6
is
6fi+l,p
=
fi+,
-
fi
The quarter lines in the table are filled with the arithmetic mean of the values
above and below (Table 1-12).
Given a data table with evenly spaced values of x, and rescaling x
so
that
h
=
one unit, forward differences are usually used to find f(x) at x near the top
of the table and backward differences at x near the bottom. Interpolation near
the center of the set is best accomplished with central differences.
The
Gregory-Newton forward formula
is given as
x(x-l)(x-2)
5
ATo
+
&f,+
. .
.
x(x
-
1)
f(x) =f(O)+x(Af,)+-
2!
3!
Table
1-9
Forward Difference Table
X
foo
Af A2f AJf AY AY
0
0
2 -2 4 2 1
1 2
0
2
6
3
2 2 2
8
9
3
4
10
17
4 14 27
5
41
Table
1-10
Backward Difference Table
0
0
1
2
2
2
2
0
-2
3
4 2 2 4
4 14 10
8
6
2
5
41 27 17
9
3
1
