Lyons W.C. (ed.). Standard handbook of petroleum and natural gas engineering.2001- Volume 1
Подождите немного. Документ загружается.

Numerical Methods
65
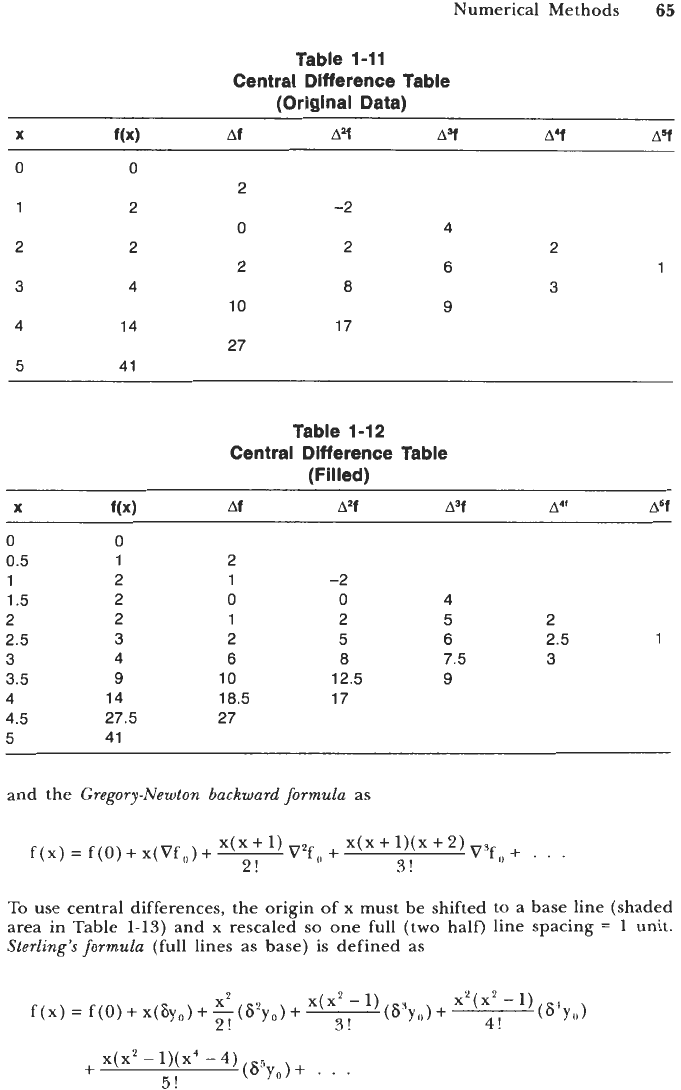
Table
1-11
Central Difference Table
(Original Data)
X
f(x)
Af A2f AY AV Asf
0
0
1 2 -2
2 2 2 2
3 4 8 3
4 14 17
5 41
2
0
4
2
6
1
10
9
27
Table
1-12
Central Difference Table
(Filled)
X
f(x) Af A2f A3f Ad' A5f
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
0
1
2
2
2
3
4
9
14
27.5
41
2
1 -2
0
0
4
1 2 5 2
2 5
6
2.5
1
6
8 7.5 3
10 12.5
9
18.5 17
27
and the
Gregory-Newton
backward formula
as
...
f(x)
=
f(O)+x(Vf,,)+- x(x
+
1)
VZf,,
+
x(x
+
l)(x
+
2)
VSf,,
+
2!
3!
To
use central differences, the origin of x must be shifted to a base line (shaded
area in Table 1-13) and x rescaled
so
one full (two half) line spacing
=
1
unit.
Sterling's
formula
(full lines as base) is defined as
4)(6"")+
.
x(x*
-
1)(x4
-
+
5!

66
Mathematics
Table 1-13
Central Difference Table with Base Line
Old
x
New
x
f(x)
Af
A2f
A3f
A9
AY
0
-2.5
0
0.5 -2.0 1 2
1 -1.5 2 1 -2
1.5 -1
.o
2
0 0
4
2 -0.5 2 1 2 5 2
3
+0.5
4
6
8 7.5
3
3.5 +1
.o
9
10 12.5
9
4
+1.5 14 18.5 17
4.5 +2.0 27.5 27
5 +2.5 41
and
Bessel's formula
(half line as base) as
f(x)
=
f(O)+x(6y1,)
=
(x2
-
3
(62yo)
+
X(X2
-
+I
2!
3!
(
x2
-t)(
x2
-
4)
.(
x2
-+)(
x2
-
4)
(65yo)+
. . .
5!
+
(6
YO)+
4!
Interpolation with nonequally spaced data
may
be accomplished by the use of
Lagrange Polynomials,
defined as a set of nth degree polynomials such that each
one, PAX)
(j
=
0,
1,
. .
.,
n), passes through zero at each of the data points except
one, xt, where
k
=
j.
For
each polynomial in the set
where if
then

Numerical Methods
67
and the linear combination of Pj(x) may be formed
It can be seen that for any xi, p,(xi)
=
f(xi).
Interpolation
of
this type may be extremely unreliable toward the center
of
the region where the independent variable is widely spaced. If it is possible
to
select the values of
x
for which values of f(x)
will
be obtained, the maximum
error can be minimized by the proper choices. In this particular case Chebyshev
polynomials can be computed and interpolated
[ll].
Neville’s algorithm
constructs the same unique interpolating polynomial and
improves the straightforward Lagrange implementation by the addition of an
error estimate.
If Pi(i
=
1,
. .
.,n) is defined as the value at x of the unique polynomial of
degree zero passing through the point (xi,yi) and Pi. (i
=
1,
.
.
.,
n
-
1,
j
=
2,
. .
.,
n)
the polynomial of degree one passing through 60th (xi,yi) and (x.,~.), then the
higher-order polynomials may likewise be defined up to
PIPB,,,n,
which
is
the value
of
the unique interpolating polynomial passing through all n points.
A
table
may be constructed, e.g.,
if
n
=
3
Neville’s algorithm recursively calculates the preceding columns from left to
right as
In addition the differences between the columns may be calculated as
and
the rightmost member of the table
[22].
rational functions
of
the general form
is equal to the sum of any
yi
plus a set of
C’s
and/or
D’s
that lead to
Functions with localized strong inflections or poles may be approximated by

68
Mathematics
as long as there are sufficient powers of x in the denominator to cancel any
nearby poles. Bulirsch and Stoer [16] give a Neville-type algorithm that performs
rational function extrapolation on tabulated data
starting with
Ri
=
yi
and returning an estimate of error, calculated by
C
and
D
in a manner analogous with Neville’s algorithm for polynomial approximation.
In a high-order polynomial, the highly inflected character of the function
can more accurately be reproduced by the
cubic spline function.
Given a series
of xi(i
=
0,
1,
. .
.,
n) and corresponding f(xi), consider that for two arbitrary
and adjacent points xi and xi+j, the cubic fitting these points is
Fi(x)
=
a,
+
aix
+
a2x2
+
a,x3
(x,
I
x
I
Xi+J
The approximating cubic spline function g(x) for the region (xo
I
x
I
xn) is
constructed by matching the first and second derivatives (slope and curvature)
of Fi(x) to those of Fi-l(x), with special treatment (outlined below) at the end
points,
so
that g(x) is the set of cubics Fi(x),
i
=
0, 1, 2,
.
.
,,
n
-
1, and the
second derivative g“(x) is continuous over the region. The second derivative
varies linearly over [x,,xn] and at any x
(x,
5
x
I
x,+,)
x
-
x,
X~+I
-
Xi
g”(
x)
=
g”( x,
)
+
-
[g”(xi+l)
-
g”(x,
)I
Integrating twice and setting g(xi)
=
f(xi) and g(xCl)
=
f(xi+l), then using the
derivative matching conditions
Fi(xi)
=
F;+,(xi) and F:(xi)
=
FY-l(xi)
and applying the condition for
i
=
[l, n
-
11 finally yields
a
set of linear
simultaneous equations of the form

Numerical Methods
69
where
i
=
1, 2,
. .
.,
n
-
I
Axi
=
xi+,
-
xi
If the xl are equally spaced by Ax, then the preceding equation becomes
There are n
-
1
equations in n
+
1 unknowns and the two necessary additional
equations are usually obtained by setting
g”(x,)
=
0
and g”(x,)
=
0
and g(x) is now referred to as a
natural cubic spline.
g”(x,,) or g”(x,) may alternatively
be set to values calculated
so
as to make g’ have a specified value on either or
both boundaries. The cubic appropriate for the interval in which the x value
lies may now be calculated (see “Solutions of Simultaneous Linear Equations”).
Extrapolation
is required if f(x) is known on the interval [a,b], but values
of
f(x) are needed for
x
values not in the interval. In addition
to
the uncertainties
of interpolation, extrapolation is further complicated since the function is fixed
only on one side. Gregory-Newton and Lagrange formulas may be used for
extrapolation (depending on the spacing of the data points), but all results
should be viewed with extreme skepticism.
Roots
of
Equations
Finding the root of an equation in x is the problem of determining the values
of
x
for which f(x)
=
0.
Bisection,
although rarely used now, is the basis of several
more efficient methods. If a function f(x) has one and only one root in [a,b],
then the interval may be bisected at
xm
=
(a
+
b)/2. If f(xm) f(b)
<
0,
the root
is in [x,,b], while if f(x,)
f(b)
>
0,
the root is in [a,xm]. Bisection of the
appropriate intervals, where
XI
=
(a‘
+
b’)/2,
is
repeated until the root is located
f
E,
E
being the maximum acceptable error and
E
I
1/2 size of interval.
The
Regula
Falsa
method
is a refinement of the bisection method, in which
the new end point of a new interval is calculated from the old end points by
Whether xm replaces a or replaces b depends again on the sign of a product, thus
if f(a)
f(xm)
<
0,
then the new interval is [a,xm]
or
if f(x,)
f(b)
<
0,
then the new interval is [x,,b]

70
Mathematics
Because of round off errors, the Regula Falsa method should include a check
for excessive iterations. A
modified Regula FaLsa method
is based on the use
of
a
relaxationfactor,
Le., a number used to alter the results of one iteration before
inserting into the next. (See the section on relaxation methods and "Solution
of Sets of Simultaneous Linear Equations.")
By iteration, the general expression for the
Newton-Raphson method
may be
written
(if
f'
can be evaluated and is continuous near the root):
where (n) denotes values obtained on the nth iteration and (n
+
1)
those obtained
on the (n
+
l)lh
iteration. The iterations are terminated when the magnitude of
16("+')
-
6(")1
<
E,
being the predetermined error factor and
E
s
0.1
of the
permissible error in the root.
The
modified Newton method
[
121
offers one way of dealing with multiple roots.
If a new function is defined
since u(x)
=
0
when f(x)
=
0
and if f(x) has a multiple root at
x
=
c of multiplicity
r, then Newton's method can be applied and
where
f
(x)f"( x)
[f'(x)I2
u'(x)
=
1
-
If multiple
or
closely spaced roots exist, both
f
and
f'
may vanish near a root
and therefore methods that depend on tangents
will
not work. Deflation of the
polynomial P(x) produces, by factoring,
where Q(x) is a polynomial of one degree lower than P(x) and the roots of
Q
are the remaining roots of P after factorization by synthetic division. Deflation
avoids convergence to the same root more than one time. Although the cal-
culated roots become progressively more inaccurate, errors may be minimized
by using the results as initial guesses to iterate for the actual roots in
P.
Methods such as Graeffe's root-squaring method, Muller's method, Laguerre's
method, and others exist for finding all roots of polynomials with real coeffi-
cients.
[12
and others]

Numerical Methods
71
Solution
of
Sets
of
Simultaneous Linear Equations
A matrix is a rectangular array of numbers, its size being determined by the
number of rows and columns in the array. In this context, the primary concern
is with square matrices, and matrices of column dimension
1
(column vectors)
and row dimension
1
(row vectors).
Certain configurations of square matrices are of particular interest. If
the diagonal consisting of cl,, cz2, c33 and cqq is the
main diagonal.
The matrix
is
symmetric
if
c
=
c,,. If all elements below the main diagonal are zero (blank), it
is an
upper t&ngular matrix,
while if all elements above the main diagonal are
zero, it is a
lower triangular matrix.
If all elements are zero except those on the
main diagonal, the matrix is a
diagonal matrix
and if a diagonal matrix has all
ones on the diagonal,
it
is the
unit, or identity, matrix.
Matrix addition (or subtraction) is denoted as S
=
A
+
B and defined as
s.
=
a,.
+
b.
II
?I
'J
where A. B, and
S
have identical row and column dimensions. Also,
A+B=B+A
A-B=-B+A
Matrix multiplication, represented as
P
=
AB, is defined as
where n is the column dimension of A and the row dimension of B.
P
will have
row dimension of A and column dimension of B. Also
AI
=
A
and
IA
=
A
while, in general,
AB
#
BA
Matrix division is not defined, although if
C
is a square matrix,
C-'
(the
inverse
of C) can usually be defined
so
that
CC-'
=
I

72
Mathematics
and
The
transpose
of A
if
is
A square matrix
C
is
orthogonal
if
The
determinant
of a square matrix
C
(det
C)
is defined as the sum of all
possible products found by taking one element from each row in order from
the top and one element from each column, the sign of each product multiplied
by
(-ly,
where r is the number of times the column index decreases in the product.
For a
2
x
2
matrix
det
C
=
cllcpB
-
c12c21
(Also see discussion of determinants in “Algebra.”)
unknowns:
Given a set of simultaneous equations, for example, four equations in four

Numerical Methods
73
x1
x2
XS
x4
or
rl
=
r2
rs
r4
CX
=
R
1
c:,
c;,
c;,
‘21
‘22
‘25
‘24
‘91
‘32
‘35
‘34
‘41
‘42
‘45
‘44
The solution for xk in a system of equations such as given in the matrix above
is
x1
rI
=
‘2
xS
‘3
x4 ‘4
xk
=
(det C,)/(det C)
where C, is the matrix C, with its
kth
column replaced by
R
(Cramer’s Rule).
If
det C
=
0,
C and its equations are singular and there is no solution.
Sets of simultaneous linear equations are frequently defined as
[
121:
Sparse
(many zero elements) and large
Dense
(few zero elements) and small.
A
banded matrix
has all zero elements
except for a band centered on the main diagonal, e.g.,
then C is a banded matrix of bandwidth
3,
also called a
tridiugonal matrix.
Equation-solving techniques may be defined as
direct,
expected to yield results
in a predictable number of operations,
or
iterative,
yielding results of increasing
accuracy with increasing numbers of iterations. Iterative techniques are in
general preferable for very large sets and for large, sparse (not banded) sets.
Direct methods are usually more suitable for small, dense sets and also for sets
having banded coefficient matrices.
Gauss
elimination
is the sequential application of the two operations:
1.
Multiplication,
or
division, of any equation by a constant.
2.
Replacement of an equation by the sum,
or
difference, of that equation
and any other equation in the set,
so
that a set of equations
‘11
‘12
‘19
‘14
‘21
‘22
‘25
‘24
‘31
‘32
‘83
‘34
‘41
‘42
‘43
‘44

74
Mathematics
then, by replacement of the next three equations,
and finally
Gauss-Jordan
elimination is a variation of the preceding method, which by
continuation of the same procedures yields
Therefore, x,
=
r,",
etc., Le., the r vector is the solution vector. If the element
in the current pivot position is zero or very small, switch the position of the
entire pivot row with any row below it, including the
x
vector element, but not
the r vector element.
If det
C
#
0,
C-'
exists and can be found by
matrix
inversion
(a modification
of the Gauss-Jordan method), by writing
C
and
I
(the identity matrix) and then
performing the same operations on each to transform
C
into I and, therefore,
I into
C-I.
If a matrix is ill-conditioned, its inverse may be inaccurate or the solution
vector for its set of equations may be inaccurate. Two of the many ways to
recognize possible ill-conditioning are
1.
If there are elements of the inverse of the matrix that are larger than
2.
If the magnitude of the determinant is small, i.e.,
if
elements of the original matrix.
det
C
,-
5
1
Gauss-Siedel method
is an iterative technique for the solution of sets of equa-
tions. Given, for example, a set of three linear equations
