Lyons W.C. (ed.). Standard handbook of petroleum and natural gas engineering.2001- Volume 1
Подождите немного. Документ загружается.


Applied Statistics
95
The
normal (Gaussian) distribution
is the most frequently used probability
function and
is
given by
where y
=
location parameter
o
=
scale parameter
The cumulative function for this distribution is ff(X).
z
where
The
standard normal distribution
is determined by calculating a random variable
z
=
(X
-
y)/o
for the population
z
=
(X
-
x)/S
for the sample
The probability function for the standard normal distribution is then
where
z
has a mean of zero and a standard deviation of one. Probability
estimates are evaluated by integrating
f(z)
The
t
(Student’s
t)
distribution
is an unbounded distribution where the mean
is zero and the variance is
v/(v
-
2),
v
being the scale parameter (also called
“degrees of freedom”). As
v
-+
00,
the variance
+
1
(standard normal distribu-
tion).
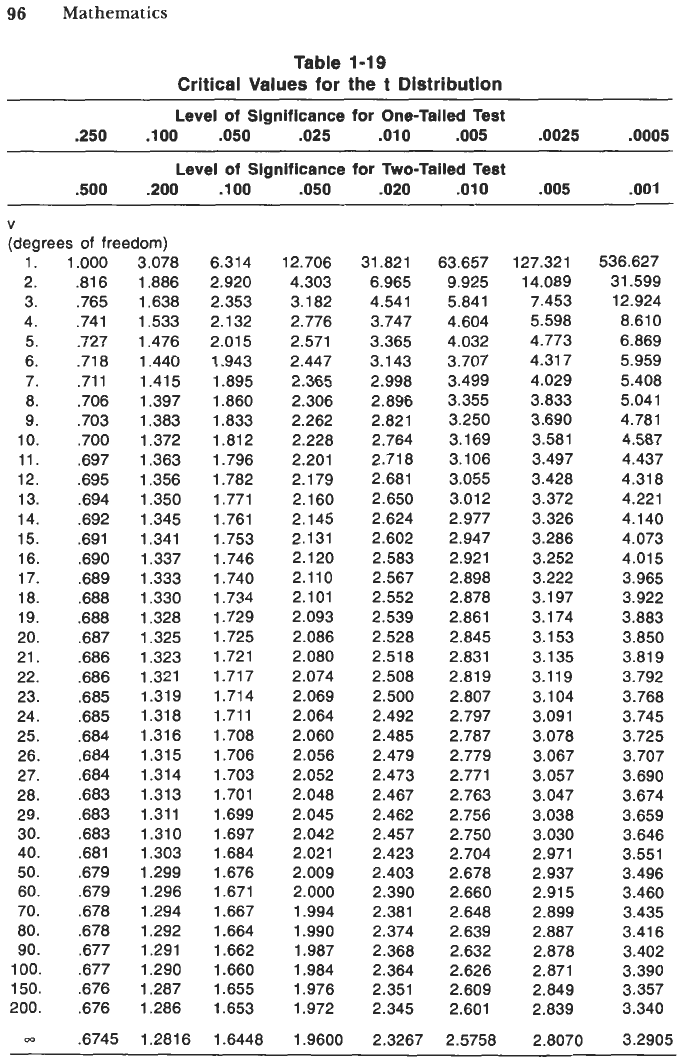
A
t table such as Table 1-19 is used to find values of the
t
statistic where
v
is located along the vertical margin and the probability is given on the
horizontal margin. (For a one-tailed test, given the probability for the left tail,
the t value must be preceded by a negative sign.)
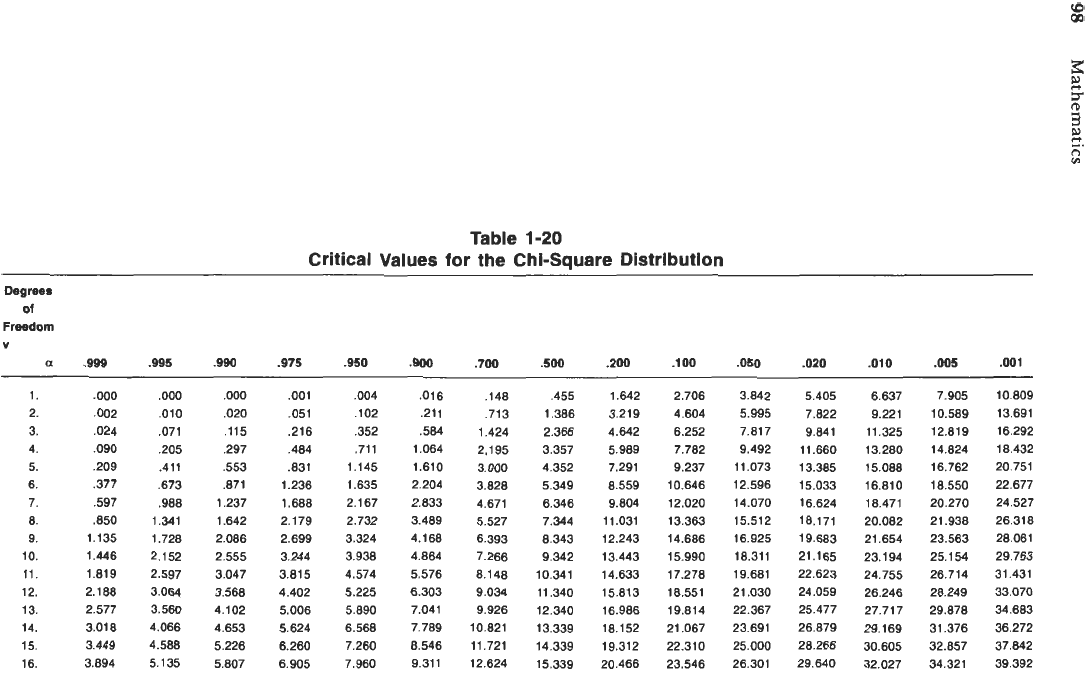
The
chi-square distribution
gives the probability for a continuous random
variable bounded on the left tail. The probability function has a shape parameter
v
(degrees of freedom), a mean of v, and a variance of 2v. Values of the
X2
characteristic are obtained from a table such as Table
1-20,
which is of similar
construction as the t table (Table 1-19).
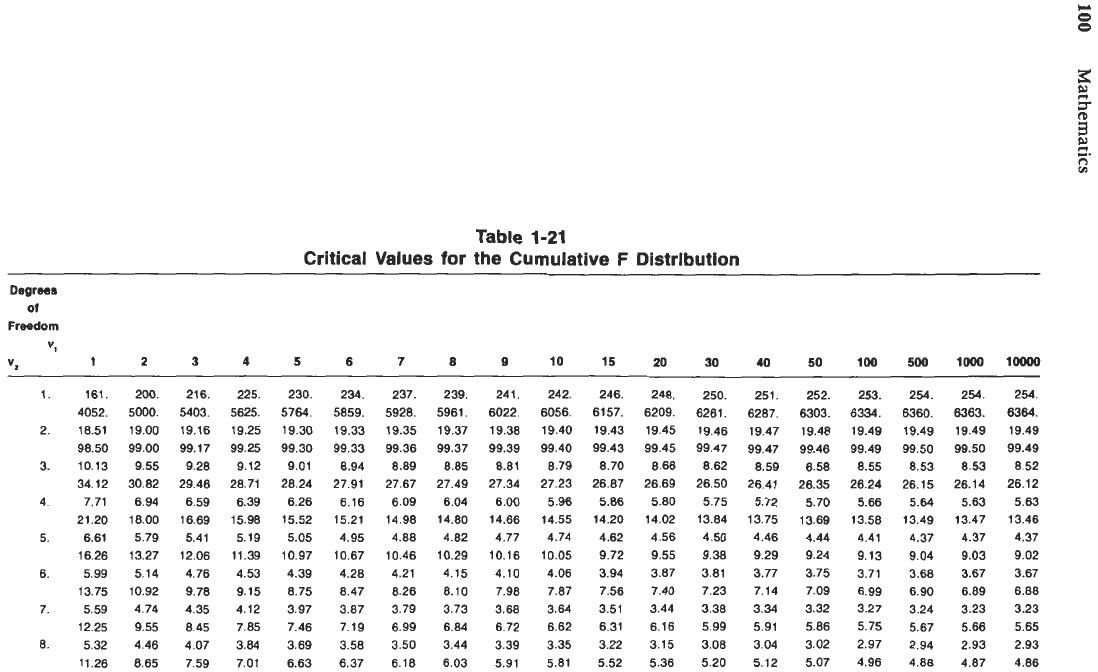
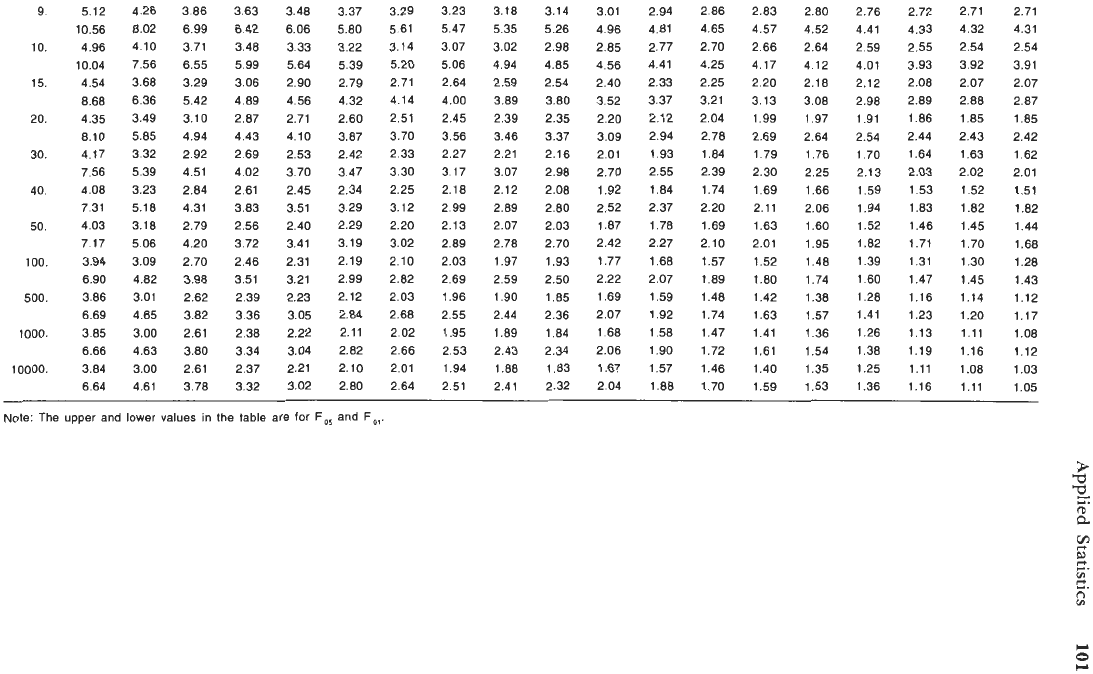
The
F
distribution
has two shape parameters,
v,
and
v2.
Table 1-21 shows
F
values
for 1% and
5%
probabilities.
Note: F(v,,v,)
f
F(v,,v,)
96
Mathematics
Table
1-19
Critical Values for the t Distribution
Level of Significance for One-Tailed Test
.250
.lo0
.050
.025
.010
.005
.0025
.0005
Level
of
Significance for Two-Tailed Test
.500
.200
.lo0
.os0
.020
.010
.005
.001
V
(degrees
of
freedom)
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
40.
50.
60.
70.
80.
90.
100.
150.
200.
m
1.000
3.078
.816 1.886
.765 1.638
,741 1.533
.727 1.476
,718 1.440
,711 1.415
.706 1.397
,703 1.383
.700 1.372
,697 1.363
,695 1.356
,694 1.350
,692 1.345
,691 1.341
.690 1.337
,689 1.333
,688 1.330
.688 1.328
,687 1.325
.686 1.323
.686 1.321
,685 1.319
,685 1.318
.684 1.316
,684 1.315
.684 1.314
,683 1.313
.683 1.311
.683 1.310
.681 1.303
.679 1.299
.679 1.296
,678 1.294
.678 1.292
.677 1.291
.677 1.290
,676 1.287
,676 1.286
6.314
2.920
2.353
2.132
2.015
1.943
1.895
1.860
1.833
1.812
1.796
1.782
1.771
1.761
1.753
1.746
1.740
1.734
1.729
1.725
1.721
1.717
1.714
1.71
1
1.708
1.706
1.703
1.701
1.699
1.697
1.684
1.676
1.671
1.667
1.664
1.662
1.660
1.655
1.653
12.706
4.303
3.182
2.776
2.571
2.447
2.365
2.306
2.262
2.228
2.201
2.179
2.160
2.145
2.131
2.120
2.110
2.101
2.093
2.086
2.080
2.074
2.069
2.064
2.060
2.056
2.052
2.048
2.045
2.042
2.021
2.009
2.000
1.994
1.990
1.987
1.984
1.976
1.972
31.821
6.965
4.541
3.747
3.365
3.143
2.998
2.896
2.821
2.764
2.718
2.681
2.650
2.624
2.602
2.583
2.567
2.552
2.539
2.528
2.518
2.508
2.500
2.492
2.485
2.479
2.473
2.467
2.462
2.457
2.423
2.403
2.390
2.381
2.374
2.368
2.364
2.351
2.345
63.657
9.925
5.841
4.604
4.032
3.707
3.499
3.355
3.250
3.169
3.106
3.055
3.012
2.977
2.947
2.921
2.898
2.878
2.861
2.845
2.831
2.81 9
2.807
2.797
2.787
2.779
2.771
2.763
2.756
2.750
2.704
2.678
2.660
2.648
2.639
2.632
2.626
2.609
2.601
.6745 1.2816 1.6448 1.9600 2.3267 2.5758
127.321
14.089
7.453
5.598
4.773
4.317
4.029
3.833
3.690
3.581
3.497
3.428
3.372
3.326
3.286
3.252
3.222
3.197
3.174
3.153
3.135
3.119
3.104
3.091
3.078
3.067
3.057
3.047
3.038
3.030
2.971
2.937
2.91 5
2.899
2.887
2.878
2.871
2.849
2.839
2.8070
536.627
31.599
12.924
8.610
6.869
5.959
5.408
5.041
4.781
4.587
4.437
4.31 8
4.221
4.140
4.073
4.015
3.965
3.922
3.883
3.850
3.81 9
3.792
3.768
3.745
3.725
3.707
3.690
3.674
3.659
3.646
3.551
3.496
3.460
3.435
3.41 6
3.402
3.390
3.357
3.340
3.2905

Applied Statistics
97
Probability Distributions for Discrete Random Variables
The
binomial distribution
applies to random variables where there are only two
possible outcomes
(A
or
B)
for each trial and where the outcome probability is
constant over all n trials. If the probability of
A
occurring on any one trial is
denoted as p and the number of occurrences of A is denoted as x, then the
binomial coefficient
is given by
and the probability of getting x occurrences of A in n trials is
The cumulative probability of the binomial distribution is given by
For the binomial distribution
P
=
"P
For np
2
5
and n( 1
-
p)
2
5,
an
approximation of binomial probabilities is given
by the standard normal distribution where
z
is a standard normal deviate and
The
negatiue binomial distribution
defines the probability of the
k'h
occurrence
of an outcome occurring on the xth trial as
and
(text
continued
on
page
102)
Table
1-20
Critical Values for the Chi-square Distrlbution
Degrees
of
Freedom
V
a
.9~ .995 .99O .975 .9SO
.9OO
.7W
SO0
.2O0
.lo0
.050
.020
.010 .005 .OO1
1.
.ooo
2. .002
3.
,024
4. .090
5. .209
6. ,377
7. ,597
8.
,850
9. 1.135
10. 1.446
11. 1.819
12. 2.188
13. 2.577
14. 3.018
15. 3.449
16. 3.894
,000
.010
,071
,205
,411
,673
,986
1.341
1.726
2.152
2.597
3.064
3.560
4.066
4.588
5.135
.ooo
,020
,115
,297
.553
,871
1.237
1.642
2.086
2.555
3.047
3.568
4.102
4.653
5.226
5.807
,001
.051
,216
,484
,831
1.236
1.688
2.179
2.699
3.244
3.815
4.402
5.006
5.624
6.260
6.905
,004
,102
,352
,711
1.145
1.635
2.167
2.732
3.324
3.938
4.574
5.225
5.890
6.568
7.260
7.960
,016
,211
,584
1.064
1.610
2.204
2.833
3.489
4.168
4.664
5.576
6.303
7.041
7.769
8.546
9.311
.146
,713
1.424
2,195
3.000
3.628
4.671
5.527
6.393
7.266
6.146
9.034
9.926
10.821
11.721
12.624
,455
1.386
2.366
3.357
4.352
5.349
6.346
7.344
8.343
9.342
10.341
11.340
12.340
13.339
14.339
15.339
1.642
3.219
4.642
5.989
7.291
6.559
9.804
11.031
12.243
13.443
14.633
15.813
16.986
16.152
19.312
20.466
2.706
4.604
6.252
7.782
9.237
10.646
12.020
13.363
14.686
15.990
17.278
18.551
19.614
21.067
22.310
23.546
3.842
5.995
7.817
9.492
11.073
12.596
14.070
15.512
16.925
18.311
19.681
21.030
22.367
23.691
25.000
26.301
5.405
7.822
9.841
11.660
13.385
15.033
16.624
18.171
19.663
21.165
22.623
24.059
25.477
26.879
28.266
29.640
6.637
9.221
11.325
13.280
15.088
16.610
16.471
20.082
21.654
23.194
24.755
26.246
27.717
29.169
30.605
32.027
7.905
10.569
12.819
14.624
16.762
18.550
20.270
21.936
23.563
25.154
26.714
28.249
29.878
31.376
32.857
34.321
10.809
13.691
16.292
16.432
20.751
22.677
24.527
26.318
28.061
29.763
31.431
33.070
34.683
36.272
37.842
39.392

17. 4.350
18. 4.864
19. 5.351
20. 5.848
21. 6.398
22. 6.919
23. 7.447
24. 8.027
25. 8.576
26. 9.130
27. 9.735
28. 10.306
29. 10.882
30. 11.509
40. 17.846
50. 24.609
60. 31.678
70. 38.980
80. 46.466
90. 54.104
100. 61.869
150. 102.073
5 687
6
251
6
825
7 422
8 018
8 622
9 247
9 869
10 498
I1
132
11
789
12 438
13092
13 767
20 669
27 957
35 503
43 246
51 145
59 171
67 303
109 122
6.400
7.004
7.627
8
252
8.886
9.528
10.187
10.846
11.510
12.190
12.868
13.551
14.240
14.943
22.139
29.685
37.465
45.423
53.523
61.738
70.049
112.655
7.560
8.225
8.904
9.587
10.278
10 976
11.685
12.397
13.115
13.837
14.565
15.304
16.042
16.784
24.423
32.349
40.474
48.750
57.147
65.641
74.218
117.980
8.670
9.388
10.114
10.849
11.590
12.336
13.088
13.845
14.607
15.377
16.149
16.925
17.705
18.488
26.508
34.763
43.187
51.739
60.391
69.126
77.929
122.692
200. 143.807 152.224 156.421 162.724 168.279
10.063
10.864
11
650
12.442
13.238
14.040
14.646
15.657
16.471
17.291
18.113
18.938
19.766
20.598
29.055
37.693
46.463
55.333
64.282
73.295
82.362
128.278
174.838
13.530
14.440
15.351
16.265
17.182
18.100
19.020
19.943
20.866
21.792
22.718
23.646
24.576
25.507
34.879
44.319
53.814
63.351
72.920
82.515
92.133
140.460
16.338
17.337
18.338
19.337
20.337
21.337
22.337
23.337
24.337
25.337
26.336
27.336
28.336
29.336
39.337
49.336
59.336
69.335
79.335
89.335
99.335
149.334
21.616
22.761
23.902
25.039
26.173
27.304
26.431
29.556
30.678
31.796
32.913
34.028
35.140
36.251
47.261
58.157
68.966
79.709
90.400
101.048
111.662
164.345
189.051 199.334 216.605
24.771
25.992
27.206
28.415
29.619
30.817
32.012
33. I99
34.384
35.566
36.745
37.920
39.092
40.261
51.796
63.159
74.390
85.521
96.572
107.559
118.493
172.577
226.017
27.593
28.877
30.148
31.416
32.678
33.933
35.178
36.421
37.660
38.894
40.119
41.344
42.565
43.762
55.753
67.501
79.078
90.528
101.876
11
3.143
124.340
179.579
31.002
32.353
33.694
35.026
36.350
37.666
38.975
40.277
41.573
42.863
44.147
45.426
46.699
47.968
60.443
72.619
84.586
96.393
108.075
119.654
131.147
187.683
33.435
34.831
36.216
37.591
38.957
40.314
41.862
43.004
44.338
45.665
46.986
48.301
49.610
50.914
63.710
76.172
88.396
100.441
112.344
124.1 30
135.820
193.219
35.771
37.208
38.633
40.046
41.449
42.843
44.228
45.604
46.973
48.334
49.688
51.036
52.378
53.713
66.802
79.523
91.982
104.243
116.348
128.324
140.1 93
198.380
40.926
42.444
43.949
45.440
46.919
48.387
49.845
51.293
52.732
54.162
55.584
56.998
58.405
59.805
73.490
86.740
99.679
112.383
124.901
137.267
149.505
209.310
233.993 243.191 249.455 255.281 267.579
Table
1-21
Critical Values
for
the Cumulative
F
Distrlbution
Degrees
of
Freedom
",
"*
1
2
345
6
7
8
9
10 15
20
30
40
50 100 500
lo00
loo00
1.
2.
3.
4.
5.
6.
7.
8.
161.
4052.
18.51
98.50
10.13
34.12
7.71
21.20
6.61
16.26
5.99
13.75
5.59
12.25
5.32
11.26
200.
5000.
19.00
99.00
9.55
30.82
6.94
18.00
5.79
13.27
5.14
10.92
4.74
9.55
4.46
8.65
216.
5403.
19.16
99.17
9.28
29.46
6.59
16.69
5.41
12.06
4.76
9.78
4.35
8.45
4.07
7.59
225.
5625.
19.25
99.25
9.12
28.71
6.39
15.98
5.19
11.39
4.53
9.15
4.12
7.85
3.84
7.01
230.
5764.
19.30
99.30
9.01
28.24
6.26
15.52
5.05
10.97
4.39
8.75
3.97
7.46
3.69
6.63
234.
5859.
19.33
99.33
8.94
27.91
6.16
15.21
4.95
10.67
4.28
8.47
3.87
7.19
3.58
6.37
237.
5928.
19.35
99.36
6.69
27.67
6.09
14.98
4.88
10.46
4.21
8.26
3.79
6.99
3.50
6.18
239.
5961.
19.37
99.37
8.85
27.49
6.04
14.80
4.82
10.29
4.15
8.10
3.73
6.84
3.44
6.03
241.
6022.
19.38
99.39
8.81
27.34
6.00
14.66
4.77
10.16
4.10
7.98
3.68
6.72
3.39
5.91
242.
6056.
19.40
99.40
8.79
27.23
5.96
14.55
4.74
10.05
4.06
7.87
3.64
6.62
3.35
5.81
246.
6157.
19.43
99.43
8.70
26.87
5.86
14.20
4.62
9.72
3.94
7.56
3.51
6.31
3.22
5.52
248.
6209.
19.45
99.45
8.66
26.69
5.80
14.02
4.56
9.55
3.87
7.40
3.44
6.16
3.15
5.36
250.
6261.
19.46
99.47
8.62
26.50
5.75
13.84
4.50
9.38
3.81
7.23
3.38
5.99
3.08
5.20
251.
6287.
19.47
99.47
8.59
26.41
5.72
13.75
4.46
9.29
3.77
7.14
3.34
5.91
3.04
5.12
252.
6303.
19.48
99.48
8.58
26.35
5.70
13.69
4.44
9.24
3.75
7.09
3.32
5.86
3.02
5.07
253.
6334.
19.49
99.49
8.55
26.24
5.66
13.58
4.41
9.13
3.71
6.99
3.27
5.75
2.97
4.96
254.
6360.
19.49
99.50
8.53
26.15
5.64
13.49
4.37
9.04
3.68
6.90
3.24
5.67
2.94
4.88
254.
6363.
19.49
99.50
8.53
26.14
5.63
13.47
4.37
9.03
3.67
6.89
3.23
5.66
2.93
4.87
254.
8364.
19.49
99.49
8.52
26.12
5.63
13.46
4.37
9.02
3.67
6.88
3.23
5.65
2.93
4.86
9
10.
15.
20.
30.
40.
50.
100.
500.
1000.
10000.
5.12
10.56
4.96
10.04
4.54
8.68
4.35
8.10
4.17
7.56
4.08
7.31
4.03
7.17
3.94
6.90
3.86
6.69
3.85
6.66
3.84
6.64
4.26
8.02
4.10
7.56
3.68
6.36
3.49
5.85
3 32
5.39
3.23
5.18
3.18
5.06
3.09
4.82
3.01
4.65
3.00
4.63
3.00
4.61
3.86
6.99
3.71
6.55
3.29
5.42
3.10
4.94
2.92
4.51
2.84
4.31
2.79
4.20
2.70
3.98
2.62
3.82
2.61
3.80
2.61
3.78
3.63
6.42
3.48
5.99
3.06
4.89
2.87
4.43
2.69
4.02
2.61
3.83
2.56
3.72
2.46
3.51
2.39
3.36
2.38
3.34
2.37
3.32
3.48
6.06
3.33
5.64
2.90
4.56
2.71
4.10
2.53
3.70
2.45
3.51
2.40
3.41
2.31
3.21
2.23
3.05
2.22
3.04
2.21
3.02
3.37
5.80
3.22
5.39
2.79
4.32
2.60
3.87
2.42
3.47
2.34
3.29
2.29
3.19
2.19
2.99
2.12
2.84
2.11
2.82
2.10
2.80
3.29
5 61
3 14
5.20
2.71
4.14
2.51
3.70
2.33
3.30
2.25
3.12
2.20
3.02
2.10
2.82
2.03
2.68
2.02
2.66
2.01
2.64
3.23
5.47
3.07
5.06
2.64
4.00
2.45
3.56
2.27
3.17
2.18
2.99
2.13
2.89
2.03
2.69
1.96
2.55
1.95
2.53
1.94
2.51
3.18
5.35
3.02
4.94
2.59
3.89
2.39
3.46
2.21
3.07
2.12
2.89
2.07
2.78
1.97
2.59
1.90
2.44
1.89
2.43
1.88
2.41
3.14
5.26
2.98
4.85
2.54
3.80
2.35
3.37
2.16
2.98
2.08
2.80
2.03
2.70
1.93
2.50
1.85
2.36
1.84
2.34
1.83
2.32
3.01
4.96
2.85
4.56
2.40
3.52
2.20
3.09
2.01
2.70
1.92
2.52
1.87
2.42
1.77
2.22
1.69
2.07
1.68
2.06
1.67
2.04
2.94
4.81
2.77
4.41
2.33
3.37
2.12
2.94
1.93
2.55
1.84
2.37
1.78
2.27
1.68
2.07
1.59
1.92
1.58
1.90
1.57
1.88
2.86
4.65
2.70
4.25
2.25
3.21
2.04
2.78
1.84
2.39
1.74
2.20
1.69
2.10
1.57
1.89
1.48
1.74
1.47
1.72
1.46
1.70
2.83
4.57
2.66
4.17
2.20
3.13
1.99
2.69
1.79
2.30
1.69
2.11
1.63
2.01
1.52
1.80
1.42
1.63
1.41
1.61
1.40
1.59
2.80
4.52
2.64
4.12
2.18
3.08
1.97
2.64
1.76
2.25
1.66
2.06
1.60
1.95
1.48
1.74
1.38
1.57
1.36
1.54
1.35
1.53
2.76
4.41
2.59
4.01
2.12
2.98
1.91
2.54
1.70
2.13
1.59
1.94
1.52
1.82
1.39
1.60
1.28
1.41
1.26
1.38
1.25
1.36
2.72
4.33
2.55
3.93
2.08
2.89
1.86
2.44
1.64
2.03
1.53
1.83
1.46
1.71
1.31
1.47
1.16
1.23
1.13
1.19
1.11
1.16
2.71
4.32
2.54
3.92
2.07
2.88
1.85
2.43
1.63
2.02
1.52
1.82
1.45
1.70
1.30
1.45
1.14
1.20
1.11
1.16
1.08
1.11
2.71
4.31
2.54
3.91
2.07
2.87
1.85
2.42
1.62
2.01
1.51
1.82
1.44
1.68
1.28
1.43
1.12
1.17
1.08
1.12
1.03
1.05
Note: The upper and lower values in the table are
for
F,,
and
Fo,.
U
U
0

102
Mathematics
(text continued from page
97)
If the probabilities do not remain constant over the trials and
if
there are
k
(rather than two) possible outcomes of each trial, the
hypergeometric distribution
applies. For a sample of size
N
of a population of size T, where
t,
+
t,
+
.
. . +
t,
=
T,
n,
+
n2
+
.
.
.
+
nt
=
N
and
the probability is
The
Poisson distribution
can be used to determine probabilities for discrete
random variables where the random variable is the number of times that an
event occurs in a single trial (unit of time, space, etc.). The probability function
for a Poisson random variable is
where
p
=
mean of the probability function (and also the variance)
The cumulative probability function is
Univariate Analysis
For Multivariate Analysis, see McCuen, Reference
23,
or other statistical texts.
The first step in data analysis
is
the selection of the best fitting probability
function, often beginning with a
graphical analysis
of the frequency histogram.
Moment ratios and
moment-ratio diagrams
(with
0,
as abscissa and
p,
as ordinate)
are useful since probability functions of known distributions have characteristic
values of
p,
and
p,.
Frequency analyszs
is an alternative
to
moment-ratio analysis in selecting a
representative function. Probability paper (see Figure
1-59
for an example) is
available for each distribution, and the function is presented as a cumulative
probability function. If the data sample has the same distribution function as
the function used to scale the paper, the data will plot as a straight line.
The procedure is to fit the population frequency curve as a straight line using
the sample moments and parameters
of
the proposed probability function. The
data are then plotted by ordering the data from the largest event to the smallest
and using the rank
(i)
of the event to obtain a probability plotting position.
Two of the more common formulas are Weibull
pp,
=
i/(n
+
1)

Applied Statistics
103
Excedence
Probability
(%)
99.99 99.9 99.8 99 98 95 90 80
70
60
50
40
30
20
10
5
2
1
.5
.2
.1
.05
200001
II
I
I I
Ill1
I I I I
IIl/lII
.
P
“r:
12000
u
10000
I
6000
4000
2000
0.01
K
=
8620
ft3/sec
s
=
4128
ft3/sec
A-L
05
.1
Ill01
I/I
IIIIIII
II
II
II
.2 .5
1
2
5
10
20
30
40
50
60 70
80 90 95 98 99 99.899.9
99
Figure
1-59.
Probability paper for frequency analysis.
and Hazen
where n is the sample size. If the data do not show a reasonable fit to the
population curve, a different function should be investigated.
Estimation of model parameters is frequently accomplished by the
method
of
moments.
For example, for the uniform distribution, the mean is
and the variance is
o2
=
(p
-
a)’/12
=
Sz
Solving for
a
and
p
gives
a
=
X-SA
p=X+S&
Confidence Intervals
Confidence intervals provide a method
of
calculating the range
of
values that
contains the true value of an estimate. A general equation for a two-sided
confidence interval is

104
Mathematics
where
K,,,
=
estimated value
of
the
K
statistic
F
=
distribution factor
D
=
measure
of
dispersion
(For one-sided confidence intervals, the
*
is replaced by
+
or by
-.)
If
(3
is
known, the
confidence interval on the mean
is
1.
Two sided
(3
-
(3
-
x-z,,--pIx++,,-
&- &
2.
One sided, lower limit
(3
-
x
-
z,
-
<
p
I
CQ
&-
3.
One sided, upper limit
(3
-
--m
I
p
I
X
+z,
-
J;;
where
=
sample mean
=
Kes,
n
=
sample size
Z,,Z~,~
=
values of random variables, with standard normal distribution,
cutting off
(1
-
y)
and
(1
-
y/2)
respectively in the tail of the
distribution, and
a
=
1
-
y
(the level of significance)
=
F
o/&
=
measure
of
dispersion
If
(3
is unknown, the equations are
1.
Two sided
2.
One sided, lower limit
S
-
x-
t,
-
<
p
I
&-
3.
One sided, upper limit
S
-
--m
I
I
x+
t,
-
VL
