Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay
Подождите немного. Документ загружается.


108 C. Nataraj and K. Kappaganthu
M
n
q
n
00
C .D
n
˝
n
G
n
/q
n
0
C K
n
q
n
D F
n
; (10.4)
where
M
n
D
10
01
D
n
D
2 0
02
G
n
D
0 ˛
˛0
K
n
D
10
0
2
q
n
D ŒV = l
1
W=l
1
T
(10.5)
This nondimensional form has been derived using the substitutions D !
y
t;
˝
n
D
˝
!
y
, !
y
D
q
k
y
m
;!
z
D
q
k
z
m
;D
!
z
!
y
;D
c
2
p
km
;˛D
I
p
ml
2
1
. is the
orthotropic parameter.
The nondimensional force is given by [8]
F
n
D
.w
0
˝
n
v/
2
C .v
0
C ˝
n
w/
2
1=2
v
0
C ˝
n
w
w
0
˝
n
v
(10.6)
D 0:64T
1 C l
1
=l
2
m!
2
y
l
2
1
(10.7)
10.3 Analysis
In this chapter, the nonlinear behavior of the isotropic system is analyzed, i.e, with
is equal to one. The nondimensional form of the equation, (10.4) is used for the anal-
ysis. The only nonlinearity in the system is from the force exerted by the spline. The
coupling between the two differential equations in (10.4) is primarily due to the gy-
roscopic matrix. The system is studied for variation in response with changes in the
nondimensional spin speed, ˝
n
.
The system has fixed points at
v
1
D 0; w
1
D 0; (10.8)
v
2
D
p
1 C
2
; w
2
D
p
1 C
2
(10.9)

10 Nonlinear Response in a Rotor System With a Coulomb Spline 109
v
3
D
p
1 C
2
; w
3
D
p
1 C
2
(10.10)
No fixed points are created or destroyed with changes in ˝
n
; further, the eigen-
values of the system linearized about each of the fixed points suggest that each of
these points is unstable for all values of ˝
n
.
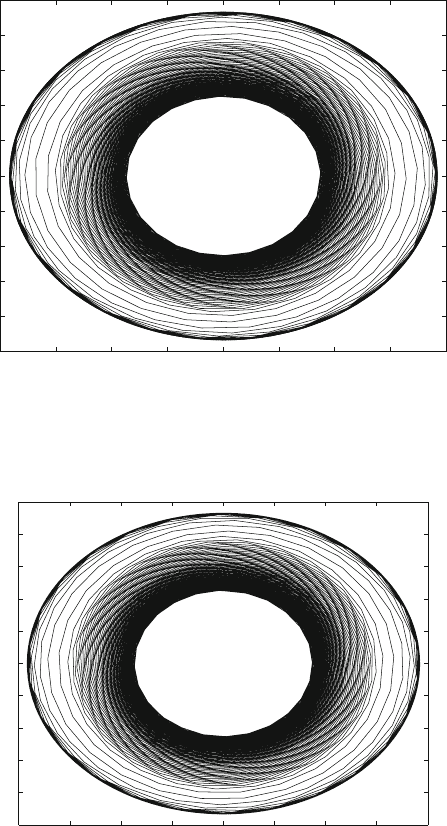
Owing to the isotropy, the limit cycle, if it exists, must be a circular orbit in y–z
plane. For such a solution, v D A
o
cos !
n
and w D A
o
sin !
n
. Substituting these
into (10.4) and solving
˝
n
<!
n
No limit cycle exists
˝
n
>!
n
Limit cycle exists; with (10.11)
!
n
D
˝
n
˛
2
C
s
1 C
˝
n
˛
2
2
(10.12)
A
o
D
2!
n
: (10.13)
The critical value of the spin speed from (10.11), (10.12)isgivenby
˝
n; critical
D
1
p
1 ˛
(10.14)
The limit cycle and the transients obtained at ˝
n
D 1:3 are shown in
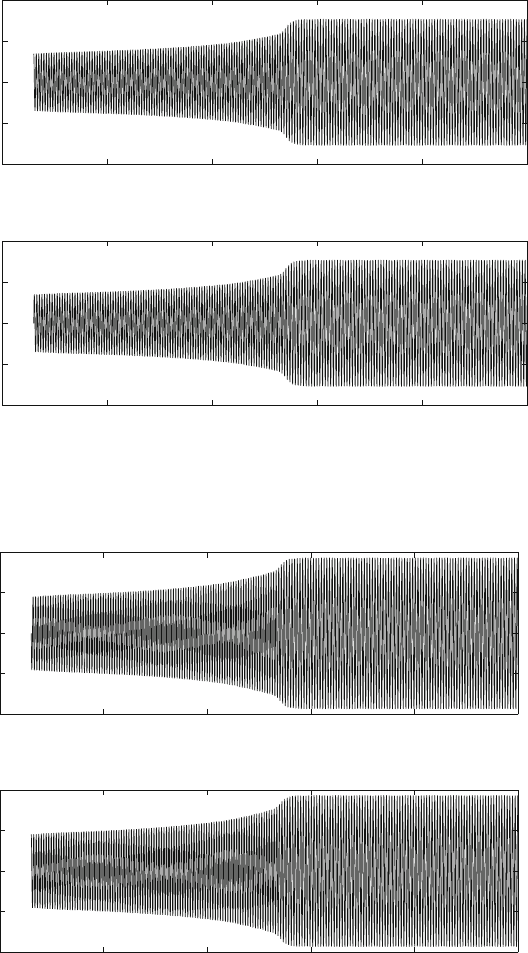
Figs. 10.3–10.7. The parameters used for the simulation are given in Table 10.1.
For these chosen values, ˝
n; critical
D 1:1952. The bifurcation diagram is shown in
Fig. 10.8.
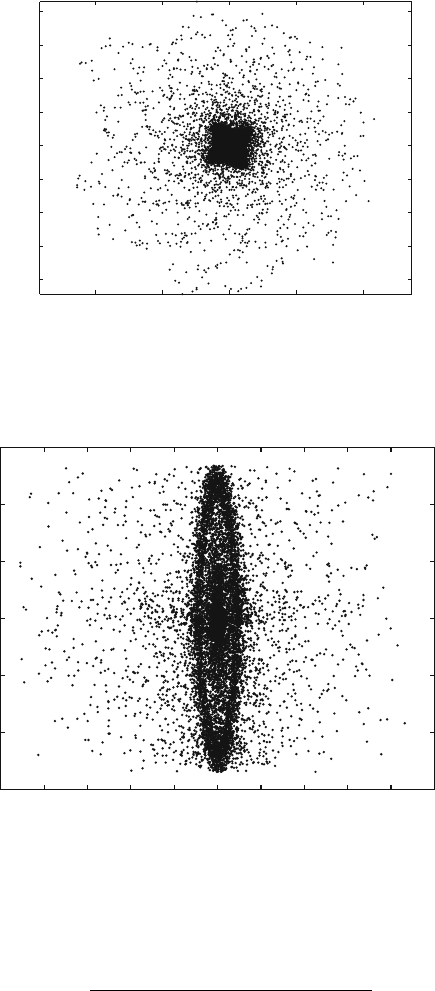
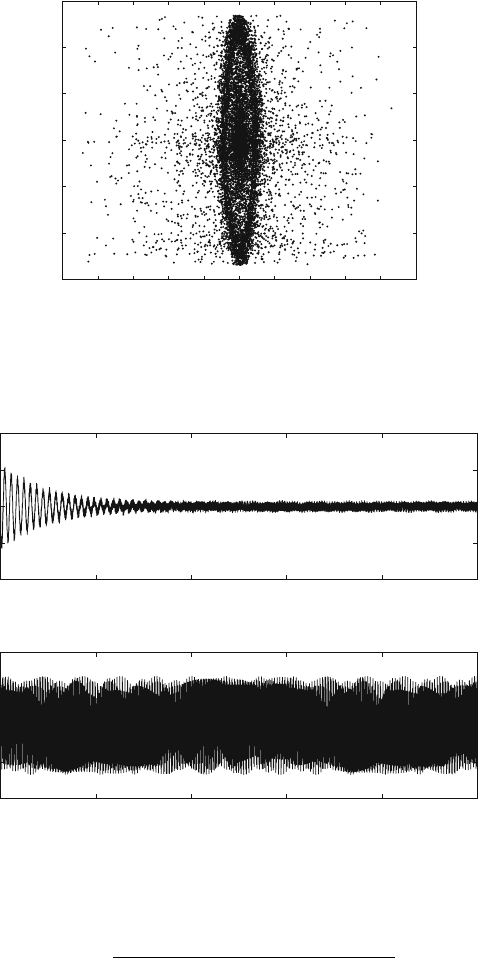
It has also been observed that, but for certain initial conditions close to the
limit cycle, the system settles into a stable limit cycle only after very large chaotic
transients. These transients are shown in Figs. 10.9–10.13. The presence of such
transient chaos suggests the presence of strange attractors and crisis. The presence
of crisis as a possible route of chaos is explained in [2]and[3].
The phenomenon of crisis occurs when there is a “collision between a chaotic
attractor and a coexisting unstable fixed point or periodic orbit” [2]. In this system,
the crisis occurs because of the presence of an unstable fixed points at
v
2
w
2
and
v
3
w
3
. Numerical simulations about
v
1
w
1
show that it is a strange attractor.
Different ODE solvers in MATLAB give similar results.
The system response at subcritical speeds is shown in Figs. 10.14–10.17.
A zoomed in view of the response in v and w isshowninFigs.10.18 and 10.19
respectively. The response seems to divide itself, however it is difficult to establish
the presence of fractals in the four dimensional space.
In order to rule out the possibility of a quasi periodic orbit, the volume of the
state space is analyzed. Proceeding as in [9], the state space form of (10.4)is
P
x D f.x/; (10.15)
110 C. Nataraj and K. Kappaganthu
−0.05 0 0.05 0.1
v
w
−0.06
−0.04
−0.02
0
0.02
0.04
0.06
0.08
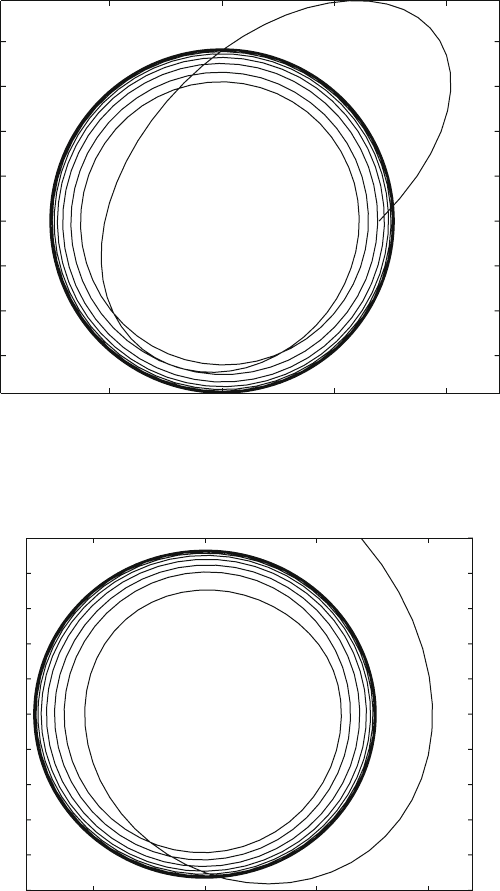
Fig. 10.3 Orbit in a limit cycle
−0.05 0 0.05 0.1
v
vdot
−0.1
−0.08
−0.06
−0.04
−0.02
0
0.02
0.04
0.06
0.08
0.1
Fig. 10.4 Phase plane v vs. Pv
10 Nonlinear Response in a Rotor System With a Coulomb Spline 111
−0.08 −0.06 −0.04 −0.02 0 0.02 0.04 0.06 0.08 0.1
−0.1
−0.05
0
0.05
0.1
0.15
w
wdot
Fig. 10.5 Phase plane w vs. Pw
0 50 100 150 200 250
−0.1
0
0.1
0.2
0.3
τ
v
0 50 100 150 200 250
−0.1
−0.05
0
0.05
0.1
τ
w
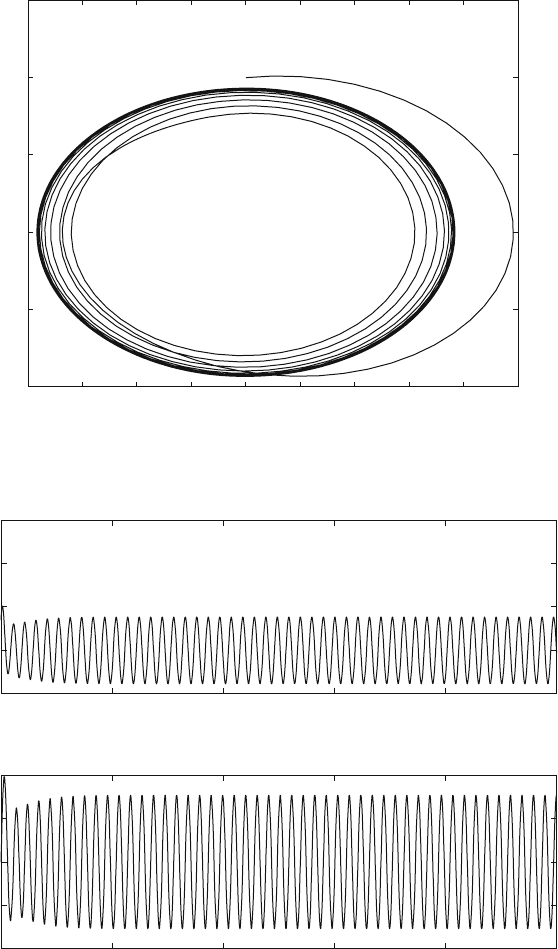
Fig. 10.6 Variation of v and w
112 C. Nataraj and K. Kappaganthu
0 50 100 150 200 250
τ
vdot
0 50 100 150 200 250
τ
wdot
−0.1
−0.05
0
0.05
0.1
−0.1
0
0.1
0.2
0.3
Fig. 10.7 Variation of Pv and Pw
Table 10.1 Parameter values
Parameter Value
˛ 0.3
0.1
0.01867
1
where
x D
h
vwv
0
w
0
i
T
(10.16)
f D
2
6
6
6
6
6
6
6
6
6
6
6
6
4
v
0
w
0
2v
0
˝
n
˛w
0
v
v
0
C ˝
n
w
h
w
0
˝
n
v
2
C
v
0
C ˝
n
w
2
i
1=2
2w
0
˝
n
˛v
0
2
w
w
0
˝
n
v
h
w
0
˝
n
v
2
C
v
0
C ˝
n
w
2
i
1=2
3
7
7
7
7
7
7
7
7
7
7
7
7
5
:
(10.17)
Using divergence theorem, the volume rate of the state space is given by
V
0
D
Z
gradf dV: (10.18)
10 Nonlinear Response in a Rotor System With a Coulomb Spline 113
0 0.5 1 1.5 2 2.5
0.04
0.045
0.05
0.055
0.06
0.065
0.07
0.075
0.08
Ω
n
Amplitude
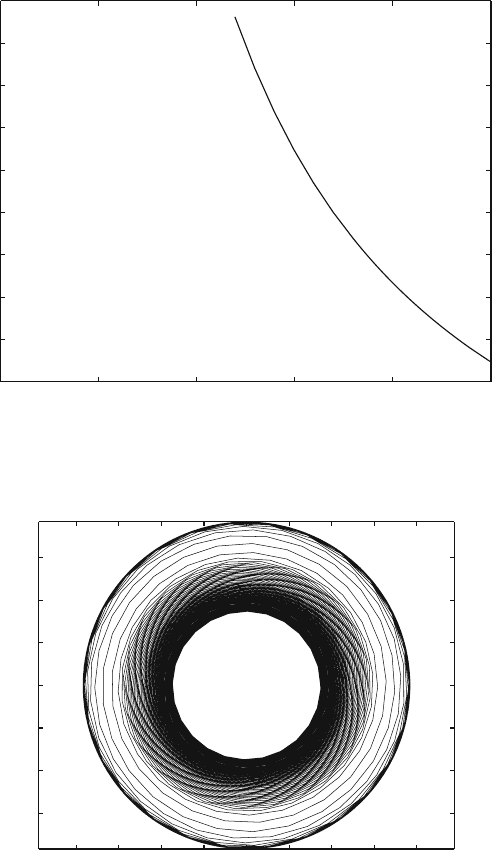
Fig. 10.8 Bifurcation diagram
−0.08 −0.06 −0.04 −0.02 0 0.02 0.04 0.06 0.08
−0.06
−0.04
−0.02
0
0.02
0.04
0.06
v
w
Fig. 10.9 Transient chaos followed by a limit cycle
For the system to exhibit a chaotic motion, the volume in the state space should
shrink exponentially fast [9], and there should be no stable fixed points or limit
cycles. The second part of the condition has already been shown. To look at the
volumes, the system is linearized about
v
1
w
1
. The linearization matrix of the
system is as shown in (10.19).
114 C. Nataraj and K. Kappaganthu
−0.08 −0.06 −0.04 −0.02 0 0.02 0.04 0.06 0.08
−0.1
−0.08
−0.06
−0.04
−0.02
0
0.02
0.04
0.06
0.08
0.1
v
vdot
Fig. 10.10 Phase plane in transient chaos (v vs. Pv/
−0.08 −0.06 −0.04 −0.02 0 0.02 0.04 0.06 0.08
w
wdot
−0.1
−0.08
−0.06
−0.04
−0.02
0
0.02
0.04
0.06
0.08
0.1
Fig. 10.11 Phase plane in transient chaos (w vs. Pw/
A D
2
6
6
4
00 1 0
00 0 1
1 C L
1
L
2
2 C L
3
˝
n
˛ C L
4
L
5
2
C L
6
˝
n
˛ C L
7
2 C L
8
3
7
7
5
; (10.19)
10 Nonlinear Response in a Rotor System With a Coulomb Spline 115
0 200 400 600 800 1000
τ
v
0 200 400 600 800 1000
−
τ
w
−0.1
−0.05
0
0.05
0.1
−0.1
0.05
0
0.05
0.1
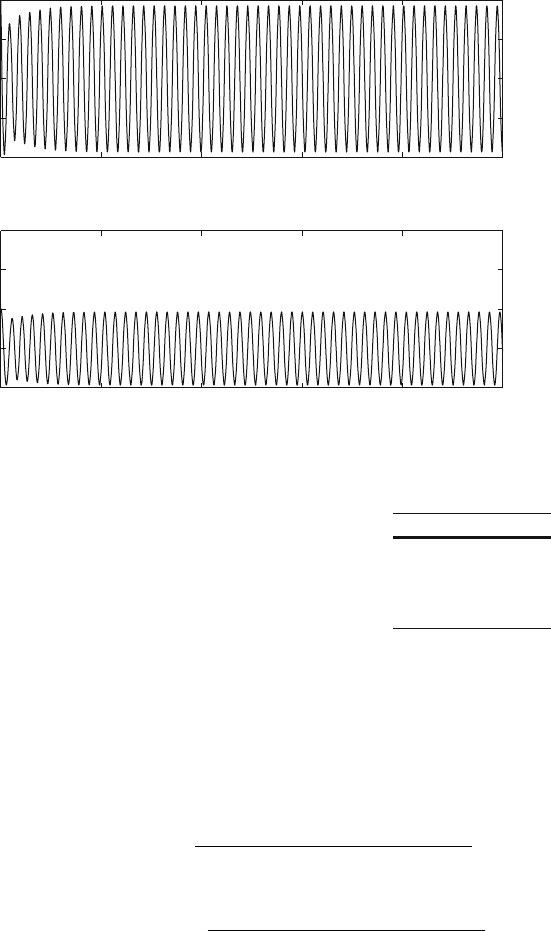
Fig. 10.12 Variation of v and w in transient chaos
0 200 400 600 800 1000
−0.1
−0.05
0
0.05
0.1
τ
vdot
0 200 400 600 800 1000
−
0
−0.1
0.05
0.05
0.1
τ
wdot
Fig. 10.13 Variation of Pv and Pw in transient chaos
116 C. Nataraj and K. Kappaganthu
−2 −1 0 1 2
x 10
−7
x 10
−7
v
w
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
Fig. 10.14 Chaotic response
−2.5 −2 −1.5 −1 −0.5 0 0.5 1 1.5 2 2.5
x 10
−7
−3
−2
−1
0
1
2
3
x 10
−5
v
vdot
Fig. 10.15 Phase plane view of chaos (v vs. Pv/
where
L
1
D
˝
n
.w
d
˝
n
v/.v
d
C ˝
n
w/
.w
d
˝
n
v/
2
C .v
d
C ˝
n
w/
2
3=2
; (10.20)
10 Nonlinear Response in a Rotor System With a Coulomb Spline 117
−2 −1.5 −1 −0.5 0 0.5 1 1.5 2 2.5
x 10
−7
x 10
−5
w
wdot
−2.5
−3
−2
−1
0
1
2
3
Fig. 10.16 Phase plane view of chaos (w vs. Pw/
0 100 200 300 400 500
−4
−2
0
2
4
x 10
−7
τ
0 100 200 300 400 500
−4
−2
0
2
4
x 10
−5
τ
vvdot
Fig. 10.17 Variation of v and Pv in chaos
L
2
D
˝
n
.w
d
˝
n
v/
2
.w
d
˝
n
v/
2
C .v
d
C ˝
n
w/
2
3=2
; (10.21)
