Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay
Подождите немного. Документ загружается.

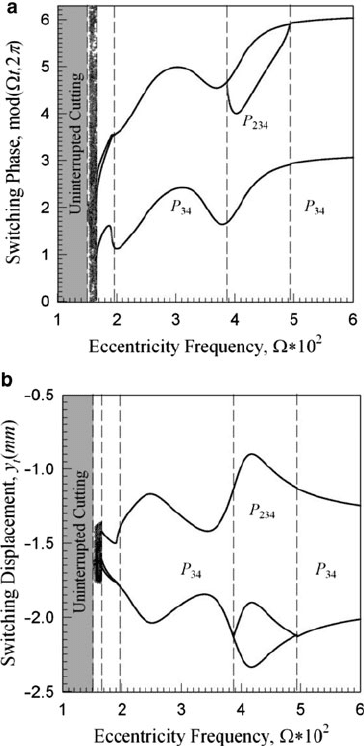
88 B.C. Gegg et al.
The P
34
steady state motion dominates the largest frequency span, but is interrupted
by the P
234
steady state motion; see Figs. 8.8 and 8.9. As noted in Gegg [12], the
route to an unstable state caused by the transient/steady state interference with chip
seizure motion is observed with decreasing eccentricity frequency . The switching
phase components are noted to nearly fill the spectrum, implying that the motion
may be chaotic. Verification of the introduction of chip seizure motion is noted in
Fig. 8.9a, b by the switching forces and force products. Table 8.1 summarizes the
motions and changes in the steady state structure throughout the frequency range.
Fig. 8.8 Numerical and
analytical predictions of
(a) switching phase
mod.t
i
;2/,(b) switching
displacement Qy for
interrupted periodic motions
over a range of eccentricity
frequency for
e D 0:275 mm and
L
c
D 1:0 mm
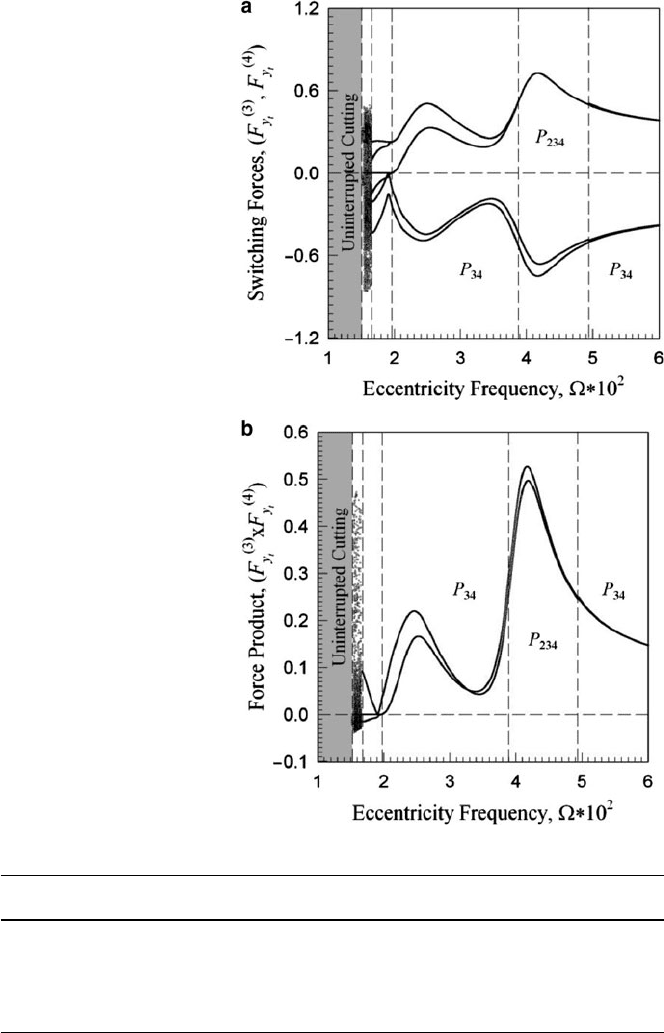
8 A Parameter Study of a Machine Tool with Multiple Boundaries 89
Fig. 8.9 Numerical and
analytical predictions of
(a) switching forces
F
.3/
Qy
and F
.4/
Qy
,and
(b) switching force product
F
.3/
Qy
F
.4/
Qy
for interrupted
periodic motions over a range
of eccentricity frequency
for e D 0:275 mm and,
L
c
D 1:0 mm
Table 8.1 Summary of eccentricity frequencies for specific motions for e D 0:275; L
c
D 1:0
Mapping
structure
Eccentricity
frequency
Grazing bifurcation
of boundary
Chip seizure
bifurcation
P
.034/
n
.0:1520k; 1656k .rad=s/D
3
W 0:1520k
P
034
.0:1656k; 0:1970k .rad=s/D
3
W 0:1656k .rad=s/ 0:1656k .rad=s/
P
34
.0:1970k; 0:3869k .rad=s/D
3
W 0:1970k .rad=s/ 0:1970k .rad=s/
P
234
.0:3869k; 0:4923k .rad=s/D
4
W 0:3869k .rad=s/
P
34
.0:4923k; 0:6k .rad=s/D
4
W 0:4923k .rad=s/ 0:1970k .rad=s/

90 B.C. Gegg et al.
8.7 Summary and Conclusions
The steady state motion for a machine-tool has been studied over the three
parameters: eccentricity frequency and amplitude, and chip length. The prelim-
inary discussion of notable phenomena is developed through sketches and their
governing equations. The steady state chip seizure with a near grazing motion is
developed and observed in ensuing simulations. The parameters maps expressing
the MFP, the NOM, and the MAG were presented alone and in two combinations.
One combination shows the MFP and the NOM overlay; where the motions and
complexity can be clearly defined. The second combination shows the MAG with
the NOM overlaid to express the size of the orbit and extent the motion interacts
with the chip/tool friction boundary. These parameter maps were completed for two
chip lengths, where the motion structure could be observed for effects on the size
and location of unstable/chaotic regions. The numerical prediction of two parameter
ranges of the eccentricity frequency is completed; one for each chip length. Such
is completed to explain the onset of the complex motion noted in Figs. 8.8 and
8.9. This study claims that the measure developed herein by observing not only
a single quantity of the motion structure (which has been traditionally accepted
protocol), but all the switching component in the motion structure and summariz-
ing the motion with several output measures such as the NOM, the MFP and the
MAG. are necessary and sufficient to characterize this machine-tool system and any
interconnected dynamics of continuous systems.
Appendix
The dynamical system damping parameters for this machine-tool system with free
vibration of the tool-piece motion, domain †
i
,fori D 1,are
fD
.i/
gD
2
4
d
.i/
11
d
.i/
12
d
.i/
21
d
.i/
22
3
5
; (8.34)
where
d
.i/
11
D
1
m
d
x
;d
.i/
12
D d
.i/
21
D 0; d
.i/
22
D
1
m
d
y
: (8.35)
The stiffness parameters in domain †
i
for i D 1,are
fK
.i/
gD
2
4
k
.i/
11
k
.i/
12
k
.i/
21
k
.i/
22
3
5
; (8.36)
8 A Parameter Study of a Machine Tool with Multiple Boundaries 91
where
k
.i/
11
D
1
m
2
k
x
;k
.i/
12
D k
.i/
21
D 0; k
.i/
22
D
1
m
2
k
y
: (8.37)
The external force parameters in domain †
i
,fori D 1,are
a
.i/
D
h
a
.i/
x
a
.i/
y
i
T
; b
.i/
D
h
b
.i/
x
b
.i/
y
i
T
; c
.i/
D
h
c
.i/
x
c
.i/
y
i
T
; (8.38)
where
a
.i/
x
D a
.i/
y
D b
.i/
x
D b
.i/
y
D c
.i/
x
D c
.i/
y
D 0; (8.39)
respectively. The dynamical system damping parameters for this machine-tool sys-
tem undergoing tool and work-piece in contact but no cutting, in domain †
i
,for
i D 2,are
d
.i/
11
D
1
m
Œd
x
C d
1
sin
2
ˇ;
d
.i/
12
D
1
m
Œd
1
cos ˇ sin ˇ;
d
.i/
21
D
1
m
Œd
1
sin ˇ cos ˇ;
d
.i/
22
D
1
m
Œd
y
C d
1
cos
2
ˇ:
9
>
>
>
>
>
>
>
>
>
>
=
>
>
>
>
>
>
>
>
>
>
;
(8.40)
The stiffness parameters in domain †
i
,fori =2,are
k
.i/
11
D
1
m
2
Œk
x
C k
1
sin
2
ˇ;
k
.i/
12
D
1
m
2
Œk
1
cos ˇ sin ˇ;
k
.i/
21
D
1
m
2
Œk
1
cos ˇ sin ˇ;
k
.i/
22
D
1
m
2
Œk
y
C k
1
cos
2
ˇ:
9
>
>
>
>
>
>
>
>
>
>
=
>
>
>
>
>
>
>
>
>
>
;
(8.41)
The external force parameters in domain †
i
,fori D 2 are
a
.i/
x
D e
m
e
m
sin ; a
.i/
y
D e
m
e
m
cos ; b
.i/
x
D b
.i/
y
D 0 (8.42)
and
c
.i/
x
D
1
m
2
fk
1
Œx
1
sin ˇ y
1
cos ˇsin ˇ;
c
.i/
y
D
1
m
2
fk
1
Œx
1
sin ˇ y
1
cos ˇcos ˇ;
9
>
=
>
;
(8.43)
92 B.C. Gegg et al.
respectively. The dynamical system damping parameters for this machine-tool
system undergoing tool and work-piece in contact but with cutting, in domain †
i
,
for i D 3,4,are
d
.i/
11
D
1
m
Œd
x
C d
1
sin
2
ˇ C d
2
cos ˛.cos ˛ .1/
i
sin ˛/;
d
.i/
12
D
1
m
Œd
1
cos ˇ sin ˇ d
2
sin ˛.cos ˛ .1/
i
sin ˛/;
9
>
=
>
;
(8.44)
and
d
.i/
21
D
1
m
Œd
1
sin ˇ cos ˇ d
2
cos ˛.sin ˛ C .1/
i
cos ˛/;
d
.i/
22
D
1
m
Œd
y
C d
1
cos
2
ˇ C d
2
sin ˛.sin ˛ C .1/
i
cos ˛/:
9
>
=
>
;
(8.45)
The stiffness parameters in domain †
i
,fori D 3,4,are
k
.i/
11
D
1
m
2
Œk
x
C k
1
sin
2
ˇ C k
2
cos ˛.cos ˛ .1/
.i/
sin ˛/;
k
.i/
12
D
1
m
2
Œk
1
cos ˇ sin ˇ C k
2
sin ˛.cos ˛ .1/
.i/
sin ˛/;
9
>
=
>
;
(8.46)
and
k
.i/
21
D
1
m
2
Œk
1
cos ˇ sin ˇ k
2
cos ˛.sin ˛ C .1/
.i/
cos ˛/;
k
.i/
22
D
1
m
2
Œk
y
C k
1
cos
2
ˇ C k
2
sin ˛.sin ˛ C .1/
.i/
cos ˛/:
9
>
=
>
;
(8.47)
The external force parameters in domain †
i
,fori D 3,4,are
a
.i/
x
D e
m
e
m
sin ; a
.i/
y
D e
m
e
m
cos ; b
.i/
x
D b
.i/
y
D 0 (8.48)
and
c
.i/
x
D
1
m
2
˚
k
1
x
1
sin ˇ y
1
cos ˇ
sin ˇ
Ck
2
x
2
cos ˛ y
2
sin ˛
cos ˛ .1/
.i/
sin ˛
;
c
.i/
y
D
1
m
2
˚
k
1
x
1
sin ˇ y
1
cos ˇ
cos ˇ
Ck
2
x
2
cos ˛ C y
2
sin ˛
sin ˛ C .1/
.i/
cos ˛
;
9
>
>
>
>
>
>
=
>
>
>
>
>
>
;
(8.49)
respectively. The dynamical system damping parameters for this machine-tool
system undergoing tool and work-piece in contact but with cutting, in domain †
i
,
for i D 0,are

8 A Parameter Study of a Machine Tool with Multiple Boundaries 93
Q
d
.i/
11
D
1
2m
d
2
C d
1
sin
2
.˛ C ˇ/ C d
x
cos
2
˛ C d
y
sin
2
˛
; (8.50)
and
Q
d
.i/
12
D
Q
d
.i/
21
D
Q
d
.i/
22
D 0. The stiffness parameters in domain †
i
,fori D 0,are
Q
k
.i/
11
D
1
m
2
k
1
sin
2
.˛ C ˇ/ C k
2
C k
x
cos
2
˛ C k
y
sin
2
˛
; (8.51)
and
Q
k
.i/
12
D
Q
k
.i/
21
D
Q
k
.i/
22
D 0. The external force parameters in domain †
i
,for
i D 0,are
Qa
.i/
x
D e
m
e
m
sin. ˛/; Qa
.i/
y
D 0; (8.52)
Q
b
.i/
x
D
V
m
k
1
cos.˛ C ˇ/ sin.˛ C ˇ/ C .k
x
k
y
/ cos ˛ sin ˛
;
Q
b
.i/
y
D 0 (8.53)
and
Qc
.i/
x
D
1
m
2
fŒd
1
N
V k
1
.
N
Vt
0
CQy
0
/ cos.˛ C ˇ/
Ck
1
Œx
1
sin ˇ y
1
cos ˇgsin.˛ C ˇ/ C Œ
N
V.d
x
d
y
/
C.
N
Vt
0
ı
CQy
0
/.k
y
k
x
/ cos ˛ sin ˛ Ck
2
Qx
2
; (8.54)
respectively. The tilde noted parameters can be referred to in the .x; y/ coordinate
system by
ƒ
Q
a
.i/
D ƒ
h
Qa
.i/
x
Qa
.i/
y
i
T
D a
.i/
D
h
a
.i/
x
a
.i/
y
i
T
; (8.55)
ƒ
Q
b
.i/
D ƒ
h
Q
b
.i/
x
Q
b
.i/
y
i
T
D b
.i/
D
h
b
.i/
x
b
.i/
y
i
T
; (8.56)
and
ƒ
Q
c
.i/
D ƒ
h
Qc
.i/
x
Qc
.i/
y
i
T
D c
.i/
D
h
c
.i/
x
c
.i/
y
i
T
: (8.57)
References
1. Traverso MG, Zapata R, Schmitz TL, Abbas AE (2009) Optimal experimentation for selecting
stable milling parameters: a Bayesian approach. In: Proceedings of the ASME 2009 interna-
tional manufacturing science and engineering conference MSEC2009-84032
2. Chandrasekaran H, Thoors H (1994) Tribology in interrupted machining: role of interruption
cycle and work material. Wear 179:83–88
3. Wiercigroch M (1997) Chaotic vibration of a simple model of the machine tool-cutting process
system. Trans ASME J Vib Acoust 119:468–475
94 B.C. Gegg et al.
4. Navarro-Lopez EM (2009) An alternative characterization of bit-sticking phenomena in a
multi-degree-of-freedom controlled drillstring. Nonlinear Anal Real World Appl 10(5):3162–
3174
5. Luo AC (2005) A theory for non-smooth dynamical systems on connectable domains. Commun
Nonlinear Sci Numer Simul 10:1–55
6. Gegg BC, Suh CS, Luo ACJ (2008) Chip stick and slip periodic motions of a machine tool in
the cutting process. In: ASME manufacturing science and engineering conference proceedings,
MSEC ICMP2008/DYN-72052
7. Gegg BC, Suh CS, Luo ACJ (2008) Periodic motions of a machine tool with intermittent
cutting. In: International mechanical engineering conference and exposition proceedings,
IMECE ASME2008/VIB-67109
8. Gegg BC, Suh Steve, Luo ACJ (2008) Analytical prediction of interrupted cutting periodic
motions in a machine tool. NSC2008-97, NSC, Porto, Portugal
9. Luo AC, Gegg BC (2004) Grazing phenomena in a periodically forced, linear oscillator with
dry friction. Commun Nonlinear Sci Numer Simul 11(7):777–802
10. Gegg BC, Suh CS, Luo ACJ (2007) Periodic motions of the machine tools in cutting process.
DETC2007/VIB-35166, Las Vegas, Nevada
11. Gegg BC, Suh S, Luo ACJ (2009) Interrupted cutting periodic motions in a machine tool with
a friction boundary, Part I: modeling and theory. ASME J Manuf Sci Eng (in press 2010)
12. Gegg BC (2009) An investigation of the complex motions inherent to machining systems via
a discontinuous systems theory approach. PhD dissertation, Texas A&M University, College
Station, Texas

Chapter 9
A New Friction Model for Evaluating Energy
Dissipation in Carbon Nanotube-Based
Composites
Yaping Huang and X.W. Tangpong
Abstract Being lighter and stiffer than traditional metallic materials,
nanocomposites have great potential to be used as structural damping materials
for a variety of applications. Studies of friction damping in the nanocomposites are
largely experimental, and there has been a lack of understanding of the damping
mechanism in nanocomposites. A new friction model is developed to study the
energy dissipation at the interface between carbon nanotube (CNT) and polymer
matrix under dynamic loading. Iwan’s distributed friction model is considered in
order to capture the stick/slip phenomenon at the interface. The effects of several pa-
rameters on energy dissipation are investigated, including the excitation’s frequency
and amplitude, and the interaction between CNT’s ends and matrix. A compliance
number is introduced to evaluate the energy dissipation for different contact inter-
faces. Some of the results are compared well with experimental observations in the
literature.
9.1 Introduction
Friction damping refers to the conversion of kinetic energy associated with the
motion of vibrating surfaces to thermal energy through friction between them [1].
Adding friction damping into a dynamic system can be a useful and practical
means to control mechanical vibration passively, particularly in high temperature
applications. There are various methods to introduce additional damping into a
system, for example, through (1) the incorporation of a damper (such as a ring)
in automotive and turbomachinery applications [2–5], (2) piezoelectric materials
and shunted electrical circuits [6, 7], (3) electro-rheological/magneto-rheological
fluids [8, 9], and (4) viscoelastic and elastomeric materials [10, 11]. While
viscoelastic materials offer good damping performance, their thermal stability
becomes an issue in high temperature environments and many of their mechanical
X.W. Tangpong (
)
Department of Mechanical Engineering, North Dakota State University, Fargo, ND 58108, USA
e-mail: annie.tangpong@ndsu.edu
A.C.J. Luo (ed.), Dynamical Systems: Discontinuity, Stochasticity and Time-Delay,
DOI 10.1007/978-1-4419-5754-2
9,
c
Springer Science+Business Media, LLC 2010
95
96 Y. Huang and X.W. Tangpong
properties start to degrade as the temperature rises. Those conventional methods
also pose challenges when it comes to integration into heterogeneous systems due
to limitations on space, weight, thermal stability, and damper reliability [12]. One
solution is to engineer the desirable amount of damping directly into composite
materials to develop light-weight and durable structure damping composites that
can be easily integrated into various systems. With the rapid development of nan-
otechnology in the last decade, an attractive opportunity rises as to engineer such
high damping performance composite materials by adding nanoscale fillers such as
carbon nanotubes (CNTs) into polymer composites (see Refs. 12, 13 and the refer-
ences therein) for a variety of mechanical, civil, military, aerospace, and aeronautics
applications. Due to CNT’s thermal stability, the CNT-reinforced nanocomposites
can be used as structural damping materials for extreme temperature applications.
The properties of nanocomposite, including the damping capacity, are highly de-
pendent on the fabrication method and processing techniques used. The damping
properties of nanocomposites have been studied experimentally [12–20]. Dynamic
mechanical analysis (DMA) tests of nanocomposites with different weight fractions
of CNTs showed that the reinforcement of CNTs could have significant influence
to the material’s damping capacity, and both temperature and frequency affected
the damping [14, 15]. Through mechanical cyclic test, the damping property of
CNT-based composites has been found to be dependent on strain, temperature,
CNTs’ weight fraction, and dispersion [16–18]. Friction damping can also be de-
termined from frequency response of the material sample using an accelerometer
and spectrum analyzer. Usually, a film of nanocomposite material is put in between
piezoelectric, epoxy, or metal sheets to form a sandwich beam, and the vibration of
the beam’s tip is then measured under cantilevered boundary condition. A critical
weight fraction of the CNTs has been found to exist for maximum damping of the
composite [12, 19, 20]. From these experimental studies, it was hypothesized that
energy dissipation in nanocomposites was due to interfacial slippage between the
CNTs and the matrix.
In the limited modeling work on evaluating friction damping of nanocompos-
ites, the stick–slip phenomenon between the CNTs and the polymer matrix has been
well accepted [12, 13, 19–22]. Generally, CNT is modeled as a solid cylinder, and
interfacial slippage takes place along the CNT–matrix interface when the interfacial
shear stress reaches a critical value [19]. The molecular dynamics (MD) method was
used to calculate the energy dissipation due to intertube friction in [21], where the
boundary conditions of the nanotube cluster were considered to be periodic [21],
though CNTs do not have continuous geometry. Shear lag analysis was also well
accepted in modeling the interfacial slippage of CNT–matrix [13, 19]. Other mod-
eling methods include (sandwiched) beam vibration analysis [12, 20, 23] and finite
element analysis [19, 24]. These aforementioned models did not take into account
the spatially distributed nature of the CNTs and did not consider varying interfa-
cial stiffness across the CNT–matrix interface. A major property of the CNT is its
high aspect ratio (length is much larger than diameter). When friction contact is
across a spatially distributed interface, the interfacial stiffness is not constant across
the interface and, therefore, should be treated in a statistical sense. The spatially
9 A New Model for Evaluating Energy Dissipation 97
varying interfacial stiffness, coupled with nonuniform pressure distribution as a re-
sult of material processing, could activate partial stick–slip motion, which is critical
in determining energy dissipation. In this chapter, a friction model is developed
considering the spatially distributed nature of CNT–matrix contact. Based on the
developed model, dynamic analysis of energy dissipation at CNT–matrix interface
considering multiple properties of the CNTs are performed. The results agree with
some experimental results from the literature qualitatively.
9.2 Vibration Model
To describe the spatially distributed nature of CNT–matrix contact, the distributed-
element friction model of Iwan [25,26] is adopted in this work. This model is based
on the concept of a large number of ideal elasto-plastic elements having different,
and statistically distributed, yield levels. The model is capable of simulating hystere-
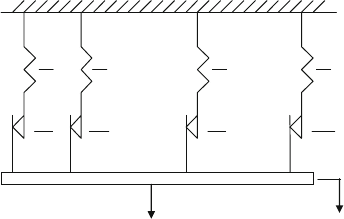
sis characteristics with nonlocal memory [27]. Figure 9.1 illustrates a parallel-series
distributed-element model of Jenkin’s (or Maxwell-slip) elements, and each consists
of a linear spring of stiffness K=N in series with a Coulomb damper of a slip force
f
i
=N ,whereN is the number of elements. The force–deflection relation of one
element is depicted in Fig. 9.2, and upon initial loading, the reaction force is
F D
n
X
iD1
f
i
=N C kx.N n/=N; (9.1)
where n is the number of elements that have slipped, while the remainder stick. In
the limit of very large N , the slip force is expressed in terms of the distribution
function ',and(9.1) is written in the equivalent form:
F D
Z
kx
0
f
'.f
/df
C kx
Z
1
kx
'.f
/df
; Px>0; (9.2)
Fig. 9.1 Distributed
hysteresis model
N
k
N
f
*
1
N
k
N
f
*
2
N
k
N
f
i
*
N
k
N
f
N
*
⋅⋅⋅ ⋅⋅⋅
F
x
