Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay
Подождите немного. Документ загружается.

58 J.-J. Lou et al.
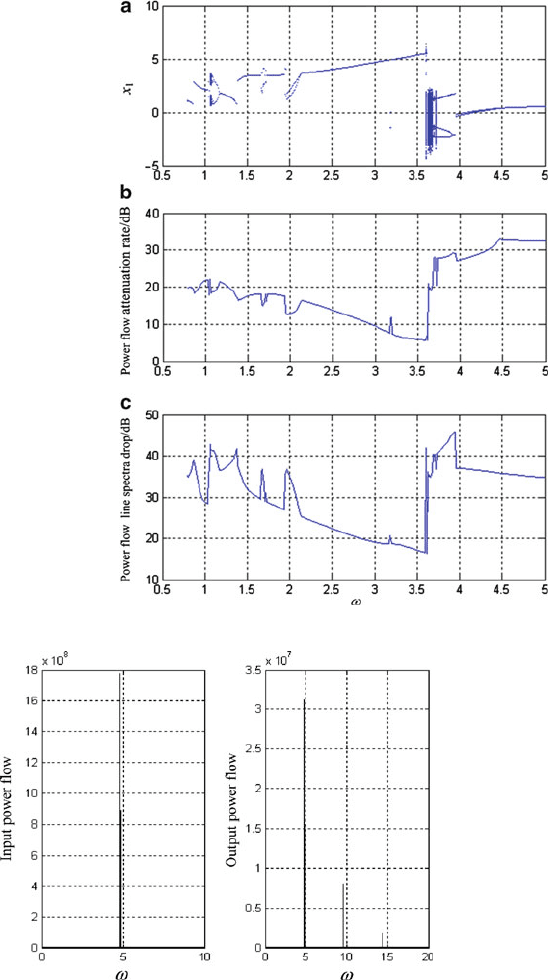
Fig. 6.9 Power flow
attenuation rate and line
spectra drop .f D 8:8,
! D .0:80 W 0:01 W 5//.
(a) Bifurcation diagram,
(b) power flow attenuation
rate, (c) power flow line
spectra drop
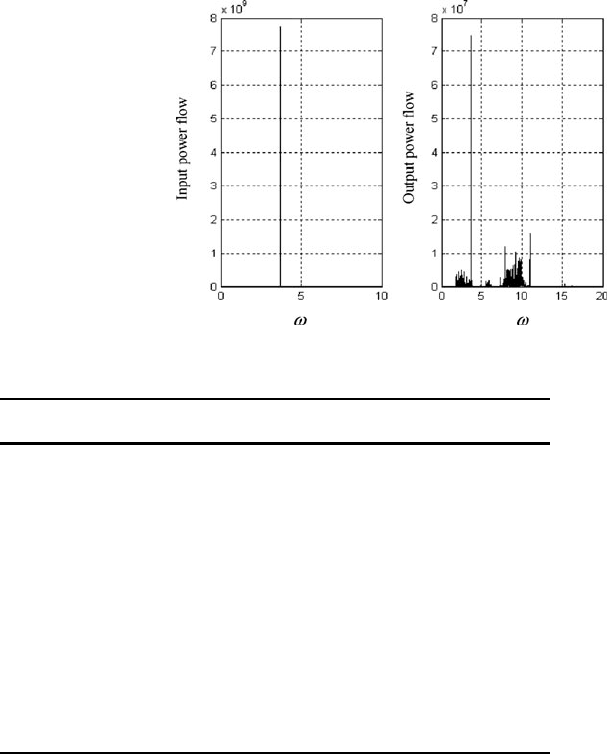
Fig. 6.10 Input and output power flow for P-1 motion .f D 8:8; ! D 4:80/
6 Two-Degree-of-Freedom Chaotic Vibration Isolation System 59
Fig. 6.11 Input and output
power flow for chaotic
motion .f D 8:8; ! D 3:70/
Table 6.1 Values of the PFAR and PFLSD at different excitation frequencies
No.
Excitation
frequency
Form
of motion
PFAR
(dB)
PFLSD at excitation
frequency (dB)
11.01 P1 21.92 36.69
2 1.06 Chaos 18.25 42.75
3 1.08 Chaos 18.62 41.45
41.09 P8 18.71 41.40
51.10 P4 18.73 41.40
61.12 P2 18.94 40.85
71.80 P1 18.06 28.16
82.07 P2 13.81 30.48
92.80 P1 11.35 20.20
10 3.70 Chaos 28.07 40.31
11 3.71 P8 27.98 40.45
12 3.74 P4 27.91 40.88
13 4.10 P2 28.07 36.82
14 4.80 P1 32.73 35.11
The dynamic behaviour distribution chart of the two-degree-of-freedom nonlin-
ear vibration isolation system is obtained, which shows that there exists complex
nonlinear behavior indeed in this system. Cascades of bifurcation in the two-degree-
of-freedom nonlinear vibration isolation system with different excitation amplitudes
are obtained.
The isolation effectiveness is analyzed from the point of view of energy. For
some parameters, the power flow attenuation rate in chaotic state is 17 dB higher
than that in P-1 state at best, and the power flow line spectrum drop in chaotic state
is 5–20dB higher than that in P-1 state.
60 J.-J. Lou et al.
It is also concluded that the isolation effectiveness of line spectrum is improved
after once or twice period-doubling bifurcation, when the power flow attenuation
rate and the power flow line spectrum drop are close to that in chaotic state.
To validate the effectiveness of the method of chaotic vibration isolation, the
vibration-isolation test rig with flexible foundation similar to the actual situation
onboard of ships is designed, and meticulous experiment is also accomplished.
Preliminary experimental results indicating better isolation in the chaotic regime
will be published in near future.
Acknowledgment This work was supported by National Natural Science Foundation of China
under Grant 50675220.
References
1. Kapitaniak T (1997) Chaos for engineers: theory, application, and control. Springer, London
2. Lou JJ, Zhu SJ, He L, et al (2005) Application of chaos method to line spectra reduction.
J Sound Vib 286:645–652
3. Lou JJ, Zhu SJ, He L, et al (2009) Experimental chaos in nonlinear vibration isolation system.
Chaos Solitons Fractals 40:1367–1375
4. Crede CE (1951) Vibration and shock isolation. Wiley, New York
5. Snowdon JC (1979) Vibration isolation use and characterization. J Acoust Soc Am
66:1245–1279
6. Ravindra B, Mallik AK (1993) Hard Duffing-type vibration isolator with combined coulomb
and viscous damping. Int J Non Linear Mech 28:427–440
7. Ravindra B, Mallik AK (1994) Performance of non-linear vibration isolation under harmonic
excitation. J Sound Vib 170:325–337
8. Long YJ, Wang CL, Zhang P (1998) Road roller based on chaotic theory. J China Agric Univ
3:19–22
9. Harris CM (1988) Shock and vibration handbook, 3rd edn. McGraw-Hill, New York
10. Karnopp DC (1995) Active and semi-active vibration isolation. J Sound Vib 117:177–185
11. Rivin EI (2003) Passive vibration isolation. The American Society of Mechanical Engineers,
New York
12. Lou JJ (2006) Application of chaos theory in line spectrum reduction [PHD dissertation]. Naval
University of Engineering, Wuhan

Chapter 7
Simulation and Nonlinear Analysis of Panel
Flutter with Thermal Effects in Supersonic Flow
Kai-Lun Li, Jia-Zhong Zhang, and Peng-Fei Lei
Abstract With the consideration of thermal effect, an improved panel flutter model
equation is established to study the dynamic behaviors of panel structures on super-
sonic aircrafts. The governing equation is approached by Galerkin Method, and then
the resulting ordinary differential equations of the panel are obtained. By the numer-
ical simulation, some essential nonlinear phenomena are discovered, and they play
an important role in the stability of the panel in supersonic flow. Finally, Mach num-
ber and Steady temperature recovery factor are considered bifurcation parameters,
Hopf bifurcation, and Pitchfork bifurcation, and other complex bifurcations at the
equilibrium points are analyzed in detail, respectively, by seeking the eigenvalues of
the Jacobian matrix of the dynamic system at bifurcation points. It can be concluded
that there exist a rich variety of nonlinear dynamics, and they are essential for the
stability of the panel in the supersonic flow.
7.1 Introduction
The panel structures have been used frequently on supersonic aircrafts. As the
aircrafts are flying at supersonic speed, the aerothermoelasticity has an enormous
impact on the aircrafts. Under the combined effects of aerodynamics, thermodynam-
ics, and structure dynamics, the panel structures on the aircrafts behave as periodic
oscillation, quasi-periodic oscillation, chaotic motion, buckling, etc. These phenom-
ena lead to a great deal of threat to the safety and life of the panel.
From the viewpoint of nonlinear dynamics, the states of panel varying from
static state to oscillation or dynamic buckling are the typical bifurcation behav-
iors, and such nonlinear phenomena could be utilized to improve the aerodynamic
J.-Z. Zhang (
)
School of Energy and Power Engineering, Xi’an Jiaotong University,
Xi’an, Shaanxi 710049, People’s Republic of China
e-mail: jzzhang@mail.xjtu.edu.cn
A.C.J. Luo (ed.), Dynamical Systems: Discontinuity, Stochasticity and Time-Delay,
DOI 10.1007/978-1-4419-5754-2
7,
c
Springer Science+Business Media, LLC 2010
61
62 K.-L. Li et al.
performance of the aircrafts. Therefore, using nonlinear theory to analyze the
stability of the panel is essential for the modern aerodynamic design.
Much of the early works have been devoted to panel flutter in supersonic speed
[1, 2]. And the nonlinear behavior of panel flutter has been discovered and inves-
tigated [3, 4]. Also the chaos theory has been introduced by several scholars to
investigate the panel flutter [5].
More recently, a panel flutter model with thermal effect has been established by
Gee and Sipcic [6]. The introduction of thermal effect makes the problem more com-
plicated. On the one hand, thermal effect reduces the stiffness of the panel because
of aerodynamic heating. On the other hand, thermal stress is generated because of
mismatch in the thermal expansion coefficients of panel and support structure. Also,
it has been found that the change of temperature distribution in the panel does not
synchronize with the change of temperature on the panel surface, that is, there is a
time-lag between them because of heat transferring.
An improved panel flutter model equation is established in this study, with the
consideration of thermal effects. In order to simplify the model equation, the re-
duction of panel stiffness and the time-lag of heat transferring are neglected. Von
Karman large deflection plate theory and Piston theory are used to obtain the strain
in the panel and aerodynamic loads respectively. Aerodynamic heating is obtained
from Busemann–Crocco’s solution of boundary layer equations.
By Galerkin method, the vector form of governing equation is obtained. And
then some nonlinear phenomena are discovered, and two main kinds of bifurcations
of the dynamic system are analyzed following the nonlinear theory.
7.2 Governing Equation
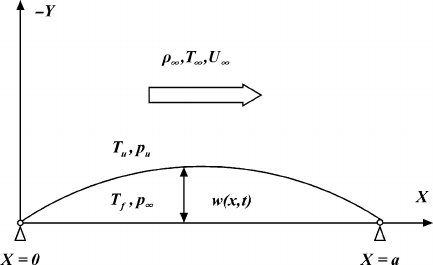
Figure7.1 is the schematic of two-dimensional panel with hinged boundary condi-
tion in supersonic flow. It is assumed that the panel is infinite in spanwise direction,
with a in length and h in thick.
Fig. 7.1 Two-dimensional panel with hinged boundary condition in supersonic flow
7 Analysis of Panel Flutter with Thermal Effects in Supersonic Flow 63
7.2.1 Dynamic Loads and Heating
The steady temperature in the panel caused by aerodynamic heating due to viscous
flow is obtained from Busemann–Crocco’s solution as follows [7],
T
f
D T
1
C R
f
Œ. 1/=2M
2
1
T
1
: (7.1)
According to Piston theory, the unsteady pressure on the outer surface of the panel
gives
p
u
D p
1
C .2q
1
=M
1
/D
t
w: (7.2)
From isentropic relation between pressure and temperature, the unsteady tempera-
ture change can be obtained from (7.2)
T
u
D T
1
C . 1/M
1
T
1
D
t
w: (7.3)
Actually, the temperature change on the outer surface is the result from viscous
flow and the compression and expansion of air, so the actual temperature on the
outer surface should be obtained by (7.1)and(7.3). Replacing T
1
in (7.3)byT
f
in (7.1), the actual unsteady temperature on the outer surface of the panel can be
written in the form
T
u
D T
f
C R
u
. 1/M
1
T
1
D
t
w: (7.4)
In the equations given above, D
t
w is defined by
D
t
w D V=U
1
D w
;x
C w
;t
=U
1
: (7.5)
As the panel is under flow at constant Mach number, then the temperature in the
inner side of panel maintains at the steady temperature T
f
due to viscous flow and
heat transferring. And the inner surface pressure on the panel is assumed to be equal
to the pressure p
1
, the pressure in the free stream.
7.2.2 Solution of Heat Transfer
The heat conduction along the thickness direction of the panel is governed by the
one-dimensional heat conduction equation. For this problem, Duhamel superposi-
tion integral is a closed-form solution [8], namely
T.z;t/D T
f
C
x
h
C
1
2
T
u
.t/
C
2
1
X
nD1
.1/
n
n
T
u
.0/C
Z
t
0
T
0
u
./e
n
2
d
e
n
2
t
sin n
x
h
C
1
2
; (7.6)

64 K.-L. Li et al.
T
u
D T
u
T
f
D R
u
. 1/M
1
T
1
D
t
w; (7.7)
D
ch
2
2
k
; (7.8)
where c
p
;
p
;h,andk
p
are the specific heat capacity, density, thickness, and thermal
conductivity of the panel, respectively. In fact, when aluminum alloy is adopted as
the material of the panel, will be far less than 1 due to small thickness of the panel
and good thermal conductivity of the material. So the distribution of temperature in
the panel can be simplified as
T.z;t/ D T
f
C
x
h
C
1
2
T
u
.t/: (7.9)
That means the time-lag of heat transferring can be neglected to get the approxi-
mation of the temperature distribution in the panel.
7.2.3 Governing Equations
The original governing equation of infinite two-dimensional panel flutter is
@
2
M
x
@x
2
C .N
x
C N
E
/
@
2
w
@x
2
C q.x;y/ D 0; (7.10)
where N
E
is an externally applied in-plane load and q.x; y/ is defined as
q.x; t/ D
p
h
@
2
w
@t
2
C .p
1
p
u
/: (7.11)
Introducing the thermal effect into Von Karman large deflection plate theory, the
stress in the panel gives
x
D
E
1
2
"
@u
@x
C
1
2
@w
@x
2
z
@
2
w
@x
2
.1 C /˛
p
T
p
#
; (7.12)
T
p
D T.x;t/ T
ref
; (7.13)
where T
p
denotes the difference between current temperature distribution and ini-
tial temperature distribution in the panel. In this study, it is assumed that
T
ref
D T
1
: (7.14)
And then the axial force and bending moment can be obtained as
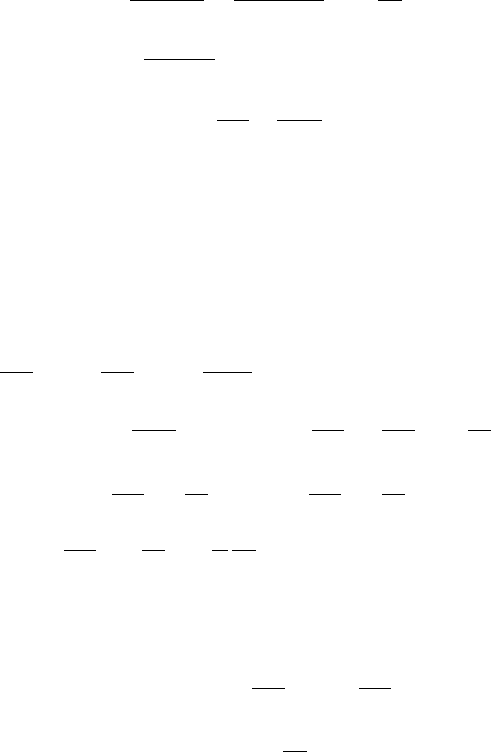
7 Analysis of Panel Flutter with Thermal Effects in Supersonic Flow 65
N
x
D
Eh˛
s
T
s
1
2
C
Eh
2a.1
2
/
Z
a
0
@w
@x
2
dx
˛
p
E
a.1 /
Z
a
0
dx
Z
h=2
h=2
T
p
dz; (7.15)
M
x
DD
@
2
w
@x
2
˛
p
E
1
Z
h=2
h=2
T
p
zdz; (7.16)
where T
s
is the difference between current temperature and initial temperature in
the support structure, it is defined as
T
s
D T
f
T
ref
: (7.17)
Substituting (7.11), (7.15), and (7.16) into the (7.10), and the nondimensional gov-
erning equation becomes
@
4
Nw
@ Nx
4
C ˆ
O
R
u
@
3
Nw
@ Nx
3
C ‚
O
R
u
@
3
Nw
@
N
t@Nx
2
C
12
O
R
f
1 C v
C 12
O
R
f
R
E
!
@
2
Nw
@ Nx
2
6
@
2
Nw
@ Nx
2
Z
1
0
@ Nw
@ Nx
2
d Nx
C6ˆ
O
R
u
@
2
Nw
@ Nx
2
Z
1
0
@ Nw
@ Nx
d Nx C 6‚
O
R
u
@
2
Nw
@ Nx
2
Z
1
0
@ Nw
@
N
t
d Nx
C
@
2
Nw
@
N
t
2
C ƒ
@ Nw
@ Nx
C ƒ
‚
ˆ
@ Nw
@
N
t
D 0: (7.18)
The coefficients in (7.18) are listed in Appendix 2. And the boundary condition of
(7.18)gives
Nw.0;
N
t/ DNw.1;
N
t/ D 0;
@
2
Nw
@ Nx
2
.0;
N
t/ D
@
2
Nw
@ Nx
2
.1;
N
t/ D 0; (7.19)
Nw. Nx; 0/ D g. Nx/;
@ Nw
@
N
t
. Nx;0/ D 0: (7.20)
7.2.4 Galerkin Method
Following Galerkin method, Nw can be denoted as
Nw. Nx;
N
t/ D
N
X
rD1
w
r
.
N
t/sin.r Nx/: (7.21)
Substituting (7.21)into(7.18) and integrating on the both side of the equation, the
ordinary differential equations are obtained as follows

66 K.-L. Li et al.
.s/
4
w
s
2
ˆ
O
R
u
N
X
rD1;r¤s
.r/
3
w
r
s
s
2
r
2
Œ1 .1/
sCr
‚
O
R
u
.s/
2
Pw
s
"
12
O
R
f
1 C v
C 12
O
R
f
R
E
#
.s/
2
w
s
C3.s/
2
w
s
N
X
rD1
.r/
2
w
2
r
6‚
O
R
u
.s/
2
w
s
N
X
rD1
Pw
r
Œ1 .1/
r
r
CRw
s
C2ƒ
N
X
rD1;r¤s
w
r
rs
s
2
r
2
Œ1 .1/
sCr
C ƒ
‚
ˆ
Pw
s
D 0; s D 1;:::;N: (7.22)
For the sake of simplicity, the resulting governing equations are rewritten in the
first-order form
Pw
s
D w
sCN
; Pw
sCN
Dba.s/w
s
bb.s/w
sCN
bc.s/w
sCN
N
X
rD1;r¤s
bf .s; r/w
r
N
X
rD1;r¤s
bg.s; r/w
s
w
2
r
N
X
rD1;r¤s
bh.s; r/w
s
w
rCN
N
X
rD1;r¤s
bi.s; r/w
r
bg.s; s/w
3
s
bh.s; s/w
s
w
sCN
: (7.23)
The coefficients in (7.23) are shown in Appendix 2. And the Jacobian matrix of the
dynamic system is
@ Pw
s
@w
s
D 0;
@ Pw
s
@w
r
D 0;
@ Pw
s
@w
sCN
D 1;
@ Pw
s
@w
rCN
D 0;
@ Pw
sCN
@w
s
Dba.s/
N
X
kD1;k¤s
bg.s; k/w
2
k
N
X
kD1;k¤s
bh.s; k/w
kCN
3bg.s; s/w
2
s
bh.s; s/w
sCN
;
@ Pw
sCN
@w
r
Dbf.s; r/ 2bg.s; r/w
s
w
r
bi.s; r/;
@ Pw
sCN
@w
sCN
Dbb.s/ bc.s/ bh.s; s/w
s
: (7.24)
7 Analysis of Panel Flutter with Thermal Effects in Supersonic Flow 67
Also, the equilibrium positions of the dynamic system can be obtained by solving
(7.25) as follows
bg.s; s/w
s
3
C ba.s/w
s
C
N
X
rD1;r¤s
bg.s; r/w
s
w
2
r
C
N
X
rD1;r¤s
Œbf.s; r/ C bi.s; r/w
r
D 0: (7.25)
Apparently, w
s
D 0; s D 1;:::;N are the equilibrium positions, and the stability
of this position is analyzed in the following section.
7.3 Numerical Results
In this section, it is assumed that R
u
D 0, that means only the impact of R
f
to the
panel is considered. Runge–Kutta Method is used to investigate the dynamic system.
When R
f
D 0 and R
f
D 0:056, the state of the panel changes from static state
to periodic oscillation respectively as the Mach number M
1
increases. And there
exist two main kinds of bifurcations as the system parameters are varied. Letting
M
1
D 2, the state of the panel changes from static state in original position to
buckling as the steady temperature recovery factor R
f
increases, the bifurcation is
also analyzed.
7.3.1 R
f
D 0, Mach Number as the Bifurcation Parameter
R
f
D 0 means that the thermal effects are not taken into account. From Figs. 7.2 and
7.3, it is can be found that the state of the panel changes from static state to periodic
oscillation as Mach number increases. As the parameters increase to the values as
follows:
R
f
D 0; M
1
D 6:03177; w
i
D 0; i D 1;:::;N;
the real parts of a pair of conjugate complex eigenvalues of the Jacobian matrix
equal to zero approximately and the real parts of the other eigenvalues are not equal
to zero, namely, the system is at a critical state. So as the Mach number increases
from 6.0317 to 6.0318, the Hopf bifurcation occurs in the dynamic system at about
M
1
D 6:03177. The bifurcation diagram is shown in Fig. 7.4.
