Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay
Подождите немного. Документ загружается.


Chapter 5
Complete Bifurcation Behaviors of a Henon Map
Albert C.J. Luo and Yu Guo
Abstract In this paper, a methodology to analytically predict the stable and
unstable periodic solutions for n-dimensional discrete dynamical systems is ap-
plied to investigate the Henon map. The positive and negative iterative mappings
of discrete maps are introduced for the mapping structure of the periodic solutions.
The complete bifurcation and stability of the stable and unstable periodic solutions
with respect to the positive and negative mapping structures is given. The Poincare
mapping sections of the Neimark bifurcation of periodic solutions is presented, and
the chaotic layers for the discrete system with the Henon map are observed.
5.1 Introduction
The Henon map in the discrete-time dynamic system was first introduced by Henon
[1] in 1976 to simplify the three-dimensional Lorenz equations as a Poincare map;
also, Henon observed chaos numerically in such a discrete system. These numeri-
cal results stimulated more attention on Henon map latter on. In 1979, Marotto [2]
mathematically proved the existence of chaotic behavior of Henon map for certain
parameters. Also, Curry [3] used Lyapunov characteristic exponent and frequency
spectrum to measure the chaotic behavior of Henon map. In 1988, Cvitanovic et al.
[4] investigated the topologic properties and multifractality of Henon map. In 1993,
Gallas [5] numerically investigated the parameter maps for Henon map. In 2000,
Zhusubaliyev et al. [6] did the bifurcation analysis of Henon map and further pre-
sented a more detailed parameter map. The aforementioned investigations were
based on the numerical computation. In 2005, Gonchenko et al. [7] discussed the
three-dimensional Henon map generated from a homoclinic bifurcation. In 2006,
Hruska [8] developed a numerical algorithm to model the dynamics of a polynomial
diffeomorphism of C
2
on its chain recurrent set and applied this algorithm to Henon
map. In 2007, Gonchenko et al. [9] studied the bifurcation of periodic solution of
A.C.J. Luo (
)
Department of Mechanical and Industrial Engineering, Southern Illinois University Edwardsville,
Edwardsville, IL 62026-1805, USA
e-mail: aluo@siue.edu
A.C.J. Luo (ed.), Dynamical Systems: Discontinuity, Stochasticity and Time-Delay,
DOI 10.1007/978-1-4419-5754-2
5,
c
Springer Science+Business Media, LLC 2010
37

38 A.C.J. Luo and Y. Guo
the generalized Henon map, and further proved the existence of infinite cascades
of periodic solutions in a generalized Henon map. In 2008, Lorenz [10] adopted a
random searching procedure to determine the parameter maps of periodic windows
embedded in chaotic solutions of Henon map. In 1992, Luo and Han [11]presented
a geometric approach to the period doubling bifurcation and multifractality of a
general one-dimensional iterative map. In 2005, Luo [12] investigated the mapping
dynamics of periodic motions in a nonsmooth piecewise system.
In this chapter, the method of mapping dynamics will be adopted to investigate
the bifurcation behavior of the Henon map. The stable and unstable periodic solu-
tions of the Henon map will then be investigated, and the eigenvalue analysis for
each periodic solution of the Henon map will be carried out; the parameter maps of
the Henon map can be obtained through analytical predictions which are beyond the
existing results.
5.2 Analysis
Consider the Henon map
f
1
.x
k
; x
kC1
; p/ D x
kC1
y
k
1 C ax
2
k
D 0
f
2
.x
k
; x
kC1
; p/ D y
kC1
bx
k
D 0
(5.1)
where x
k
D .x
k
;y
k
/
T
; f D .f
1
;f
2
/
T
and p D .a; b/
T
. Consider two positive and
negative mapping structures as
x
kCN
D P
.N /
C
x
k
D P
C
ıP
C
ı P
C
„ ƒ‚ …
N -terms
x
k
x
k
D P
.N /
x
kCN
D P
ıP
ı P
„ ƒ‚ …
N -terms
x
kCN
(5.2)
Equations (5.1)and(5.2)give
f.x
k
; x
kC1
; p/ D 0
f.x
kC1
; x
kC2
; p/ D 0
:
:
:
f.x
kCN 1
; x
kCN
; p/ D 0
9
>
>
>
=
>
>
>
;
(5.3)
and
f.x
kCN 1
; x
kCN
; p/ D 0
f.x
kCN 2
; x
kCN 1
; p/ D 0
:
:
:
f.x
k
; x
kC1
; p/ D 0:
9
>
>
>
=
>
>
>
;
(5.4)

5 Complete Bifurcation Behaviors of a Henon Map 39
The switching of equation order in (5.2)shows(5.3)and(5.4) are identical. For
periodic solutions for the positive and negative maps, the periodicity of the positive
and negative mapping structures of the Henon map requires
x
kCN
D x
k
or x
k
D x
kCN
(5.5)
So the periodic solutions x
kCj
.j D 0;1;:::;N/for the negative and positive map-
ping structures are the same, which are given by solving (5.3)and(5.5). However
the stability and bifurcation are different because x
kCj
varies with x
kCj 1
for the
j th positive mapping and x
kCj 1
varies with x
kCj
for the j th negative mapping.
For a small perturbation, (5.1) for the positive mapping gives
@f
@x
kCj 1
C
@f
@x
kCj
@x
kCj
@x
kCj 1
ˇ
ˇ
ˇ
ˇ
x
kCj 1
; x
kCj
D 0 (5.6)
where
@f
@x
kCj 1
x
kCj 1
; x
kCj
D
2
6
6
6
4
@f
1
@x
kCj 1
@f
1
@y
kCj 1
@f
2
@x
kCj 1
@f
2
@y
kCj 1
3
7
7
7
5
x
kCj 1
; x
kCj
D
"
2ax
kCj 1
1
b0
#
(5.7)
@f
@x
kCj
x
kCj 1
;x
kCj
D
2
6
6
6
4
@f
1
@x
kCj
@f
1
@y
kCj
@f
2
@x
kCj
@f
2
@y
kCj
3
7
7
7
5
x
kCj 1
; x
kCj
D
10
01
(5.8)
So one obtains
DP
C
x
kCj 1
D
@x
kCj
@x
kCj 1
x
kCj 1
D
@f
@x
kCj
1
@f
@x
kCj 1
x
kCj 1
D
"
2ax
kCj 1
1
b0
#
(5.9)
Similarly, for the negative mapping,
@f
@x
kCj
C
@f
@x
kCj 1
@x
kCj 1
@x
kCj
ˇ
ˇ
ˇ
ˇ
x
kCj 1
; x
kCj
D 0 (5.10)
40 A.C.J. Luo and Y. Guo
With (5.7)and(5.8), the foregoing equation gives
DP
.x
kCj
/ D
@x
kCj 1
@x
kCj
x
kCj
D
@f
@x
kCj 1
1
@f
@x
kCj
x
kCj
D
1
b
"
01
b2ax
kCj 1
#
(5.11)
Thus, the resultant perturbation of the mapping structure in (5.2)gives
ıx
kCN
D DP
.N /
C
x
k
D DP
C
DP
C
DP
C
„ ƒ‚ …
N -terms
ıx
k
ıx
k
D DP
.N /
ıx
kCN
D DP
DP
DP
„ ƒ‚ …
N -terms
ıx
kCN
(5.12)
where
DP
.N /
C
D
Q
N
j D1
DP
C
x
kCN j
DP
.N /
D
Q
N
j D1
DP
x
kCN j C1
9
=
;
(5.13)
Consider the eigenvalues
and
C
of DP
.N /
.x
kCN
/ and DP
.N /
C
.x
k
/, respectively.
The following statements hold.
1. If
ˇ
ˇ
C
1;2
ˇ
ˇ
<1(or
ˇ
ˇ
1;2
ˇ
ˇ
<1), the periodic solutions of P
.N /
C
.x
k
/ (or P
.N /
.x
kCN
/)arestable.
2. If
ˇ
ˇ
C
1 or 2
ˇ
ˇ
>1(or
ˇ
ˇ
1 or 2
ˇ
ˇ
<1), the periodic solutions of P
.N /
C
.x
k
/ (or P
.N /
.x
kCN
/) are unstable.
3. If real eigenvalues
C
1
D1 and
ˇ
ˇ
C
2
ˇ
ˇ
<1(or
1
D1 and
ˇ
ˇ
2
ˇ
ˇ
<1),
the period-doubling (PD) bifurcation of the periodic solutions of P
.N /
C
.x
k
/
(or P
.N /
.x
kCN
/) occurs.
4. If real eigenvalues
ˇ
ˇ
C
1
ˇ
ˇ
<1and
C
2
D 1 (or
ˇ
ˇ
1
ˇ
ˇ
<1and
2
D1), then
the saddle-node (SN) bifurcation of the periodic solutions relative to P
.N /
C
.x
k
)
(or P
.N /
.x
kCN
/) occurs.
5. If two complex eigenvalues of
ˇ
ˇ
C
1;2
ˇ
ˇ
D 1.or
ˇ
ˇ
1;2
ˇ
ˇ
D 1/, the Neimark bifurca-
tion (NB) of the periodic solutions of P
.N /
C
.x
k
/ (or P
.N /
.x
kCN
/) occurs.
5.3 Illustrations
A numerical prediction of the periodic solutions of the Henon map is presented
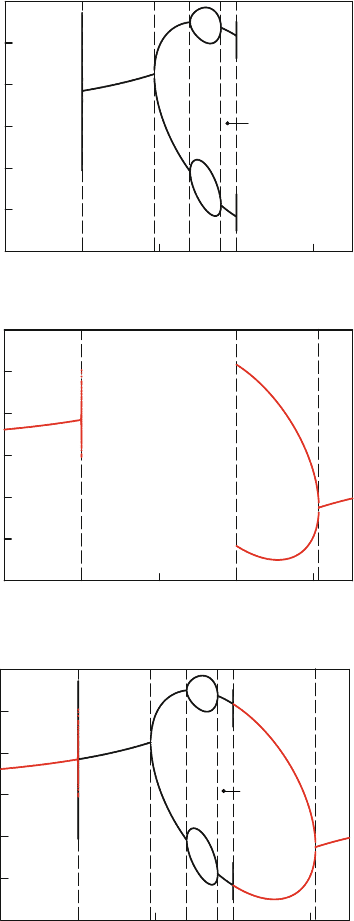
with varying parameter b for a D 0:85, as shown in Fig. 5.1. The dashed vertical
lines give the bifurcation points. The acronyms “PD,” “SN,” and “NB” represent the
5 Complete Bifurcation Behaviors of a Henon Map 41
a
NB
PD
NB
SN
PD
SN
PD
SN
P
+
(2)
P
+
(2)
P
+
P
+
(4)
P
+
(2)
P
+
(2)
P
+
(4)
Parameter, b
Iterative Points, x
k
−1.5
−1.0
−.5
0.0
.5
1.0
1.5
−2 −10 1 2
NBNB
PD
SN
P
−
P
−
(2)
P
−
(2)
P
−
Parameter b
Parameter b
Iterative Points, x
k
−1.5
−1.0
−.5
0.0
.5
1.0
1.5
−1
−2
012
−1
−2
012
Iterative Points, x
k
−1.5
−1.0
−.5
0.0
.5
1.0
1.5
NB
PD
P
+
NB
SN
PD
SN
PD
SN
PD
SN
P
−
P
−
b
c
Fig. 5.1 Numerical predictions of periodic solutions of the Henon mapping: (a) positive mapping
.P
C
/,(b) negative mapping .P
/ and (c) combination of the negative and positive mappings
.a D 0:85/
42 A.C.J. Luo and Y. Guo
period-doubling bifurcation, saddle-node bifurcation and Neimark bifurcation, re-
spectively. It is observed that the stable periodic solutions for positive mapping P
C
lie in b 2 .1:0; 1:0/. The stable period-1 solution of P
C
is in b 2 .1; 0:074/.
At b D1, the Neimark bifurcation (NB) of the period-1 solution occurs. At
b 0:074, the period-doubling bifurcation (PD) of the period-1 solution oc-
curs. This point is the saddle-node bifurcation (SN) for the period-2 solution of P
C
(i.e., P
.2/
C
). The periodic solution of P
.2/
C
is in the range of b 2 .0:074; 0:3935/
and b 2 .0:82; 1:0/. Also, there is a periodic solution of P
.4/
C
existing in the range
of b 2 .0:3935; 0:82/.Atb D 1, the Neimark bifurcation (NB) of P
.2/
C
occurs.
After the Neimark bifurcation, the stable periodic solutions for positive mapping
P
C
do not exist any more. Such stable periodic solutions for positive mapping
P
C
isshowninFig.5.1a. The stable solution for negative mapping P
is in the
ranges of b 2 .1; 1:0/ and b 2 .1:0; C1/.Atb D1, the Neimark bifurca-
tion (NB) of the period-1 solution of P
occurs. The period-1 solution of P
is in
b 2 .1; 1:0/ and b 2 .2:0735; C1/. The period-doubling bifurcation (PD) of
the period-1 solution of P
occurs at b 2:0735, and the bifurcation point is the
saddle-node bifurcation (SN) for the period-2 solution of P
(i.e., P
.2/
). The stable
periodic solution of P
.2/
is in b 2 .1:0; 2:0735/.Atb D 1, the Neimark bifur-
cation (NB) of the periodic solution of P
.2/
occurs. Such stable periodic solutions
for positive mapping P
are shown in Fig. 5.1b. The total bifurcation scenario for
positive and negative mappings is plotted in Fig. 5.1c. The parameter ranges are in
b 2 .1; C1/.
From the numerical prediction, the stable periodic solutions of the Henon map
are obtained. Herein, through the corresponding mapping structures, the stable and
unstable periodic solutions for positive and negative mappings of the Henon maps
are represented in Figs. 5.2 and 5.3. The acronyms “PD,” “SN,” and “NB” represent
the period-doubling bifurcation, saddle-stable node bifurcation, and Neimark bifur-
cation, respectively. The acronyms “UPD,” “USN” represent the period-doubling
bifurcation relative to unstable nodes and saddle-unstable node bifurcation, re-
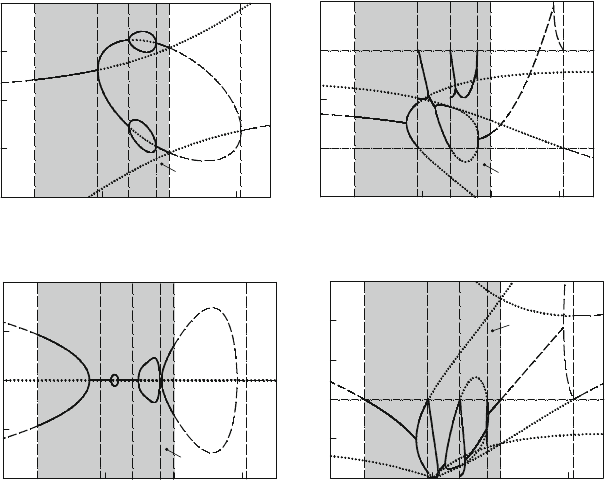
spectively. The analytical prediction of stable and unstable periodic solutions of
positive mapping P
C
for a D 0:85 and b 2 .1; C1/ is presented in Fig. 5.2a–
d. The periodic solution of the positive mapping is arranged in Fig. 5.2a. The
real and imaginary parts and magnitude of eigenvalues for such periodic solutions
are given in Fig. 5.2b–d, respectively. The stable periodic solutions for positive
mapping P
C
lie in b 2 .1:0; 0:0745/, which is closer to numerical predic-
tion. In other words, the stable period-1 solution of P
C
is in b 2 .1; 0:0745/.
For b 2 .0:0745; 0:39555/, the unstable period-1 solution of P
C
is saddle. For
b 2 .1; 1:0/, the unstable period-1 solution of P
C
is relative to the unstable
focus. The corresponding bifurcations are Neimark bifurcation (NB) and period-
doubling bifurcation (PD). However, another period-1 solution of P
C
exists and
which is unstable. For b 2 .2:07244; C1/, the periodic solution is of the unstable
node. However, for b 2 .1; 2:07244/, the periodic solution is relative to saddle.
Thus, the unstable period-doubling bifurcation (UPD) of the period-1 solution of
P
C
occurs at b 2:07244. At this point, the unstable periodic solution is from an
5 Complete Bifurcation Behaviors of a Henon Map 43
PD
NM
SN
NM
PD
SN
Parameter, b
−1
012
Iteration Points, x
k
−2
−1
0
1
2
P
+
(2)
P
+
(4)
P
+
(2)
P
+
PD
SN
UPD
USN
PD
NM
SN
NM
PD
SN
Parameter, b
−101 2
Real Part of Eigenvalue, Re
λ
1,2
−
2
−
1
0
1
2
P
+
(2)
P
+
(4)
P
+
(2)
P
+
PD
SN
UPD
USN
PD
NM
SN
NM
PD
SN
Parameter, b
Imaginary Part of Eigenvalue, Im
λ
1,2
−
2
−
1
0
1
2
P
+
(2)
P
+
(4)
P
+
(2)
P
+
PD
SN
UPD
USN
PD
NM
SN
NM
PD
SN
Parameter, b
012
012
Magnitude of Eigenvalue, |
λ
1,2
|
0.0
0.5
1.0
1.5
2.0
2.5
P
+
(2)
P
+
(4)
P
+
(2)
P
+
PD
SN
UPD
USN
a
b
c
d
−1
−1
Fig. 5.2 Analytical predictions of stable and unstable periodic solutions for positive mapping
.P
C
/ of the Henon map: (a) periodic solutions, (b) real part of eigenvalues, (c) imaginary part of
eigenvalues and (d) magnitude of eigenvalues (a D 0:85 and b 2 .1; C1/)
unstable node to saddle. Because of the unstable period-doubling bifurcation, the
unstable periodic solution of P
.2/
C
for the unstable node is obtained for b 2
.1:0; 2:07244/. This unstable periodic solution is from unstable focus to unstable
node during the parameter of b 2 .1:0; 2:07244/.Atb 2:07244, the bifurcation
of the unstable periodic solution of P
.2/
C
occurs between the saddle and unstable
node. This bifurcation is called the unstable saddle-node bifurcation. The unstable
periodic solution of P
.2/
C
relative to saddle exists for b 2 .0:3955; 0:8190/, while
the stable period-4 solution of P
.4/
C
occur on the same interval. At b 0:3955,
there is a period doubling bifurcation, where the P
.2/
C
periodic solution becomes
unstable and P
.4/
C
periodic solution starts. At b 0:8190, there is a saddle node bi-
furcation where the P
.4/
C
periodic solution goes into the P
.2/
C
solution. At b D 1:0,
the Neimark bifurcation (NB) between the periodic solutions of P
.2/
C
relative to the
unstable and stable focuses occurs. The stable periodic solution of P
.2/
C
is existing
for b 2 .0:0745; 0:3955/ and b 2 .0:8190; 1:0/.
44 A.C.J. Luo and Y. Guo
UPD
NM
USN
NM
PD
SN
Parameter, b
Iteration Points, x
k
−
2
−
1
0
1
2
P
−
P
−
(2)
P
−
UPD
USN
UPD
USN
UPD
NM
USN
NM
PD
SN
Parameter, b
Parameter, b
Parameter, b
Real Part of Eigenvalue, Re
λ
1,2
−
2
−
1
0
1
2
UPD
USN
P
−
P
−
(2)
P
−
UPD
USN
NMNM
PD
SN
Imaginary Part of Eigenvalue, Im
λ
1,2
−
15
−
10
−
5
0
5
10
15
UPD
USN
P
−
P
−
(2)
P
−
UPD
USN
UPD
USN
UPD
NM
USN
NM
PD
SN
−1 −1
−1 −1
201
012
012
012
Magnitude of Eigenvalue, |
λ
1,2
|
0.0
0.5
1.0
1.5
2.0
2.5
UPD
USN
P
−
P
−
(2)
P
−
UPD
USN
ab
cd
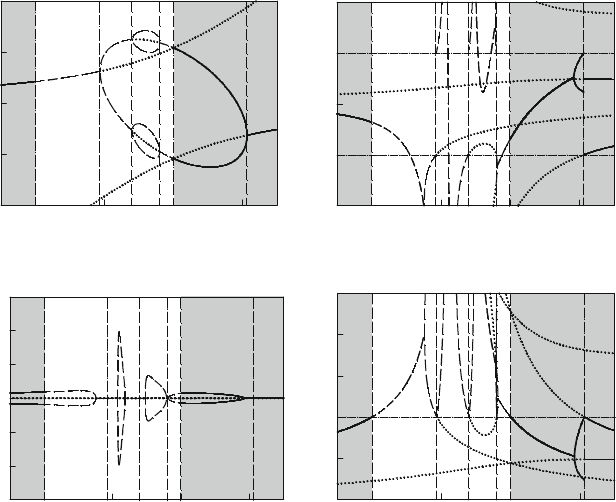
Fig. 5.3 Analytical predictions of stable and unstable periodic solutions for negative mapping
.P
/ of the Henon map: (a) periodic solutions, (b) real part of eigenvalues, (c) imaginary part of
eigenvalues and (d) magnitude of eigenvalues (a D 0:85 and b 2 .1; C1/)
Similarly, the analytical prediction of stable and unstable periodic solutions of
negative mapping P
for a D 0:85 and b 2 .1; C1/ is presented in Fig. 5.3a–d.
The periodic solution of the negative mapping is plotted in Fig. 5.3a. The real part,
and imaginary part and magnitude of the eigenvalues for such periodic solutions
are presented in Fig. 5.3b–d, respectively. The stable periodic solutions for positive
mapping P
lie in b 2 .1; 1:0/ and b 2 .1:0; C1/, which is the same as in
numerical prediction. The stable period-1 solution of P
is stable focuses in b 2
.1; 1:0/ and stable nodes in b 2 .2:07244; C1/.Forb 2 .1:0; 0:0745/,
the unstable period-1 solution of P
is from the unstable focus to unstable node. At
b D1, the bifurcation between the stable and unstable period-1 solution of P
is the Neimark bifurcation (NB). For b 2 .0:0745; C1/, the unstable period-1
solution of P
is of the saddle. Thus, the bifurcation between the period-1 solution
of P
between the unstable node and saddle occurs at b D0:0745,whichis
called the unstable period-doubling bifurcation (UPD). For b 2 .0:0745; 0:3955/
and b 2 .0:8190; 1:0/, the unstable period-2 solution of P
(i.e., P
.2/
) exists. For
b 2 .1:0; 2:07244/, the stable period-2 solution of P
(i.e., P
.2/
) is from the stable
5 Complete Bifurcation Behaviors of a Henon Map 45
focus to the stable nodes. Thus, the point at b 0:3955 is the bifurcation of the
unstable periodic solution of P
.2/
, which is the unstable saddle-node bifurcation
between the unstable node and saddle (i.e., USN).
For the point at b D 1, the Neimark bifurcation between the periodic solutions of
P
.2/
relative to the unstable and stable focuses occurs. The point at b 2:07244 is
the bifurcation of the stable periodic solution of P
.2/
, which is the saddle-node
bifurcation between the stable node and saddle (SN). For b 2 .1; 2:07244/,
the unstable period-1 solution of P
is saddle. At b 2:07244, the period-
doubling bifurcation (PD) of the period-1 solution of P
takes place. Also for
b 2 .0:3955; 0:8190/, there exists the unstable period-4 solution of P
.4/
,which
is again saddle.
From the analytical prediction, the observations can be stated as follows.
1. The stable periodic solution of positive mapping P
C
is the unstable periodic
solution of negative mapping P
.
2. The stable periodic solution of negative mapping P
is the unstable periodic
solution of positive mapping P
C
.
3. The PD and SN bifurcations of the periodic solutions of positive mapping P
C
are the UPD and USN bifurcations of the periodic solutions of negative mapping
P
,viceversa.
4. The PD and SN bifurcations of the periodic solutions of negative mapping P
are the UPD and USN bifurcations of the periodic solutions of positive mapping
P
C
,viceversa.
5. If the unstable periodic solutions of positive mapping P
C
are saddle, the corre-
sponding periodic solutions of negative mapping P
are also saddle.
In addition, the Neimark bifurcation between the periodic solution relative to the
unstable and stable focuses is of great interest. The Poincare mapping relative to
the Neimark bifurcation of the period-1 solution of positive mapping (or negative
mapping) at a D 0:85 and b D1 is presented in Fig. 5.4a. The most inside
point
x
k
;y
k
.0:4237; 0:4237/ is the point for the period-1 solution of P
C
or P
relative to the Neimark bifurcation. For the specified parameters, the initial
values of .x
k
;y
k
/ used for simulation are given in Table 5.1. The most outside curve
with the initial condition
x
k
;y
k
.1:0597; 0:4237/ is the biggest boundary for
the strange attractors around the period-1 solutions with the Neimark bifurcation.
The skew symmetry of the strange attractors in the Poincare mapping section is
observed.
The Poincare mapping relative to the Neimark bifurcation of the period-2 solu-
tion of positive mapping (or negative mapping) at a D 0:85 and b D 1 is presented
in Fig. 5.4b. The two points
x
k
;y
k
.1:0846; 1:0846/ and .1:0846; 1:0846/
are the points for the period-2 solution of P
C
or P
relative to the Neimark bi-
furcation. For the specified parameters, the input data for initial values are listed
in Table 5.2. with the outer chaotic layer, the strange attractor near the periodic
solutions of P
.2/
C
-1 (or P
.2/
-1) disappears.

46 A.C.J. Luo and Y. Guo
Fig. 5.4 Poincare mappings
at the Neimark bifurcation of
the Henon map: (a) period-1
(i.e., P
C
-1 or P
-1)
(a D 0:85 and b D 1)and
(b) period-2 solution
(i.e., P
.2/
C
-1 or
P
.2/
-1)(a D 0:85 and b D 1)
Iterative Coordinates x
k
−0.5 0.0 0.5 1.0 1.5
Iterative Coordinates y
k
−1.5
−1.0
−0.5
0.0
a
b
0.5
Iterative Coordinates
x
k
−1.2 −0.9 0.9 1.2
Iterative Coordinates y
k
−1.2
−0.9
0.9
1.2
Table 5.1 Input data
for Poincare mappings
.x
k
;y
k
/.x
k
;y
k
/
.0:4237; 0:4237/ .0:7037; 0:4237/
.0:4737; 0:4237/ .0:8037; 0:4237/
.0:5537; 0:4237/ .0:9037; 0:4237/
.0:6237; 0:4237/ .1:0597; 0:4237/
Table 5.2 Input data
for Poincare mappings
.x
k
;y
k
/.x
k
;y
k
/
.1:1728; 1:0846/ .1:1128; 1:0846/
.1:1541; 1:0846/ .1:0939; 1:0846/
.1:1328; 1:0846/ .1:0846; 1:0846/
5.4 Conclusion
In this chapter, a discrete dynamical system of the Henon map was investigated. The
positive and negative iterative mappings of discrete maps were employed for the
mapping structure of the periodic solutions. The complete bifurcation and stability
