Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay
Подождите немного. Документ загружается.

27
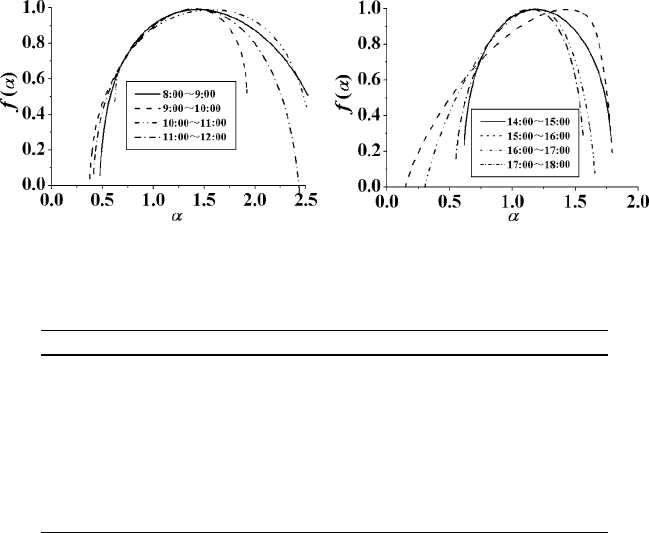
Fig. 3.1 Multifractal spectrum for real network traffic
Table 3.1 Multifractal spectrum parameters for real sequence
Date ˛
min
f.˛
min
/˛
max
f.˛
max
/˛ f
8–9 0.4731 0.0576 2.7137 0.04 2.2406 0.0176
9–10 0.3743 0.0381 1.9223 0.5211 1.548 0.483
10–11 0.6201 0.4739 2.6183 0.0415 1.9982 0.4324
11–12 0.4121 0.0659 2.4348 0 2.0227 0.0659
14–15 0.6153 0.2371 1.7835 0.2675 1.1682 0.0304
15–16 0.1481 0 1.7947 0.1957 1.6466 0.1957
16–17 0.3031 0 1.6556 0.077 1.3525 0.077
17–18 0.5515 0.1595 1.5614 0.2913 1.01 0.1318
f D f.˛
min
/ f.˛
max
/
In particular, the multifractal spectrum width during 17:00 to 18:00 is the narrowest,
and the width during 8:00 to 9:00 is the widest, that means the latter shows the most
non-uniform property of its network traffic. During 15:00 to 16:00, both ˛
min
and
the f.˛
min
/ are minimum, that implies the probability of occurrence of maximum
traffic is lowest, and however the traffic is sensitive to the breaking. On the other
hand, during 10:00 to 11:00, both ˛
min
and f.˛
min
/ are maximum, then the prob-
ability of occurrence of maximum traffic is highest, and the traffic is difficult to
become bursting and breaking. During 9:00 to 10:00, the f.˛
max
/ is the maximum
one, that means the probability of occurrence of minimum is the highest one. On
the contrary, during 11:00 to 12:00, the f.˛
max
/ is minimum, that is, the probability
of occurrence of minimum is lowest. Furthermore, it is clear that the shape of the
multifractal spectrum depends on f significantly, namely, its positive and nega-
tive value. For example, there exists a hooked-curve on the left of the multifractal
spectrum during 10:00 to 11:00, and a hooked-curve on the right of the multifrac-
tal spectrum during 9:00 to 10:00. This is the results from the emergence of the
maximum and minimum flow ratio of the probability, that is, when f > 0, proba-
bility of the maximum traffic is greater than the probability of the minimum traffic,
and vice versa.
3 Multifractal Spectrum of LAN Traffic
28 Y. Liu and J.-Z. Zhang
3.4.2 Relationship Between Multifractal Spectrum Parameters
and Traffic Variation
From the simulation analysis given above, the multifractal spectrum parameters
˛ and f can describe the fluctuation of the network traffic to some extent. For
analyzing the relationship between the multifractal spectrum and variation of the
traffic further, Z
i
is introduced to measure the variation of average flux I.t
i
/ in a
certain time interval t,
Z
i
D ln
I.t
i
/
I.t
i1
/
: (3.10)
Time scale t is set to 1 h, then I.t
i
/ denotes the average flux of the i-instant traffic,
I.t
i
1/ means the i 1-instant average flux, so that there are a set of parameters,
Z
i
;˛
i
and f
i
, at each instant.
The time sequence collected during 15:00 pm on March 15, 2006 to 10:00 am on
March 28, 2006, a total of 307 h, and the variation of ˛
i
;f
i
vs. Z
i
are shown
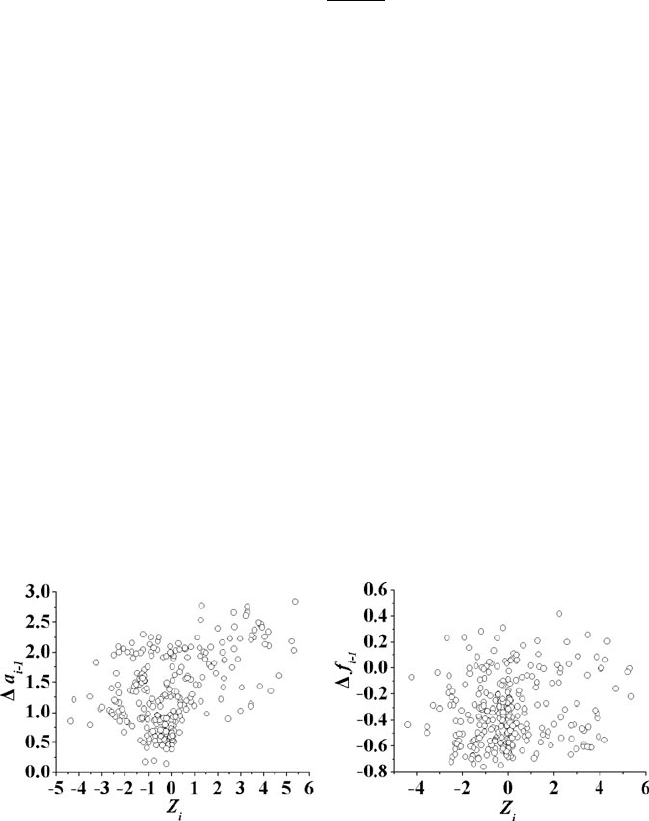
in Fig. 3.2. It is clear that ˛
i
will become greater as Z
i
is farther away from the
origin, that is, greater the changes in traffic is, greater the ˛
i
becomes. At the same
time, as jZ
i
j is small, the probability of large jf
i
j larger becomes higher, that
indicates there exists a relationship between the multifractal spectrum parameters
and the average flow.
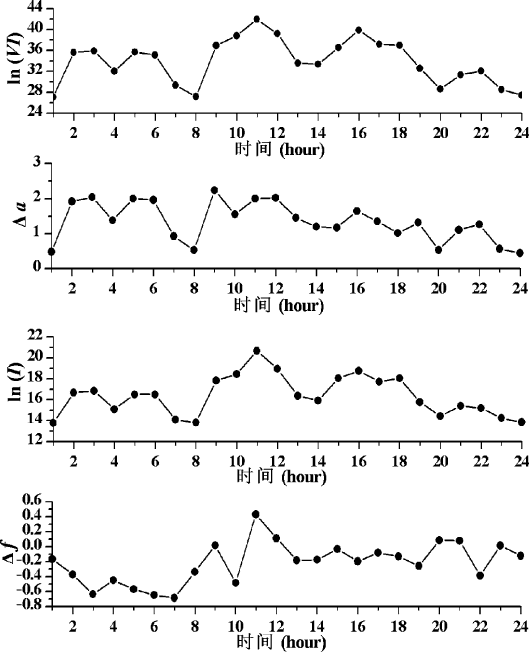
In addition, Fig. 3.3 is the time history of the variance ln.VI/; ˛, the average
flux rate ln(I )andf , for the time sequence collected on March 16, 2005. It is
clear that the variation of ˛ is very similar to that of variance ln.VI/,andthere
are five lowest points in the time history of ln(I ); they are 3:00 to 4:00, 7:00 to
8:00, 13:00 to 14:00, 16:00 to 17:00, and 19:00 to 20:00. And there are also seven
lowest points in the time history of f , they are 2:00 to 3:00, 6:00 to 7:00, 9:00 to
10:00, 12:00 to 13:00, 15:00 to 16:00, 18:00 to 19:00, and 21:00 to 22:00. It can be
seen, except two time intervals, the occurrence of the lowest points in the other time
intervals of f lags that of ln(I ) for an hour. Once such phenomena is available for
all of the network traffic, f can be chosen as a measure to predict the system, and
the relationship will be investigated in depth, that is the next work.
Fig. 3.2 The distribution of Z
i
vs. ˛
i
and f
i
29
Fig. 3.3 The time history of variance ln.VI/; ˛, the average flux rate ln(I )andf
3.5 Concluding Remarks
The results show that the multifractal spectrum could describe the complex bursting
and breaking behaviors for the local area network traffic, and can be considered
a method for studying the complex nonlinear phenomena for the network system.
Moreover, it is proved that there exists local singularity in the network traffic after
the analysis of the real local area network traffic in detail. In particular, the important
relationship between the multifractal spectrum and the variation of the traffic is
founded and established. As a conclusion, all of the results presented can be applied
to the prediction of traffic, deign, and performance evaluation, and play an important
role for the network traffic.
3 Multifractal Spectrum of LAN Traffic
30 Y. Liu and J.-Z. Zhang
References
1. Levy VJ, Sikdar B (2001) A multiplicative multifractal model for TCP traffic [J]. In: IEEE
symposium on computers and communications-proceedings, pp 714–719
2. Feldmann A, Gilbert AC, Willinger W (1998) Data networks as cascades: investigating the mul-
tifractal nature of internet WAN traffic [J]. Comput Commun Rev 28(4):42–55
3. Lacovoni G, Mance V, Verqni D (2000) Single source TCP behaviour: a multifractal analysis,
conference record [J]. In: IEEE global telecommunications conference, vol 1, pp 323–328
4. Feldmann A, Gilbert AC, Willinger W, et al (1998) The changing nature of network traffic:
scaling phenomena [J]. ACM SIGCOMM Comput Commun Rev 28(2):5–29
5. Jackson JK (1957) Network of waiting lines [J]. Oper Res 5:518–521
6. Beran J, Sherman R, Taqqu MS, et al (1995) Long-range dependence in variable-bit-rate video
traffic [J]. IEEE Trans Commun 43(2):1566–1579
7. Rao Y, Xu Z, Liu Z (2004) Length requirement of self-similar network traffic [J]. Chin J Electron
13(1):175–178
8. Riedi R (1995) An improved multifractal formalism and self-similar measures [J]. J Math Anal
Appl 189:462–490

Chapter 4
A Boundary Crisis in High Dimensional
Chaotic Systems
Ling Hong, Yingwu Zhang, and Jun Jiang
Abstract A crisis is investigated in high dimensional chaotic systems by means
of generalized cell mapping digraph (GCMD) method. The crisis happens when
a hyperchaotic attractor collides with a chaotic saddle in its fractal boundary, and
is called a hyperchaotic boundary crisis. In such a case, the hyperchaotic attractor
together with its basin of attraction is suddenly destroyed as a control parameter
passes through a critical value, leaving behind a hyperchaotic saddle in the place
of the original hyperchaotic attractor in phase space after the crisis, namely, the
hyperchaotic attractor is converted into an incremental portion of the hyperchaotic
saddle after the collision. This hyperchaotic saddle is an invariant and nonattract-
ing hyperchaotic set. In the hyperchaotic boundary crisis, the chaotic saddle in the
boundary has a complicated pattern and plays an extremely important role. We also
investigate the formation and evolution of the chaotic saddle in the fractal boundary,
particularly concentrating on its discontinuous bifurcations (metamorphoses). We
demonstrate that the saddle in the boundary undergoes an abrupt enlargement in its
size by a collision between two saddles in basin interior and boundary.
4.1 Introduction
A hyperchaotic attractor is typically defined as chaotic behavior with at least
two positive Lyapunov exponents. Such an attractor is common in high dimen-
sional chaotic systems, namely at least two-dimensional maps or four-dimensional
flows [1, 2]. The first example of a hyperchaotic attractor was presented in the
folded-towel map and the 4-D R¨ossler system [3]. The experimental realization
of hyperchaotic behavior was first observed in an electronic circuit [4]. There
have been reports of chaos–hyperchaos transition in a driven system [5]andin
a 9D model for a Rayleigh–B´enard convection [6]. The transition from chaos to
hyperchaos is a blowout bifurcation [7] which occurs when a chaotic attractor lying
L. Hong (
)
MOE Key Lab for Strength and Vibration, School of Aerospace, Xi’an Jiaotong University,
Xi’an 710049, People’s Republic of China
e-mail: hongling@mail.xjtu.edu.cn
A.C.J. Luo (ed.), Dynamical Systems: Discontinuity, Stochasticity and Time-Delay,
DOI 10.1007/978-1-4419-5754-2
4,
c
Springer Science+Business Media, LLC 2010
31
32 L. Hong et al.
in some symmetric subspace becomes transversely unstable. Blowout bifurcations
are related to some interesting complex phenomena such as chaotic synchroniza-
tions [8], riddle basins, on-off intermittency, [9] and metamorphoses of chaotic
saddle for high dimensional chaotic systems [10].
Crises of chaotic attractors are extremely common and have been observed in an
experiment [11]. Sudden changes in chaotic attractors with parameter variation have
been called crises [12,13]. Crises are due to a collision of chaotic attractors with an
unstable periodic orbit, in which chaotic attractors undergo sudden discontinuous
changes. Three types of crisis can be distinguished according to the nature of the
discontinuous change that the crisis induces in the chaotic attractor: in the first type,
a chaotic attractor is suddenly destroyed as the parameter passes through its critical
value; in the second type, the size of the attractor in phase space suddenly increases;
in the third type, two or more chaotic attractors merge to form one chaotic attractor.
The crises of hyperchaotic attractors reported here are a high-dimensional chaotic
phenomenon, whereas to our knowledge, few works dealing with this problem have
been published to date.
A generalized cell-mapping digraph (GCMD) method for global analysis of non-
linear systems was first introduced by Hsu [14]. Later, the GCMD method was
developed [15] and has been used to deal with crisis bifurcations for determinis-
tic and noisy nonlinear systems [16–18].
The current chapter studies a sudden change in a hyperchaotic attractor with
two positive Lyapunov exponents. Such a change is called a hyperchaotic crisis fol-
lowing Grebogi’s definition of crisis in low dimensional chaotic systems [12, 13].
We shall study a hyperchaotic crisis involving the collision of a hyperchaotic at-
tractor with a chaotic saddle in its fractal boundary. The origin and evolution of
the chaotic saddle in the boundary are also investigated, particularly concentrating
on its discontinuous bifurcations (metamorphoses). We illustrate this hyperchaotic
crisis event by Kawakami map.
The reminder of the chapter is outlined as follows. In Sect. 4.2, we study a hy-
perchaotic boundary crisis in Kawakami map. The chapter concludes in Sect. 4.3.
4.2 A Hyperchaotic Boundary Crisis in a Kawakami Map
The model presented here is a map given by
x.n C 1/ Dax
n
C y
n
y.n C 1/ D x
2
n
b: (4.1)
The equation is well known as Kawakami map. It was first introduced by
Kawakami and Kobayashi in 1979 for an endomorphism study [19]. The strange hy-
perchaotic dynamics of the Kawakami map was thoroughly studied for a parameter
region of 0:1 a 0:15, b D 1:6 [20, 21] including a hyperchaotic attractor
with two Lyapunov exponents and unstable invariant sets in its basin boundary.
In the present chapter, we confirm the previously reported results and further find
4 A Boundary Crisis in High Dimensional Chaotic Systems 33
a hyperchaotic boundary crisis involving the collision of a hyperchaotic attractor
with a chaotic saddle in its fractal boundary. And we also investigate the origin
and evolution of the chaotic saddle in the fractal boundary, particularly focusing on
its discontinuous bifurcations (metamorphoses). To our knowledge, no attempt has
been made regarding this problem.
The domain D D
f
2:5 x 2:5; 2:0 y 3:5
g
is discretized into
300 300 cells when applying the FGCM method, 10 10 sampling points are
used within each cell.
We fix the parameter b D 1:6 and allow the parameter a to vary from 0:1 to 0:22.
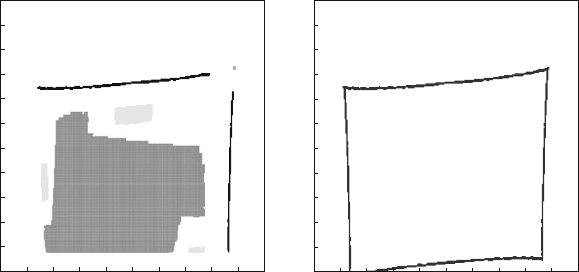
When a D 0:1, there exist a hyperchaotic attractor and three unstable solutions
including a chaotic saddle in the basin interior as well as a saddle with two narrow
disjointed strips and a unstable node embedded in the boundary. The global phase
portrait is shown in Fig. 4.1. We reassure the above results by refining the 300
300 cell structure to 800 800 through 500 500. Grey denotes the hyperchaotic
attractor. Light grey denotes the chaotic saddle in the basin interior. Black denotes
the saddle in the boundary. The circle symbol ı denotes the unstable node in the
boundary. The boundary is shown in (b) of figures. The color coding and symbol
hold throughout the chapter.
As a increases, the chaotic saddle in the basin interior becomes bigger and closer
to the boundary. A discontinuous bifurcation (metamorphosis) happens in the in-
terval a 2 .0:1648; 0:1649/. In the case, the chaotic saddle is touching the saddle
in the boundary when a D 0:1648, creating a chaotic saddle in a fractal boundary
when a D 0:1649. The chaotic saddle in the fractal boundary has a complicated
structure and plays an extremely important role in an upcoming hyperchaotic cri-
sis. Namely, it will collide with the hyperchaotic attractor when a increases further
to 0:2164, leading to a hyperchaotic boundary crisis. The global phase portrait is
shown in Figs. 4.2 and 4.3
when a D 0:1648 and a D 0:1649.
a
b
x
y
x
y
−2.5 −2 −1.5 −1 –0.5 0 0.5 1 1.5 2 2.5
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
3.5
−2.5 −2 −1.5 −1 −0.5 0 0.5 1 1.5 2 2.5
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
3.5
Fig. 4.1 Global phase portrait of the Kawakami map with a D 0:1, b D 1:6. Grey denotes the
hyperchaotic attractor. Light grey the chaotic saddle in the basin interior. Black the saddle in the
boundary. The circle symbol ı the unstable node in the boundary. The boundary is shown in (b)

34 L. Hong et al.
ab
x
y
−2.5 −2 −1.5 −1 −0.5 0 0.5 1 1.5 2 2.5
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
3.5
x
y
−2.5 −2 −1.5 −1 −0.5 0 0.5 1 1.5 2 2.5
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
3.5
Fig. 4.2 Just before the discontinuous bifurcation for the Kawakami map with a D 0:1648,
b D 1:6 at a collision between two saddles, light grey one in the interior and black one in the
boundary. The color coding is the same as that in Fig. 4.1
a
b
x
y
−2.5 −2 −1.5 −1 −0.500.511.522.5
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
3.5
y
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
3.5
x
−2.5 −2 −1.5 −1 −0.5 0 0.5 1 1.5 2 2.5
Fig. 4.3 Just after the discontinuous bifurcation for the Kawakami map with a D 0:1649, b D 1:6
creating a chaotic saddle in a fractal boundary. The color coding is the same as that in Fig. 4.1
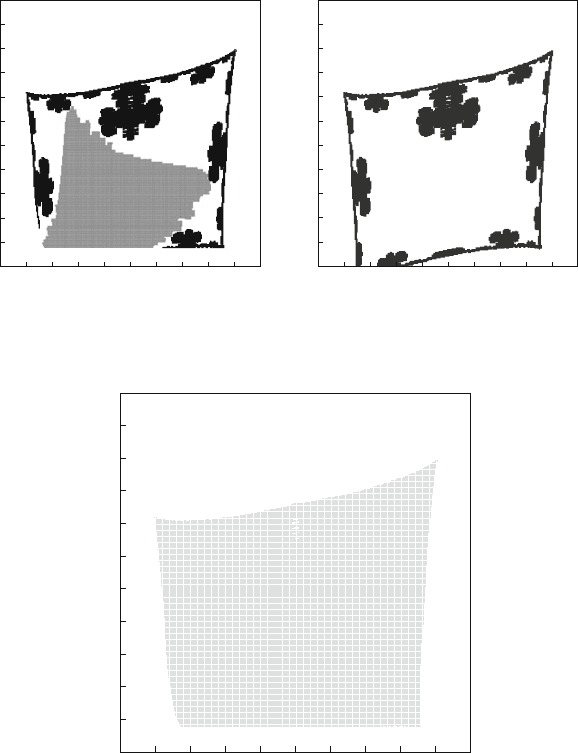
A hyperchaotic crisis occurs in the interval a 2 .0:2164; 0:2165/ when the hy-
perchaotic attractor collides with a chaotic saddle in its fractal boundary. In the case,
the hyperchaotic attractor together with its basin of attraction is suddenly destroyed
as a control parameter passes through a critical value, leaving behind a hyperchaotic
saddle in the place of the original hyperchaotic attractor in phase space after the
crisis, namely, the hyperchaotic attractor is converted into an incremental portion
of the hyperchaotic saddle after the collision. This hyperchaotic saddle is an in-
variant and nonattracting hyperchaotic set. The global phase portraits are shown
in Figs. 4.4 and 4.5.
4 A Boundary Crisis in High Dimensional Chaotic Systems 35
x
x
y
−2.5 −2 −1.5 −1 −0.5 0 0.5 1 1.5 2 2.5
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
3.5
y
−2.5 −2 −1.5 −1 −0.5
0 0.5 1 1.5 2 2.5
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
3.5
ab
Fig. 4.4 Just before the hyperchaotic crisis for the Kawakami map with a D 0:2164, b D 1:6
when the hyperchaotic attractor touches the chaotic saddle in the fractal boundary. The color coding
is the same as that in Fig. 4.1
x
−2.5 −2 −1.5 −1 −0.5 0 0.5 1 1.5 2 2.5
y
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
3.5
Fig. 4.5 Just after the hyperchaotic crisis for the Kawakami map with a D 0:2165, b D 1:6
leaving behind the hyperchaotic saddle
4.3 Concluding Remarks
In this chapter, we have investigated hyperchaotic crises, where a hyperchaotic
attractor collides with a chaotic saddle on its fractal boundary. In the case, the
hyperchaotic attractor together with its basin of attraction is suddenly destroyed as a
control parameter passes through a critical value, leaving behind a hyperchaotic sad-
dle in the place of the original hyperchaotic attractor in phase space after the crisis.
36 L. Hong et al.
A collision with a chaotic saddle in a fractal boundary is the typical mechanism by
which hyerchaotic attractors can be suddenly destroyed. In the hyperchaotic crises,
the chaotic saddle in the boundary has a complicated pattern and plays an extremely
important role. We also investigate the formation and evolution of the chaotic saddle
in the fractal boundary, particularly concentrating on its discontinuous bifurcations
(metamorphoses). We demonstrate that the saddle in the boundary undergoes an
abrupt enlargement in its size by a collision between two saddles in basin interior
and boundary.
Acknowledgments This work is supported by the National Science Foundation of China under
Grant Nos. 10772140 and 10872155 as well as the Scientific Research Foundation for the Returned
Overseas Chinese Scholars, State Education Ministry.
References
1. Baier G, Klein M (1990) Maximum hyperchaos in generalized Henon map. Phys Lett A
151:281–284
2. Baier G, Sahle S (1995) Design of hyperchaotic flows. Phys Rev E 51:R2712–R2714
3. Rossler OE (1979) An equation for hyperchaos. Phys Lett A 71:155–157
4. Matsumoto T, Chua LO, Kobayashi K (1986) Hyperchaos: laboratory experiment and numeri-
cal confirmation. IEEE Trans Circuits Syst CAS-33(11):1143–1147
5. Kapitaniak T, Thylwe KE, Cohen I, Wjewoda J (1995) Chaos–hyperchaos transition. Chaos
Solitons Fractals 5(10):2003–2011
6. Reiterer P, Lainscsek C, Schurrer F (1998) A nine-dimensional lorenz system to study high-
dimensional chaos. J Phys A 31:7121–7139
7. Kapitaniak T, Maistrenko Y, Popovych S (2000) Chaos–hyperchaos transition. Phys Rev E
62(2):1972–1976
8. Kapitaniak T (2005) Chaos synchronization and hyperchaos. J Phys: Conf Ser 23:317–324
9. Ott E, Sommerer JC (1994) Blowout bifurcations: the occurrence of riddled basins and on–off
intermittency. Phys Lett A 188:39–47
10. Kapitaniak T, Lai YC, Grebogi C (1999) Metamorphosis of chaotic saddle. Phys Lett A
259(6):445–450
11. Ditto WL, Rauseo S, Cawley R, Grebogi C (1989) Experimental observation of crisis-induced
intermittency and its critical exponent. Phys Rev Lett 63:923–926
12. Grebogi C, Ott E, Yorke JA (1982) Chaotic attractors in crisis. Phys Rev Lett 48:1507–1510
13. Ott E (2002) Chaos in dynamical systems. Cambridge University Press, Cambridge
14. Hsu CS (1995) Global analysis of dynamical systems using posets and digraphs. Int J Bifurcat
Chaos 5(4):1085–1118
15. Hong L, Xu JX (1999) Crises and chaotic transients studied by the generalized cell mapping
digraph method. Phys Lett A 262:361–375
16. Hong L, Xu JX (2001) Discontinuous bifurcations of chaotic attractors in forced oscillators by
generalized cell mapping digraph (GCMD) method. Int J Bifurcat Chaos 11:723–736
17. Hong L, Sun JQ (2006) Codimension two bifurcations of nonlinear systems driven by fuzzy
noise. Physica D: Nonlinear Phenom 213(2):181–189
18. Xu W, He Q, Fang T, Rong H (2004) Stochastic bifurcation in Duffing system subject to har-
monic excitation and in presence of random noise. Int J Non-Linear Mech 39:1473–1479
19. Kawakami H, Kobayashi O (1976) Computer experiment on chaotic solution. Bull Fac Eng
Tokushima Univ 16:29–46
20. He DH, Xu JX, Chen YH (1999) A study on strange dynamics of a two dimensional map. Acta
Physica Sin 48(9):1611–1617
21. He DH, Xu JX, Chen YH (2000) Study on strange hyper chaotic dynamics of kawakami map.
Acta Mechanica Sin 32(6):750–754
