Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay

Подождите немного. Документ загружается.

78 B.C. Gegg et al.

steady state motion. The eccentricity frequency and amplitude with initial con-

ditions yield a steady state solution that can be characterized by the switching

components characteristics; three measures are introduced. The typical character-

ization of a steady state response is noted by the magnitude of the displacement and

velocity components at a zero phase measure of the system [3]. In a similar manner,

one of the new parameters introduced herein is the magnitude of the displacement

and velocity state in each principal direction. A new quantity, referred to as MAG.,

is multiplied by the minimum of the switching force product (MFP) components

(MAG and MFP will be formally be deﬁned herein). This unique measure in combi-

nation with the MAG. is a ﬁrst application in literature. Additionally, the complexity

is further quantiﬁed by the recording the total number of mappings (NOM), which

is also a ﬁrst application in literature. Due to varying dimensions of complexity in

this system, combinations of the NOM, MFP, and MAG. are necessary to fully un-

derstand what phenomena may be inducing complex motion. Applications of these

ideas and measures are not limited to machining. Rather, any system which contains

boundaries in their continuous systems can be modeled by discontinuous systems

theory. The ultimate implications of this study are the development of switching

components and their use within a control scheme to produce a speciﬁc type of sta-

bility in a discontinuous system. If such switching components can be monitored

in experiment, a control scheme can be adopted to manipulate these components to

avoid such an interaction [4]. However, if the goal is to continually interact with a

boundary, then avoidance of a sink boundary, or in this case a chip seizure can be

completed. As far as this study is concerned, the modeling of a machine tool with-

out control is adopted to observe the natural reaction of a system, which indeed will

point out the requirement of such an approach to achieve robust operation.

8.2 Structured Motions by the Mapping Technique

The mechanical model of 8.1 (A, B) is described by the chip adhesion dynamics,

.x; t; 

/ D 0: .CAD/ (8.1)

CAD denotes chip adhesion dynamics. The dynamics of the tool with no work-piece

contact are

.x; t; 

/ D 0: .TD/ (8.2)

TD denotes tool-piece dynamics. The dynamics of a reducing chip length pro-

cess are

.x; t; 

/ D 0: .NC/ (8.3)

NC denotes tool and work-piece dynamics, no cutting. The dynamics of an increas-

ing chip length process are

.x; t; 

/ D 0: .CRC/ (8.4)

8 A Parameter Study of a Machine Tool with Multiple Boundaries 79

CRC denotes tool and work-piece dynamics with cutting and reducing chip length.

The dynamics are

.x; t; 

/ D 0: .CIC/ (8.5)

CIC denotes tool and work-piece dynamics with cutting and increasing chip length.

Parameters deﬁning .

for i D 0; 1; 2; 3; 4/ the dynamics of (8.1–8.5) repre-

sent such characteristics such as mass, stiffness, damping, etc. In any case of the

dynamics deﬁned within these domains and on the boundaries, the interactions of

these systems with the domain boundaries can be clearly understood by discon-

tinuous systems theory of Luo [5]. The state of the tool is measured through the

. Nx; Ny/ representing the tangential and normal directions with respect to contact of

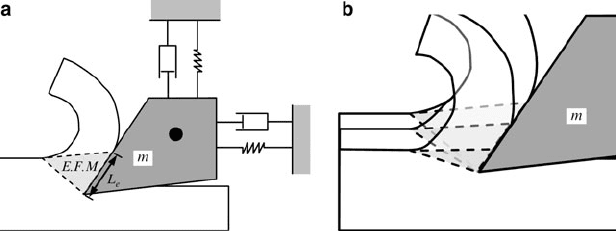
the work-piece (Figs. 8.1 and 8.2). Since the focus of the chip interactions are ap-

plied to the tool rake surface, the . Nx; Ny/ coordinate system is transformed to the

. Qx; Qy/ coordinate system,







cos ˛ sin ˛

sin ˛ cos ˛





D ƒ





: (8.6)

(

)

(

)

(

)

Fig. 8.1 Cutting tool mechanical model: (a) external forces, (b) mechanical analogy

(

,V,t

)

⋅

(

,V,t

)

Fig. 8.2 Periodic

intermittent cutting motions

in the phase plane

80 B.C. Gegg et al.

The initial contact boundary of the tool and work-pieces is

CNx/sin ˇ C .Y

 Y

Ny/ cos ˇ D ı

: (8.7)

Such a boundary is related to the measure

. Nx; Ny/ D .X

CNx/sin ˇ C .Y

 Y

Ny/ cos ˇ  ı

: (8.8)

The onset of cutting boundary is

CNy/ sin ˛ C .X

 X

Nx/ cos ˛ D ı

: (8.9)

The ﬁnal boundary is considered the chip disappearance boundary; where the chip

begins to reduce in length until no effective force transmission is made through the

chip-tool interface,

Qy

/ DQy.x;y/; (8.10)

where L

is the chip length, Qy

is the initial tool position at the switching point

on the chip-tool rake surface friction boundary, and Qy is the tool position at time t

(see Fig. 8.3). x D .x; Px/

and y D .y; Py/

. The normalized governing equations

characteristic of each domain or Eqs. (8.1–8.5) are of the form

r.t/ C ƒ

1

.i/

gƒ

r.t/ C ƒ

1

.i/

gƒ

r.t/ D ƒ

.i/

cos.t/ C b

.i/

t C c

.i/

;

(8.11)

where

r D . Qx; Qy/

. The damping, stiffness, periodic amplitude and constants noted

in Eq. (8.11) are deﬁned in the appendix.

Fig. 8.3 Chip and tool-piece: (a) effective force contact and (b) route to loss of effective force

contact

8 A Parameter Study of a Machine Tool with Multiple Boundaries 81

8.3 Domains and Boundaries

The four domains considered in this study are noted to overlap in several areas, and

a formal comprehensive deﬁnition is necessary as in Gegg [6, 7].Domain1isthe

vibration of the tool-piece without contacting the work-piece,

†

.x; y; Px; Py/ Df.x; y; Px; Py/jD

.x; y/ 2 .0; 1/gI (8.12)

domain 2 is the contact of the tool and work-piece without cutting,

†

.x; y; Px; Py/ D

(

.x; y; Px; Py/ jD

.x; y/ 2 .1;0/

;

.x; y; Px; Py/ jD

.x; y/ 2 .0; 1/

;

(8.13)



.x; y; Px; Py/jD

.x; y/ 2 .1; 1/

and .x; y; Px; Py/jD

.x; y/ 2 .1;0/



if .x; y; Px; Py/j

Qy. Px; Py/ 2 .1;V/I

;

(8.14)

domain 3 exists purely during reduced chip length,

†

.x; y; Px; Py/ D

.x; y; Px; Py/jD

.x; y/ 2 .1;0/g;

.x; y; Px; Py/jD

.x; y/ 2 .1;0/g;

.x; y; Px; Py/jD

.x; y/ 2 .0; L

/g;

.x; y; Px; Py/j

Qy. Px; Py/ 2 .1;V/gI

;

(8.15)

and domain 4 is well deﬁned by normal cutting,

†

.x; y; Px; Py/ D

.x; y; Px; Py/jD

.x; y/ 2 .1;0/;

.x; y; Px; Py/jD

.x; y/ 2 .1;0/;

.x; y; Px; Py/j

Qy. Px; Py/ 2 .V; 1/:

;

(8.16)

The boundaries created by the domains noted in the above equations are

@†

.x; y; Px; Py/ Df.x; y; Px; Py/j'

.x; y/ D '

.x; y/ D D

.x; y/ D 0g; (8.17)

@†

.x; y; Px; Py/ D

(

.x; y; Px; Py/j'

.x; y/ D '

.x; y/ D D

.v/ D 0 if

Qy.Px; Py/ > V;

.x; y; Px; Py/j'

. Px; Py/ D

Qy.Px; Py/ V D 0 if D

.x; y/ < 0;

)

(8.18)

@†

D .x; y; Px; Py/j'

.x; y; Px; Py/ D

(

.x; y/ D 0 if D

.x; y/ < 0;

.x; y/ D 0 if

Qy.Px; Py/ < V;

(8.19)

and

@†

D .x; y; Px; Py/j'

. Px; Py/ D '

. Px; Py/ D

Qy. Px; Py/  V D 0 if D

.v/<0;

(8.20)

82 B.C. Gegg et al.

as in Gegg [6, 7]; where V D

V= and  is the eccentricity frequency applied

to the work-piece. The discontinuous systems theory will now be applied to this

machine-tool through the state and domain deﬁnitions.

8.4 Motion Switch Ability Conditions

Development of the switching conditions is determined by application of discontin-

uous systems theory as in Gegg et al. [8,9]. Accordingly, the only boundary which

has the potential to produce a sink boundary is the chip-tool friction boundary as

deﬁned herein. The force conditions governing the passage of motion through the

boundary of (8.3)are

.3/

y;t/F

.4/

y;t/ > 0on @†

(passable motion); (8.21)

.3/

y;t/F

.4/

y;t/  0 on @†

(non-passable motion): (8.22)

Appearance/disappearance of passable/non-passable motion,

.3/

y;t/F

.4/

y;t/  0 on @†

: (8.23)

The boundary @†

is notation referring to the chip-tool friction boundary. The

forces noted in (8.21) are derived from the state and the total forces acting on the

tool-piece; hence,

.i/

y;t/ D F

.i/

y;t/ D

.i/

.t/ DRx

.i/

sin ˛ CRy

.i/

cos ˛: (8.24)

The friction boundary exhibiting completely passable vector ﬁelds is deﬁned by

.3/

y;t/ > 0; F

.4/

y;t/ >0on @†

; (8.25)

which implies,

.3/

y;t/F

.4/

y;t/ > 0on @†

: (8.26)

The non-passable motion through the friction boundary has switching components

.3/

y;t/ > 0; F

.4/

y;t/ <0on @†

; (8.27)

which implies,

.3/

y;t/F

.4/

y;t/ < 0on @†

; (8.28)

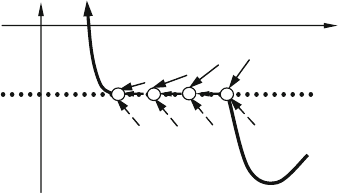
8 A Parameter Study of a Machine Tool with Multiple Boundaries 83

Fig. 8.4 Vector ﬁelds for

passable and non-passable

with appearance and

vanishing points a speciﬁc

example

(

)

⋅

(

)

Observe the simulation of Fig. 8.4. The boundary is initially non-passable, but

becomes passable after motion along the boundary; where the vector ﬁeld changes

direction. Boundary four, the chip reduction boundary, is a permanently passable

boundary as noted by Gegg et al. [10–12].

8.5 Parameter Study of (e, )

Consider the periodic motion,

D P

ı P

: (8.29)

This motion structure implies that two switching points exist which deﬁnes a solu-

tion set. Since there are two switching points, there are two switching force products.

Hence,

.1/

D F

.3;1/

.4;1/

;

.2/

D F

.3;2/

.4;2/

)

(8.30)

The force components for this particular case are deﬁned by domains three and four.

The boundary of these two domains is the chip/tool friction boundary. As a result

of limiting the output of the parameter study to one output for two input variables,

only one of the force products can be shown on a contour or three-dimensional

ﬁgure. A zero force product is known to be a predictive measure of the system

encountering a change in the motion structure; hence, the minimum absolute value

of the switching force products is recorded as the single output for the contour and

three-dimensional ﬁgures. In general, the force components are

min

D min



.k/



D min



.i;k/

.j;k/



; (8.31)

where i and j are the domains bordering the chip/tool friction boundary, and k is the

kth switching force product for the steady state motion of the machine-tool system.

84 B.C. Gegg et al.

Furthermore, the magnitude of the minimum absolute value force product and the

orbit in the phase plane with respect to the switching points is a useful output.

Hence,

Mag.e; / D min.jFP

.k/

.ı Qx

C .ı Qy

C .ı

; (8.32)

where

ı Qx

D max. Qx

/  min. Qx

ı Qy

D max. Qy

/  min. Qy

D max.

/  min.

D max.

/  min.

;

(8.33)

for m; n; p; q; r; s; u; v 2 Œ1; w. The parameter w is the total number of switching

points in the periodic orbit. Hence, max. Qx

/ is the maximum value of Qx out of the w

switching points and so on for the remaining measures of (8.33). Consider the steady

state motion of a machine-tool where the above measures are recorded for a two

parameter .e; / range allowing contouring and three-dimensional mesh plotting of

the minimum force product component and the magnitude of the phase orbit. The

parameters of most traditional reference in a parameter map are the frequency and

amplitude. The related parameters in this study are the eccentricity frequency  and

amplitude e. The dynamical system parameters for the following results are

D 10

D 740 Ns=mm;d

D 630 Ns=mm;

D k

D 560 kN=mm;k

D 1 MN=mm;

D 100 kN=mm;d

D d

D 0 Ns=mm;

and the external force and geometry parameters are

D ı

D 10

3

m;D 0:7; L

D 1:0  10

4

m;VD 20 mm=s;

˛ D



rad;ˇD 0:1 rad;D



rad;

D Y

D 10

3

m;X

D Y

D 5  10

3

The minimum force product noted in (8.31) are shown in the form of a contour

plot in Fig. 8.5a, where the color variation is determined on a logarithmic scale. The

three-dimensional view of a mesh plot is shown in Fig.8.5b, where the minimum

force product (MFP) is shown to vary with eccentricity amplitude and frequency,

.e; /; respectively. The use of the logarithmic scale is necessary for both the

MFP and the MAG (magnitude of (8.32)). Hence, the contour plot of Fig.8.5a

maintains the largest MFP in the neighborhood of the natural frequency groups

of this machine-tool. The most useful components of Fig. 8.5aarethedarkest

areas, which imply the potential for chip seizure motion. There are apparent dis-

continuities in the contour plot which denotes a grazing of the chip/tool friction

boundary. This phenomena causes the steady state of the machine-tool to jump to

a new orbit with an MFP of zero or nearly zero. Although the MFP, Fig. 8.5a, b,

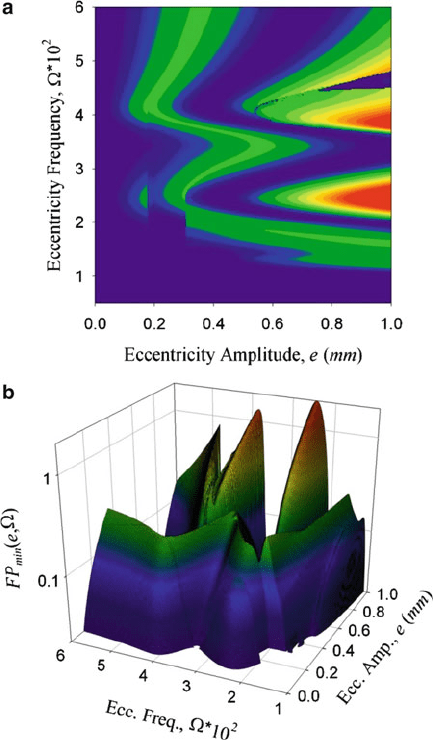
8 A Parameter Study of a Machine Tool with Multiple Boundaries 85

Fig. 8.5 Minimum force product study for a machine-tool undergoing steady state motion

with eccentricity amplitude e vs. eccentricity frequency :(a) ContourŒe;  D min.FP

.k/

(b)min.FP

.k/

/ vs:evs:for L

D 1.mm/

uncovers the areas in the eccentricity amplitude and frequency .e; / range where

chip seizure may occur, this says nothing about what motion actually occurs. Hence,

the total number of mappings or domains traversed in steady state motion is recorded

in a contour plot of Fig. 8.6a. The lighter colors denote the maximum number of

mappings recorded (w D 30 for the current results). The three-dimensional mesh

plot of the number of mappings is shown in Fig. 8.6b. The number of mappings in

the steady state solution structure is very clearly noted in Fig. 8.6b. The level of

mappings noted by the number one is the motion of the tool when there is no in-

teraction with the chip/tool friction boundary. The noticeable jumps in the mesh are

the areas that have an increased number of mappings which then denote increased

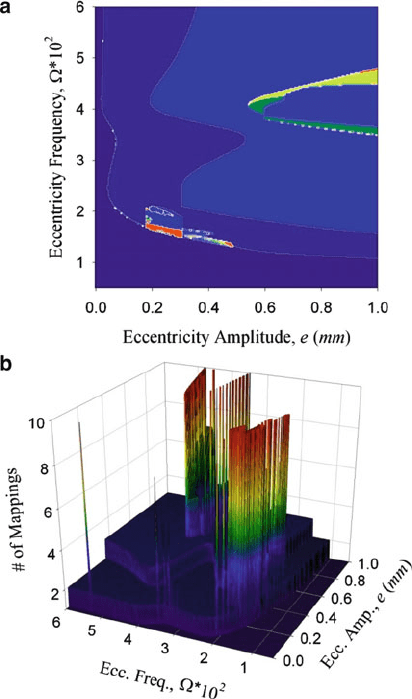
86 B.C. Gegg et al.

Fig. 8.6 Number of mappings in steady state motion for a machine-tool undergoing steady state

motion with eccentricity amplitude e vs. eccentricity frequency ,forL

D 1.mm/

complexity in the system. A combination of the MFP and the NOM (number of

mappings) will provide perhaps the most useful method of determining whether the

chip seizure motion is occurring in the potential neighborhoods; see Fig. 8.7a. There

are four notable areas that are bordered by the NOM’s outline. Region A is that

near the second natural frequency group, where a chip seizure motion occurs in the

steady state motion. The remaining regions (labeled by B) outlined by the NOM

are grouped nearest the ﬁrst natural frequency group. Such motions are expected

to have chip seizure in the steady state structure with associated grazing motions.

Furthermore, the use of the magnitude of the delta measure (MAG) and the MFP

is useful to show the growth and reduction of the phase orbit in several planes, see

Fig. 8.7b.

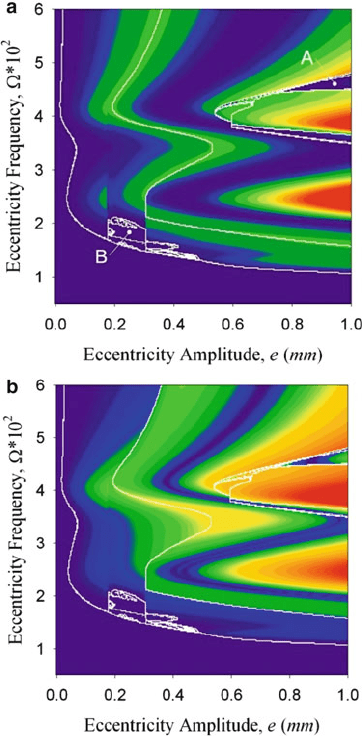
8 A Parameter Study of a Machine Tool with Multiple Boundaries 87

Fig. 8.7 Number of mappings overlaid on (a) minimum force product and (b) magnitude for

a machine-tool undergoing steady state motion with eccentricity amplitude e vs. eccentricity

frequency ,forL

D 1.mm/

8.6 Numerical Prediction of Eccentricity Frequency 

As a result of the parameter study of Figs. 8.5–8.7, interest of the phase and speciﬁc

switching force components is developed. Hence, the numerical prediction of steady

state motion for this machine-tool is shown via switching phase mod.t

;2/ and

displacement Qy.Dy

/,Fig.8.8a, b; respectively. The range of eccentricity frequency

 2 Œ50:0; 600:0.rad=s/ is studied with the parameters,

e D 0:275 mm and L

D 1:0 mm: