Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay
Подождите немного. Документ загружается.

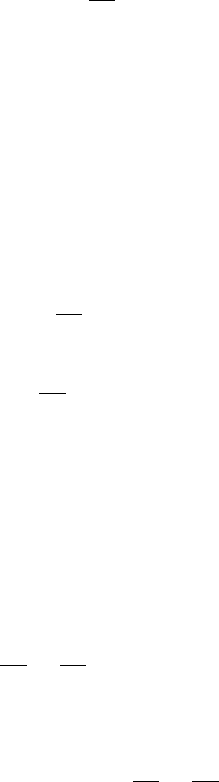
12 Control of Systems with Time Delay 139
12.2.2 Continuous Time Approximation
Consider a nonlinear system with one time delay given by,
P
x D f .x .t / ; x .t /;t/CBu .t/ ; (12.15)
where x 2 R
n
; u 2 R
m
, f is a nonlinear function of its arguments, and B DfB
ij
g is
the control influence matrix. Following the idea of semi-discretization, we discretize
the delayed part of the state vector .x .t t
1
/;0 < t
1
/.LetN be an integer
such that D =N.
i
D i .i D 1;2;:::;N/. We introduce a finite forward
difference approximation of the derivatives of .x .t
i
/;1 i N/as
P
x .t
i
/ D
1
Œx .t
i1
/ x .t
i
/ : (12.16)
Note that other approximation schemes including, for example, the central differ-
ence and Gear integration method for ordinary differential equations, can be used,
and that the discretization of the time delay interval can be nonuniform.
Define M D n.N C 1/ dimensional extended state vector as
y .t/ D Œx .t / ; x .t
1
/;x .t
2
/;:::;x .t
N
/
T
Œy
1
.t/ ; y
2
.t/ ; y
3
.t/;:::;y
N C1
.t/
T
: (12.17)
We obtain an equation for the vector y .t/ 2 R
M
.
P
y .t/ D
2
6
6
6
6
6
6
4
f
y
1
.t/ ; y
N C1
.t/ ; t
1
Œy
1
.t/ y
2
.t/
:
:
:
1
Œy
N
.t/ y
N C1
.t/
3
7
7
7
7
7
7
5
C
2
6
6
6
4
B
0
:
:
:
0
3
7
7
7
5
u .t/
O
f.y;t/C
O
Bu .t/ : (12.18)
For a linear system
P
x D Ax .t/ CA
x .t /CBu .t/ ; (12.19)
where A is the R
nn
state matrix and A
is the R
nn
state matrix related to the
delayed response, we have an equation for y .t/ 2 R
M
as
P
y .t/ D
2
6
6
6
6
6
6
6
6
6
4
A0 0A
1
I
1
I0 0
:
:
:
:
:
:
0 0
1
I
1
I
3
7
7
7
7
7
7
7
7
7
5
y .t/ C
2
6
6
6
4
B
0
:
:
:
0
3
7
7
7
5
u .t/
O
Ay .t/ C
O
Bu .t/ ; (12.20)

140 B. Song and J.-Q. Sun
where
O
A 2 R
M M
and
O
B 2 R
M m
. Recall that
i
need not to be spaced uniformly
in the time interval Œ0; . Nonuniform sampling allows the method to handle more
than one independent time delays [14].
12.3 Spectral Properties of the Methods
Both the methods of semi-discretization and CTA focus on approximationof tempo-
ral responses of the system over a short time interval. As N !1, the approximate
solution approaches the exact one in time domain at the rate depending on the order
of the local approximation. This has been verified by means of extensive numerical
simulations [12–14,31].
These methods are not specifically developed to meet frequency dominant re-
quirements such as accurate representation of the open-loop or closed-loop poles
and zeros of the original system. The methods have been mostly validated with
time domain numerical solutions. Their properties in frequency dominant are stud-
ied next with the help of numerical examples of a linear time-delayed system. Since
the CTA formulation can be made completely equivalent to semi-discretization for
linear time-invariant systems with a single time delay, the spectral properties of the
CTA method are the same as that of semi-discretization.
Consider a linear spring–mass–dashpot oscillator subject to a delayed PD con-
trol. The closed-loop characteristic equation is given by
s
2
C cs C k C k
p
e
s
C k
d
se
s
D 0; (12.21)
wherewetakec D 0:2, k D 4,and D =2. k
p
and ka
d
are the feedback gains.
The state matrix with the CTA method reads
O
A D
2
6
6
6
6
6
6
6
6
6
6
6
4
01
k c
00
k
p
k
d
1
I
1
I0 0
:
:
:
:
:
:
0 0
1
I
1
I
3
7
7
7
7
7
7
7
7
7
7
7
5
: (12.22)
From the stability chart in [13], we know that the system is stable when .k
p
;k
d
/ D
.0:5; 0:5/. There are two pairs of the dominant poles with real parts approxi-
mately equal to 1 and 0:4. Figures 12.1 and 12.2 show the roots of the char-
acteristic equation (12.21) and the eigenvalues of the state matrix (12.22) con-
structed with the forward central difference and fourth order Gear’s integration
algorithm [33]. Extensive simulations show that the CTA method is able to cap-
ture the dominant poles of the system only, and completely misses the fast and high
frequency poles.
12 Control of Systems with Time Delay 141
−40 −20 0
−50
0
50
ab
Re(s)
Im(s)
−20
−10
0
−20
−15
−10
−5
0
5
10
15
20
Re(s)
Im(s)
Fig. 12.1 Closed-loop poles of the linear oscillator under a delayed PD control. “” denotes
the roots of the characteristic equation (12.21). “C” denotes the eigen values of the state ma-
trix (12.22) constructed with forward finite difference approximation. .k
P
;k
D
/ D .0:5; 0:5/.
k D 4: c D 0:2. D =4. N D 20.(b) is the zoomed view of (a) in the indicated range
−100 −50 0
−50
0
50
Re(s)
Im(s)
−20 −10 0
−20
−15
−10
−5
0
5
10
15
20
Re(s)
Im(s)
ab
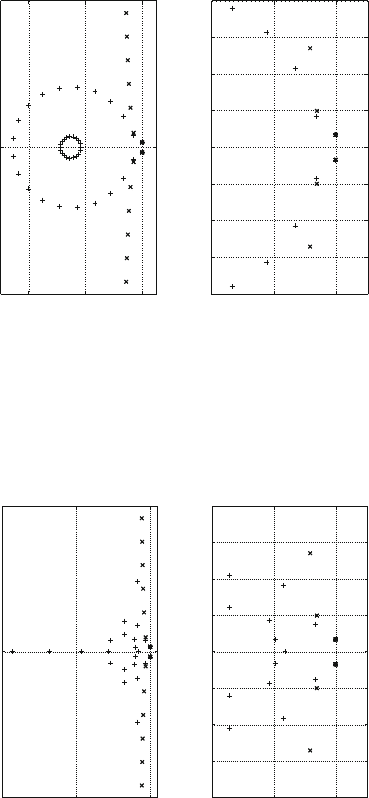
Fig. 12.2 Closed-loop poles of the linear oscillator under a delayed PD control. denotes the
roots of the characteristic equation (12.21). “C” denotes the eigen values of the state matrix (12.22)
constructed with the fourth order Gear’s integration scheme. .k
P
;k
D
/ D .0:5; 0:5/. k D 4.
c D 0:2. D =4. N D 20.(b) is the zoomed view of (a) in the indicated range
The central finite difference for CTA yields more accurate solutions in time
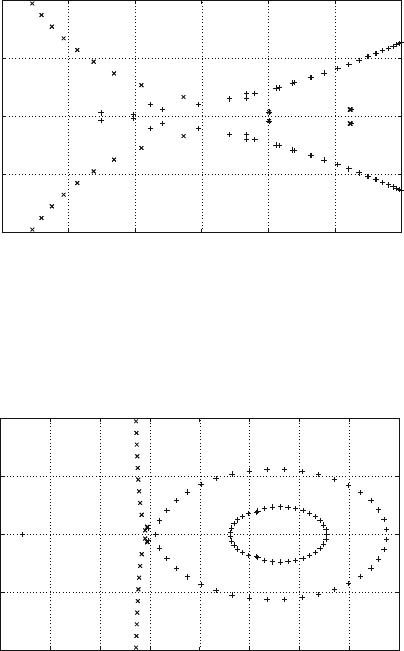
domain. But it introduces a set of lightly damped poles as shown in Fig. 12.3.This
causes difficulties when the method is used in control design. On the other hand,
the backward finite difference for CTA is unstable, even though it also accurately
142 B. Song and J.-Q. Sun
−3 −2.5 −2 −1.5 −1 −0.5 0
−40
−20
0
20
40
Im(s)
Re(s)
Fig. 12.3 Closed-loop poles of the linear system with central finite difference approximation
of the delayed portion of the response under a delayed PD control. “” denotes the roots of
the characteristic equation (12.21). “C” denotes the eigen values of the state matrix (12.22).
.k
P
;k
D
/ D .0:5; 0:5/. k D 4. c D 0:2. D =2. N D 40
−30 −20 −10 0 10 20 30 40 50
−40
−20
0
20
40
Re(s)
Im(s)
Fig. 12.4 Closed-loop poles of the linear system with backward finite difference approxima-
tion of the delayed portion of the response under a delayed PD control. “” denotes the roots
of the characteristic equation (12.21). “C” denotes the eigen values of the state matrix (12.22).
.k
P
;k
D
/ D .0:5; 0:5/. k D 4. c D 0:2. D =2. N D 40
captures the dominant poles as shown in Fig. 12.4. Furthermore, all the methods can
capture the right most dominant poles when the system is unstable. The results are
not presented here for the sake of space.
Why can the CTA method accurately predict temporal response x .t / of the time-
delayed system even when it misses all the fast and high frequency poles?
Recall that the response of time-delayed systems lives in an infinite dimen-
sional state space. x .t/ is a projection of the infinite dimensional response
.x .t/ ; x .t t
1
/;0 < t
1
/ on to the finite dimensional space R
n
. However,
different objects in a higher dimensional space can have the same projection in a
lower dimensional space. The CTA method aims at accurate time domain solutions

12 Control of Systems with Time Delay 143
of x .t/ for all t>0, much like the numerical algorithms for integrating ordinary
differential equations, such as Runge–Kutta methods whose frequency domain
properties are also rarely discussed. These methods in time domain provide one
projection of the infinite dimensional response, while the methods in frequency
domain such as Pad´e approximations of the transfer function provide a different
projection [34, 35]. In principle, the solutions x .t / obtained by both the time and
frequency domain methods with “equivalent accuracy” should be very close to each
other, while the solutions obtained by the frequency domain methods may have an
advantage of containing more accurate information about the poles and zeros.
The question is then, can we construct a time domain method that accurately
predicts both the temporal responses and the poles of the system?
12.4 Control Formulations
12.4.1 Full-State Feedback Optimal Control
Within the framework of continuous time approximation, we can formulate a full-
state feedback optimal control problem. Define a performance index as
J D
1
2
1
Z
0
y
T
Qy C u
T
Ru
dt; (12.23)
where Q D Q
T
0 and R D R
T
>0. When the linear system (12.20) is consid-
ered, the full state feedback control u DKy is the LQR control determined by the
matrices .
O
A;
O
B; Q; R/ [36]. When the nonlinear system (12.18) is considered, we
have a nonlinear optimal control problem on hand [37].
Note that the extended state vector y contains the current and past system re-
sponse x .t/. The full state feedback control does not consider possible transport
delays since the current state x .t/ is included in the control.
12.4.2 Output Feedback Optimal Control
Assume that there is a transport delay
p
. We consider a control of the form
u DKx.t
p
/ for the linear system. First, we select a discretization scheme
such that
p
is one of the points
i
of the time discretization. Assume that
p
D
k
.
Define an output equation as
v D Cy D y
kC1
D x.t
p
/; (12.24)
where y
kC1
is the .k C 1/th elemental vector defined in (12.17).
According to [36], if a control gain K for the linear system in (12.20) can be
found such that the closed-loop system characterized by the matrix
O
A
O
BKC

144 B. Song and J.-Q. Sun
is stable, the system is output stabilizable. When the system is output stabilizable,
an optimal control gain can be found in the following optimization problem: Find a
control gain K such that the performance index
J D
1
2
y
T
0
Py
0
D
1
2
tr
h
Py
0
y
T
0
i
; (12.25)
is minimized where y
0
is an initial condition of the extended state vector y.t/,
subject to the constraint of the Lyapunov equation
.
O
A
O
BKC/
T
P CP.
O
A
O
BKC/ C C
T
K
T
RKC C Q D 0: (12.26)
This is a nonlinear matrix algebraic optimization problem. The Matlab function
fminsearch can be used to find the optimal control. The optimal gain is in general
a function of the initial condition y
0
. This is not a desirable feature of the output
feedback control. A common approach to select initial conditions is to replace the
term y
0
y
T
0
by its statistical average EŒy
0
y
T
0
, i.e., the autocorrelation function of y
0
.
For more discussions, the reader is referred to [36].
It should be noted that for a given initial value of the control gain to start
searching for the optimal one, even the best searching algorithm only gives a lo-
cal minimum of the performance index J . There are many research issues with
the output feedback design that need further studies. For example, how to help the
searching algorithm land on a much deeper local minimum? How to select the de-
sign matrices Q and R to improve the control performance under certain constraints?
In the current formulation, when is the system output stabilizable? These turn out to
be tough technical questions to answer.
12.4.3 Optimal Feedback Gains via Mapping
Another way to obtain optimal gains for output feedback controls is via mapping.
This approach has been studied extensively in [12,13] with semi-discretization.
For the linear system (12.20), a mapping of the response can be constructed as
y.k C 1/ D ˆ.K/y.k/; k D 0; 1; : : : (12.27)
where u DKx.t
p
/ has been substituted. The mapping ˆ is therefore a function
of the control gain K. This mapping can be found either by the method of semi-
discretization or directly from the solution of Equation (12.20)givenby
y .t/ D e
O
At
y
0
C
t
Z
0
e
O
A.tt
1
/
O
Bu .t
1
/ dt
1
: (12.28)
We have found that the mapping constructed via CTA is completely equivalent to the
mapping via semi-discretization. When the system (12.20) is periodic with multiple
12 Control of Systems with Time Delay 145
independent time delays, we can combine the method of semi-discretization with
CTA to construct the mapping for the response of the system [31, 32].
Consider a bounded and compact region R
mn
such that K 2 . We can
find the domains of stability and optimal control gains in the region to minimize the
largest magnitude of the eigenvalues of ˆ. This leads to the following optimization
problem
min
K2
Œmax
j
.ˆ/
j
subject to jj
max
<1: (12.29)
This formulation offers a different approach to the design of output feedback con-
trols for linear periodic systems with or without time delay. The control performance
criterion is the decay rate of the mapping ˆ over one mapping step. In the frequency
domain, we have found that the optimal feedback gains designed by the mapping
method maximize the damping of the dominant closed-loop poles of the system that
are closest to the imaginary axis of the s-plane [13].
12.5 Supervisory Control
Recall the system in (12.30). The time delay is assumed to be slowly time-varying,
and lie in an interval Œ
min
;
max
, where the minimum and maximum time delays are
assumed to be known. Assume that we have obtained a set of optimal feedback
gains for the set of time delays sampled in the interval Œ
min
;
max
.Wepresentthe
switching algorithm for selecting a gain to implement in real time.
The actual time delay is such that
min
max
. We discretize Œ
min
;
max
into M
1 intervals, so that
min
D
1
<
2
<
M
D
max
. Consider M
models of the time-delayed system as
P
x
i
D f .x
i
.t/ ; x
i
.t
i
/;t/CBu
i
.t/ ; 1 i M
: (12.30)
Consider the feedback control u
i
DK
i
x
i
.t
i
/ where K
i
2 . Each K
i
is
found by imposing (12.29) subject to an additional constraint: K
i
must be stable for
all
j
(1 j M
). Let K
iOpt
2 be the optimal gain for
i
and the associate
eigenvalue with the smallest magnitude j
i
.ˆ/j
min
<1. Check if K
iOpt
stabilizes
the system in (12.30) for all other time delays
j
(1 j M
).
Following the concept of the supervisory control [27–30], we define an estima-
tion error as
e
i
D x
i
.t/ x .t/ ; 1 i M
; (12.31)
where x .t/ is the output of the system with unknown time delay. In the experiment,
x .t/ would be obtained from measurements. Consider a positive function of the
estimation error F
i
.e
i
/>0. An example is F
i
.e
i
/ Djje
i
jj
2
. Define a switching
index
i
.t/ such that
P
i
.t/ C
i
i
.t/ D F
i
.e
i
/; .
i
>0/
i
.0/ D 0; (12.32)

146 B. Song and J.-Q. Sun
where the parameter
i
defines the bandwidth of the low pass filter. The general
solution for
i
.t/ can be obtained as
i
.t/ D e
i
t
i
.0/ C
t
Z
0
e
i
.t/
F
i
.e
i
.//d: (12.33)
The hysteretic switching algorithm in [29, 30] is stated as follows. Assume that
the system is sampled at time interval t.Atthekth time step, the system is
under control with the gain K
j
and the associated switching signal is
j
.k/.At
the .k C 1/th step, if there is an index i such that
i
.k/ < .1 /
j
.k/ where
>0is a small number, we switch to the gain K
i
. Otherwise, we continue with
the gain K
j
. is known as the hysteretic parameter and prevents the system from
switching too frequently.
12.6 Numerical Examples
12.6.1 Linear Time Invariant System
Consider a second-order autonomous system under a delayed PI control.
P
x.t/ D
2
4
01 0
00 1
0 k c
3
5
x.t/
2
4
000
000
k
i
k
p
0
3
5
x.t /; (12.34)
where x D .x; Px; Rx/
T
. The feedback control u DŒk
i
;k
p
;0x.t / has an uncer-
tain transport delay
Take k D 4, c D 0:2. The discretization number of the time delayed response
is set to be N D 20 for all sampled time delays [12–14].
min
D 0:0419 and
max
D 0:2094. We pick five different time delays to design optimal feedback gains
according to the method outlined in the previous section.
The optimal gains associated with the five time delays are listed in Table 12.1.
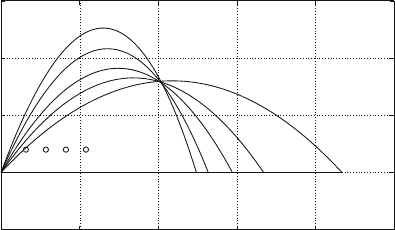
The associated stability domains in the gain space are shown in Fig. 12.5. It should
Table 12.1 Optimal PI feedback gains and jj
max
for the four sampled time delays of the linear time
invariant system
Time delay k
i
k
p
jj
max
1
D 0:0419 0.2000 1:8400 0.9992
2
D 0:0733 0.2000 2:3500 0.9982
3
D 0:1047 0.2000 2:8600 0.9966
4
D 0:1571 0.2000 2:8600 0.9938
5
D 0:2094 0.2000 3:3700 0.9907
12 Control of Systems with Time Delay 147
−4 −2 0 2 4 6
−0.5
0
0.5
1
1.5
k
p
k
i
Fig. 12.5 Stability domains (lines) in the gain space and the optimal feedback gains (o) for the
autonomous systems with four different time delays
i
(i D 1; 2; 3; 4; 5). The stability boundaries
become taller and narrower, and move upward along k
i
axis as time delay increases
be pointed out that when the optimal gains of all the controls with different time
delays fall in the intersection of the stability domains, it is possible to use the hys-
teretic algorithm to switch among the predesigned controls and to keep the system
stable all the time. When an optimal gain is out of the intersection, the control with
that gain can destabilize the system with some time delay in the range Œ
min
;
max
.
This property limits the size of the unknown time delay range Œ
min
;
max
because
the stability domains change significantly with the time delay, particularly for peri-
odic systems [13].
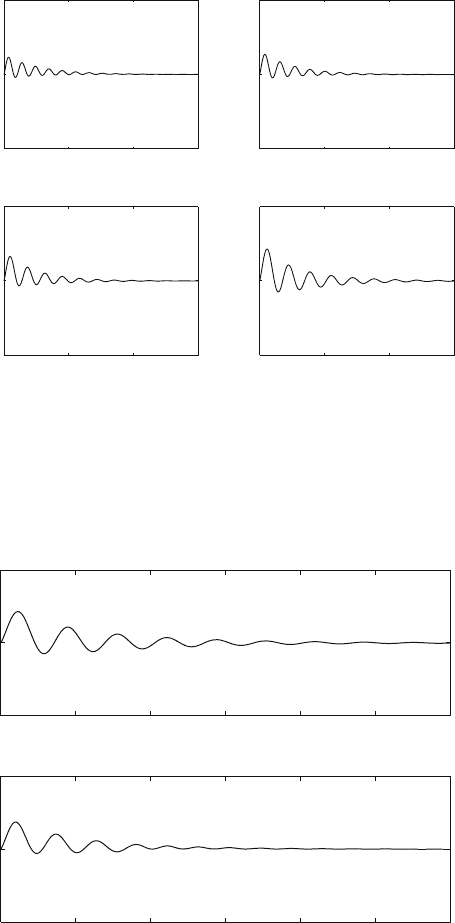
Figure 12.6 shows the closed loop response of the system under the feedback
control with all four different time delays when the system true time delay is taken
to be
4
and is assumed to be unknown. As it can be seen from the figure, when
the control designed for the time delay that is close to
4
is implemented, the per-
formance is acceptable. Otherwise, the performance can deteriorate as seen in the
left-upper sub-figure.
Next, we examine how well the hysteretic switch algorithm works. Assume that
we start with a control gain K
1
designed for
1
, while the system delay is
4
.
Figure 12.7 shows that the hysteretic algorithm is able to switch the control to K
3
and K
4
since both controls have a similar performance. Figure 12.8 shows the switch
signal .t/ and the control index.
12.6.2 Periodic System
Consider the Mathieu equation with a delayed PID feedback control
P
x.t/ D
2
4
010
001
4" sin 2t .ı C 2" cos 2t/ 0
3
5
x.t/
2
4
000
000
k
i
k
p
k
d
3
5
x.t /;
(12.35)
148 B. Song and J.-Q. Sun
0 20 40 60
−5
0
5
Time (s)
0 20 40 60
−5
0
5
0 20 40 60
−5
0
5
0 20 40 60
−5
0
5
Time (s)
τ
=
τ
1
, K=K
1
τ
=
τ
1
, K=K
3
, K
3
τ
=
τ
1
, K=K
5
τ
=
τ
1
, K=K
2
x
1
x
1
Fig. 12.6 Response of the autonomous system under feedback controls designed for a specific gain
when the system true time delay is
1
and is assumed to be unknown. When the feedback gains
.K
2
;K
3
;K
5
) are designed for the time delay close to the actual one, the control performance is
quite good. K
4
and K
5
are the same. When the mismatch gap is large, i.e. when K
5
designed for
5
is implemented for the system with time delay
1
, the performance deteriorates
0 10 20 30 40 50 60
−5
0
5
Time (s)
x
1
x
1
τ
=
τ
1
, K=K
5
0 10 20 30 40 50 60
−5
0
5
Time (s)
τ
=
τ
1
, Switch from K
5
Fig. 12.7 The closed loop response of the system under the switched control when the initial gain
of the control is K
5
designed for
5
while the system true time delay is
1
(bottom), as compared
to the case when the gain is fixed at K
5
(top)
