Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay
Подождите немного. Документ загружается.

14 On the Feedback Controlling of the Neuronal System with Time Delay 171
where x is the membrane potential of neuron, y is a recovery variable associated
with the fast current for a sodium current or a potassium current, and z is a slowly
changing adaptation current for a calcium current [14]. The model used the follow-
ing parameters: a D 1:0; b D 3:0; c D 1:0; d D 5:0; D1:6; r D 0:013;
s D 4:0; I D 3:1. The first equation of model (14.1) describes the effect of feed-
back connection. x.t / is the membrane potential at the earlier time t ,here
" is the synaptic intensity and is the time delay.
14.3 Influence of Synaptic Intensity " on the Neuronal
Discharge
The dynamic variation of neuronal discharge depending on the synaptic intensity
" are first studied in the absence of external stimulus with a fixed time-delay self-
feedback input, here D 14 ms.
It is seen from Fig. 14.1 that there is no firing for a smaller " and the mem-
brane potential exhibits only subthreshold oscillations. When synaptic intensity "
0 50 100 150 200 250 300
a
21.5 2.5 3 3.5
0 50 100 150 200 250 300
1.5 2 2.5 3 3.5
0 50 100 150 200 250 300
x / mv
1.5 2 2.5 3 3.5
x (t)
0 50 100 150 200 250 300
1.5 2 2.5 3 3.5
0 50 100 150 200 250 300
t / ms
1.5 2 2.5 3 3.5
z (t)
e
=
1.5ms
−
1
e
=
1.8ms
−
1
e
=
2.5ms
−
1
e
= 3.
1ms
−
1
e
=
4.6ms
−
1
−2
0
2
−2
0
2
−2
0
2
−2
0
2
−2
0
2
−2
0
2
−2
0
2
−2
0
2
−2
0
2
−2
0
2
b
c
d
e
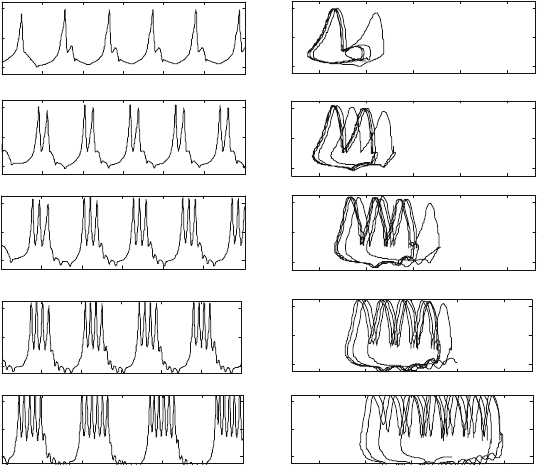
Fig. 14.1 Influence of synaptic intensity " on the neuronal firing behavior when D 14 ms,
with increasing the synaptic intensity ", the neuron exhibits different discharge patterns, such as:
period-1 for " D 1:5 ms
1
(a), period-2 for " D 1:8 ms
1
(b), period-3 for " D 2:5 ms
1
(c),
period-4 for " D 3:1 ms
1
(d), period-5 for " D 4:6ms
1
(e); the right part shows the phase
space of x z
172 H. Liu et al.
increases greater than the threshold "
th
, for different synaptic strength, the neuron
displays different discharge patterns (shown in the left of Fig. 14.1) and phase space
(shown in the right of Fig. 14.1), transforming among resting, tonic, and bursting
state. For fixed D 14 ms, with synaptic intensity " changing from 1.5 to 4:6 ms
1
,
the neuronal spike changes from period-1 to period-5 as shown in Fig. 14.1a–e,
respectively; sometimes, the period-2, period-3, period-4, etc. are generally called
bursting spike. We also found out that the neuron firing behavior disappears and the
membrane potential keeps at a constant value for too bigger synaptic intensity of ",
(e.g., " 15 ms
1
).
14.4 Influence of Time Delay £ on the Neuronal Discharge
Next, the time delay is the other one important factor in neuroinformation transfer-
ring and disposal for neural system, so the influence depending on time delay of
feedback control can also be investigated in this section, the synaptic intensity is
fixed at 3:18 ms
1
.
The neuron displays rest state when the delay time smaller than 5 ms, as shown
in Fig. 14.2a. When rises up to 5 ms gradually, the neuron exhibits likewise dif-
ferent discharge patterns (shown in the left of Fig. 14.2) and phase space (shown in
the right of Fig. 14.2), as well as realizing the transition from testing, spiking, burst-
ing state. For fixed " D 3:18 ms
1
, with time delay changing from 5 to 14 ms,
the neuronal firing changes from period-1 to period-4 as shown in Fig. 14.2b–e,
respectively.
With positive feedback with time delay, both " and could affect the firing pat-
terns of the HR neuron in the absence of the stimulus current, along with increasing
of the synaptic intensity or time delay, the neuron will change from periodic spike
to burst spike actives.
14.5 Controlling Chaotic Discharge by Feedback Control
with Time Delay
The controlling of chaotic discharges of the HR model neuron is investigated in this
work. One external stimulus current is introduced to the first equation of neuron
model [shown in (14.1)] to generate chaotic discharges in the absence of time-delay
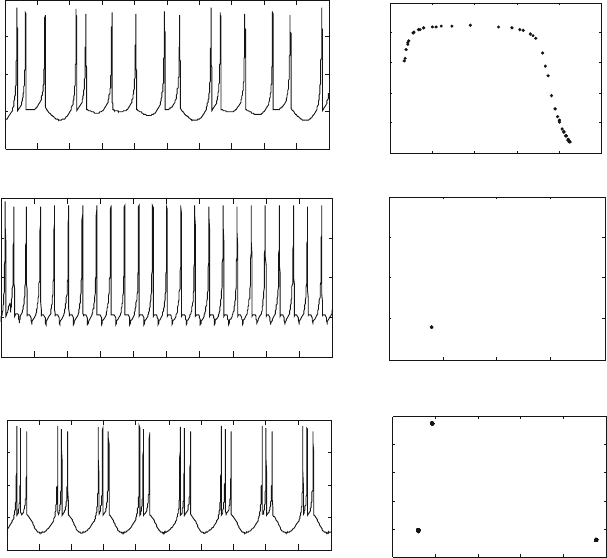
part; here, the external stimulus is set as 3:12 A. The neuronal discharge represents
chaotic firing, as shown in Fig. 14.3a, and its chaotic characteristics, chaotic saddle,
could be easily found in the return map of ISI (interspike interval) as shown in
Fig. 14.3b. Then the feedback control with time delay is added to the model too;
the results suggested that the neuronal chaotic discharges could be controlled to
tonic firing, as two examples, when the synaptic strength " D 1:8 ms
1
and time
14 On the Feedback Controlling of the Neuronal System with Time Delay 173
0 50 100 150 200 250 300
−2
0
2
1.5 2 2.5 3 3.5
0 50 100 150 200 250 300
−2
0
2
1.5 2 2.5 3 3.5
−2
0
2
0 50 100 150 200 250 300
−2
0
2
x / mv
1.5 2 2.5 3 3.5
x (t)
0 50 100 150 200 250 300
−2
0
2
1.5 2 2.5 3 3.5
−2
0
2
0 50 100 150 200 250 300
−2
0
2
t / ms
1.5 2 2.5 3 3.5
z (t)
t =
3ms
t =
5ms
t =
8ms
t =
12ms
t =
14ms
−2
0
2
−2
0
2
−2
0
2
a
b
c
d
e
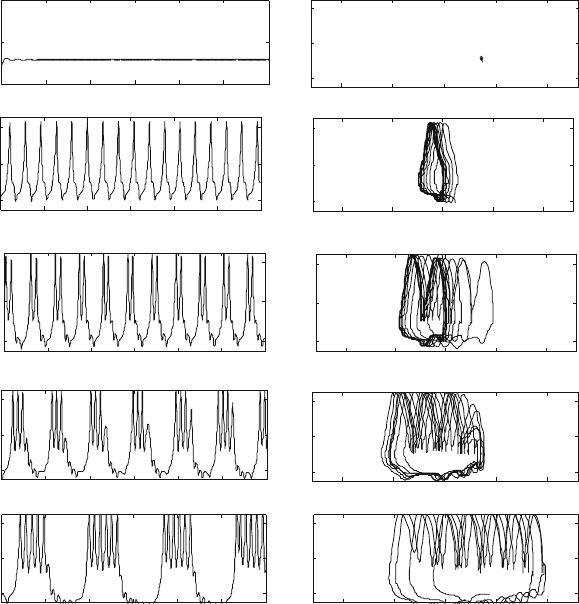
Fig. 14.2 Influence of time delay on the neuron firing behavior when " D 3:18 ms
1
, with
increasing the time delay , the neuron also exhibits different discharge patterns, such as: rest-
firing for D 3 ms (a), period-1 for D 5 ms (b), period-2 for D 8 ms (c), period-3 for
D 12 ms (d), period-4 for D 14 ms (e); the right part shows the phase space of x z
delay D 6 ms, the chaotic discharges are replaced by period-1 discharges (see
Fig. 14.3c, d), and when " D 1:76 ms
1
and D 12 ms the neuron displays period-
3 activities (see Fig. 14.3e, f).
14.6 Conclusions
The firing responses of an individual HR model neuron with time delay by synapse
have performed numerical investigations in this work; for the different feedback
inputs, the neuron shows rich and complex dynamical firing activities. The scal-
ing of synaptic intensity " and time delay could trigger many kinds of periodic
174 H. Liu et al.
0 20 40 60 80 100
0
20
40
60
80
100
ISI ( n )
ISI (n+1)
10 20 30 40 50
10
20
30
40
50
ISI(n)
10 20 30 40 50 60
10
20
30
40
50
60
ISI ( n )
ISI (n+1)
0 50 100 150 200 250 300 350 400 450 500
t / ms
x / mv
0 50 100 150 200 250 300 350 400 450 500
t / ms
x / mv
0 50 100 150 200 250 300 350 400 450 500
t / ms
x / mv
−2
−1
0
1
2
ab
c d
ef
−2
−1
0
1
2
−2
−1
0
1
2
ISI(n+1)
Fig. 14.3 With parameter r D 0:015 and the external stimulus current 3:12 A, the HR neuron
shows chaotic discharges for " D 0 ms
1
(a, b); period-1 firing for " D 1:8 ms
1
and D 6 ms
(c, d); period-3 firing for " D 1:76 ms
1
and D 12 ms (e, f), respectively
oscillation in the absence of the stimulus current, and the neuronal chaotic discharge
could also be controlled to period-1 or period-3 discharge by feedback control with
time delay.
Acknowledgments We are grateful for the support of the National Natural Science Foundation of
China under Grant Nos. 30670529 and 10572056.
References
1. Just W, Bernard T, Ostheimer M, Reibold E, Benner H (1997) Mechanism of time-delayed
feedback control. Phys Rev Lett 78(2):203–206
2. Hu HY, Wang ZH (1998) Stability analysis of damped SDOF systems with two time delays in
state feedback. J Sound Vib 214:213–225
14 On the Feedback Controlling of the Neuronal System with Time Delay 175
3. Ji CJ, Leung AYT (2002) Resonances of a non-linear sdof system with two time-delays in
linear feedback control. J Sound Vib 253(5):985–1000
4. Sainz-Trap´aga M Masoller C, Braun HA Huber MT (2004) Influence of time-delayed feedback
in the firing pattern of thermally sensitive neurons. Phys Rev E 70:1–11
5. Yu HJ, Peng JH (2005) Chaotic control of the Hindmarsh–Rose neuron model. Acta Biophysica
Sin 21(4):295–300
6. Ott E, Grebogi C Yorke JA (1990) Controlling chaos. Phys Rev Lett 64(11):1196–1199
7. Sinha H (1991) An efficient control algorithm for nonlinear systems. Phys Lett A 156:475–478
8. Huberman BA Lumer EL (1990) Dynamics of adaptive system. IEEE Trans on CAS
37(4):547–550
9. Pyragas K (1993) Experimental control of chaos by delayed self controlling feedback. Phys
Lett A 180:99–102
10. Pyragas K (1992) Continuous control of chaos by self-controlling feedback. Phys Lett A
170:421
11. Diez-Martines O, Segundo JP (1983) Behavior of a single neuron in a recurrent excitatory loop.
Biol Cybern 47:33–41
12. Gong YF, Xu JX, Ren W, Hu SJ, Wang FZ (1996) Bifurcation, chaos and control in nervous
system, Acta Biophys Sin 12:663
13. Zheng YH, Lu QS (2008) Synchronization in ring coupled chaotic neurons with time delay.
J Dyn Control 06(3):208–212
14. Hindmarsh JL, Rose RM (1984) A model of the nerve impulse using two first-order differential
equations Nature 296:162

Chapter 15
Control of Erosion of Safe Basins in a Single
Degree of Freedom Yaw System of a Ship
with a Delayed Position Feedback
Huilin Shang
Abstract A single degree of freedom nonlinear yaw system of a ship with autopilot
force and wave exciting force is investigated in this chapter. The delayed position
feedbacks are applied to control erosion of safe basins in the dynamical system for
increasing the ship’s safe possibility. Considering time delay as a variable parameter
and employing the fourth Runge–Kutta and Monte Carlo methods, the evolutions of
boundary and area of safe basins with time delay are presented. For a short delay,
the mechanism of the evolution of safe basin is studied analytically. It is found that
the delayed position feedback can be used as a good strategy to control the erosion
of safe basins of the rolling motion system.
15.1 Introduction
It is well known that the unacceptably large motions in engineering dynamical
system under consideration may lead to the failure of the system [1–5]. For example,
ship at sea may capsize under wave excitation when the roll-motion angle of the ship
is too large [2–4]. The safe basin is induced to study the phenomena which is the
union of basins of attraction of all bounded solutions for a system [2,3]. The erosion
of safe basins due to the penetration of tongues from the “dangerous” attractors is
an unwanted and dangerous phenomenon from a practical point of view. Therefore,
it is necessary to investigate the basin erosion and its possible control. The control
methods, which are used to enlighten the loss of safety of the structure, have been
devoted much attention during decades [6–10]. Various integrity measures, such as
GIM [6], LIM [6], and IF [7], are applied to study the evolution of the system. Varia-
tion of a system parameter may induce or control the basin erosion globally [8–10].
It is found that the erosion of safe basins can be aggravated by the Gaussian white
H. Shang (
)
School of Mechanical and Automation Engineering, Shanghai Institute of Technology,
Shanghai 20035, People’s Republic of China
e-mail: suliner60@hotmail.com
A.C.J. Luo (ed.), Dynamical Systems: Discontinuity, Stochasticity and Time-Delay,
DOI 10.1007/978-1-4419-5754-2
15,
c
Springer Science+Business Media, LLC 2010
177
178 H. Shang
or bounded noise excitation [8] but be controlled by the increasing of the damping
[9,10] or the decreasing of the excitation amplitude [11].
In this chapter, we aim to control the erosion of safe basins in nonlinear systems
by the delayed position feedbacks. Many obtained results [12–14] shows that ap-
plying a delayed feedback in a dynamical system also may be a good approach
to control dynamical motions of the system. We study a nonlinear yaw system of
a ship, where the autopilot force acted on and the wave exciting force are taken
into account
Rx C c Px C x x
3
D G cos t; (15.1)
which is a softening Duffing oscillator and x in (15.1) represents the roll-motion
angle of the ship. By adding the delayed position feedback to the system, one may
obtain that
Px D y;
Py Dcy x C x
3
C G cos t C A.x.t / x/; (15.2)
where is time delay and A the feedback gain. When D 0, the system (15.2) can
be reduced to the system (15.1).
For a system modeled by an ordinary differential equation (ODE), the safe basin
is defined [2]. However, it is difficult to describe and study the safe basin for DDE,
since initial conditions are completely different from those for ODE. Solutions of
DDE are determined by initial conditions z.t/ D z
0
for t D 0 and z.t/ D .t/
for t<0. Thus, regions of attraction of various solutions are located
within a polyhedron composed of the initial phase space with the thickness .It
is unintuitively to observe dynamical behaviors on such regions of attraction. How-
ever, the regions of attraction can be projected to the initial phase space given by
z.0/ Dfz
1
.0/; z
2
.0/; : : : ; z
n
.0/g
T
for controlled systems with delayed feedbacks,
since there is not any signal to be returned into systems before t D 0. Therefore,
the safe basin in (15.2) can be studied on the plane where the x-axis is x.0/ and the
y-axis y.0/.
In this chapter, the effect of the delay or the feedback gain on the erosion of safe
basins is discussed in some detail in system (15.2). Section 15.2 presents variations
of boundaries of safe basins numerically when one changes the delay in the delayed
position feedback. In Sect. 15.3, the variation of the basin area with the delay is
displayed and the mechanism of the variation is explained when the delay is short.
In Sect. 15.4, results are summarized and discussed.
15.2 Effects of the Time Delay on the Basin Boundary
To determine boundaries of the solutions of the system (15.2), we generate figures
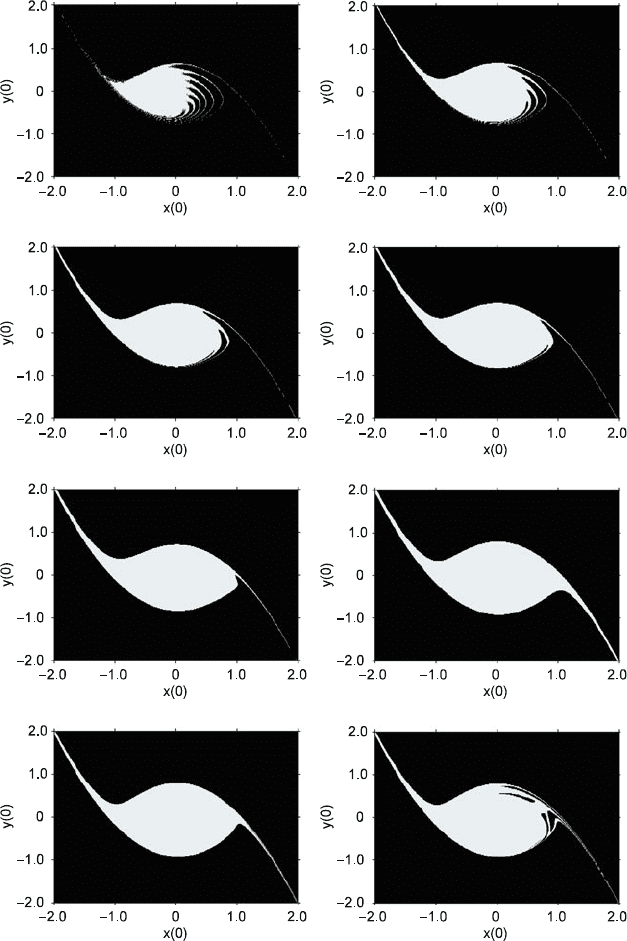
of safe basins when ˝ D 1:0; c D 0:01; A D 0:2,and increases from 0 to
7=5 asshowninFigs.15.1 and 15.2 for G D 0:1 and G D 0:3, respectively.
The region of attraction is drawn in the sufficiently large space region defined as
15 Control of Safe Basin by Delayed Feedbacks 179
ab
cd
ef
gh
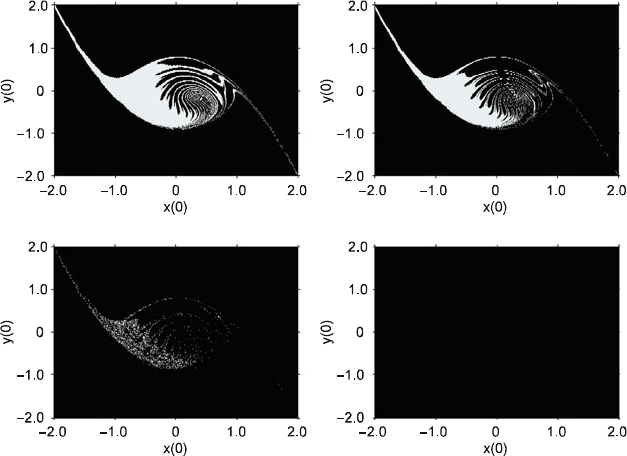
Fig. 15.1 Evolution of the safe basin as increases for G D 0:1 where (a) D 0,(b) D =50,
(c) D =25,(d) D 3=50,(e) D 2=25,(f) D 4=5,(g) D ,(h) D 26=25
180 H. Shang
ij
kl
Fig. 15.1 (continued) (i) D 27=25,(j) D 29=25,(k) D 31=25,and(l) D 7=5
2 x.0/ 2; 2 y.0/ 2 by generating a 640 240 array of starting
conditions for each of those starting points. The escaping set for infinite time is
approximated with good accuracy by a study with 10,000 excited circles. The time
step is taken as 1/4,000 of the period of excitation. The white and black regions are
numerical approximationsto the safe basin and the basins of attraction of unbounded
solutions, respectively.
When G ¤ 0, the system (15.2) is a nonautonomous system. It is well known
that the boundary of the safe basin in a nonautonomous system may be fractal and
have a noninteger dimension without time delay [10, 11]. Figure 15.1 presents a se-
quence of safe basins for (15.2)whenG D 0:1 and the delay varies. For D 0,
the safe basin is fractal as shown in Fig. 15.1a. With increasing from 0 to 4=5
(see Figs. 15.1a–e), the safe basin is enlarged, and its boundary becomes smoother
and smoother. When grows to 2=25 (see Fig. 15.1e), the fractal dimension is
near 2.0. As the delay increases from 4=5 to (see Fig. 15.1f, g), the safe basin
becomes small but its boundary is still completely smooth. Then a small increase
for the value of the delay makes the fingers of the basin return back to the boundary
(see Fig. 15.1h). Figure 15.1h–l shows the evolution of the basin by fractal with
increasing. When D 27=25, fingers from fractal suddenly begin to erode the in-
ner region of the safe basin, which leads to the strong erosion as shown in Fig. 15.1i.
As the delay continues to grow, the fractal structure also becomes more and more
visible. It follows from Fig. 15.1h–l that such evolution of the erosion in the inner
15 Control of Safe Basin by Delayed Feedbacks 181
ab
cd
ef
gh
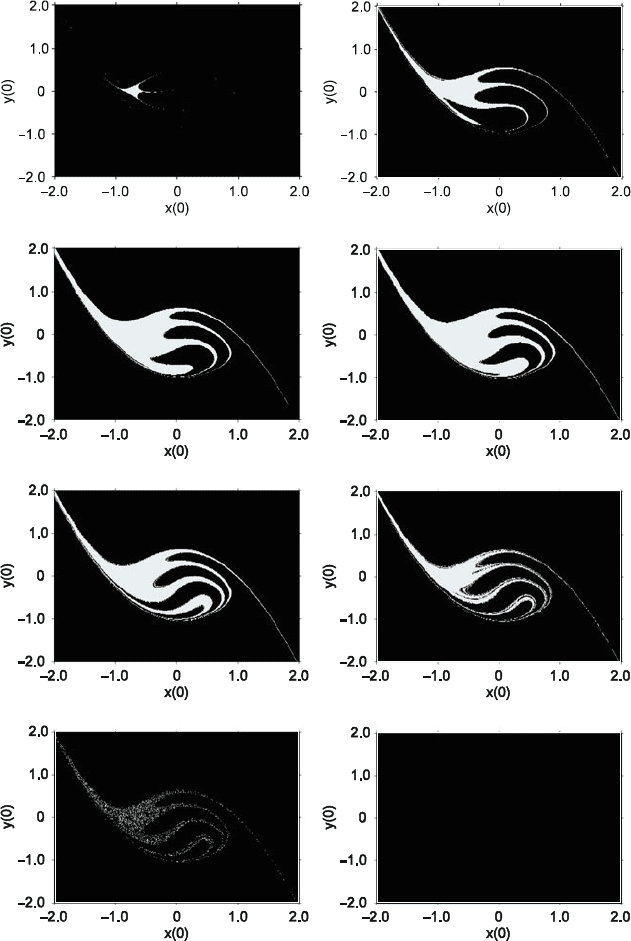
Fig. 15.2 Evolution of the safe basin as increases for G D 0:3 where (a) D 0,(b) D =5,
(c) D 2=5,(d) D 13=25,(e) D 16=25,(f) D 73=100,(g) D 37=50,and
(h) D 7=5
