Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay
Подождите немного. Документ загружается.

17 Impulsive Control Induced Effects on Dynamics of Complex Networks 205
functions of above complex networks will be discussed. The first part is the stability
analysis of the presented dynamical networks with different dynamical nodes with
impulsive control.
17.2.1 Stability Analysis of the Presented Dynamical Networks
with Different Dynamical Nodes with Impulsive Control
Consider the impulsive control of complex networks (17.1) with different dynamics
of each node. That is, f
i
¤ f
j
;.i ¤ j; i; j D 1;2;:::;N/. It can be described by
8
ˆ
ˆ
ˆ
<
ˆ
ˆ
ˆ
:
Px
i
D f
i
.x
i
/ C
N
P
j D1;:::;N
b
ij
x
j
;t¤ t
k
;
x
i
.t/ D I
k
.x
i
.t//; t D t
k
;
x
i
t
C
0
D x
i0
;kD 0;1;:::; i D 1;2;:::;N;
(17.2)
where f
i
.x
i
/WD!R
n
;t
1
>t
0
and impulse function I
k
.x
i
/ W D!R
n
;kD0; 1; 2; : : :.
Impulsive instants ft
k
g
1
kD0
!1;t
1
<t
2
< <t
k
< ; lim
k!1
t
k
D1,andsup
k
ft
kC1
t
k
g<ıIx
i
j
tDt
k
Dx
i
t
C
k
x
i
.t
k
/DI
k
.t; x
i
/; where x
i
t
C
k
D lim
t!t
C
k
x
i
.t/; x
i
.t
k
/
D lim
t!t
k
x.t/Dx
i
t
k
.
Few studies were focused on complex networks with different dynamical nodes
by impulsive control for existing results. And in this chapter, the impulsive func-
tion is different from existing results. Choose I
k
.x
i
/ D z
k
B
k
C C
k
x
i
x
i
, C
k
is an n n constant matrix, B
k
is a column vector, and z
k
is a discrete model
outer input state variable, such as from the Logistic model etc. Denote x
i
D
.x
i1
;x
i2
;:::;x
in
/
T
;i D 1;2;:::;N;XD
x
T
1
;x
T
2
; ;x
T
N
T
;f
i
.x
i
/DA
i
x
i
C
'
i
.x
i
/; A
i
2 R
nn
;
'
T
1
.x
1
/;'
T
2
.x
2
/;:::;'
T
N
.x
N
/
T
DF.X/;
A D
2
6
4
A
1
::: 0
:
:
:
:
:
:
:
:
:
0 ::: A
N
3
7
5
:
System (13.2) can be rewritten as
8
<
:
P
X D AX C F.X/C .B ˝ /X; t ¤ t
k
;
X D z
k
.I
N
˝ B
k
/ C .I
N
˝ C
k
/X .I
N
˝ I
n
/X; t D t
k
;
X.t
C
0
/ D X.t
0
/ D .x
T
1
.t
0
/; x
T
2
.t
0
/; ;x
T
N
.t
0
//
T
D X
0
;
(17.3)
where I
n
;I
N
are n n and N N unit matrix respectively.
We have the following theorem from results [25, 26].
Theorem 1. Suppose the series fz
k
g of impulsive differential equation (17.3) as
z
kC1
D z
k
.1 z
k
/ and the impulsive interval is , then the solution of system
(17.3) is changed with different value of in Logistic model. Especially, the trivial

206 X. Han and X. Fu
solution of system (17.3) is global asymptotical stable as 0< 1 for impulsive
B
k
;C
k
;k D 0; 1; 2; : : : That is the impulsive controlled networks in (17.2) is global
asymptotical stable at origin.
17.2.2 Impulsive Control Induced Effects on Dynamics
of Complex Networks with Identical Dynamical Nodes
Suppose that f
1
DDf
N
D f , complex networks (17.1) can be described by
Px
i
D f.x
i
/ C
N
X
j D1;:::;N
b
ij
x
j
D Ax
i
C '.x
i
/ C
N
X
j D1
b
ij
x
j
;iD 1;2;:::;N:
(17.4)
And suppose the following assumption holding.
Assumption 1. There exists a constant L>0such that all the nonlinear functions
k'.x
i
/ '.x
j
/kLkx
i
x
j
k for all i ¤ j.i;j D 1;2;:::;N/.
Definition 1. Complex networks (17.4) is called realize synchronization if
lim
t!1
kx
i
.t/ x
j
.t/kD0 for all i; j D 1;2;:::;N.
Consider the impulsive control of the presented model:
8
ˆ
ˆ
ˆ
ˆ
<
ˆ
ˆ
ˆ
ˆ
:
Px
i
D Ax
i
C '.x
i
/ C
N
P
j D1
b
ij
x
j
;t¤ t
k
;
x
i
.t/ D I
k
.x
i
.t//; t D t
k
;
x.t
C
0
/ D x
0
;kD 0;1;:::;
(17.5)
where I
k
.z
k
;x
i
/ D z
k
B
k
C C
k
x
i
x
i
, C
k
is an n n constant matrix, B
k
is a
column vector and z
k
is a discrete model outer input state variable, such as from the
Logistic model etc. Assume that s D
1
N
N
P
iD1
x
i
is the synchronization state of the
complex networks. Then, we have
8
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
<
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
:
Ps D
1
N
N
P
iD1
Px
i
D As C
1
N
N
P
iD1
'.x
i
/ DN'; t ¤ t
k
;
s D z
k
B
k
C C
k
s s; t D t
k
;
s
t
C
0
D
1
N
N
P
iD1
x
i
.t
0
/; t
0
>0:
(17.6)

17 Impulsive Control Induced Effects on Dynamics of Complex Networks 207
Let
e
i
D .e
i1
;e
i2
;:::;e
in
/
T
D x
i
s; i D 1;2;:::;N
, the dynamical error
equation is
Pe
i
D Ae
i
C
N
X
j D1
b
ij
x
j
C
1
N
N
X
iD1
.'.x
i
/ '.x
j
//; t ¤ t
k
;
e
i
D C
k
e
i
e
i
;tD t
k
;iD 1;2;:::;N: (17.7)
Definition 2. Complex network (17.4) is called realize synchronize if lim
t!1
kx
i
.t/
s.t/kD0 for all i D 1;2;:::;N. And the synchronization state is the orbit of s.
Denote
max
.X/ as the maximum eigenvalues of a square matrix X. Then, we have
Theorem 2. Let ˇ
k
D
max
C
T
k
C
k
;
1
D max
iD1;2;:::;N
.
max
..ACb
ii
/
T
C.AC
b
ii
///;
2
D
max
. /; b D max
iD1;:::;N
b
ii
:
(i) If D
1
C 2b
2
C 4L < 0 ( is a constant), and there exists a constant
˛.0 ˛</, such that lnˇ
k
˛.t
k
t
k1
/ 0; k D 1;2;:::, then the
impulsive control coupled system (17.5) realize synchronization.
(ii) If D
1
C2b
2
C4L 0 ( is a constant) and there exists a constant ˛ 1,
such that ln.˛ˇ
k
/ C .t
kC1
t
k
/ 0; k D 1;2;:::;then ˛ D 1 implies that
the trivial solution of the system (17.7) is stable and ˛>1implies the trivial
solution is globally asymptotically stable. That is, the impulsive control coupled
system (17.5) realize synchronize.
Proof. Construct a Lyapunov function V.e/ D
1
2
N
P
1
e
T
i
e
i
!
.Fort 2 .t
k1
;t
k
.k D 1;2;:::/, the time derivative of along the trajectory of system (17.7)is
P
V.e
1
;:::;e
N
/
D
1
2
N
X
iD1
Pe
T
i
e
i
C e
T
i
Pe
i
D
1
2
N
X
iD1
0
@
0
@
Ae
i
C
N
X
j D1
b
ij
e
j
C
1
N
N
X
j D1
.'.x
i
/ '.x
j
//
1
A
T
e
i
Ce
T
i
0
@
Ae
i
C
N
X
j D1
b
ij
e
j
C
1
N
N
X
j D1
.'.x
i
/ '.x
j
//
1
A
1
A
208 X. Han and X. Fu
D
1
2
N
X
iD1
0
@
e
T
i
..A C b
ii
/
T
C .A C b
ii
//e
i
C 2
N
X
j D1;j ¤i
e
T
i
b
ij
e
j
C2e
T
i
1
N
N
X
j D1
.'.x
i
/ '.x
j
//
1
A
1
2
N
X
iD1
max
..A C b
ii
/
T
C .A C b
ii
//e
T
i
e
i
C
N
X
iD1
N
X
j D1;j ¤i
e
T
i
b
ij
e
j
C
N
X
iD1
e
T
i
1
N
N
X
j D1
.'.x
i
/ '.x
j
//
1
2
N
X
iD1
max
..A C b
ii
/
T
C .A C b
ii
//e
T
i
e
i
C
N
X
iD1
N
X
j D1;j ¤i
b
ij
2
jje
T
i
jjjje
j
jj
C
1
N
N
X
iD1
N
X
j D1
jje
i
jjjj.'.x
i
/ '.x
j
//jj
1
2
N
X
iD1
max
..A C b
ii
/
T
C .A C b
ii
//e
T
i
e
i
C
N
X
iD1
N
X
j D1;j ¤i
b
ij
2
jje
T
i
jjjje
j
jj
C
L
N
N
X
iD1
N
X
j D1
jje
i
jjjjx
i
x
j
jj
1
1
2
N
X
iD1
e
T
i
e
i
!
C
N
X
iD1
N
X
j D1;j ¤i
2
b
ij
1
2
e
T
i
e
i
C e
T
j
e
j
C
L
N
N
X
iD1
N
X
j D1
jje
i
jj.jjx
i
sjj C jjs x
j
jj/
1
1
2
N
X
iD1
e
T
i
e
i
!
C
N
X
iD1
N
X
j D1;j ¤i
2
b
ij
1
2
e
T
i
e
i
Ce
T
j
e
j
C
L
N
N
X
iD1
N
X
j D1
.jje
i
jj
2
Cjje
i
jjjje
j
jj/
17 Impulsive Control Induced Effects on Dynamics of Complex Networks 209
1
1
2
N
X
iD1
e
T
i
e
i
!
C
2
2
N
X
iD1
0
@
b
ii
e
T
i
e
i
C
N
X
j D1;j ¤i
b
ij
e
T
j
e
j
1
A
C
L
N
N
X
iD1
0
@
0
@
N
X
j D1
jje
i
jj
2
1
A
C
1
2
N
X
j D1
e
T
i
e
i
C e
T
j
e
j
1
A
1
1
2
N
X
iD1
e
T
i
e
i
!
C
2
2
0
@
N
X
iD1
b
ii
e
T
i
e
i
C
N
X
iD1
0
@
N
X
j D1;j ¤i
b
ij
e
T
j
e
j
1
A
1
A
C
L
N
0
@
N
X
iD1
Ne
T
i
e
i
C
1
2
N
X
iD1
0
@
N
X
j D1
e
T
i
e
i
C e
T
j
e
j
1
A
1
A
1
1
2
N
X
iD1
e
T
i
e
i
!
C
2
2
0
@
N
X
iD1
b
ii
e
T
i
e
i
C
N
X
iD1
0
@
N
X
j D1;j ¤i
b
ij
e
T
j
e
j
1
A
1
A
C
L
N
N
X
iD1
2Ne
T
i
e
i
!
1
1
2
N
X
iD1
e
T
i
e
i
!
C
2
2
N
X
iD1
b
ii
e
T
i
e
i
C
N
X
iD1
b
ii
e
T
i
e
i
!
C 2L
N
X
iD1
e
T
i
e
i
1
1
2
N
X
iD1
e
T
i
e
i
!
C b
2
N
X
iD1
e
T
i
e
i
!
C 2L
N
X
iD1
e
T
i
e
i
.
1
C 2b
2
C 4L/
1
2
N
X
iD1
e
T
i
e
i
!
: (17.8)
Let D
1
C 2b
2
C 4L,then
P
V.e/ V .e/ and
V.e
1
.t/; : : : ; e
N
.t// V
e
1
t
C
k1
;:::;e
N
t
C
k1
exp..t t
k1
//;
t 2 .t
k1
;t
k
; k D 1;2;::: (17.9)
On the other hand, it follows
V.e.t
C
k
// D
1
2
e
T
1
t
C
k
e
1
t
C
k
CCe
T
N
t
C
k
e
N
t
C
k
D
1
2
.C
k
e
1
.t
k
//
T
C
k
e
1
.t
k
/ CC.C
k
e
N
.t
k
//
T
C
k
e
N
.t
k
/
max
C
T
k
C
k
V.e.t
k
//
ˇ
k
V.e.t
k
//: (17.10)

210 X. Han and X. Fu
The following results come from (17.9)and(17.10).
For t 2 .t
0
;t
1
, V.e
1
.t/; : : : ; e
N
.t// V.e
1
.t
C
0
/;:::;e
=
n.t
C
0
// exp..t t
0
//;
which leads to V.e
1
.t
1
/;:::;e
N
.t
1
// V.e
1
.t
C
0
/;:::;e
N
.t
C
0
// exp..t
1
t
0
// and
V.e
1
.t
C
1
/;:::;e
N
.t
C
1
// ˇ
1
V.e
1
.t
1
/;:::;e
N
.t
1
// ˇ
1
V.e
1
.t
C
0
/;:::;e
N
.t
C
0
//
exp..t
1
t
0
//.
In general, for t 2 .t
k
;t
kC1
; .k D 0; 1; 2; /;
V.e
1
.t/; : : : ; e
N
.t// V.e
1
.t
C
0
/;:::;e
N
.t
C
0
//ˇ
1
:::ˇ
k
exp..t t
0
//:
Therefore, we have the following results.
(i) If <0and there exists a constant ˛.0 ˛</ such that ln ˇ
k
˛.t
k
t
k1
/ 0; k D 1;2;::::Then we obtain that for t 2 .t
k
;t
kC1
,
V.e
1
.t/; : : : ; e
N
.t//
V.e
1
.t
C
0
/;:::;e
N
.t
C
0
//ˇ
1
ˇ
k
exp..t t
0
//
D V.e
1
.t
C
0
/;:::;e
N
.t
C
0
//ˇ
1
ˇ
k
exp.˛.t t
0
// exp.. C ˛/.t t
0
//
V.e
1
.t
C
0
/;:::;e
N
.t
C
0
//ˇ
1
ˇ
k
exp.˛.t
k
t
0
// exp.. C ˛/.t t
0
//
D V.e
1
.t
C
0
/;:::;e
N
.t
C
0
//ˇ
1
exp.˛.t
1
t
0
//ˇ
2
exp.˛.t
2
t
1
//
ˇ
k
exp.˛.t
k
t
k1
// exp.. C ˛/.t t
0
//
V.e
1
.t
C
0
/;:::;e
N
.t
C
0
// exp.. C ˛/.t t
0
//:
Namely, V.e
1
.t/; : : : ; e
N
.t// V.e
1
.t
C
0
/;:::;e
N
.t
C
0
// exp.. C ˛/
.t t
0
//; t t
0
. We can conclude that the trivial solution of system (17.7)
is globally exponentially stable from the theories in [2, 10, 22]. That is
e
i1
;:::;e
in
! 0.i D 1; 2; N / as t !1. Then, complex networks (17.5)
synchronize up with each node quickly with above impulsive control inputs.
(ii) If 0 and there exists a constant ˛ 1, such that ln.˛ˇ
k
/ C .t
kC1
t
k
/ 0; k D 1;2;:::.Fort 2 .t
k
;t
kC1
,thenV.e
1
.t/; : : : ; e
N
.t//
V.e
1
.t
C
0
/;:::;e
N
.t
C
0
//ˇ
1
ˇ
2
ˇ
k
exp..t t
0
//
V.e
1
.t
C
0
/;:::;e
N
.t
C
0
//ˇ
1
ˇ
2
ˇ
k
exp..t
kC1
t
0
//
V.e
1
.t
C
0
/;:::;e
N
.t
C
0
//ˇ
1
exp..t
2
t
1
//ˇ
2
exp..t
3
t
2
//
ˇ
k
exp..t
kC1
t
k
// exp...t
1
t
0
//
V.e
1
.t
C
0
/;:::;e
N
.t
C
0
//
1
˛
k
exp...t
1
t
0
//;
which implies that the conclusion (ii) of Theorem 2 holds. That is complex networks
achieve synchronize. ut
Remark. The solution of system (17.6) exists if the conditions in Theorem 2 hold
for system (17.5). That is, the impulsive system (17.6) is soluble.

17 Impulsive Control Induced Effects on Dynamics of Complex Networks 211
The following theorem can be derived for system (17.5):
Theorem 3. Suppose that conditions in Theorem 2 are satisfied by impulsive
differential system (17.5). And impulsive input functions are taken as
I
k
.z
k
;x
i
/ D H.z
k
C "x
i
/ x
i
D z
k
B
k
C C
k
x
i
x
i
;i D 1;2;:::;N;
where z
kC1
D g.z
k
/; k D 0; 1; 2; : : : , then we have
(a) (1) H.0/ D g.0/ D f.0/ D 0; the map H is a topological transmission from
D ! D, which is defined in C
2
; (2) The map g W Y ! Y D is a chaotic
map in C
2
in the Devaney sense, and Y is compact.
Then, the system (17.6) is also chaotic in the Devaney sense as D 0 if
conditions .1/ and .2/ hold.
(b) If the series fz
k
g.k D 0; 1; 2; : : :/ is . 1/-period, that is z D g
.z/ (for all
z 2fz
k
g) and g./ is continuous, complex networks (17.5) synchronize, and the
synchronization manifold s.t/ is T -period, that is s.t/ D s.t CT/, for any
t 2 Œ0; C1/.
It can be seen from numerical simulations that the synchronization orbit of com-
plex networks may be an equilibrium point as 0< 1, periodic orbits as
1<<3:5, or a chaotic orbit as > 3:57.
17.3 Numerical Simulations
To demonstrate the above-derived theoretical results, some typical examples of
chaotic systems are used as the dynamical node of the impulsively coupled sys-
tem. Such as the typical Lorenz system etc.
A single Lorenz system is described by
8
<
:
Px
i1
D c
1
.x
i2
x
i1
/;
Px
i2
D c
3
x
i1
x
i1
x
i3
x
i2
;
Px
i3
D x
i1
x
i2
c
2
x
i3
:
(17.11)
When c
1
D 10; c
2
D
8
3
;c
3
D 28; Lorenz system has a chaotic attractor.
Then we have
A D
2
4
10 10 0
28 10
00
8
3
3
5
; D
2
4
0:100
000
000
3
5
;
and
1
D
max
..A C b
ii
/
T
C .A C b
ii
// D 27:2938: We can obtain that the
bound of above chaotic system is 39:2462. The nonlinear part of the system is
'.x
i1
;x
i2
;x
i3
/ D .0; x
i1
x
i3
;x
i1
x
i2
/
T
. It follows that L in theorem is 39:2462.

212 X. Han and X. Fu
Consider the coupled systems with four Lorenz systems as the ring chain,
where B D
2
6
6
4
10 0 1
0 11 0
0011
1001
3
7
7
5
: For the case, choose the matrix B
k
D .0;1;0/;
C
k
D .0:1; 0:1; 0:1/ and ˛ D1:01; ˇ D 0:01;
2
D 1; D 186:9592 the same value
as before. The impulsive interval for synchronization should be less than 0:0246.
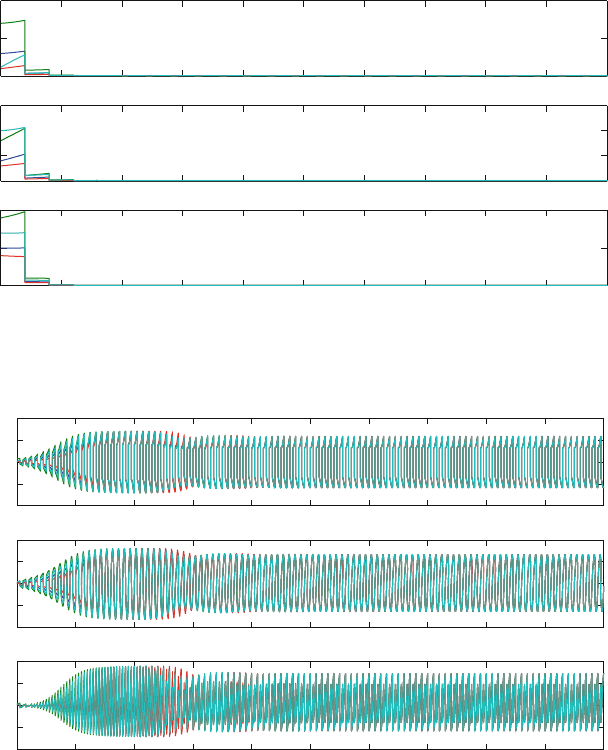
Then, Figs. 17.1–17.3 show the stable of the origin solution of the four Lorenz
0 5 10 15 20 25 30 35 40 45 50
−20
−10
0
10
20
0 5 10 15 20 25 30 35 40 45 50
−40
−20
0
20
40
0 5 10 15 20 25 30 35 40 45 50
0
20
40
60
t/s
x
i1
(t)(i=1,2,3,4)x
i2
(t)(i=1,2,3,4)x
i3
(t)(i=1,2,3,4)
Fig. 17.1 Variable state of the ring networks with four Lorenz coupled without impulsive control
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
x
i1
(t)(i=1,2,3,4)x
i2
(t)(i=1,2,3,4)x
i3
(t)(i=1,2,3,4)
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
t/s
0
5
10
0
5
10
15
0
5
10
Fig. 17.2 Variable state of the ring networks with four Lorenz coupled for D 0:5
17 Impulsive Control Induced Effects on Dynamics of Complex Networks 213
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
x
i1
(t)(i=1,2,3,4)x
i2
(t)(i=1,2,3,4)x
i3
(t)(i=1,2,3,4)
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
t/s
0
5
10
0
5
10
15
0
5
10
Fig. 17.3 Variable state of the ring networks with four Lorenz coupled D 1
0 1 2 3 4 5 6 7 8 9 10
x
i1
(t)(i=1,2,3,4)x
i2
(t)(i=1,2,3,4)x
i3
(t)(i=1,2,3,4)
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
t/s
−100
−50
0
50
100
−200
−100
0
100
200
−200
−100
0
100
200
Fig. 17.4 Synchronization of the variable states of the networks with four Lorenz coupled for
D 3:5
systems coupled. Figures 17.4–17.6 display the synchronization and the node dy-
namics of the coupled networks with four Lorenz systems as D 3:5.
It can be seen from the numerical simulations that ring networks with four Lorenz
system coupled cannot achieve synchronization for certain given values of cou-
pling strength matrix . It is shown by Fig.17.1. However, the networks (17.2)
will be stable to origin quickly with the presented impulsive control, where the
impulsive response is corresponding with the outer input variables. Figures 17.2

214 X. Han and X. Fu
8
8.2 8.4 8.6 8.8
9
9.2 9.4 9.6 9.8 10
x
i1
(t)(i=1,2,3,4)x
i2
(t)(i=1,2,3,4)x
i3
(t)(i=1,2,3,4)
8 8.2 8.4 8.6 8.8 9 9.2 9.4 9.6 9.8 10
8 8.2 8.4 8.6 8.8 9 9.2 9.4 9.6 9.8 10
t/s
−100
−50
0
50
100
−200
−100
0
100
200
−200
−100
0
100
200
Fig. 17.4 (continued)
0 1 2 3 4 5 6 7 8 9 10
−20
0
20
x
11
−x
21
x
12
−x
22
x
13
−x
23
0 1 2 3 4 5 6 7 8 9 10
−50
0
50
0 1 2 3 4 5 6 7 8 910
−100
−50
0
50
t/s
Fig. 17.5 The synchronization errors between the first and second node of the four Lorenz coupled
networks for D 3:5
and 17.3 display the stable of the origin of networks. And the synchronization man-
ifold can be changed with the outer input impulsive functions. The same conclusions
can be obtained for the synchronizing coupling strengths, that is, the synchroniza-
tion manifold is changed with impulsive inputs.
