Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay

Подождите немного. Документ загружается.

182 H. Shang

region of the basin is performed continuously until there is only a trivial point (see

Fig. 15.1l). Accordingly, the change of the topological structure of the safe basin in

Fig. 15.1 conﬁrms that a short delay can reduce but a long delay may aggravate the

fractal erosion of the safe basin.

Figure 15.2 shows the change of the boundary and range of the safe basin of

(15.2)whenG D 0:3 and the delay varies. It is drawn in a similar way to Fig. 15.1.

For  D 0, the safe basin is not smooth and the range is small as shown in Fig. 15.2a.

With  varying from 0 to 13=25 (see Fig. 15.2a–d), the area of the safe basin

increases with delay though the boundary of the safe basin is still not smooth. With

the delay increasing further, the safe basin begins to shrink and the ﬁngers occur

in the boundary (see Fig. 15.2e–h), which suggests the fractal behavior. And such

erosion in the inner region of the basin is performed continuously until there is only

a trivial point as the safe basin (see Fig. 15.2h). Similar to the case for G D 0:1,it

follows from Fig. 15.2 that a small value of the time delay is helpful to enlarge the

safe basin, but a large value provides the opposite action or aggravates the erosion.

15.3 Effects of the Delay on the Area of the Safe Basin

Figures 15.1 and 15.2 indicate that the delay can reduce the erosion or enlarge the

extent of safe basins of (15.2). However, the evolution of safe basins with the delay

is not simple. When the delay is long enough, it can lead to the sudden erosion of

the safe basin. To quantify those phenomena displayed in Figs. 15.1 and 15.2,we

deﬁne that the area of the “initial basin” is 100% for c D 0:01; G D 0,and D 0

in (15.2)(seeFig.15.3), since the basin boundary is smooth. Then the change of the

basin area with the amplitude G for the different levels of the delay can be observed

in Fig. 15.4 where c D 0:01; ˝ D 1:0,andG varies from 0 to 0.8.

For A D0:2 (the dashing-dot line in Fig. 15.4), the area of the safe basin with

delayed position feedback control is smaller than that without control. For A D 0:2

(solid lines in Fig. 15.4), the area of the safe basin under delayed position feedback

for a small value of the amplitude is bigger than the uneroded “initial basin,” which

show the erosion of the safe basin is successfully reduced. The area of the safe

basin of the system (15.2) decreases with the increasing of the amplitude under

Fig. 15.3 The initial safe basin

15 Control of Safe Basin by Delayed Feedbacks 183

Area (%)

0.2 0.4 0.6 0.8

τπ

100

150

Fig. 15.4 Variation of the basin area with the increasing the amplitude of the excitation for the

system (15.2) under different values of time delay where A D 0:2 for solid lines and A D0:2

for the dashing-dot line

each different value of the delay. As time delay increases from 0, the basin area is

ﬁrst enlarged to maximum value and then shrink (see the solid lines  D 4=5 and

 D ). Besides, the comparison of the solid lines  D 0 and  D =5 shows that

a small delay can control the basin erosion under different values of G when A is

positive.

When the delay is short, it is worthwhile to expand the delay variable x.t / in

a Taylor series despite occasional warnings [15]. One can write

x.t  / D x.t/   Px.t/ C (15.3)

Substituting (15.3)in(15.2), one can obtain that



Px D y;

Py D.c C A/y  x C x

C G cos t:

(15.4)

The unperturbed system can be expressed as



Px D y;

Py Dx C x

;

(15.5)

which is a Hamiltonian system. Then the system has a hetero-clinic orbit to two-

saddle points .1; 0/ and (1, 0), which can be given by

x.t/ D tanh

t; y.t/ D˙

sech

t: (15.6)

184 H. Shang

Obviously, when the feedback gain A is positive, the system (15.4) can be

considered as the system (15.1) with a larger damping. As we know, the increasing

of the damping can reduce the erosion of safe basins [9, 10]. Therefore, one can

explain why the safe basin in (15.2) is enlarged when the delay increases from 0.

Besides, one can also conclude that the safe basin in (15.2) will be eroded when the

feedback gain is negative and the delay increases from 0, which is veriﬁed by the

dashing-dot line in Fig. 15.4.

15.4 Conclusions

Some investigation has been made on the evolution of the broaching attracting basin

of a nonlinear yaw equation model of a ship with delayed position feedbacks. The

fourth Runge-Kutta and Monte Carlo methods are employed to observe effects on

safe basins when time delay is considered as the control parameter. For a short delay,

the mechanism of the evolution of safe basin is analyzed. Some important results are

obtained as below:

(a) Similar to the case in ordinary differential system, the increasing of excitation

amplitude can lead to the erosion of the safe basin under delayed position feed-

back control.

(b) The basin area is not a monotonic function of the delay for the delayed position

feedback control.

safe basins. For positive feedbacks, the delay can be indeed used to reduce the

erosion of safe basins. The erosion can be reduced when the delay is short, but

a long time delay makes the erosion more sudden and severe.

(d) The sudden erosion of the safe basin caused by the increasing of the delay in

delayed position feedback controlled system can be ascribed to the hetero-clinic

tangency of the manifolds. It is well known that the hetero-clinic tangency of

the stable and unstable manifolds may yield chaos. The results provide the pos-

sibility to control chaos that occurs in the system.

Acknowledgments This work is supported by Shanghai Municipal Education Commission under

Grant No. YYY08004, Shanghai Leading Academic Discipline Project under Grant No. J51501,

and National Natural Science Foundation of China under Grant No. 10902071.

References

1. Freitas M, Viana R, Grebogi C (2003) Erosion of the safe basin for the transversal oscillations

of a suspension bridge. Chaos Solitons Fractals 18(4):829–841

2. Thompson J, Rainey F, Soliman MS (1995) Ship stability criteria based on chaotic transients

from incursive fractals. Philos Trans R Soc Lond A 332(1):149–167

3. Thompson J, McRobie F (1993) Indeterminate bifurcation and the global dynamics

of driven oscillators. In: Proceedings of 1st European nonlinear oscillation’s confer-

ence. Hamburg, Germany

15 Control of Safe Basin by Delayed Feedbacks 185

4. Senjanovic I, Parunov J, Cipric G (1997) Safety analysis of ship rolling in rough sea. Chaos

Solitons Fractals 8(4):659–680

5. Soliman M (1995) Fractal erosion of basins of attraction in coupled nonlinear systems. J Sound

Vib 182(5):729–740

6. Soliman M, Thompson J (1989) Intergrity measures quantifying the erosion of smooth and

fractal basins of attraction. J Sound Vib 35(3):453–475

7. Rega G, Lenci S (2005) Identifying, evaluating, and controlling dynamical integrity measures

in non-linear mechanical oscillators. Nonlinear Anal 63(5–7):902–914

8. Gan C (2005) Noise-induced chaos and safe basin in softening Dufﬁng oscillator. Chaos

Solitons Fractals 25(5):1069–1081

9. Bishop S, Galvanetto U (1993) The inﬂuence of ramped forcing on safe basins in a mechanical

oscillator. Dyn Stab Syst 8(2):73–80

10. Moon F, Li G (1985) Fractal basin boundaries and homoclinic orbits for periodic motion in a

two-well potential. Physica Rev Lett 55(14):1439–1442

11. Xu J, Lu Q, Huang K (1996) Controlling erosion of safe basin in nonlinear parametrically

excited systems. Acta Mechanica Sin 12(3):281–288

12. Shang H, Xu J (2008) Multiple periodic solutions in Lienard oscillator with delayed position

feedbacks. J Tongji Univ (Nat Sci) 36(7):962–966

13. Xu J, Chung K (2003) Effects of time delayed position feedback on a van der Pol–Dufﬁng

oscillator. Physica D 180(1–2):17–39

14. Maccari A (2006) Vibration control for parametrically excited Li´enard systems. Nonlinear

Mech 41(1):146–155

15. Driver D (1977) Ordinary and delay differential equations. Springer, New York

Part III

Switching and Stochastic

Dynamical Systems

Chapter 16

On Periodic Flows of a 3-D Switching System

with Many Subsystems

Albert C.J. Luo and Yang Wang

Abstract In this chapter, the stability and bifurcation of periodic ﬂows in a

switching system of multiple subsystems with transport laws at switching points

is presented. The periodic ﬂows and stability for linear switching systems are

discussed as an example. Analytical prediction of the periodic ﬂow in such lin-

ear switching systems is carried out and parameter maps of stability are given.

The methodology presented in this chapter can be applied to nonlinear switching

systems. The further results on chaos, stability, and bifurcation of periodic ﬂows in

nonlinear switching systems will be presented in sequel.

16.1 Introduction

Consider a C

-continuous system (r

>1) on an open domain D

 R

,inthe

time interval t 2 Œt

k1



.i/

D F

.i/



.i/

;t;p

.i/



2 R

I x

.i/



.i/

; x

.i/

;:::;x

.i/



2 D

: (16.1)

The time is t and

.i/

D dx

.i/

=dt. p

.i/



.i/

;:::;p

.i/



2 R

is a

parameter vector. On the domain D

 R

, the vector ﬁeld F

.i/



.i/

;t;p

.i/



with

the parameter vector p

.i/

is C

-continuous in x

.i/

for time interval t 2 Œt

k1

.

With an initial condition x

.i/

k1

/ D x

.i/

k1

, the dynamical system in (16.1)

possesses a continuous ﬂow as

.i/

.t/ D ˆ

.i/



.i/

k1

;t;p

.i/



I x

.i/

k1

D ˆ

.i/



.i/

k1

; p

.i/



: (16.2)

A.C.J. Luo (



)

Department of Mechanical and Industrial Engineering, Southern Illinois University Edwardsville,

Edwardsville, IL62026-1805, USA

e-mail: aluo@siue.edu

A.C.J. Luo (ed.), Dynamical Systems: Discontinuity, Stochasticity and Time-Delay,

DOI 10.1007/978-1-4419-5754-2

16,

 Springer Science+Business Media, LLC 2010

189

190 A.C.J. Luo and Y. Wang

To investigate the switching system consisting of many subsystems, the following

assumptions of the ith subsystem should be held.

(A1)

.i/



.i/

;t;p

.i/



2 C

I ˆ

.i/



.i/

;t;p

.i/



2 C

Ion D

for t 2 Œt

k1

;

(16.3)

(A2)

jjF

.i/

jjK

.i/

.const/Ijjˆ

.i/

jj  K

.i/

.const/ on D

for t 2 Œt

k1

; (16.4)

(A3)

.i/

D ˆ

.i/

.t/ … @D

for t 2 .t

k1

/: (16.5)

(A4) The switching of any two subsystems possesses the time continuity.

To investigate the switching system, a set of dynamical systems in ﬁnite time in-

tervals will be introduced ﬁrst. From such a set of dynamical systems, the dynamical

subsystems in a resultant switching system can be selected.

Deﬁnition 1. From dynamical systems in (16.1), a set of dynamical systems on

the open domain D

in the time interval t 2 Œt

k1

 for i D 1;2;:::;mis deﬁned



i D 1;2;:::;m

; (16.6)

where



(

.i/

D F

.i/



.i/

;t;p

.i/



2 R

.i/

2 D

 R

; p

.i/

2 R

.i/

k1

/ D x

.i/

k1

It 2 Œt

k1

Ik 2 N

)

(16.7)

From Assumptions (A1)–(A3), the subsystem possesses a ﬁnite solution in the ﬁnite

time interval and such a solution will not reach the corresponding domain boundary.

From the set of subsystems, the corresponding set of solutions for such subsystems

can be deﬁned as follows.

Deﬁnition 2. For the ith dynamical subsystems in (16.1), with an initial condition

.i/

k1

2 D

for k 2 N and, there is a unique solution x

.i/

.t/ D ˆ

.i/



.i/

k1

;t;p

.i/



For all i D 1;2;:::;m, a set of solutions for the i th subsystem in (16.1) on the open

domain D

in the time interval t 2 Œt

k1

 is deﬁned as

S D

‚

.i/

i D 1;2;:::;m

; (16.8)

where

‚

.i/



.i/

.t/

.i/

.t/ D ˆ

.i/



.i/

k1

;t;t

k1

; p

.i/



I t 2 Œt

k1

; k 2 N

(16.9)

16 On Periodic Flows of a 3-D Switching System with Many Subsystems 191

This class of switching systems exists in network systems and control systems [1]

and widely applied to electronic power systems [2]. The survey of such switch-

ing systems can be referred to [3]. To obtain the complex responses of switching

systems, numerical schemes can be developed. For instance, Danca [4]usedan

explicit Euler method to give a numerical integration scheme for switching dynami-

cal systems to obtain approximate numerical solutions. Grune and Kloeden [5]used

the Taylor series scheme to develop a higher order numerical integration scheme to

carry out numerical simulations of switching systems. Gokcek [6] used the Floquet

theory to discuss the stability of switching systems. Indeed, approximate numerical

methods can help one understand the behaviors of switching systems. However, for

the traditional analytical and numerical methods, it is very difﬁcult to handle the

discontinuity for the switching of two systems, and it is impossible to provide an

accurate solution for switching systems. In 2005, Luo [7] developed a local theory

of singularity for such switching systems in order to exactly switch from a subsys-

tem to another subsystem (also, see Luo [8]). In 2008, Luo and Wang [9]presented

a general concept of switching systems to investigate switching dynamics of multi-

ple linear oscillators. With periodic and random piecewise forcing, the solutions of

dynamical oscillation were presented. Periodic motions of switching systems with

vector ﬁeld switching were investigated. This chapter will apply the methodology

for switching system in Luo and Wang [9] to 3-D switching dynamical systems. The

periodic ﬂow and corresponding stability of the 3-D switching system will be inves-

tigated. The parameter map for the 3-D linear switching systems will be presented

and numerical illustrations for periodic ﬂow will be carried out.

16.2 Methodology for Periodic Flows

To describe the switching of subsystems, consider a switching set for the i th

subsystem to be

†

.i/

D x

.i/

/; k D 0; 1; 2; : : :

: (16.10)

From the solution of the i th subsystem, a mapping P

for a time interval Œt

k1



is deﬁned as

W †

.i/

! †

.i/

or P

W x

.i/

k1

! x

.i/

for i D 1;2;:::;m: (16.11)

Deﬁne a time difference parameter for the ith subsystem for time interval Œt

k1



.i/

D t

 t

k1

(16.12)

which is set arbitrarily. For simplicity, introduce two vectors herein

.i/



.i/

; f

.i/



I x

.i/



.i/

;:::;x

.i/



: (16.13)

192 A.C.J. Luo and Y. Wang

From the solution in (16.9)fortheith subsystem, the foregoing equation gives for

(i D 1;2;:::;m)

.i/



.i/

; x

.i/

k1



D x

.i/

 ˆ

.i/



.i/

k1

; p

.i/



D 0: (16.14)

Suppose the two trajectories of the ith and j th subsystems in phase space at the

switching time t

is continuous, i.e., for i; j 2f1;2;:::;mgat time t

.j /

D x

.i/



.i/

1;k

;:::;x

.i/

m;k





.j /

1;k

;:::;x

.j /

m;k



(

16.15)

If the two solutions of the i th and j th subsystems at the switching time t

are dis-

continuous, for instance, an impulsive system needs a transport law. From Luo [2],

a vector for the transport law is introduced as

.ij/



.ij/

;:::;g

.ij/



(16.16)

so the transport law between the ith and j th subsystems can be written as

.ij/



.i/

; x

.j /



D 0 at time t

: (16.17)

In other words, one obtains

.j /

1.k/

D g

.ij/



.i/

1.k/

;:::;x

.i/

m.k/



.j /

2.k/

D g

.ij/



.i/

1.k/

;:::;x

.i/

m.k/



;



.j /

m.k/

D g

.ij/



.i/

1.k/

;:::;x

.i/

m.k/



; for i;j 2f1;2;:::;mg:

;

: (16.18)

From the transport law, a transport mapping is introduced as for i; j 2f1;2;:::;mg

.ij/

W †

.i/

! †

.j /

; (16.19)

i.e.,

.ij/

.i/

.j /

or P

.ij /



.i/

1.k/

;:::;x

.i/

m.k/





.j /

1.k/

;:::;x

.j /

m.k/



:(16.20)

P D P

nC1

ı P

ııP

ı P

 P

:::l

(16.21)

The algebraic equations for the transport mapping are given in (16.18). The mapping

for the ith subsystem for time t 2 Œt

k1

 and the transport mapping at time

t D t

are sketched in Figs. 16.1 and 16.2. The initial and ﬁnal points of mapping P

are x

.i/

k1

and x

.i/

. Similarly, the initial and ﬁnal points of mapping P

are x

.j /

and

.j /

kC1

. The mappings relative to the subsystem are sketched by a solid curve. The

two mappings are connected by a transport mapping at t D t

, which is depicted

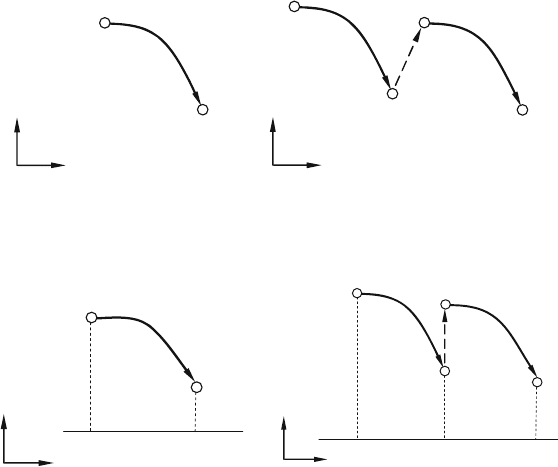
16 On Periodic Flows of a 3-D Switching System with Many Subsystems 193

−

(ij)

(i )

−

(i )

( j)

(i )

Fig. 16.1 (a) Mapping P

and (b) transport mapping P

.ij/

in phase plane (n

D n)

(i)

−

(i)

−

( j)

(i)

−

(ij)

Fig. 16.2 (a) Mapping P

and (b) transport mapping P

.ij/

in the time history

by the dashed line. In phase plane, there is a nonnegative distance governed by

(16.17). However, the time-history of ﬂows for the switching system experiences a

jump at time t D t

. If the transport law gives a special case to satisfy (16.14), the

solutions of two subsystems are C

-continuous at the switching time t D t

.The

jump phenomenon will disappear. Consider a ﬂow of the resultant switching system

to have a mapping structure for t 2[

j D1



kCj 1

kCj



as where

i D 1;2;:::;n

: (16.22)

Consider an initial state x



1.k/

;:::;x

m.k/



at t D t

and ﬁnal state

nC1

kCn



nC1

1.kCn/

;:::;x

nC1

m.kCn/



at t D t

kCn

, respectively.

nC1

kCn

D P x

D P

nC1

ı P

ııP

ı P

: (16.23)

with each time difference, one has the total time difference

kCn

 t

mD1

kCm

: (16.24)