Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay
Подождите немного. Документ загружается.


226 Y. J i n
From (19.2)–(19.6), one can see that the introduction of the non-Gaussian noise
involves many mathematical difficulties. Thus, the following Gaussian noise ap-
proximation in the region
j
q 1
j
1 (q>1and q<1) is adopted by applying
the path integral approach [21–22]
1
dV
q
./
d
D
1 C
D
.q 1/
2
2
1
"
1 C
D
.q 1/
˝
2
˛
2
#
1
D
1
eff
;
(19.8)
where
eff
D .2.2 q/=.5 3q//.
It is easy to see that (19.2) can be rewritten as a re-normalized Ornstein–
Uhlenbeck process with the effective noise correlation time
eff
and the effective
multiplicative noise intensity D
eff
D .2.2 q/=.5 3q//
2
D. Especially, when
q ! 1,thereare
eff
! and D
eff
! D.
Based on (19.8), (19.2) has been transformed into a Markov process. And using
the unified colored noise approximation, (19.7) can be rewritten as
Px D
2. e
x
/
1 C 2e
x
eff
C
2
1
eff
Œ1 C 2e
x
eff
.t/; (19.9)
where
eff
is defined as (19.8).
The corresponding Fokker–Plank equation determined by (19.9) can be
derived as
@P .x ; t /
@t
D
@
@x
ŒA.x/P .x; t/ C
@
2
@x
2
ŒB.x/P.x; t/; (19.10)
where
A.x/ D
2. e
x
/
1 C 2
eff
8e
x
eff
.1 C 2e
x
eff
/
3
D
eff
;B.x/D
4D
eff
.1 C 2e
x
eff
/
2
:
Substituting the transformation x D ln I , the stationary probability distribution
(SPD) of the laser intensity can be obtained from (19.10)
st
.I / D
N
B.I/
exp
ˆ.I /
D
; (19.11)
where
ˆ.I / D
5 3q
2 q
2
. ln I CI/
8
.2 q/I.2 I/
4.5 3q/
;
B.I/ D
2.2 q/I
.5 3q/ C 4.2 q/I
(19.12)

19 Non-equilibrium Phase Transitions in a Single-Mode Laser Model 227
and N is a normalization constant. When q D 1,(19.11) is consistent with the result
obtained in [4].
From (19.11)–(19.12), the extremal equation of the SPD
st
.I / are determined
by the following equation of third order
I
3
C a
2
I
2
C a
1
I C a
0
D 0; (19.13)
where
a
0
D
1
16
8D.2 q/
2
.5 3q/
2
2
.2 q/
2
;
a
1
D
1
16
.5 3q/Œ.5 3q/ 8.2 q/
2
.2 q/
2
;
a
2
D
1
2
.5 3q/ 2.2 q/
.2 q/
:
When the form of
st
.I / changes between the bimodal structure and the unimodal
structure, the critical parameter D
c
satisfies the following equation
D
c
D
2
216
4 C
.5 3q/
.2 q/
3
: (19.14)
That is, when the correlation time is fixed, the SPD is bimodal for D>D
c
and
it is unimodal for D<D
c
. Equation (19.14) can be rewritten according to the
effective noise correlation time
eff
and the effective multiplicative noise intensity
D
eff
as
D
eff
D
2
eff
27
.2 C
1
eff
/
3
: (19.15)
19.3 General Analysis
From (19.11)and(19.15), the effects of the non-Gaussian noise on the non-
equilibrium phase transition of the single-mode laser are discussed in this section.
In Fig. 19.1, the transition lines for different values of q are plotted in the .; D/
plane. It is seen that the transition line decreases with the increase of q and a min-
imum value of noise intensity D is needed to induce the phase transition. When
.; D/ falls into the region above the transition line, the extreme equation (19.13)
has three extreme points. Otherwise, (19.13) only has one extreme point. The cor-
responding SPD
st
.I / is plotted with different values of q shown in Fig. 19.2.In
Fig. 19.2, the noise correlation time and the noise intensity D are fixed as D 1
and D D 0:5, which are chosen above the boundary of q D 1:5 and below the
boundaries of q D 1 and q D 0:5. The SPD
st
.I / corresponding to q D 1 and
q D 0:5 has a single peak when the laser intensity I in interval [0,1]. When q D 1:5,
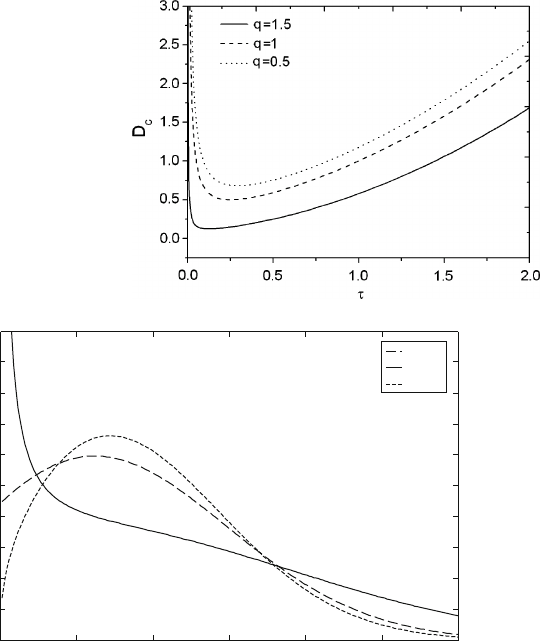
228 Y. J i n
Fig. 19.1 Phase diagram D
c
vs. for different values of q
with D 1
0 0.5 1 1.5 2 2.5 3
I
ρ
st
(I)
q=1
q=1.5
q=0.5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Fig. 19.2 The SPD
st
.I / for different values of q with D 1, D D 0:5; D 1
the curve of
st
.I / exists an infinite maximum at I D 0 and a finite maximum at
0<I <1. The SPD
st
.I / appears a bimodal structure and the corresponding
extreme equation (19.13) has two maximum points and one minimum point, which
is consistent with the results shown in Fig. 19.1. Thus, the SPD
st
.I / can switch
from unimodal to bimodal structure by increasing the parameter q for fixed and D.
Therefore, the parameter q plays an important role in the noise induced transitions.
Figure 19.3 gives the transition line for the case of q D 1:5. Points A and C
are chosen from the region below the transition line, while point B is laid above
the transition line. The SPD
st
.I / for the points A, B, C indicated in Fig. 19.3 are
presented in Fig. 19.4. The SPD
st
.I / at point A appears a bimodal structure. Then
fixed the value of the correlation time and increased the noise intensity D beyond
some threshold phase, the SPD
st
.I / corresponding to B has a unimodal structure.
If further fixed the noise intensity D and increased the correlation time beyond

19 Non-equilibrium Phase Transitions in a Single-Mode Laser Model 229
Fig. 19.3 Phase diagram D
c
vs. for q D 1:5 and D 1
0 0.5 1 1.5 2 2.5 3
I
ρ
st
(I)
corresponding to ponit A
corresponding to point C
corresponding to point B
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Fig. 19.4 The SPD
st
.I / for different combinations of .; D/ with D 1 and q D 1:5
some threshold value, the SPD
st
.I / corresponding to C goes back to the bimodal
structure. This type of non-equilibrium transition phenomenon is called reentrance
phenomenon. Thus, the reentrance phenomenon is found in this laser model when
the noise source is the non-Gaussian noise.
19.4 Conclusion Remarks
The non-equilibrium phase transition of a single-mode laser model driven by non-
Gaussian noise is studied in this paper. The stationary probability distribution (SPD)
and its extremal equation are derived by using the path integral approach and the
230 Y. J i n
unified colored noise approximation. It is found that there is a critical relation
between the noise intensity and the correlation time so that there is a transition line
separating the mono-stable region and the bi-stable region. Given the noise intensity
and the correlation time, the single-mode laser system undergoes a successive phase
transition by varying the departure of the non-Gaussian noise from the Gaussian
noise. Meanwhile, as indicated in the phase diagram, for some regions of values of
noise intensity and correlation time, the system turns to a bi-stable phase. Then, for
fixed value of correlation time and increased noise intensity beyond some thresh-
old value, the system undergoes a transition to a mono-stable phase. If the noise
intensity is further fixed and the correlation time is increased beyond some thresh-
old value, the system goes back to a bi-stable phase. This type of non-equilibrium
transition phenomenon is called reentrance phenomenon.
The single-mode laser model with random fluctuation is a particular prototype in
describing the effects of noises and may be subject to various kinds of noise sources.
This study, therefore, extends the application of the single-mode laser model by
introducing the non-Gaussian noise. The phenomena found in this paper provide a
basis for experimental research and technological applications of the laser system.
Acknowledgments This work was supported in part by the National Natural Science Foundation
of China under Grant Nos. 10702025, 10972032, and 70771005, in part by the Excellent Young
Scholars Research Fund of Beijing Institute of Technology under Grant No. 2008Y0175, Beijing
Municipal Commission of Education Project under Grant No. 20080739027, and the Ministry of
Education Foundation of China under Grant No. 20070004045.
References
1. Nicolis G, Prigogine I (1976) Selforganization in nonequilibrium system. Wiley, New York
2. Haken H (1977) Synergetics. Springer, Berlin
3. Horsthemke W (1984) Noise-induced transitions. Springer, New York
4. Hu G (1994) Stochastic force and nonlinear systems. Shanghai Science and Technological
Education Publishing House, Shanghai
5. Fulinski A (1995) Relaxation, noise-induced transitions, and stochastic resonance driven by
non-Markovian dichotomic noise. Phys Rev E 52:4523
6. Zhu SQ (1989) Multiplicative colored noise in a dye laser at steady state. Phys Rev A 40:3441
7. Gudyma YV (2004) Nonequilibrium first-order phase transition in semiconductor system
driven by colored noise. Physica A 331:61
8. Van den Broeck C, Parrondo JMR, Toral R (1994) Noise-induced nonequilibrium phase tran-
sition. Phys Rev Lett 73:3395
9. Zaikin AA, Garcia-Ojalvo J, Schimansky-Geier L (1999) Nonequilibrium first-order phase
transition induced by additive noise. Phys Rev E 60:R6275
10. Castro F, Sanchez AD, Wio HS (1995) Reentrance phenomena in noise induced transitions.
Phys Rev Lett 75:1691
11. Jia Y, Li JL (1997) Reentrance phenomena in a bistable kinetic model driven by correlated
noise. Phys Rev Lett 78:994
12. Zhu SQ (1990) White noise in dye-laser transients. Phys Rev A 42:5758
13. Cao L, Wu DJ, Lin L (1994) First-order-like transition for colored saturation models of dye
lasers: effects of quantum noise. Phys Rev A 49:506
19 Non-equilibrium Phase Transitions in a Single-Mode Laser Model 231
14. Cao L, Wu DJ (1999) Cross-correlation of multiplicative and additive noises in a single-mode
laser white-gain-noise model and correlated noises induced transitions. Phys Lett A 260:126
15. Liang GY, Cao L, Wu DJ (2002) Moments of intensity of single-mode laser driven by additive
and multiplicative colored noises with colored cross-correlation. Phys Lett A 294:190
16. Luo XQ, Zhu SQ, Chen XF (2001) Effects of colored noise on the intensity and phase in a laser
system. Phys Lett A 287:111
17. Xie CW, Mei DC (2004) Effects of correlated noises on the intensity fluctuation of a single-
mode laser system. Phys Lett A 323:421
18. Jin YF, Xu W, Xie WX, Xu M (2005) The relaxation time of a single-mode dye laser system
driven by cross-correlated additive and multiplicative noises. Physica A 354:143
19. Bezrukov SM, Vodyanoy I (1997) Stochastic resonance in non-dynamical systems without
response thresholds. Nature 385:319
20. Goychuk I, H¨anggi P (2000) Stochastic resonance in ion channels characterized by information
theory. Phys Rev E 61:4272
21. Fuentes MA, Toral R, Wio HS (2001) Enhancement of stochastic resonance: the role of non-
Gaussian noises. Physica A 295:114
22. Fuentes MA, Wio HS, Toral R (2002) Effective Markovian approximation for non-Gaussian
noises: a path integral approach. Physica A 303:91
23. Revelli JA, Sanchez AD, Wio HS (2002) Effect of non-Gaussian noises on the stochastic
resonance-like phenomenon in gated traps. Physica D 168:165
24. Wio HS, Toral R (2004) Effect of non-Gaussian noise sources in a noise-induced transition.
Physica D 193:161
25. Goswami G, Majee P, Ghosh PK, Bag BC (2007) Colored multiplicative and additive non-
Gaussian noise-driven dynamical system: mean first passage time. Physica A 374:549

Chapter 20
Dynamical Properties of Intensity Fluctuation
of Saturation Laser Model Driven
by Cross-Correlated Additive
and Multiplicative Noises
Ping Zhu
Abstract Dynamical properties of the intensity fluctuation of a saturation laser
model driven by cross-correlated additive and multiplicative noises are investigated.
Using the Novikov theorem and the projection operator method, we obtain the an-
alytic expressions of the stationary probability distribution P
st
.I /, the relaxation
time T
c
, and the normalized correlated function C.s/ of the system. By numeri-
cal computation, we discussed the effects of the cross-correlated strength and the
cross-correlated time , the quantum noise intensity D, and the pump noise inten-
sity Q for the fluctuation of the laser intensity. Above the threshold, weakens the
stationary probability distribution, speeds up the startup velocity of the laser system
from start status to steady work, and enhances the stability of laser intensity out-
put; however, strengthens the stationary probability distribution and decreases the
stability of laser intensity output; when <0, speeds up the startup; on the con-
trary, when >0, slows down the startup. D and Q make the associated time
exhibit extremum structure, that is, the startup time possesses the least values. At the
threshold, cannot generate the effects for the saturation laser system, expedites
the startup velocity and enhances the stability of the startup. Below threshold, the
effects of and not only relate to and , but also relate to other parameters of
the system.
20.1 Introduction
Recently, people have been more and more interested in statistical fluctuations of
laser radiation which determine the limits on the use of lasers in almost every
application. The statistical properties of a sing-mode laser that contains both ad-
ditive and multiplicative noises are discussed by the experimental measurements
and theoretical analysis [1–7]. Meanwhile, importance of the saturation effects for
P. Z h u (
)
Department of Physics, Simao Teacher’s College, Puer 665000,
Peoples’s Republic of China
e-mail: zhuupp@yahoo.com.cn
A.C.J. Luo (ed.), Dynamical Systems: Discontinuity, Stochasticity and Time-Delay,
DOI 10.1007/978-1-4419-5754-2
20,
c
Springer Science+Business Media, LLC 2010
233
234 P. Z h u
the behavior of the laser is shown [8–12]. Zhu [13] discussed the saturation ef-
fects in a laser with additive and multiplicative white noises. Cao et al. [14–16]
analyzed the effects of saturation in the transient process of a dye laser with addi-
tive and multiplicative noises. Recently, the effects of correlations between additive
and multiplicative noises on the statistical fluctuation of a single-mode laser model
have attracted the close attention [7, 17–19]. In [7], Zhu investigated the steady-
state properties of the cubic model of single-mode laser with correlations between
additive noise and a multiplicative noise. Long et al. [18] studied the phase lock
induced by correlations between an additive noise and a multiplicative noise in the
cubic model of a single-mode laser. Liang at al. discussed moments of intensity of
single-model laser driven by additive and multiplicative colored noises with cross-
correlation [20].
The saturation laser model possessing the theoretical and applied values is as
typical as the cubic model of a single-mode laser model. In 1992, Zhu [21] investi-
gated the saturation effects of uncorrelated additive and multiplicative noises for a
saturation laser model. Thereafter, Zhu et al. [22,23] presented the correlation func-
tion and the relaxation time of a saturation laser model with correlated additive and
multiplicative white noises and discussed the effects of correlated white noises.
The associated relaxation time and the correlation function are important physi-
cal quantity to characterize the dynamic behavior of a stochastic process, and hence
are usually used to describe the fluctuation behavior of a nonlinear system. Re-
searches [24–27] on the problem have shown the important physical feature of the
associated relaxation time and the correlation function of the probability fluctua-
tion in a nonlinear stochastic system. Applying the means of the projection operator
method, Xie and Mei investigated the dynamical properties of a bistable kinetic
model with correlated white noises [28], and Mei et al. [29, 30] investigated the
effects of cross-correlation for the relaxation time and the correlated function of
a bistable system and showed the dynamical properties of a bistable system with
cross-correlated white noise. Zhu discussed the effects of cross-correlated additive
and multiplicative colored noise sources for the associated relaxation time and the
intensity correlation function of a bistable system [31, 32]. From these researches,
we found that the correlation strength between additive and multiplicative noises
play an important role in the processes of a nonlinear stochastic system. As the on-
going studying works further deepens, people have been more and more interested
in the stochastic system with cross-correlated additive and multiplicative colored
noises. Jin et al. [33] discussed the relaxation time of a single-mode dye laser sys-
tem driven by cross-correlated additive and multiplicative noises.The case of a full
account of the saturation with cross-correlated additive and multiplicative noises are
not further investigated.
This chapter is organized as follows: in Sect. 20.2, making use of the approx-
imatic Fokker–Plank equation (AFPE) for a saturation laser model with cross-
correlated additive and multiplicative noises, we solve the AFPE for stationary
probability distribution (SPD) of the laser system. Employing the means of the
projection operator method, in which the effects of the memory kernels are taken
into account, the analytic expressions of the associated relaxation time and the nor-
malized correlation function on the saturation laser model with cross-correlated

20 Dynamical Properties of Intensity Fluctuation 235
noises were derived. In Sect. 20.3, based on the numerical results, we discuss the
effects of the coupling strength , the cross-correlated tine , the quantum noise
intensity D, the pump noise intensity Q for the stationary probability distribution,
the associated relaxation time and the correlation function, so that we show further
dynamical properties of intensity fluctuation of saturation laser model driven by
cross-correlated additive and multiplicative noises. The discussion and conclusion
of the results conclude the paper.
20.2 Stationary Probability Distribution and Relaxation
Time and Correlated Function
The complex laser field E of a laser model with a full account of the saturation
effects follows the Langevin equation [8]
dE
dt
DkE C
F
1
E
1 C A j E j
2
=F
1
C
e
p.t/E C
e
q.t/; (20.1)
where K is the cavity decay rate for the electric field and F
1
D a
0
C K is the
gain parameter; a
0
and A are real and stand for net gain and self-saturation coeffi-
cients. The random variables
e
q.t/ and
e
p.t/ are complex and present the quantum
and pump noise.
Performing the polar coordinate transform E D re
i
on (20.1), one can obtain
two equation of the field amplitude r and phase . Then, the Langevin equation of
the field amplitude r can be written as follows [34]:
Pr DKr C
F
1
r
1 C
Ar
2
F
1
C
D
r
C rp.t / C q.t/: (20.2)
Defining the laser intensity is as I , and then we have I D r
2
.
Thus, (20.2) can be rewritten as the Langevin equation of I
P
I D2KI C
F
1
I
1 C
AI
F
1
C 2D C 2I
1
2
q.t/ C 2Ip.t/: (20.3)
The multiplicative noise p.t/ and the additive noise q.t/ are considered to be
Gaussian-type noise, with zero mean, and
hq.t/q.t
0
/iD2Dı.t t
0
/; (20.4)
hp.t/p.t
0
/iD2Qı.t t
0
/; (20.5)
hq.t/p.t
0
/iDhp.t/q.t
0
/iD
p
DQ
exp
jt t
0
j
! 2
p
DQı.t t
0
/ as ! 0; (20.6)

236 P. Z h u
where D and Q stand for the strength of additive and multiplicative noises,
respectively. The parameter measures the strength of correlations between q.t/
and p.t/. is the correlation time of the correlation between q.t/ and p.t/.When
the limit ! 0, the colored correlation becomes the white one. Employing the
Novikov theorem [35], Fox’s approach [36] and ansatz of Hanggi et al. [37], the
approximate Fokker–Planck equation (FPE) to (20.3)isgivenby[38–40]
@P .I ; t /
@t
D L
FP
P.I;t/; (20.7)
L
FP
D
@
@I
f.I/C
@
2
@I
2
G.I/; (20.8)
where
f.I/D2KI C
2F
1
I
1 C AI =F
1
C 2D C 2
D C 3b
0
I
1
2
C 2QI
; (20.9)
G(I) D 4
DI C 2b
0
I
3
2
C QI
2
; (20.10)
and
b
0
D
p
DQ
1 C 2K
1
K
F
1
: (20.11)
Note that this approximate Fokker–Plank equation holds under the condition
1C2K.1
K
F
1
/>0. Thus, when the system is operated above the thresh-
old (a
0
>0), there is no restriction on 0; when the system is operated at the
threshold (a
0
D 0), b
0
D
p
DQ,and(20.7) reduces to the case of the correlated
additive and multiplicative white noises; when the system is operated below the
threshold (a
0
<0), must satisfy 0 <.K C a
0
/=2Ka
0
.
In the case of a stationary state, the probability density function P
st
.I / of (20.7)
can be obtained below:
1. When a
0
>0, the probability density function is given by
P
st
.I / D N
QI C2b
0
I
1
2
C D
ˇ
1
A
F
1
I C 1
ˇ
2
exp
2
6
4
ˇ
3
arctan
QI
1
2
C b
0
q
DQ b
2
0
C ˇ
4
arctan
I
1
2
s
A
F
1
!
3
7
5
;
(20.12)
for jj1,where
ˇ
1
D
K
2Q
F
2
1
.AD F
1
Q/
2Œ.AD F
1
Q/
2
C 4b
2
0
F
1
A
1;
