Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay

Подождите немного. Документ загружается.

258 Y.-J. Zhao et al.

Fig. 21.5 EMD decomposition result of SR output

Figures 21.2 and 21.5 use the same original signal. In Fig. 21.2, we decompose

signal with EMD directly, for the reason of noise the ﬁrst IMF c

is mainly high-

frequency noise component. 30 Hz frequency component is decomposed into IMF

and is distorted. Ten hertz correspondence with c

 c

,forthelowam-

plitude it is hard to detect. Compared with Figs. 21.2 and 21.5, we can conclude

that SR C EMD method is better than only EMD method. For large signal the for-

mer performance is better than the latter and for weak signal only the former can

be detected and decomposed. Otherwise, SR C EMD method can reduce EMD de-

composition’s layer, as shown in ﬁgures, there are eight layers in Fig. 21.5 but only

six in Fig. 21.2.

21.5 Conclusion

In order to use EMD decomposition in weak signals under noisy background,

this paper puts forward a new method: using SR as pre-treatment and then per-

forming EMD decomposition. The experiment result proved that this method,

21 Empirical Mode Decomposition Based on Bistable Stochastic Resonance 259

compared with EMD directly, not only improve SNR, enhance weak signals, but

also improve the decomposition performance and reduce the decomposition layers

of signals.

Acknowledgments This work is supported by national 863 project fund Grant # 2007AA04Z414

and National Natural Science Foundation of China Grant # 50675153.

References

1. Huang NE, Shen Z, Long SR, et al (1998) The empirical mode decomposition and the

Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proc R Soc Lond

A 454:903–995

2. Huang NE (1996) Computer implicated empirical mode decomposition method, apparatus, and

article of manufacture [P]. U.S. Patent Pending

3. Deng Y (2001) Comment and modiﬁcation on EMD and Hilbert transform method [J]. Chinese

Sci Bull 46(3):257–263

4. Dai G-P, Liu B (2007) Instantaneous parameters extraction based on wavelet denoising and

EMD [J]. Acta Meteor Sin 28(2):158–162

5. Wang T, Wang Z, Xu Y (2005) Empirical mode decomposition and its engineering applications

based on SVD denoising [J]. J Vib Shock 24(4):96–98

6. Benzi R, Sutera A, Vulpiana A (1981) The mechanism of stochastic resonance. J Phys A

l4(11):L453–L4572

7. Leng Y-G, Wang T-Y, et al (2004) Power spectrum research of twice sampling stochastic reso-

nance response in a bistable system [J]. Acta Phys Sin 53:(3):717–723

8. Leng Y-G, Wang T-Y (2003) Numerical research of twice sampling stochastic resonance for the

detection of a weak signal submerged in a heavy noise [J]. Acta Phys Sin 52(10):2432–2437

9. Leng Y-G (2004) Mechanism analysis of the large signal scale-transformation stochastic reso-

nance and its engineering application study. Papers of PHD, Tianjin University, Tianjin

Chapter 22

Order Reduction of a Two-Span Rotor-Bearing

System Via the Predictor-Corrector

Galerkin Method

Deng-Qing Cao, Jin-Lin Wang, and Wen-Hu Huang

Abstract The predictor-corrector Galerkin method (PCGM) is employed to obtain

a lower order system for a two-span rotor-bearing system. First of all, a 32-DOF

nonlinear dynamic model is established for the system. Then, the predictor-corrector

algorithm based on the Galerkin method is employed to deal with the problem of

order reduction for such a complicated system. The ﬁrst six modes are chosen to

be the master subsystem and the following six modes are taken to be the slave sub-

system. Finally, the dynamical responses are numerically worked out for the master

and slave subsystems using the PCGM, and the results obtained are used to com-

pare with those obtained by using the SGM. It is shown that the PCGM provides a

considerable increase in accuracy for a little computational cost in comparison with

the SGM in which the ﬁrst six modes are reserved.

22.1 Introduction

Increasing demands for high performance rotating machinery have made the ro-

tor dynamic problems more and more complex, and more and more attention has

been drawn to the nonlinear dynamics of large-scale rotor-bearing systems. Usu-

ally, a large rotating machine consists of two or more shafts which are rigidly

or ﬂexibly coupled together to form a continuous rotor supported on three or

more hydrodynamic journal bearings. Such a rotating machine is referred to as

a multi-span rotor-bearing system. Up to now, research efforts on dynamics of

multi-span rotor-bearing systems are much fewer than those on single-shaft rotor

systems, e.g., the rigid or ﬂexible Jeffcott rotor. Ding and Krodkiewski [1]and

Krodkiewski et al. [2] proposed a general mathematical model of multi-bearing rotor

systems for the straightforward formulation of an approach for on-site identiﬁcation

D.-Q. Cao (



)

School of Astronautics, Harbin Institute of Technology, P.O. Box 137,

Harbin 150001, People’s Republic of China

e-mail: dqcao@hit.edu.cn

A.C.J. Luo (ed.), Dynamical Systems: Discontinuity, Stochasticity and Time-Delay,

DOI 10.1007/978-1-4419-5754-2

22,

 Springer Science+Business Media, LLC 2010

263

264 D.-Q. Cao et al.

of bearing alignment changes during system operation. Based on the approach

proposed in [1, 2], procedures for balancing large multi-bearing rotors have been

established in [3]. Hu et al. [4] designed a test rotor supported on four bearing to val-

idate that the vibration behaviors of statically indeterminate rotor-bearing systems

with hydrodynamic journal bearings are signiﬁcantly dependent on the relative lat-

eral alignment of bearing housing. The study of Ding and Leung [5] indicated that

the non-synchronous whirls of two ﬂexibly coupled shafts may affect each other. Fi-

nite element method (FEM) and computer simulation technology have been widely

used in designing and analyzing rotor-bearing systems. And in the machine struc-

ture analysis, a reﬁne discretization is usually necessary to obtain a reliable dynamic

model. In this process, a large set of second order differential equations of motion

for the multi-bearing system is established. Additionally, when one or more nonlin-

ear elements such as ﬂuid-bearing, ﬂuid seal, etc., are included in the system, which

is often case, the large order nonlinear systems are usually costly to solve in terms of

computer time and storage, especially over long-time intervals. Hence, it is essential

to reduce the order of the large-scale nonlinear dynamic system, and subsequently

to get a lower order dynamic system which is an approximate representative of the

original one.

The traditional order reduction methods, such as the Guyan order reduction

method [6] and standard Galerkin method (SGM) may also be applied to nonlin-

ear dynamic systems. Although the traditional order reduction methods proved to

be efﬁcient in constructing approximate solutions for nonlinear dynamic systems, it

has itself own limitation that accurate results may only be achieved through the in-

clusion of many modes in the reduced order system. If only a few nonlinear elements

exist, the large order system can be reduced using a ﬁxed-interface component mode

synthesis procedure (CMS) [7] in which the degrees of freedom (DOF) associated

with nonlinear elements are retained in the physical coordinates while the linear

subsystem, the DOF of which far exceeds the DOF of the nonlinear subsystem, are

truncated to a few dominant modes. However, if there are complex nonlinear terms

in the system, i.e., the DOF of the nonlinear subsystem is not small enough, the

practicability of ﬁxed-interface CMS is worth of further study.

An ideally order reduction method is sought to provide a reduced order model

that only contains a few modes. In pursuit of the goal, a large dynamical system

is transformed to modal coordinates and split into a master subsystem and a slave

subsystem. Then the nonlinear Galerkin method (NLGM) is developed, in which

a lower order subsystem is constructed by estimating and approximating the slave

subsystem as function of the master subsystem. The approximate relation between

the master subsystem and slave subsystem was given the name of approximate iner-

tial manifolds (AIM) [8–11]. One simple method for constructing the AIM has been

proposed in [11] by ignoring the time derivative term of the slave subsystem. The

AIM can be obtained by iteration. In particular, during numerically integrating the

reduced order system obtained via NLGM, constructing the AIM at each time step is

tedious and very costly. In order to avoid the disadvantage of the NLGM and at the

meantime to improve SGM, Garcia-Archilla et al. [12] proposed a so-called post-

processed Galerkin method (PPGM). The PPGM, which is as simple as the SGM

22 Order Reduction of a Two-Span Rotor-Bearing System 265

and has some advantage of NLGM, has been used to solve the nonlinear dynamics of

shells in [13] and the dissipative equation in ﬂuid dynamics under periodic boundary

conditions [14]. In the application of PPGM, the SGM is used and the AIM only

needs to be calculated when output is required. For the merit and fault of NLGM

and PPGM, we refer to the comments in [15, 16].

For the rotor-bearing system, since the oil ﬁlm forces are nonlinear functions

of the displacements, the velocities at bearings and the rotating speed of the ro-

tor, the NLGM may be not available due to the limitation on the displacements at

bearings. In fact, by ignoring the time derivative term of the slave subsystem to get

the AIM may overtop the limitation on the displacements. In order to get an or-

der reduction of a large-scale rotor-bearing system, the predictor-corrector Galerkin

method (PCGM) has been proposed in [17] based on the ideals of NLGM and

PPGM. In [17], a large nonlinear dynamical system is split into a master subsystem,

a slave subsystem, and a negligible subsystem. In a general way, the lower modes

whose frequencies are close to the frequencies of external periodic excitations dom-

inate the dynamic behaviors of the large dynamical system, and the corresponding

modes can be chosen to be the so-called master subsystem. In order to save the cal-

culating time, the order of the slave subsystem may be chosen to be the same as the

master subsystem, while the order of the negligible subsystem may far exceed the

order of master subsystem.

A 32-DOF nonlinear dynamic model is established for a two-span rotor-bearing

system in this paper. The predictor-corrector algorithm based on the Galerkin

method is employed to deal with the problem of order reduction for such a com-

plicated system. The ﬁrst six modes are chosen to be the master subsystem and the

following six modes are taken to be the slave subsystem. The dynamical responses

are numerically worked out for the master and slave subsystems using the PCGM,

and the results obtained are used to compare with those obtained by using the SGM.

It is shown that the PCGM provides a considerable increase in accuracy for a little

computational cost in comparison with the SGM.

22.2 Modeling of the Two-Span Rotor-Bearing System

Consider a two-span rotor-bearing system as shown in Fig. 22.1. It consists of four

disks and two shafts, which are rigidly coupled together via a coupling. The shaft

is treated as a free-free body and is modeled by FEM based on Euler beam theory.

Each node has four degrees of freedom. On the free-free rotor, all external forces can

be applied, no matter whether they are linear or nonlinear, static or time-dependent.

The dynamic responses of the two-span rotor-bearing system are governed by the

following differential equations of motion.

M Rz C DPz C Kz D f.z; Pz;t/ D f

.z; Pz/ C f

.t/ C g; (22.1)

where M; C; K 2 R

3232

are the mass, damping, and stiffness matrices, and

.z; Pz/; f

.t/; g 2 R

are the nonlinear ﬂuid ﬁlm force, unbalance force, and

266 D.-Q. Cao et al.

Fig. 22.1 The sketch of the two-span rotor-bearing system

gravitational force vectors, respectively. The short bearing model [18]isemployed

to describe the ﬂuid ﬁlm forces at four bearings. The displacement vector is

z D Œx

; ˇ

;

; ˇ

;

;:::;x

; ˇ

;



2 R

;

where r is the number of nodes, x

,andˇ

;

are the lateral displacements

and rotation angles of the ith nodal point along the horizontal and vertical direction,

respectively. The m

.s D 1; 2; 3; 4/ is the mass of the sth disk, e

is the eccentricity

of the sth disk, and J

is the transverse moment of inertia of the sth disk as shown

in Fig. 22.1.

22.3 The Predictor-Corrector Galerkin Method

The original system described by (22.1) can be split into three parts by the modes

of the linearized part of (22.1), i.e., a master subsystem, a slave subsystem, and a

negligible subsystem. To do this, the solution z isassumedtobeintheform

z D „ D ˆ

 C ‰

C Z

; (22.2)

where DŒ; ;

;„DŒˆ

;‰

; Z

;ˆ

DŒ'

;:::;'

;‰

DŒ'

mC1

;:::;'

mCs

;

D Œ'

mCsC1

;:::;'

mCsCp

,and'

s are the eigenmodes of the linearized part of

(22.1). Substituting (22.2)into(22.1) and multiplying with „

from the left, (22.1)

can be written as

 C C

 C K D f.„;„

;t/; (22.3)

where

M;C and K are the diagonal matrices in which the diagonal elements

respectively are

D '

; c

D '

and k

D '

; (22.4)

and the generalized force is

D '

f.„;„

;t/ for i D 1;2;:::n.

22 Order Reduction of a Two-Span Rotor-Bearing System 267

The matrices M; C; K and the force vector f are rearranged in the form.

M D

;

C D

;

K D

;

f D

Then, (22.3) can be rewritten as

C

 D f

.ˆ

C‰

; ˆ

C‰

;t/; (

22.5a)

D f

.ˆ

C‰

; ˆ

C‰

;t/; (

22.5b)

 C

 D f

.ˆ

C‰

; ˆ

C‰

;t/: (

22.5c)

The excitation frequency of the rotor is far from the higher modes, the contribution

of higher modes is considered to be insigniﬁcant. Thus, by neglecting (22.5c)or

setting  D 0, the entire system is approximated by

 C

 D f

.ˆ

 C ‰

;ˆ

 C ‰

;t/; (22.6a)

D f

.ˆ

 C ‰

;ˆ

 C ‰

;t/: (22.6b)

In the process of numerical integration of the system, the reﬁned calculation of the

master subsystem is necessary. Equation (22.6b) correspondsto the slave subsystem,

for which the solution could be approximately carried out. Therefore, the time step

T for (22.6b) may be chosen as several times as the time step t for (22.6a). The

solving procedures of the PCGM proposed in [17] can be described as

1. Set T D k  t (k>1is an integer). .t/;

.t/ and .t/;

.t/ are assumed

to be known at a given time t.D mT D mkt for an integer m).

2. To calculate the force vector at time t,

(

.ˆ

.t/ C‰

.t/; ˆ

.t/ C‰

.t/; t/

.ˆ

.t/ C ‰

.t/; ˆ

.t/ C ‰

.t/; t/

3. The dynamic responses .t C T / and

.t C T / of the slave subsystem are

predicted by (22.6b) at time t C T . Then, the dynamic response of the slave

subsystem at time t C j t are given by the interpolation method as

.t C j  t/ D .t/ C

j  Œ .t C T /  .t /

;

.t C j  t/ D

.t/ C

j 



.t C T / 

.t/



;

for j D 1;:::;k  1:

268 D.-Q. Cao et al.

4. The dynamic responses .t Cj t/ and .t Cj t/ of the master subsystem

are solved by integration of (22.6a) at time t C j  t.Whenj D 1, the force

vector

has been obtained from the second step; when j>1, the force vector

.ˆ

.t C .j 1/  t/ C ‰

.t C .j  1/  t/;

.t C .j  1/  t/ C ‰

.t C .j  1/  t/; t C .j  1/  t/;

where .t C.j 1/ t/ and

.t C.j 1/ t/ are given from the third step.

Up to t C T , the dynamic responses .t C k  t/ and

.t C k  t/ of the

master subsystem are obtained, i.e., .t C T / and

.t C T /.

5. To repeat the processes from Step 2 to Step 5, we can get the solution of the

system for next time step T .

22.4 Numerical Results and Discussion

A two-span rotor-bearing model with speciﬁc material constants and structural pa-

rameters listed in Table 22.1 is now presented to explore the complicated nonlinear

dynamic behavior of the system. Numerical calculations based on the procedures of

PCGM are carried out. The ﬁrst six modes are kept as the master subsystem; the

Table 22.1 The geometrical and physical parameters for

the rotor-bearing system

Physical properties Value

D L

=2 D L

=3 0.38267 m

0.25 m

D L

=2 D L

=3 0.414 m

D m

50.31 kg

45.32 kg

31.63 kg

D J

0:514 kg m

0:416 kg m

0:203 kg m

D e

3  10

5

4  10

5

Journal and shaft radius 0.057 m

Bearing length 0.03 m

Radial clearance 0:2 10

3

Dynamic viscosity 0.018 Pa s

Mass density 7; 850 kg=m

Young’s modulus 2:06 10

N=m

Number of elements 7

Number of node (r)8

22 Order Reduction of a Two-Span Rotor-Bearing System 269

slave subsystem consists of the following six modes and the remained modes are

neglected during numerical integration. At the meantime, the SGM with the ﬁrst

six modes is also selected to reduce the number of DOF. We should note that the

contribution of the slave subsystem is neglected in the integration of SGM.

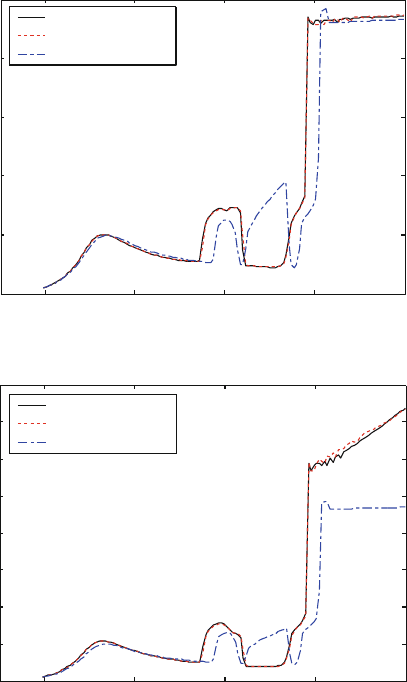
The frequency-response curves of displacements at the ﬁrst bearing and the

ﬁrst disk from the left are shown in Fig. 22.2a, b, respectively. It can be ob-

served from Fig. 22.2 that the dynamical responses of the original system and

the PCGM-based reduced system are nearly indistinguishable, whereas the SGM-

based reduced system exhibits an appreciable error after 4,740 rpm (after ﬁrst order

critical speed), especially the frequency-response curves at the disk as shown in

0 1000 3000 5000 7000 9000

0.2

0.4

0.6

0.8

Rotational speed [rpm]

Amplitude, x

Original System

PCGM (6+6)

SGM (6-DOF)

0 1000 3000 5000 7000 9000

0.2

0.4

0.6

0.8

1.2

1.4

1.6

Rotational speed[rpm]

Original System

PCGM (6+6)

SGM (6-DOF)

Fig. 22.2 Comparison of frequency–response curves using different methods: (a) left bearing;

(b) the ﬁrst disk from the left

270 D.-Q. Cao et al.

0 1000 3000 5000 7000 9000

Rotational speed [rpm]

0 1000 3000 5000 7000 9000

Rotational speed [rpm]

−

0.5

−

0.5

−1

−0.5

0.5

Fig. 22.3 Comparison of bifurcation diagrams for different order reduction methods: (a)the

original system; (b)thePCGM;(c)theSGM

Fig. 22.2b. The ﬁrst jump phenomenon appears at the rotating speed 4,440 rpm

on the frequency-response curves of both original system and reduced order sys-

tem obtained through PCGM. The jump phenomenon in the reduced order system