Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay
Подождите немного. Документ загружается.

22 Order Reduction of a Two-Span Rotor-Bearing System 271
0
1000
3000
5000
7000
9000
1000
3000
5000
7000
9000
0
0.5
1
Frequ
ency[rpm]
Frequency[rpm]
Frequency[r/min]
Response
0
1000
3000
5000
7000
9000
1000
3000
5000
7000
9000
0
0.5
1
Response
0
1000
3000
5000
7000
9000
1000
3000
5000
7000
9000
0
0.5
1
Response
Rotational speed[rpm]
Rotational speed[rpm]
Rotational speed[r/min]
a
b
c
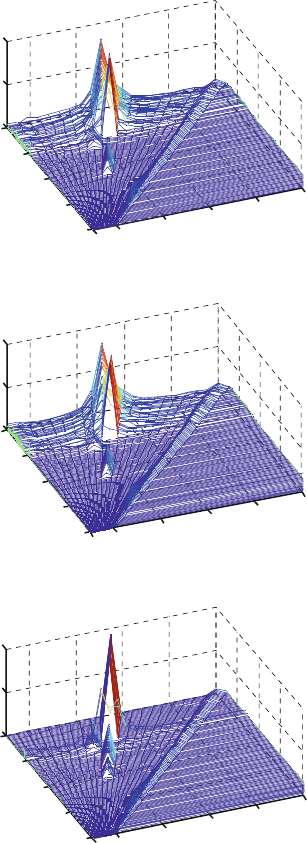
Fig. 22.4 Comparison of three-dimensional spectrum plots for different order reduction methods:
(a) the original system; (b)thePCGM;(c)theSGM
obtained by the SGM is delayed near 300 rpm. Observing Figs. 22.2 and 22.3
we find that a period-doubling bifurcation (Fig. 22.3a–c) results in a transition
from synchronous whirl to non-synchronous whirl with whirling frequency being
equal to half of rotating speed (Fig. 22.4a–c), when the fist jump phenomenon
272 D.-Q. Cao et al.
take place. In the original system, with the increases of the rotating speed, the
synchronous motion again occurs in the speed range 5,460–6,240rpm, after rotating
speed 6,240 rpm more complex nonlinear dynamic behaviors begin evolvement as
shown in Figs. 22.3aand22.4a. It is delightful that the dynamic phenomena of re-
duced order system obtained via the PCGM are coincident with those of the original
system (Figs. 22.3band22.4b). However, the reduced order system obtained via the
SGM can not reproduce the actual nonlinear dynamic phenomena of original system
(Figs. 22.3cand22.4c) after the fist bifurcation point in the original system. In order
to achieve the accurate results, more modes should be included for the SGM.
22.5 Conclusions
A 32-DOF nonlinear dynamic model has been established for the two-span rotor-
bearing system. A lower order subsystem with 6-DOF has been taken as the master
subsystem. The master subsystem associated with the slave subsystem which also
has 6-DOF has been numerically solved using the predictor-corrector Galerkin
method proposed in [17]. It has been shown that the PCGM provided a considerable
increase in accuracy for a little computational cost in comparison with the SGM in
which the first six modes were reserved. The numerical results indicated that the in-
fluence of some higher modes should be taken into account. The PCGM can achieve
the request accuracy and reduce the order of the large-scale nonlinear dynamical
system without losing essential dynamical behaviors of the original system.
Acknowledgments This research was supported by National Natural Science Foundation
of China (10772056, 10632040) and the Natural Science Foundation of Hei-Long-Jiang Province,
China (ZJG0704).
References
1. Ding J, Krodkiewski JM (1993) Inclusion of static indetermination in the mathematical model
for non-linear dynamic analyses of multi-bearing rotor systems. J Sound Vib 164(2):267–280
2. Krodkiewski JM, Ding J, Zhang N (1994) Identification of unbalance change using a non-linear
mathematical model for multi-bearing rotor systems. J Sound Vib 169(5):685–698
3. Ding J (1997) Computation of multi-plane imbalance for a multi-bearing rotor system. J Sound
Vib 205(3):364–371
4. Hu W, Miah H, Feng NS, et al (2000) A rig for testing lateral misalignment effects in a flexible
rotor supported on three or more hydrodynamic journal bearings. Tribol Int 33:197–204
5. Ding Q, Leung AYT (2005) Numerical and experimental investigations on flexible multi-
bearing rotor dynamics. J Vib Acoust 127:408–415
6. Guyan RJ (1965) Reduction of stiffness and mass matrices. AAIA J 3(2):380
7. Sundararajan P, Noah ST (1998) An algorithm for response and stability of large order non-
linear systems-application to rotor systems. J Sound Vib 214(4):695–723
8. Devulder C, Marion M (1992) A class of numerical algorithms for large time integration: the
nonlinear Galerkin method. SIAM J Numer Anal 29(2):462–483
22 Order Reduction of a Two-Span Rotor-Bearing System 273
9. Foias C, Manley O, Temam R (1993) Iterated approximate inertial manifolds for Navier–Stokes
equations in 2-D. J Math Anal Appl 178:567–583
10. Sthindl A, Troger H (2001) Methods for dimension reduction and their application in nonlinear
dynamics. Int J Solids Struct 38:2131–2147
11. Titi ES (1990) On approximate inertial manifolds to the Navier–Stokes equations. J Math Anal
Appl 149:540–570
12. Garcia-Archilla B, Novo J, Titi ES (1998) Postprocessing the Galerkin method: a novel ap-
proach, to approximate inertial manifolds. SIAM J Numer Anal 35:941–972
13. Sansour C, Wriggers P, Sansour J (2003) A finite element post-processed Galerkin method
for dimensional reduction in the non-linear dynamics of solids: applications to shells. Comput
Mech 32:104–114
14. Garcia-Archilla B, Novo J, Titi ES (1999) An approximate inertial manifolds approach to post-
processing the Galerkin method for the Navier–Stokes equations. Math Comput 68:893–911
15. Rega G, Troger H (2005) Dimension reduction of dynamical systems: methods, models, appli-
cations. Nonlinear Dyn 41:1–15
16. Matthies HG, Meyer M (2003) Nonlinear Galerkin methods for the model reduction of nonlin-
ear dynamical systems. Comput Struct 81:1277–1286
17. Cao DQ, Wang JL, Huang WH (2010) The predictor-corrector Galerkin method and its appli-
cation in a large-scale rotor-bearing system. J Vib Shock 29(2):100–105
18. Adiletta G, Guido AR, Rossi C (1996) Chaotic motions of a rigid rotor in short journal bear-
ings. Nonlinear Dyn 10:251–269

Chapter 23
Stiffness Nonlinearity Classification
Using Morlet Wavelets
Rajkumar Porwal and Nalinaksh S. Vyas
Abstract A methodology based on wavelet transform using standard and
low-oscillation Morlet wavelets is presented to distinguish between symmetric and
asymmetric polynomial form of stiffness nonlinearities. Free vibration response
of the system is wavelet transformed and ridges are estimated. Characteristics of
ridges in conjunction with analytical solutions from Krylov–Bogoliubov method
are used to classify the nonlinearities. Numerical simulations are performed on the
quadratic and mixed parity nonlinear oscillator to illustrate the procedure.
23.1 Introduction
Presence of many forms of the nonlinearities in the restoring force and dissipa-
tive forces makes identification and parameter estimation of nonlinear systems
quite involved. Classification and identification of nonlinearities is one of the
important aspects of system parameter estimations. A brief description of vari-
ous identification schemes can be found in Kerschen et al. [4] and Worden and
Tomlinson [14].
Wavelet transform technique for nonlinear system identification is being used
more frequently [4, 10]. The capability of wavelet transform to capture instanta-
neous frequency and amplitude envelope makes it suitable for the identification of
nonlinear systems. Transient vibration of a weakly nonlinear system can be mod-
eled as a signal whose amplitude envelope and instantaneous frequency change
with time. Closed form solutions obtained from Krylov–Bogoliubov technique es-
tablish the relationships for amplitude envelope and instantaneous frequency for a
weakly nonlinear system [9]. Instantaneous frequency and amplitude envelope of
the given signal can also be determined numerically using the wavelet transform.
R. Porwal (
)
Department of Mechanical Engineering
Shri G. S. Institute of Technology and Science, 23 Park Road, Indore 452003, India
e-mail: rkporwal@iitk.ac.in; rajkumarporwal@hotmail.com
A.C.J. Luo (ed.), Dynamical Systems: Discontinuity, Stochasticity and Time-Delay,
DOI 10.1007/978-1-4419-5754-2
23,
c
Springer Science+Business Media, LLC 2010
275

276 R. Porwal and N.S. Vyas
The numerical results obtained from wavelet transform and closed form solutions
from Krylov–Bogoliubov technique are used in conjunction to determine the system
parameters.
Staszewski [12] applied the analytic wavelet transform techniques to nonlinear
systems of the Duffing type. Lardies and Ta [5] analyzed the system containing non-
linear damping. In another paper, Ta and Lardies [13] addressed the systems having
polynomial type of nonlinearity on damping and stiffness. They demonstrated the
application of the procedure on the systems with symmetric polynomial type of
stiffness nonlinearities.
Most parameter estimation procedures are based on an inherent assumption about
the form of nonlinearities. However, for complex engineering systems, it is dif-
ficult to recognize the actual form of nonlinearities. A third degree polynomial
form of stiffness is considered in the present study and a methodology based on
wavelet transform using standard and low-oscillation Morlet wavelets is suggested
to distinguish between the symmetric and asymmetric polynomial forms of stiffness
nonlinearity.
23.2 Response of the Nonlinear System
For weakly nonlinear systems given by
Ry C y D "F .y; Py/I (23.1)
the response through the Krylov–Bogoliubov method is represented as
y D A./ cos ΠC ./ ; (23.2)
where A./ and ./ are calculated by [8].
P
A D
"
2
Z
2
0
F.Acos ; A sin /sin d ; (23.3)
P
D
"
2A
Z
2
0
F.Acos ; A sin /cos d : (23.4)
The instantaneous frequency Œ!./ of the response signal is time derivative of the
phase i.e., Œ1 C
P
./.
A damped single degree of freedom system with nonlinear stiffness modeled by
a polynomial of degree three, executing free vibration, initiated by providing some
initial displacement, can be modeled as
Ry C 2 Py C y C "
2
y
2
C "
3
y
3
D 0; y.0/ D 1; Py.0/ D 0: (23.5)

23 Stiffness Nonlinearity Classification Using Morlet Wavelets 277
In absence of quadratic term, the response of the system is given by [8]
y./ D A
0
e
cos
C
Z
0
3
8
"
3
A
2
./d C
0
: (23.6)
Here constants A
0
and
0
depend on the initial conditions. Amplitude envelope
A./ and instantaneous frequency !./ are given by the following expressions
A./ D A
0
e
; (23.7)
!./ D 1 C
3
8
"
3
A
2
./: (23.8)
The above relationship involves dependence of the frequency of oscillations on the
amplitude of oscillations.
Presence of quadratic term makes the problem little involved. The Krylov–
Bogoliubov method, which is first order averaging technique is not able to incor-
porate the effect of quadratic nonlinearity [8]. In order to use Krylov–Bogoliubov
method and to have a better representation of response for quadratic and mixed-
parity nonlinear oscillators, Porwal and Vyas [11] analyzed the positive displace-
ment and negative displacement motion separately.
Motion during positive half cycle is governed by
Ry C 2 Py C y C "
2
y
j
y
j
C "
3
y
3
D 0; for y>0 (23.9)
Response during the ith positive half cycle is given by
y
pi
./ D A
pi
e
cos
!
pi
C
pi
; (23.10)
where
!
pi
D
1 C
4"
2
Y
pi
3
C
3"
3
Y
2
pi
8
!
; (23.11)
A
pi
and
pi
are constants which depend on the conditions at the beginning of the
half cycle. Y
pi
is the amplitude of oscillation and !
pi
is the average frequency of
oscillation. Governing equation of motion during negative half cycle is
Ry C 2 Py C y "
2
y
j
y
j
C "
3
y
3
D 0; for y<0: (23.12)
Response during the jth negative half cycle is given by
y
nj
./ D A
nj
e
cos
!
nj
C
nj
; (23.13)
278 R. Porwal and N.S. Vyas
where
!
nj
D
1
4"
2
Y
nj
3
C
3"
3
Y
2
nj
8
!
; (23.14)
Constants A
nj
and
nj
depend on the conditions at the beginning of half cycle. Y
nj
is
the amplitude of oscillation and !
nj
is the average frequency of oscillation. A semi
analytical approach to determine all these quantities for the complete motion is de-
scribed by Porwal and Vyas [11]. The frequency changes from half cycle to half
cycle as per the above equations, (23.11)and(23.14). Wavelet transform is used to
detect and characterize the system using this fact.
23.3 Wavelet Transform
The continuous wavelet transform (CWT) for a finite energy signal y./ using ad-
missible wavelet function g./ is defined by the integral [3]
W
y
.a; b/D
h
y; g.; a; b/
i
D
1
p
a
Z
1
1
y./g
b
a
dt; where y./ 2 L
2
.R/
(23.15)
g
b
a
is complex conjugate of g
b
a
. Variables a and b are scale and
translational parameters, respectively. The above mentioned definition of wavelet
transform i.e., (23.15) can be converted to the frequency domain using Parseval
identity [3]
W
y
.a; b/ D
p
a
2
Z
1
1
Y.!/G.a!/e
j!b
d!: (23.16)
Here Y.!/ is the Fourier transform of y./ and G.!/ is the Fourier trans-
form of g./. The bar over G.a!/ i.e.,
N
G.a!/ denotes complex conjugate of
G.a!/. This result can be interpreted as an inverse Fourier transform of the
function
p
aY .!/ G.a!/. Equation (23.16) is used here for computation in or-
der to take advantage of an efficient Fast Fourier Transform (FFT) algorithm.
23.3.1 Wavelet Transform of the Response Signal
The system response represented by (23.6), or (23.10)and(23.13) can be written in
general as
y./ D A./ cosŒ./ ; where
P
./ D !./: (23.17)
23 Stiffness Nonlinearity Classification Using Morlet Wavelets 279
Under the assumption of small damping, the response signal can be considered as
an asymptotic signal if oscillation due to the phase term ./ is more significant
than that coming from the amplitude term A. / [2]. A reasonable approximation of
wavelet transform of an asymptotic signal (23.17) turns out to be [2,6]
W
y
.a; b/ D
p
a
2
A.b/e
j.b/
N
G.a!/: (23.18)
23.3.1.1 Standard Morlet Wavelet
Standard Morlet wavelet function with central frequency !
0
is given by
g./ D
1
./
1=4
e
2
=2
e
j!
0
: (23.19)
Its Fourier transform is
G.!/ D .4/
1=4
e
.!!
0
/
2
=2
: (23.20)
!
0
D 5 is used here to meet the admissibility criterion [2]. Therefore, a reasonable
approximation of wavelet transform of an asymptotic signal (23.17)is
W
y
.a; b/ D
p
a
2
A.b/e
j.b/
.4/
1=4
e
.a!!
0
/
2
=2
: (23.21)
The result of wavelet transform is presented as a 2D plot of normalized scalogram
ˇ
ˇ
W
y
.a; b/
ˇ
ˇ
2
=a
. The magnitude of normalized scalogram is represented by pro-
portional intensity on the plot as a function of .a; b/. Ridge of the wavelet transform
is defined to extract useful information out of the spread normalized scalogram.
Wavelet ridge is closely related to instantaneous frequency of the signal. A ridge
is defined as the locus in time–frequency plane along which normalized scalogram
attains the maxima; mathematically
@
@a
ˇ
ˇ
W
y
.a; b/
ˇ
ˇ
2
a
!
D 0: (23.22)
Substituting the transform (23.21)into(23.22) and simplification gives the locus of
the ridge as
a
r
.b/ D
!
0
!.b/
; (23.23)
where a
r
.b/ is the scale along the ridge. In order to determine the scale corre-
sponding to ridge a
r
.b/ the maxima of normalized scalogram is noted for each
280 R. Porwal and N.S. Vyas
time location b in the time–frequency representation calculated by (23.16)andthe
corresponding scale is obtained. Subsequently, the instantaneous frequency !.b/ at
a particular time can be determined.
23.3.1.2 Complete Morlet Wavelet
Time resolution of standard Morlet wavelet depends on !
0
(Table 23.1) whose
value is kept greater than 5 for the mean of wavelet function to approach zero, a
condition to fulfill admissibility requirement. It is therefore, unable to capture any
phenomenon which is more temporal in nature.
In order to increase time resolution and capture the temporal phenomenon, use of
complete Morlet wavelet has been suggested. This allows us to use lower value of
central frequency !
0
. Since the central frequency is lower than the standard Morlet
wavelet, it is known as low-oscillation Morlet wavelet. !
0
D 1 is used in the present
work to have better time resolution . Initially low oscillation Morlet wavelet was
used as a pattern matching tool to detect and classify P waves in ECG signal by
Michaelis [7]. Later Addison et al. [1] lucidly explained the underlying mathematics
and applied it to sonic echo NDT signal used for the analysis of structure elements.
The complete Morlet wavelet is defined as follows
g.t/ D
1
./
1=4
e
j!
0
e
!
2
0
2
e
2
=2
: (23.24)
Its Fourier transform is
G.!/ D .4/
1=4
e
.
!
2
C!
2
0
/
=2
.e
!!
0
1/ : (23.25)
With complete Morlet wavelet, the wavelet transform of an asymptotic signal
(23.17) can be written approximately as [6]
W
y
.a; b/ D
p
a
2
A.b/e
j.b/
.4/
1=4
e
.
a!
2
C!
2
0
/
=2
.e
a!!
0
1/ : (23.26)
The wavelet ridge is obtained by employing the expression (23.22), thus
a
r
D
1
!
0
!
log
a
r
!
a
r
! !
0
: (23.27)
Table 23.1 Properties of standard Morlet wavelet functions
Time center Frequency center Time spread Frequency spread
b
!
o
a
!
0
!
1
p
2
!
!
0
1
p
2
23 Stiffness Nonlinearity Classification Using Morlet Wavelets 281
Equation (23.27) is solved numerically for instantaneous frequency (!)after
determining locus of ridge (a
r
) from the maxima of normalized scalogram at
each time instant.
23.4 Illustration
Following three representative cases are numerically simulated:
1. "
2
and "
3
are present i.e., asymmetric mixed parity oscillator.
2. "
2
is present and "
3
is 0 i.e., asymmetric quadratic oscillator.
3. "
2
is 0 and "
3
is present i.e., symmetric cubic oscillator.
The steps involved in classifying the system using ridges of wavelet transform are
shown schematically in Fig. 23.1 for a mixed parity nonlinear oscillator in which
both "
2
and "
3
are eqal to 0:1 i.e., case (1). Damping factor D 0:01 is as-
sumed in all the simulations. Figure 23.1a is a simulated response of the system
obtained through Runge–Kutta method. Results in Fig. 23.1b–d are obtained using
standard Morlet wavelet while the results in Fig.
˙
23.1e–g are obtained using low os-
cillation Morlet wavelet. Wavelet transform of the response is shown in Fig. 23.1b.
Ridge obtained over the relevant scale is shown in Fig.23.1c. Locus of ridge is con-
verted to variation of instantaneous frequency with time in Fig. 23.1d. The trend of
the graph shows that the frequency decreases continuously as the amplitude of os-
cillation decreases. The corresponding results in Figs. 23.1e–g indicate that the low
oscillation Morlet wavelet is able to capture the change in instantaneous frequency
form half cycle to half cycle. The instantaneous frequency shows oscillating behav-
ior due to the different governing law during positive and negative motion and this
fact is also evident from (23.11) and (23.14).
The results obtained for the other two cases are shown in Fig. 23.2. Figure 23.2a–c
belongs to case (2). Figure 23.2a shows the response of the system for "
2
D 0:1
and "
3
D 0. Instantaneous frequencies obtained using standard Morlet wavelet and
low oscillation Morlet wavelet are shown in Fig. 23.2b, c, respectively. Here the
two wavelets yield different loci for the instantaneous frequency. In absence of "
3
,
the frequency locus obtained by the standard Morlet wavelet remains in the close
vicinity of unity. The low-oscillation Morlet wavelet yields an oscillatory frequency
plot.
Figure 23.2d–f belongs to case (3) and shows the results for "
2
D0 and "
3
D0:1.
Results obtained are same for both wavelets since the instantaneous frequency
changes smoothly with the amplitude of oscillation as given by (23.8).
