Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay

Подождите немного. Документ загружается.

282 R. Porwal and N.S. Vyas

0 20 40 60 80

y( τ)

0 20 40 60 80

30 40 50 60 70

4.8

5.2

30 40 50 60 70

0.96

0.98

1.02

1.04

ω(τ)

0 20 40 60 80

30 40 50 60 70

1.3

1.35

1.4

30 40 50 60 70

0.96

0.98

1.02

1.04

−1

−0.5

0.5

1.5

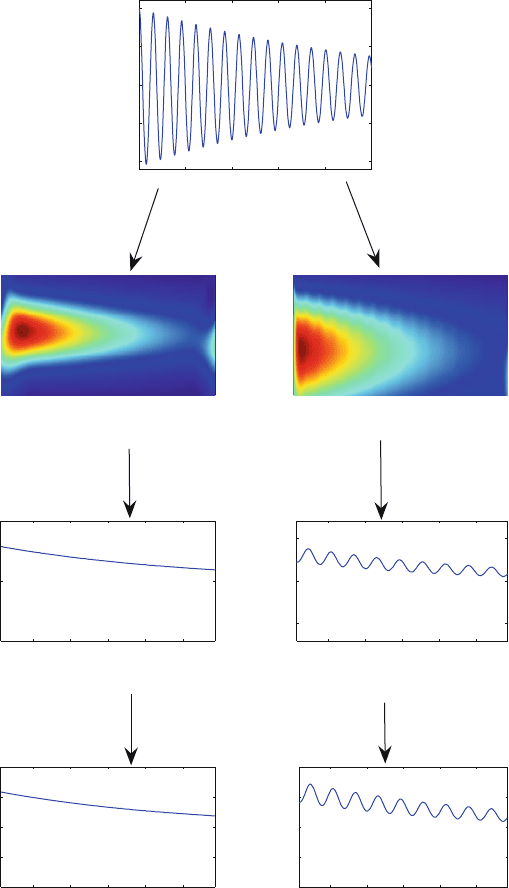
Fig. 23.1 (a) Response of a mixed-parity nonlinear oscillator "

D 0:1 and "

D 0:1 (b) Wavelet

transform of the response using standard Morlet wavelet (c) Ridge of the wavelet transform (d)In-

stantaneous frequency of the response (e) Wavelet transform of the response using low-oscillation

Morlet wavelet (f) Ridge of the wavelet transform (g) Instantaneous frequency of the response

23 Stiffness Nonlinearity Classiﬁcation Using Morlet Wavelets 283

30 40 50 60 70

y(τ)

30 40 50 60 70

ω(τ)

0.96

0.98

1.02

1.04

0.96

0.98

1.02

1.04

−1

=0.1,

y(τ)

ω(τ)ω(τ)

30 40 50 60 70

−1

30 40 50 60 70

0.96

0.98

1.02

1.04

30 40 50 60 70

0.96

0.98

1.02

1.04

=0,

=0.1

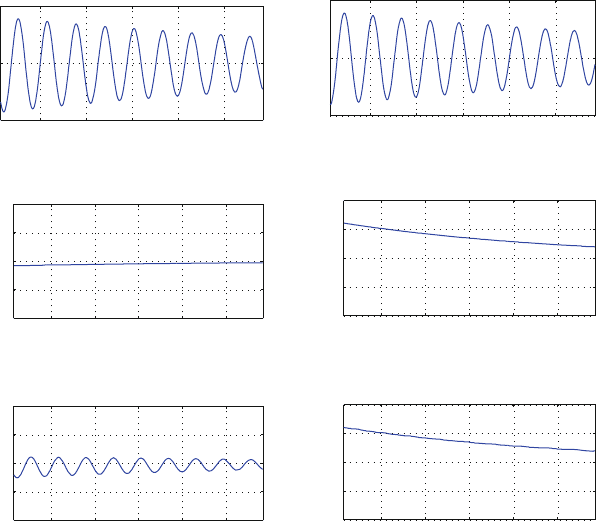
Fig. 23.2 (a) Simulated response for case 2 (b) Instantaneous frequency using standard Morlet

wavelet for case 2 (c) Instantaneous frequency using low-oscillation Morlet wavelet for case 2

(d) Simulated response for case 3 (e) Instantaneous frequency using standard Morlet wavelet for

case 3 (f) Instantaneous frequency using low-oscillation Morlet wavelet for case 3

23.5 Conclusions

The frequency loci obtained through standard Morlet wavelet are non-oscillatory.

Locus of frequency in this case is better explained by considering corresponding

symmetric case i.e., the (23.8). Standard Morlet wavelet averages out the effect

of asymmetric nonlinearity over a number of response cycles due to its higher

time spread. This averaged out results are used to ﬁnd the presence of "

.Low-

oscillation Morlet wavelet, due to its ability to capture the temporal phenomenon,

is able to distinguish between the symmetric and asymmetric forms easily. It gives

non-oscillatory frequency locus for symmetric nonlinearity while for asymmetric

nonlinearity the frequency locus is oscillatory. The oscillatory locus of frequency is

better explained by the (23.11) and (23.14).

284 R. Porwal and N.S. Vyas

References

1. Addison PS, Watson JN, Feng T (2002) Low-oscillation complex wavelets. J Sound Vib

254(4):733–762

2. Carmona R, Hwang W, Torresani B (1998) Wavelet analysis and its application: practical time

frequency analysis, vol 9. Academic, San Diego, CA

3. Chui CK (1992) An introduction to wavelets. Academic, San Diego, CA

4. Kerschen G, Worden K, Vakakis AF, Golinval JC (2006) Past, present and future of nonlinear

system identiﬁcation in structural dynamics. Mech Syst Signal Process 20:505–592

5. Lardies J, Ta MN (2005) A wavelet based approach for the identiﬁcation of damping in non-

linear oscillator. Int J Mech Sci 47:1262–1281

6. Mallat S (1998) A wavelet tour of signal processing. Academic, San Diego, CA

7. Michaelis M, Penz S, Black C, Sommer G (1993) Detection and classiﬁcation of p waves using

gabor wavelets. In: Computers in cardiology 1993. Proceedings of IEEE, pp 531–534

8. Mickens RE (1995) Oscillations in planar dynamic systems. World Scientiﬁc Publishing,

Singapore

9. Nayfeh AH (1973) Perturbation methods. Wiley, New York

10. Peng Z, Chu F (2004) Application of the wavelet transform in machine condition monitoring

and fault diagnostics: a review with bibliography. Mecha Syst Signal Process 18:199–221

11. Porwal R, Vyas NS (2008) Damped quadratic and mixed-parity oscillator response using

Krylov–bogoliubov method and energy balance. J Sound Vib 309:877–886

12. Staszewski W (1998) Identiﬁcation of non-linear systems using multi-scale ridges and skele-

tons of the wavelet transform. J Sound Vib 214(4), 639–658

13. Ta MN, Lardies J (2006) Identiﬁcation of weak nonlinearities on damping and stiffness by the

continuous wavelet transform. J Sound Vib 293:16–37

14. Worden K, Tomlinson G (2001) Nonlinearity in structural dynamics: Detection, identiﬁcation

and modelling. Institute of Physics Publishing, Bristol, Avov and Philadelphia, PA

Chapter 24

Dynamics of Wire-Driven Machine Mechanisms:

Literature Review

Timo Karvinen and Erno Keskinen

Abstract The state-of-the art of the mechanical properties of wire ropes and the

dynamics simulation of wire rope mechanisms is reviewed in this paper. A special

emphasis is put on the tension dependent Young’s modulus and the damping of the

wire rope in the part dealing with the mechanical properties. In the part discussing

the dynamics simulation, the simpliﬁcation of the complex system and the connec-

tion between the rope and the pulley are accentuated. There is plenty of literature on

modeling the material properties and they can be predicted accurately. There is still

room for new developments in the dynamics simulation of wire rope systems.

24.1 Introduction

During the past two decades or so, considerable interest has been shown in the me-

chanical characteristics of helically wound steel cables for use in both onshore and

offshore applications such as bridges, oil drilling platforms, cranes, and elevators.

Most wire ropes are constructed from either a single strand or from several strands

that are wound around a core. This core may be a strand in itself or it may be a

ﬁbrous or deformable element. The strand is constructed of wires that are wound

around a central wire. The design of wire rope cross-sections dates back to the late

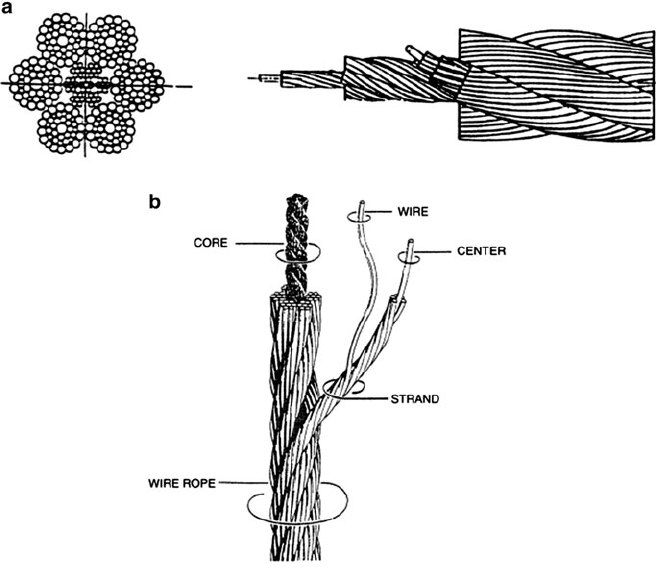
1800s and has been continuously improved ever since. A typical wire rope is shown

in Fig. 24.1. Several modeling approaches are based on the nonlinear equations of

equilibrium of a thin helical rod [2] and consider the torsion and bending stiffness of

the wires. The theory of wire ropes is presented very extensively in the book of [3].

The parameters affecting the wire rope properties are:

 Outer diameter

 Wire diameter

T. Karvinen (



)

Department of Mechanics and Design, Tampere University of Technology,

P.O. Box 589, 33101 Tampere, Finland

e-mail: timo.karvinen@tut.ﬁ

A.C.J. Luo (ed.), Dynamical Systems: Discontinuity, Stochasticity and Time-Delay,

DOI 10.1007/978-1-4419-5754-2

24,

 Springer Science+Business Media, LLC 2010

285

286 T. Karvinen and E. Keskinen

Fig. 24.1 Typical six-stranded wire-rope with (a) independent wire rope core (IWRC), (b)ﬁbre

core, [1] reprinted with permission from Professional Engineering Publishing



Number of wires

 Number of strands

 Strands lay angle

 Lay type: ordinary lay, Lang’s lay

 Core type

 Diameter of core

Material properties of wire ropes are needed in order to perform the dynamic

analysis accurately. Most papers dealing with the dynamic analyses related to ropes

are not actually covering the ropes but belt–pulley systems. The same analysis can

be extended to wire rope – pulley systems using different material properties. A lot

of emphasis is put on the detailed modeling of the belt–pulley contact in the liter-

ature but we try to ﬁnd ways to simplify a complex system consisting of the rope

system, mechanisms, hydraulics, and control systems to more manageable one often

needed in the dynamics analysis.

24 Dynamics of Wire-Driven Machine Mechanisms: Literature Review 287

24.2 Mechanical Properties of Wire Ropes

The wires or strands can be modeled as thin helical rods using [2] curved rod the-

ory. Global relationships between deformation of the cable and the resultant axial

force and bending/torsional moments are established accordingly [3]. There also

exist semicontinuous models in which each layer of helical wires is replaced with

an equivalent orthotropic medium. Interwire and/or interstrand frictional forces are

considered by using contact mechanics to account for stick and slip friction transi-

tion [7]. The individual layers of wires in an axially preloaded multilayered spiral

strand are treated as a series of partly self-stressed cylindrical orthotropic sheets

whose nonlinear elastic properties are averaged to form an equivalent continuum.

The theory is based on the main assumption that with zero axial load on the strand,

the wires in each layer are just touching each other. Under dynamic or cyclic load-

ing, detailed local models overestimate the cable damping for cables with large radii

of curvature. There are analytical approaches and FEM methods [4,9] developed to

calculate cables’ overall mechanical properties which are: axial, bending, torsional

stiffness, and hysteresis characteristics. Depending on the accuracy of the model,

leading to complex mathematical problem, the solution may be unsuitable for large-

scale engineering applications. The most detailed wire cable models have primarily

been developed for static monotonic loading. The mechanical properties exhibit the

following features:

 Young’s modulus is tension dependent

 Stretch consists of two parts: constructional and elastic stretch

 Lay-angle dependent properties

 Interwire friction factor used in simulations  D 0:12

24.2.1 Young’s Modulus

Important concepts in studying the Young’s Modulus are the no-slip and full-slip

limits. The no-slip Young’s modulus is the upper bound to the effective Young’s

modulus. Small disturbances do not induce interwire slippage over the line-contact

patches between adjacent wires in various layers and the wires stick together behav-

ing as a solid bar.

The full-slip Young’s modulus is the lower bound limit whereby wires in line-

contact throughout the strand undergo gross sliding with the interwire frictional

forces becoming insigniﬁcant compared with the axial force changes within indi-

vidual helical wires. The Young’s modulus depends on the loading; therefore one

should measure it at conditions similar to expected working conditions. Analytical

expressions are found in the literature for the effective Young’s modulus taking into

account the geometry, lay angle, number of strands etc. Even though the expressions

are analytic, the calculation of numerical values is quite involving and it may take

some time to write the equations in the computer. The equations of these models are

not presented in this review, apart from some simple expressions. All the equations

288 T. Karvinen and E. Keskinen

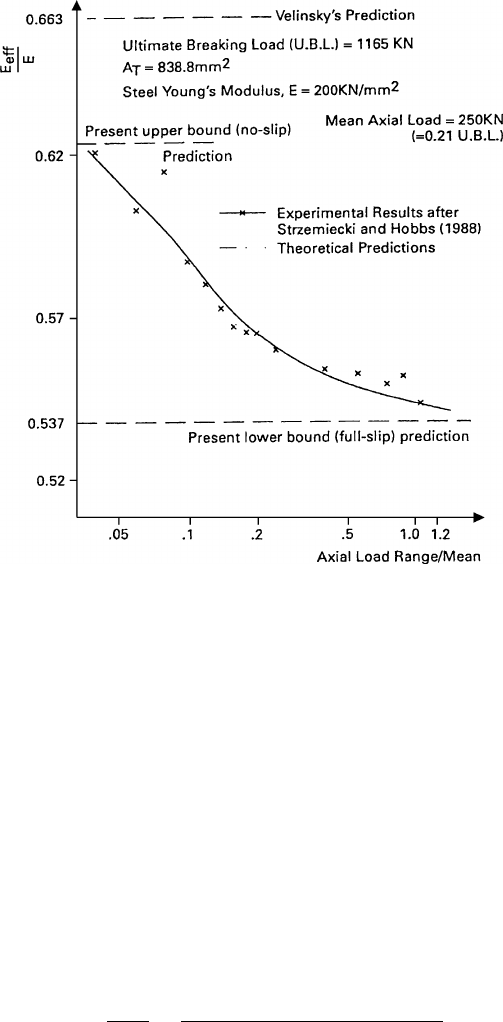
Fig. 24.2 Rope axial stiffness theory vs. experiments, [7] reprinted with permission from ASCE

needed in the calculations can be found in the corresponding papers in the refer-

ence list. There are also models for calculating the stiffness matrix relating the axial

force, moment, and extension and torsion responses [5,6].

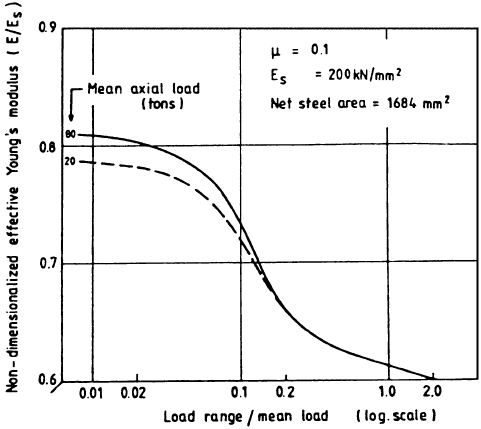
Figure 24.2 illustrates the nondimensional effective Young’s modulus divided by

the steel’s Young’s modulus as a function of the load range obtained both theo-

retically and experimentally. The ﬁgure shows a descending trend for the Young’s

modulus with the increasing load. A similar curve is presented in Fig. 24.3 for other

type of wire rope. Similar curves can be drawn for any wire rope by applying the

calculation procedure and the equations found in, e.g., [7, 8]. Many models found

in the literature are computer based and involve certain iterative procedures. This

potential drawback for practical applications is overcome by some simple methods.

The full-slip values of the Young’s modulus can be calculated from a simple formula

(Hruska’s approach) proposed by [33]

H D

rope

steel

j D1



iD1

cos



cos

j D1



iD1

= cos ˛



cos ˇ

(24.1)

24 Dynamics of Wire-Driven Machine Mechanisms: Literature Review 289

Fig. 24.3 Variation of Young’s modulus as function of loading, [8] reprinted with permission from

Elsevier

in which A

;˛,andˇ are the total cross-sectional area of wires, the lay angle of

wires in a strand, and the lay angle of a strand.

Raoof [1] developed simpliﬁed but still accurate procedures for predicting the

no-slip and full-slip axial stiffnesses of wire ropes, with the proposed formulations

being amenable to simple hand calculations using a pocket calculator. The method

is based on ﬁtting a curve through the data calculated using a more complicated

model. The comparison between Hruska’s and Raoof’s simple models for the full-

slip values is shown in Fig. 24.4.Zhu[9] performed experiments in which the cable

was repeatedly loaded–unloaded, and loaded–unloaded after being bent repeatedly

without tension. It was found out that the elastic modulus changes depending on the

loading: the repeated load applications will increase the elastic modulus of the new

wire cable, and the increased elastic modulus can be lost after bending of the cable

at zero tension.

24.2.2 Damping

Just like in the case of Young’s modulus, analytical models exist for cable damp-

ing [10–12]. The theory for prediction of damping is based on the orthotropic sheet

theory with wire compliances derived from contact stress theories. Later on, [31]

developed simpliﬁed, hand-based procedures for obtaining the maximum values

of axial and/or torsional frictional speciﬁc loss by ﬁtting curves through the data

calculated using a complicated model. A general observation is that the damping

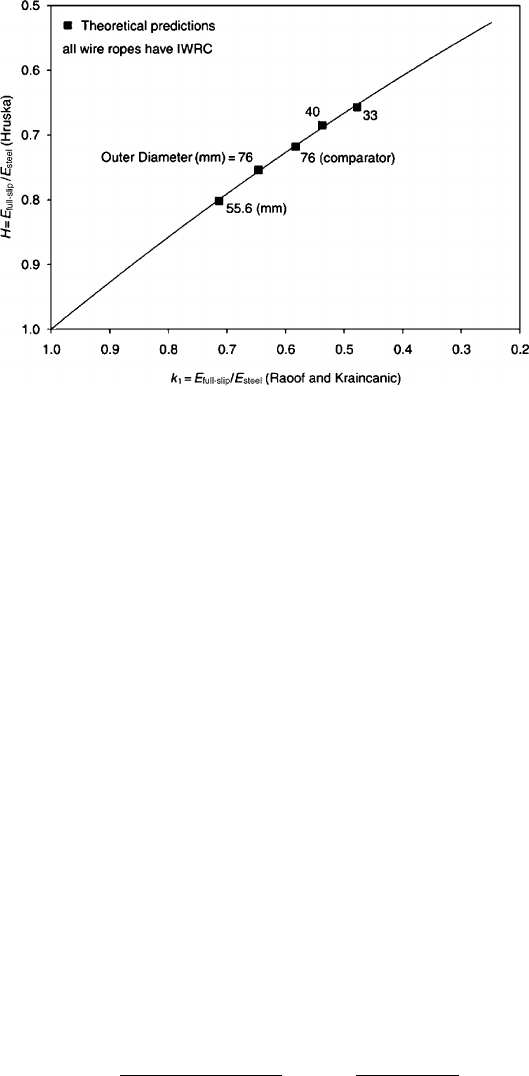
290 T. Karvinen and E. Keskinen

Fig. 24.4 Comparison of different models for calculating Young’s modulus of rope, [1] reprinted

with permission from Professional Engineering Publishing

increases by increasing the number of wires and/or decreasing the helix angle. The

results for damping are presented in a nondimensional form, the x-axis being the

load range divided by the mean load, which should be checked in the paper, and

the y-axis the axial energy loss per cycle divided by the maximum elastic energy,

U=U . This ratio providesthe most direct method of quantifying damping irrespec-

tive of the mechanism involved. For low damping it can be shown that the equivalent

logarithmic decrement is ı

D U=2U . The traditional Coulomb friction model

tends to grossly overestimate cable damping for large radii of curvature in connec-

tion with vortex shedding dynamic instabilities, overhead transmission lines, and

underwater cables where the maximum amplitude of vibration is of the order of one

cable diameter [10]. Figures 24.5 and 24.6 show characteristic damping curves for

strands of different diameters. The curves have a narrow peak at a certain value of

loading indicating maximum damping. There is no easy way to predict at which

value of loading the maximum damping occurs. Damping curves can also be pre-

sented as a function of the Young’s modulus [10].

Figure 24.7 illustrates the damping as a function of radius of curvature. Similar

curves as those found in Fig. 24.7 can be obtained as a function of core-wire radius

ratio, helix angle, and number of wires [12]. It has also been found that the service

time (or number of cycles) increases damping as shown in Fig. 24.8. Besides ana-

lytical models, there exist numerical approaches such as the Rayleigh damping used

for FEM calculations [9])

ŒC D ˛ŒM C ˇŒK; ˛ C !

ˇ D 2

˛ D 2



 !



 !

;ˇD



 !



 !

(24.2)

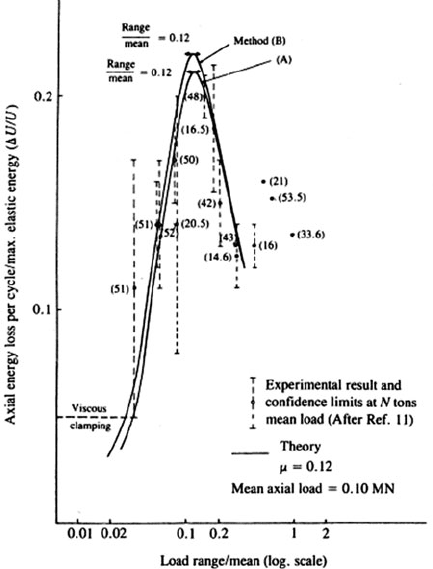
24 Dynamics of Wire-Driven Machine Mechanisms: Literature Review 291

Fig. 24.5 Axial energy dissipation in strands, [11] reprinted with permission from Professional

Engineering Publishing

in which ˛ and ˇ are the damping coefﬁcients multiplying the mass and stiffness

matrices and !

and !

the lower and upper limits of the frequency range of interest.

The Kelvin–Voigt model for damping is employed in simulation of vibrations and

rope stability in one reference [13]. The wear of the rope in bending is discussed,

e.g., in the papers of [14, 15].

24.3 Dynamics Simulation of Wire Rope Systems

There are not many papers in the literature dealing with the system-level analysis of

wire rope systems. Usually the system consists of a belt and two pulleys. Some very

large system level models including the wire rope system, mechanisms, hydraulics,

and control can be found in [16]and[17]. Also if there is a more complicated

mechanism, the system does not fully describe the mechanics and omits, e.g., the

wire stiffness and/or damping.