Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay

Подождите немного. Документ загружается.

312 E. Keskinen et al.

The dynamic behavior of this system has been simulated using the model above

and the results are shown on Figs.25.15–25.17 giving respectively the time variation

of wire tension N , boom contraction force H , boom stress  and tip trajectory

tip

D Œ

tip



in cartesian space.

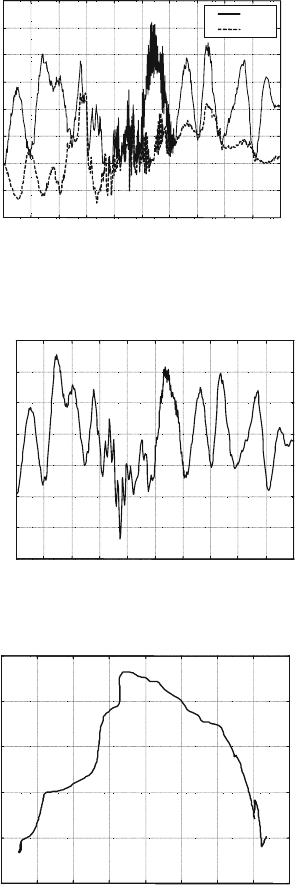
Fig. 25.15 Wire tension N

and actuator force H in boom

shortening cylinder

0 5

t [s]

H [N]

−4000

12000

−4000

12000

N [N]

Fig. 25.16 Bending stress 

variation middle in the ﬁrst

stage of the telescopic link

x 10

t [s]

s [N/m

]

−1

2.5

Fig. 25.17 Trajectory R

tip

the boom tip

3.4 5

4.5

tip

[m]

tip

[m]

25 Dynamics of Wire-Driven Machine Mechanisms 313

Large variation of wire tension is observed on Fig. 25.15 as a result of load

motion and low frequency boom oscillation, which correlates with boom stress on

Fig. 25.16. However, the high frequency generation in the interval between 2 and 3 s.

of boom wire elasticity due to nonlinear friction effect during boom retraction is

almost totally ﬁltered and is only signiﬁcant above threshold stress value. The wan-

dering behavior of tip trajectory on Fig. 25.17 is due to the absence of control and

provides an element on its need. It should be noted that from these plots important

design properties can be directly ﬁxed concerning system and actuator parameters.

25.5.2 Chain Driven Elevating Boom

The second case under study is a hydraulic telescopic boom system consisting of

two links, the ﬁrst one being a chain-driven expandable boom with a rotary joint at

origin to change the latitude angle. The second link is ﬁxed by a rotary joint to ﬁrst

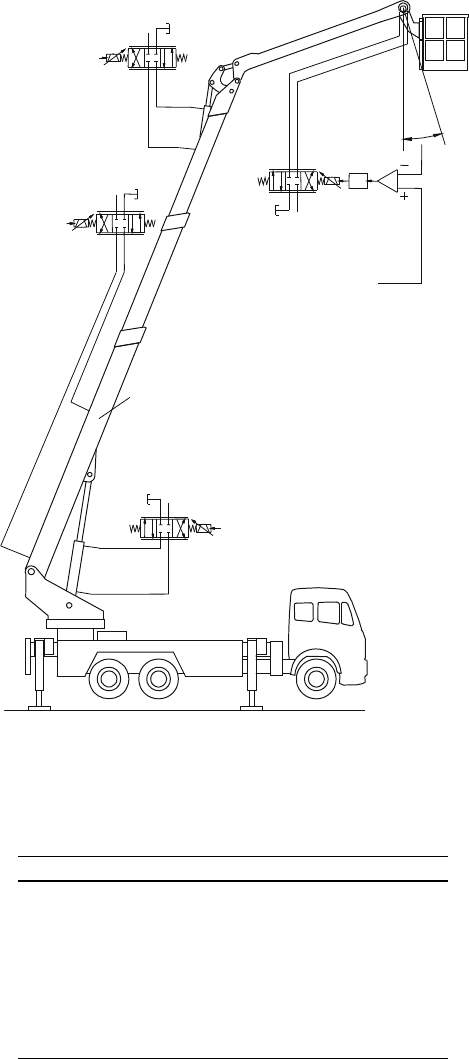
one, and is carrying at its tip an orientable platform, see Figs. 25.1band25.18.

The problem here is to keep the orientation of the platform during operation cycle

of 20 s by applying into platform actuator a PI control subject to orientation error

with the vertical. A similar control has been earlier applied to drive line guiding

in an Excavator-based sheet-piling system [7]. The system model has been built up

and tested on the following maneuver consisting of eight ramp inputs governing the

actuators of ﬁrst two joints and the boom extension.

The sequence of eight actions corresponds to three phases for boom exten-

sion, tilting, and latitude decrease actions in Table 25.4. The actuator of last joint

works during the actions as a part of servo loop for controlling platform verti-

cal orientation.

Simulation of the system corresponding to parameter values of a real industrial

device has been performed. Typical results corresponding to time evolution of chain

tension N and cylinder force H are displayed in Fig. 25.19 while tip trajectory

tip

D Œ

tip



in cartesian space is given in Fig. 25.20.

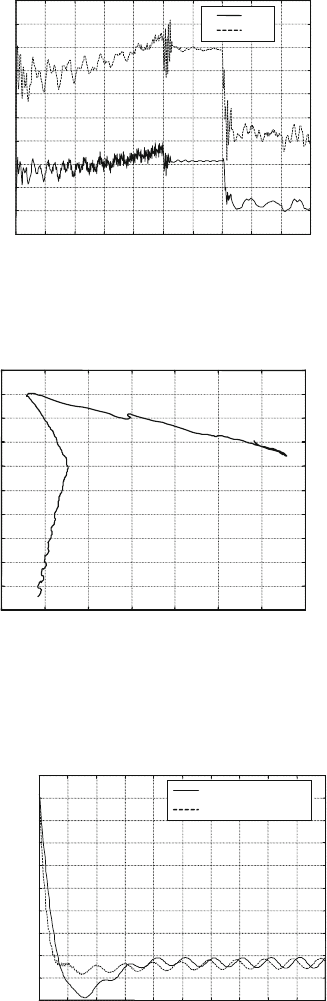
A large variation is observed as in previous case for wire tension. A reason may

be that for the ﬁrst phase between 0 and 10 s, nonlinear friction modes are generated

during boom extension and are transmitted to chain tension through its elasticity.

Mode amplitude is larger than in second phase as they are driven unstable by boom

expansion. This follows from the large and increasing wandering of tip trajectory

on Fig. 25.20 during ﬁrst period with expansion corresponding to the vertical part.

To analyze further the effect of PI-controller, a stationary situation where only

the platform actuator is acting to maintain platform orientation along the vertical has

been considered for two values of the gains. A step drop on time point t D 0 turns

the platform out from the initial vertical orientation to a small negative inclination



D0:015 rad. The step response is given in Fig. 25.21 and will be compared to

the orientation history shown in Fig. 25.22 obtained from the previous maneuver.

Both results show the superposition of two low frequency (f 2) and high fre-

quency (f  20) oscillations coming respectively from boom and from arm natural

314 E. Keskinen et al.

DCV3

DCV2

DCV1

CYL1

CYL2

CYL3

MOT

DCV4

= 0

Fig. 25.18 Chain driven elevating platform

Table 25.4 Sequence of ramp functions in lifting task of the

hydraulic elevating platform

Valve Actuator Switch Ramp Time

DCV1 CYL1 1 C 14:0

DCV2 CYL2 0 N 18:0

DCV3 CYL3 1 C 14:0

DCV4 CYL4 0 N 18:0

DCV5 CYL5 1 N 0:0

DCV6 CYL6 0 N 10:0

DCV7 CYL7 1 C 10:0

DCV8 CYL8 0 N 14:0

25 Dynamics of Wire-Driven Machine Mechanisms 315

Fig. 25.19 Chain tension N

and actuator force H in boom

extension

t [s]

H [N]

5000

N [N]

Fig. 25.20 Trajectory R

tip

of the boom tip

11.5

tip

[m]

tip

[m]

22.5

27.5

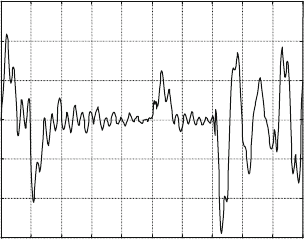
Fig. 25.21 Step responses

of platform orientation ™

at stationary position

= 1, K

= 2

= 2, K

= 1

−3

−18

t [s]

q [rad]

316 E. Keskinen et al.

Fig. 25.22 Platform

orientation ™ during maneuver

020

t [s]

[rad]

−0.03

0.03

vibrations, in the evolution of platform orientation. The behaviors of the two fre-

quencies are different for different values of the gains in the controller. When the

gain for proportional part is small but integral part large, the response is, after slight

overshooting, converging to a constant amplitude oscillation. For larger proportional

gain value but smaller integral gain value, the overshooting peak is eliminated, but

the motion is still converging towards the same vibration.

This oscillation is still not steady-state nor limit-cycle vibration. The reason for

this motion is simply the high ﬂexibility of the long extension boom as compared

with its low internal damping. The time required for this oscillation to die out is

therefore relatively long. PI-controller applied to the platform orientation control

only is not capable to compensate this vibration mode.

This behavior clearly exhibits the limitation of a simple PI-controller to realize

the correct functional transformation required to give the closed loop system asymp-

totically stable behavior, as it will be shown elsewhere.

25.6 Conclusion

The problem of ﬁnding a simple enough PC workable simulation model of

mechanical systems including chains and/or wires in transmission from hydraulic

actuators, and allowing a study of vibration modes, has been addressed to. It was

shown that by homogenization procedure, these continuous parts may in ﬁrst ap-

proximation be represented by their stiffness characterizing their tension during

time evolution. The resulting model description has been studied for two industrial

applications kinematical corresponding to open and closed loop structures. In both

cases, wire or chain tension has been directly obtained with the other variables and

system vibrations can be analyzed. The present simulation model allows to directly

compare the consequences of different choice of nominal parameters onto system

dynamics. The effect of various controllers can as well be discussed. In this sense,

the proposed model is providing an adequate tool for system design.

25 Dynamics of Wire-Driven Machine Mechanisms 317

References

1. Karvinen T, Keskinen E (2009) Dynamics of wire-driven machine mechanisms, Part I – liter-

ature review. Dynamical system with discontinuity, stochasticity and time-delay. (A.C.J. Luo,

ed., Springer), 285–298

2. Keskinen E, Keskiniva E, Riitahuhta A (1995) Utilization of integrated simulation techniques

for rapid prototyping of mechatronic machines. Invited Lecture Proceedings ICRAM’95, vol I.

p 111

3. Keskinen E, Montonen J, Launis S, Cotsaftis M (1999) Simulation of wire and chain mecha-

nisms in hydraulic driven booms. In: IASTED international conference on applied modelling

and simulation, Cairns, QLD, September 1–3 1999

4. Keskinen E, Montonen E, Launis S, Cotsaftis M (1999) Cartesian trajectory control of hydraulic

elevating platforms. In: IASTED International conference on robotics and applications, Santa

Barbara, CA, 28–30 October 1999

5. Keskinen EK, Iltanen M, Salonen T, Launis S, Cotsaftis M, Pispala J (2000) Man-in-the-loop

training simulator for hydraulic elevating platforms. In: Proceedings of 17th IAARC/IFAC/IEEE

international symposium on automation and robotics in construction, Taipei, Taiwan, 18–20

September 2000

6. Keskinen EK, Iltanen M, Salonen T, Launis S, Cotsaftis M, Pispala J (2001) Dynamics of train-

ing simulator for mobile elevating platforms. In: Arai E, Arai T, Takano M (eds) Human friendly

mechatronics. Elsevier Science B.V., Amsterdam

7. Keskinen E, Launis S, Cotsaftis M, Raunisto Y (2001) Performance analysis of drive line steer-

ing methods in excavator-mounted sheet-piling systems. Comput Aided Civil Infrastruc Eng

16(4):229–238

Chapter 26

On Analytical Methods for Vibrations of Soils

and Foundations

H.R. Hamidzadeh

Abstract Research on dynamics of soils and foundations has yielded several

fundamental methods for formulation of interaction problems. This paper is in-

tended to survey the development of the current state-of-practice for design and

analysis of dynamically loaded foundations. Extensive studies in this ﬁeld utilize

various linear mathematical models for interaction between foundations and differ-

ent soil media. The effective analytical, numerical, and experimental techniques and

their methodologies, which are well established for treating problems in dynamic

soil-foundation interaction are outlined. Described techniques are categorized based

upon formulation procedures and their applications. Some areas are indicated where

further research is needed.

26.1 Introduction

The possible occurrence of extreme dynamic excitation, either natural or manmade,

has a major inﬂuence on the design of buildings and machine foundations. A pri-

mary concern in designing foundations is the knowledge of how they are expected to

respond when subjected to dynamic loadings. The validity of the mathematical anal-

ysis depends entirely on how well the mathematical model simulates the behavior of

the real foundation. Over the past decades, our ability to analyze mathematical mod-

els for dynamics of foundations has been improved by the use of different analytical

and numerical techniques. In most of these analyses, it is common to assume that the

footing is rigid and the medium is a homogeneous elastic half-space. Extensive ef-

forts have been conﬁned in the development of procedures and computer simulations

to tackle some practical problems that arise in this ﬁeld, while other important prob-

lems have been neglected. It should be noted that interaction between foundations

H.R. Hamidzadeh (



)

Department of Mechanical and Manufacturing Engineering, Tennessee State University,

Nashville, TN, USA

e-mail: HHamidzadeh@tnsate.edu

A.C.J. Luo (ed.), Dynamical Systems: Discontinuity, Stochasticity and Time-Delay,

DOI 10.1007/978-1-4419-5754-2

26,

 Springer Science+Business Media, LLC 2010

319

320 H.R. Hamidzadeh

for noncircular footings was not treated in a satisfactory manner and signiﬁcant

deﬁciencies remain in most of the previous analyses.

This paper will discuss some of the issues of dynamics of soils and foundations

from a practical point of view. Since this topic is quite broad, a brief description

of methodology will be outlined, while details will be given for a few procedures

that have proven to be effective and accurate. One of the main objectives of this

review paper is to survey different available techniques for solving the dynamic re-

sponse of foundations when subjected to harmonic loadings. Special attention is

directed to the dynamic response of the surface of the medium due to concentrated

dynamic loads, response of foundations, coupled vibrations of foundations, interac-

tion between two foundations, experimental aspects of soils and foundations, and

laboratory simulations.

26.2 Surface Response Due to Concentrated Forces

In the ﬁeld of propagation of disturbances on the surface of an elastic half-space,

the ﬁrst mathematical attempt was made by Lamb [1]. He gave integral representa-

tions for the vertical and radial displacements of the surface of an elastic half-space

due to a concentrated vertical harmonic force. Evaluation of these integrals involves

considerable mathematical difﬁculties, due to the evaluation of a Cauchy principal

integral and certain inﬁnite integrals with oscillatory integrands. Nakano [2] consid-

ered the same problem for a normal and tangential force distribution on the surface.

Barkan [3] presented a series solution for the evaluation of integrals for the ver-

tical displacement caused by a vertical force on the surface, which was given by

Shekhter [4]. Pekeris [5, 6] gave a greatly improved solution to this problem when

the surface motion is produced by a vertical point load varying with time, like the

Heaviside function. Elorduy et al. [7] developed a solution by applying Duhamel’s

integral to obtain the harmonic response of the surface of an elastic half-space due

to a vertical harmonic point force. Heller and Weiss [8] studied the far ﬁeld ground

motion due to an energy source on the surface of the ground.

Among the investigators who considered the three-dimensional problem for a

tangential point force, Chao [9] presented an integral solution to this problem for an

applied force varying with time like the Heaviside unit function. Papadopulus [10]

and Aggarwal and Ablow [11] have presented solutions, in integral expressions, to a

class of three-dimensional pulse propagation in an elastic half-space. Johnson [12]

used Green’s functions for solving Lamb’s problem, and Apsel [13]employed

Green’s functions to formulate the procedure for layered media. Kausel [14]re-

ported an explicit solution for dynamic response of layered media. Davies and

Banerjee [15] used Green’s functions to determine responses of the medium due

to forces that were harmonic in time with a constant amplitudes. The solution was

derived from the general analysis for impulsive sources. Kobayashi and Nishimura

[16] utilized the Fourier transform to develop a solution for this problem, and

expressed the results in terms of the full-space Green’s functions, which include

26 On Analytical Methods for Vibrations of Soils and Foundations 321

inﬁnite integrals of exponential and Bessel’s function products. Banerjee and

Mamoon [17] provided a solution for a periodic point force in the interior of a

three-dimensional, isotropic elastic half-space by employing the methods of synthe-

sis and superposition. The solution was obtained in the Laplace transform as well

as the frequency domain.

Hamidzadeh [18] presented mathematical procedures for determination of the

dynamic response of surface of an elastic half-space subjected to harmonic load-

ings and provided numerical results for displacement of any point on the surface

in terms of properties of the medium and of the exciting force. The solution was

analytically formulated by employing double Fourier transforms and was presented

by integral expressions. Hamidzadeh [19] and Hamidzadeh and Chandler [20]pro-

vided dimensionless response for an elastic half-space and compared their results

with other available approximate results.

Considering a semi-inﬁnite elastic solid subjected to a vertical concentrated har-

monic force as illustrated in Fig. 26.1, the radial and vertical displacements on the

surface of the medium due to applied load can be expressed as:

u.r/ D

C iu

/ e

i!t

(26.1)

v.r/ D

C iv

/ e

i!t

(26.2)

where a

D r! =G is frequency factor, F

and ! are amplitude and angular

frequency of the applied force, respectively. G and  are shear modulus and density

of the medium, respectively. u and v are radial and vertical displacement at any point

on the surface. u

C iu is a complex non-dimensional radial displacement function.

C iv

is a complex non-dimensional vertical displacement function.

Figure26.2 presents numerical results computed for the displacements on the

surface of semi-inﬁnite elastic medium. The displacements of a point on the surface

Semi-infinite

Solid

iΤt

Fig. 26.1 Surface of a semi-inﬁnite elastic solid subjected to a vertical concentrated harmonic

force

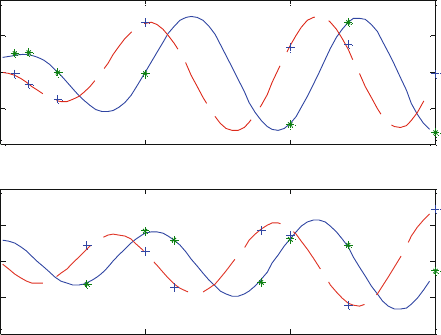
322 H.R. Hamidzadeh

0 5 10 15

−0.2

−0.1

0.1

0.2

−u1,u2

−u1

0 5 10 15

−0.4

−0.2

0.2

0.4

−v1,v2

Frequency Factor - a0

−v1

Fig. 26.2 Complex non-dimensional radial and vertical functions vs. frequency factor a

(Hamidzadeh’s – lines; and Rucker’s – symbols)

of the medium depend largely upon in-phase and quadrature components of the

non-dimensionalized complex displacement functions. These components are func-

tions of frequency factory. The range of frequency factor covered is more than

sufﬁcient for practical purposes of considering near-ﬁeld displacements. Far-ﬁeld

displacements can be determined using Lamb’s equations. The values of u

, u

, v

and v

are for Poisson’s ratio of 0.25.

26.3 Dynamic Response of Foundations

Advances in the development of solutions for soil-foundation interaction problems

are categorized in the following sections based on the formulation procedures.

26.3.1 Assumed Contact Stress Distributions

The ﬁrst attempt to solve the vertical vibration of a massive circular base on the

surface of an elastic medium was made by Reissner [21]. He adopted Lamb’s [1]

approach and developed a solution by assuming a uniform stress distribution on the

surface of the medium. He established an estimated solution for determining the

vertical steady state response of circular footings. He also calculated the displace-

ment of the center of the base and introduced the amplitude of vibration in terms of