Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay

Подождите немного. Документ загружается.

26 On Analytical Methods for Vibrations of Soils and Foundations 323

non-dimensional parameters. It has been proven that his results overestimated the

amplitude due to his consideration of the displacement at the center of the base.

Reissner and Sagoci [22] presented a static solution for the torsional oscillation of a

disc on the medium. Miller and Pursey [23,24] considered the vertical response of

a circular base due to a force uniformly distributed on the contact surface. Quinlan

[25] and Sung [26] independently extended Riessner’s [21] approach to solve the

problem of vertical vibration of circular and inﬁnitely long rectangular footings.

In their analyses, they considered three different harmonic stress distributions: uni-

form, parabolic, and stress produced by a rigid base under static conditions. They

showed that the vibration characteristics of semi-inﬁnite media effectively vary with

the type of stress distributions and elastic properties of the medium.

Arnold et al. [27] considered four vibrational modes (vertical, horizontal, tor-

sional, and rocking) for a circular base on the surface of elastic media. By assuming

harmonic static stress distributions for all modes, they evaluated the dynamic

responses using an averaging technique. They also veriﬁed this work with experi-

mental results using a ﬁnite model for the inﬁnite medium. Bycroft [28] followed the

same approach for four modes of vibration by determining complex functions to rep-

resent the in-phase and out-of-phase components of displacement of a rigid massless

circular plate. Bycroft [29] later carried out some tests to verify his previous theo-

retical work. Thomson and Kobori [30] and Kobori et al. [31–35] considered the

dynamic response of a rectangular base. They provided computational results for

components of the complex displacement functions by assuming a uniform stress

distribution on the contact area of the base and medium. Their analysis was for an

elastic half-space, viscoelastic half-space, and layered viscoelastic media.

26.3.2 Mixed Boundary Value Problems

Harding and Sneddon [36] and Sneddon [37] gave a static solution for a rigid circu-

lar punch pressed into an elastic half-space. By the use of the Hankel transform, the

appropriate mixed boundary value problem was reduced to a pair of dual integral

equations representing the stress distribution and uniform displacement under the

rigid punch.

Several investigations have been conducted to extend the static solution to the

corresponding dynamic problems. Awojobi and Grootenhuis [38] and Awojobi

[39–42] used the Hankel transform to present the complete dynamic problem by

dual integral equations. They gave an analytical solution for the vertical and tor-

sional oscillations of a circular body and the vertical and rocking modes of an

inﬁnitely long strip foundation. The evaluation of stress distributions and uniform

displacements was based on the extension of the Titchmarsh’s [43] dual integral

equation and a method of successive approximations. Robertson [44, 45] followed

the same procedure and reduced the dual integral equations into Fredholm integral

equations and gave series solutions to these equations for the vertical and torsional

response of a rigid circular disc. Gladwell [46–48] developed a solution for the

324 H.R. Hamidzadeh

mixed boundary value problems for circular bases resting on an elastic half-space

or elastic strata. He solved the integral equations and presented the displacements

of four different modes of vibration in series forms. Karasudhi et al. [49] treated

the vertical, horizontal, and rocking oscillations of a rigid strip footing, on an elas-

tic half-space, by reducing the dual integral equations into the Fredholm integral

equations. Housner and Castellani [50] conducted an analytical solution based on

the work done by the total dynamic force and determined the weighted average ver-

tical displacement for a cylindrical body. To determine the free ﬁeld displacements

of an elastic medium, for four different modes of vibration, for a cylindrical body,

Richardson [51] followed Bycroft’s [28] method and provided a solution to this

problem. Luco and Westmann [52] solved the mixed boundary value problems for

four modes of vibration by considering a massless circular base. Their procedure

reduced the resulting dual integral equations to the Fredholm integral equations.

They calculated the complex displacement functions for a wide range of frequency

factors. In a separate publication [53], they followed the same procedure for the

determination of the response of a rigid strip footing for the three modes of ver-

tical, horizontal, and rocking vibration. The vibration of a circular base was also

treated by Veletsos and Wei [54] for horizontal and rocking vibrations. Bycroft [55]

extended his earlier work to present approximate results for the complex displace-

ment functions at higher frequency factors. Veletsos and Verbic [56] introduced the

vibration of a viscoelastic foundation. Clemmet [57] included hysteretic damping

in the Richardson [51] solution. Luco [58] provided a solution for a rigid circular

foundation on a viscoelastic half-space medium.

These investigations were based on circular or inﬁnitely long strip foundations.

Few investigators have paid attention to the dynamic responses of a rectangular

foundation, due to the difﬁculty of the asymmetric problem. Elorduy et at. [7]in-

troduced a numerical technique based on the uniform displacements for a number

of points on the contact surface of the rectangular footings. In their analysis, they

employed an approximate solution for the surface motion of a medium due to a ver-

tical point force. They gave complex displacement functions for vertical and rocking

modes with different ratios of length to width of rectangular footings. By extending

the Bycroft [29] idea of an equivalent circular base for a rectangular foundation,

Tabiowo [59] and Awojobi and Tabiowo [60] gave a solution to this problem. They

also introduced another solution by superimposing the solution of two orthogonal

inﬁnitely long strips and gave the displacement at the intersection of these strips

for different frequencies. Wong and Luco [61,62] solved this problem for the three

modes of vertical, horizontal, and rocking vibrations. They used the approach re-

ported by Kobori et al. [31] to provide an approximate solution to a footing, which

was divided into a number of square subregions. They assumed that the stress dis-

tribution for each subregion is uniform with unknown magnitude, while all the

subregions experienced uniform displacements. Their solution considered the cou-

pling effect for viscoelastic medium, and the complex stiffness coefﬁcients were

tabulated [62] for different loss factors.

Hamidzadeh [18] and Hamidzadeh and Grootenhuis [63] presented an improved

version of Elorduy’s method to obtain the dynamic responses for three modes of ver-

tical, horizontal, and rocking vibration for rectangular foundations. In their analysis,

26 On Analytical Methods for Vibrations of Soils and Foundations 325

a uniform displacement for each node of rectangular subregions were assumed.

They utilized the impedance matching technique to formulate the dimensionless

response for foundations.

As reported by Hamidzadeh and Grootenhuis [63], vertical, horizontal, and rock-

ing displacements of a rigid massless base resting on an elastic half-space can be

expressed conveniently in terms of two non-dimensional displacement functions,

one in-phase with the motion (F

) and the other in quadrature (F

) such that: for

vertical displacements one may write:

C F

/ (26.3)

for horizontal displacement it yields

C iF

/ (26.4)

and ﬁnally for rocking motion it results



C iF

/: (26.5)

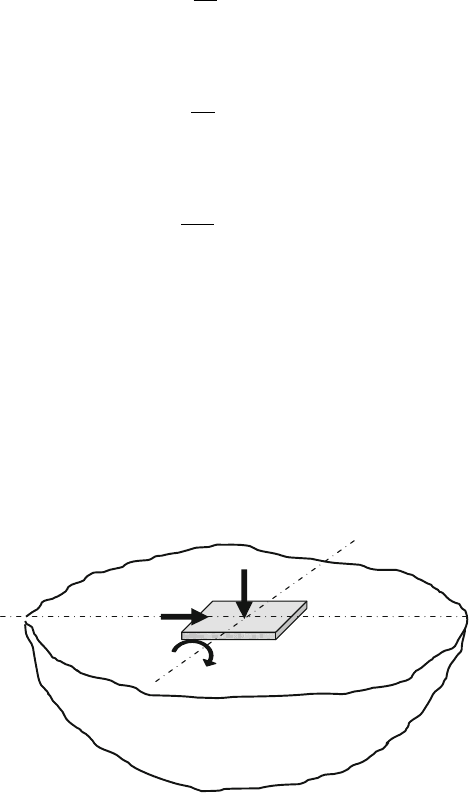
As shown in Fig. 26.3. F , P ,andM are the applied harmonic vertical force, hori-

zontal force, and the moment. G is the shear modulus of the medium, and c is the

half width of the square base. The numerical values of the displacement functions

and F

, for the different uncoupled motions with subscripts V for vertical, H for

horizontal, and R for rocking, have been computed for a square base. The abscissa

is the frequency factor

a D !c=c

(26.6)

where ! is the excitation frequency in rad/s, d is half the width of one side and

is the velocity of shear waves in the medium. The displacement functions have

Fig. 26.3 A rectangular rigid foundation on the surface of an elastic half-space subjected to

harmonic vertical, horizontal, and rocking excitation forces and moment

326 H.R. Hamidzadeh

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6

0.1

0.2

−V1,V2

Vertical

−V1

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6

0.1

0.2

−H1,H2

Horizontal

−H1

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6

0.1

0.2

−R1,R2

Frequency Factor - a

Rocking

−R1

Fig. 26.4 Variation of non-dimensional displacements functions vs. frequency factor a for vertical,

horizontal, and rocking motions

been calculated for a frequency factor up to 1.6 where necessary for the subsequent

computation of the resonant response of a foundation block.

The results presented in Fig. 26.4 are for a Poisson’s ratio of 0.25, which is a

reasonable value to take for certain types of soil. Similar sets of curves have been

computed for values of Poisson’s ratio of 0, 0.31, and 0.5 (given in [18]).

The in-phase function, F

, gives a measure of the stiffness of the elastic half-

space whereas the quadrature function, F

, is dependent upon the amount of energy

radiated into the half-space. The amplitude response at resonance of a massive foun-

dation block, is therefore controlled solely by the quadrature function. To evaluate

the dynamic response of a foundation block the displacement functions and the

impedance matching technique will be used. The assembled systems of a mass, m,

or of an inertia, I , and a half-space for the three motions can be split into compo-

nents of mass or inertia and medium. The axis of rocking has been taken through the

centre point, O, in the base of the block. The impedance of the rigid body is deﬁned

as the ratio of the applied force divided by the resultant velocity. Since the applied

force and moment are harmonic, the displacements given by (26.5) can be trans-

formed into velocities. By adding the component impedances, the non-dimensional

amplitude of vibration for each mode can be expressed as:

Vertical

jGc

C F

.1 C a

C .a

1=2

(26.7)

Horizontal

jGc

C F

.1 C a

C .a

1=2

(26.8)

26 On Analytical Methods for Vibrations of Soils and Foundations 327

Rocking

j

jGc

C F

.1 C a

C .a

1=2

; (26.9)

where a is the frequency factor, b and b

are the mass and inertia ratios deﬁned as:

b D

c

(26.10)

c

(26.11)

and  is the density of the medium.

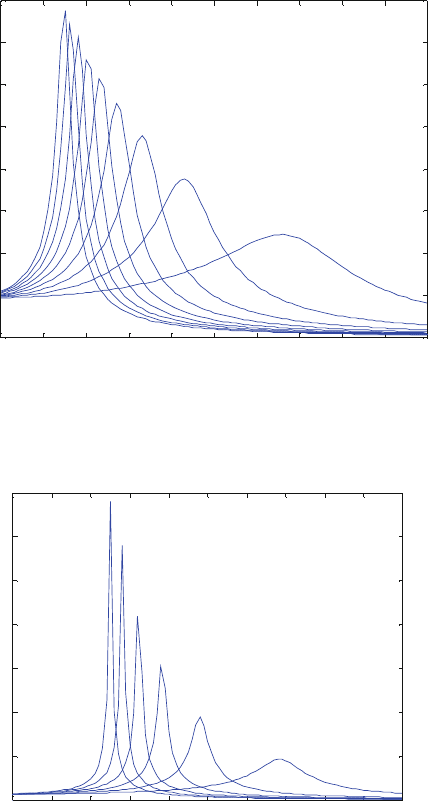
The amplitude factors have been plotted in Figs. 26.5–26.7 as a function of the

frequency factor a for constant square base for a Poisson’s ration of 0.25. It can be

seen from these frequency response curves that the lower the mass or inertia ratio

the lower the maximum value of the amplitude factor and the higher the value of the

frequency factor at which this maximum occurs.

It may seem rather surprising at ﬁrst that a foundation block with a high mass

or inertia ratio will respond more vigorously at resonance than another block with

lower values for the same ratio, when each is exposed to the same disturbing forces

or moments. The energy radiated into the inﬁnite half-space will be less in propor-

tion to the kinetic energy of the vibrating system for the higher values of the mass or

inertia ratio than for the lower values, and hence there will be less effective damping

at resonance. For very low values of the mass ratio for vertical and for horizontal

forcing, all the energy is radiated into the half-space and there is then no resonant

response.

0 0.2 0.4 0.6 0.8 1 1.2 1.4

0.1

0.2

0.3

0.4

0.5

Non-dimensionalized amplitude - V

Non-dimensionalized frequency - a

b=10

Poisson ratio = 0.25

Fig. 26.5 Non-dimensional amplitude vs. frequency at different mass ratios for vertical harmonic

vibration

328 H.R. Hamidzadeh

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1

0.2

0.4

0.6

0.8

1.2

1.4

1.6

Non-dimensionalized amplitude - U

Non-dimensionalized frequency - a

b=10

Poisson ratio = 0.25

Fig. 26.6 Non-dimensional amplitude vs. frequency at different mass ratios for horizontal

harmonic vibration

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1

Non-dimensionalized rocking amplitude

Non-dimensionalized frequency - a

b=10

Poisson ratio = 0.25

Fig. 26.7 Non-dimensional amplitude vs. frequency at different Inertia ratios for rocking

harmonic vibration

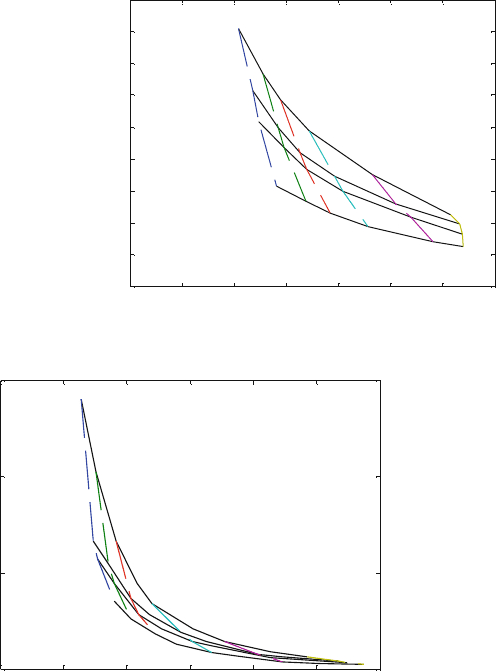
Another important parameter that has a signiﬁcant effect on the dynamic re-

sponse is the Poisson’s ratio. Previous numerical results [1, 12]haveshownthat

the resonant amplitude factor will decrease when the Poisson’s ratio of the medium

is increased. The effects of mass ratio and of Poisson’s ratio on the frequency

factor at resonance and the amplitude factor for the three modes are shown in

26 On Analytical Methods for Vibrations of Soils and Foundations 329

Fig. 26.8 Non-dimensional

amplitude vs.

non-dimensional resonant

frequency for different mass

and Poisson ratios for vertical

harmonic vibration

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

b=120

ν = 0.0

0.25

0.31

0.5

Resonant Frequency Factor

Resonant Amplitude Factor

0 0.2 0.4 0.6 0.8 1 1.2

Resonant Frequency Factor

Resonant Amplitude Factor

b=80

ν = 0.0

0.25

0.31

0.5

Fig. 26.9 Non-dimensional amplitude vs. non-dimensional resonant frequency for different mass

and Poisson ratios for horizontal harmonic vibration

Figs. 26.8–26.10. These results play an important part in the design of a foundation

block. The variation of the resonant frequency factor and the amplitude factor can be

explained physically by the change in stiffness, which accompanies a variation in

Poisson’s ratio.

An approximate method for computation of compliance functions of rigid plates

resting on an elastic or viscoelastic half-space excited in all directions was re-

ported by Rucker [64]. The proposed method provides compliances for vertical,

horizontal, rocking, and torsional motion for rectangular foundations. Another ap-

proximate solutions for harmonic response of an arbitrary shape foundation on an

elastic half-space was reported by Chow [65]. In his analysis, the contact area was

discretized into square subregions, and the inﬂuence of the square subregion was

330 H.R. Hamidzadeh

0 0.2 0.4 0.6 0.8 1 1.2

0.2

0.4

0.6

0.8

1.2

1.4

1.6

Resonant Frequency Factor

Resonant Amplitude Factor

b′ = 60

ν = 0.0

0.25

0.31

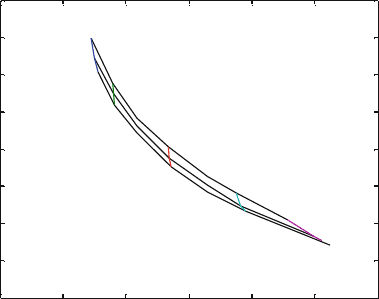
Fig. 26.10 Non-dimensional amplitude vs. non-dimensional resonant frequency for different

inertia and Poisson ratios for rocking harmonic vibration

approximated by that of an equivalent circular base. He then compared his results

with those of Wong and Luco [62] and Hamidzadeh and Grootenhuis [63]. The dy-

namic stiffness of a rigid rectangular foundation on the half-space was considered by

Triantafyllidis [66] who provided solutions for the mixed-boundary value problem.

The problem was formulated in terms of coupled Fredholm integral equations of

the ﬁrst kind. The displacement boundary value conditions were satisﬁed using the

Bubnov–Galerkin method. The solution yielded the inﬂuence functions and the stiff-

ness functions characterizing the dynamic interaction between the foundation and

half-space. The presented analytical method considered the coupling between nor-

mal and shear stress distributions acting on the contact area between the footing and

the half-space.

26.3.3 Lumped Parameter Models

Based on the theoretical work for the response of a rigid massless circular plate,

Hsieh [67] was able to present equivalent mass-spring-dashpot models for all

four modes of vibration. The calculated dynamic parameters for each mode were

frequency dependent. Following the Hsieh’s approach, Lysmer [68] provided fre-

quency independent values for equivalent spring and damping constants. The idea

of developing an equivalent mass-spring-dashpot model for a rigid mass on the sur-

face of a half-space has attracted many investigators such as Lysmer and Richart

[69], Weissmann [70], Whitman and Richart [71], Hall [72], Veletsos and Wei [54],

Roesset et al. [73], Oner and Janbu [74], Hall et al. [75], and Veletsos [76]. Approx-

imate expressions for the dynamic stiffness coefﬁcients in the frequency domain are

26 On Analytical Methods for Vibrations of Soils and Foundations 331

well established, and are summarized in a text by Wolf [77]. Lumped parameter

models to represent the soil-structure interaction for embedded foundations were

developed by Wolf [78]. Dobry and Gazetas [79, 80] presented a method to deter-

mine the effective dynamic stiffness and damping coefﬁcient of a rigid footing by

considering variations of foundation shape, soil type, and length ratio of the base.

The analytical methods employed were those of Wong and Luco [60], and they veri-

ﬁed some of their computations by several in-situ experiments. A different approach

based on the subgrade reaction method is also reported by many investigators such

as Terzaghi [81, 82], Barkan [3], and Girard [83].

26.3.4 Computational Methods

The Finite Element Method (FEM) has been applied to discretize foundations, the

most crucial problem for discretization of foundations by FEM is transmitting waves

through artiﬁcial ﬁnite boundaries. This is considered to be a drawback, which is

due to the difﬁculty encountered in proper modeling of an unbounded soil medium

and satisfying the wave radiation condition. The problem of a rigid circular base

on an elastic half-space has been considered numerically by many investigators such

as Duns and Butterﬁeld [84], Lysmer and Kuhlemeyer [85], and Seed et al. [86].

However, these solutions have not been generalized to cover all modes of vibration

due to numerical limitations. Day and Frazier [87] suggested the use of artiﬁcial

boundaries far away from the region of interest to avoid the undesirable wave re-

ﬂections. Bettess and Zienkiewicz [88] recommended the use of inﬁnite elements

and Roesset and Ettouney [89], and Kausel and Tassoulas [90] proposed transmit-

ting or non-reﬂecting boundaries to circumvent the problem. Chuhan and Chongbin

[91] presented an approximate solution for a viscoelastic medium and strip foun-

dation by considering two-dimensional wave equations in conjunction with the use

of Galerkin weighted residual approximations. A frequency-dependent compatible

inﬁnite element was presented, then by coupling the inﬁnite elements with ordinary

ﬁnite elements the system was used to simulate the propagation of waves.

The boundary element method (BEM) has been used as an effective numerical

technique for solving elastodynamic problems. In this method, boundary integral

representation provides an exact formulation, and the only approximations are those

due to the numerical implementation of the integral equations. The technique is

suitable for inﬁnite and semi-inﬁnite domain due to employment of Green’s func-

tions, which satisfy the radiation condition at far-ﬁeld. The ﬁrst application of

this technique on soil-structure interaction was performed by Dominguez [92],

and Dominguez and Roesset [93] in frequency domain. Karabalis and Beskos [94]

determined the frequency and time domain solutions for dynamic stiffness of a rect-

angular foundation resting on an elastic half-space medium. Spyrakos and Beskos

[95, 96] used the time domain boundary element method to consider dynamic re-

sponse of two-dimensional rigid and ﬂexible foundations.

332 H.R. Hamidzadeh

Numerical solutions for a layered medium are reported by Luco and Apsel

[97] and Chapel and Tsakalidis [98]. In these solutions, formulation for Green’s

functions were made using the Hankel transform for each layer. Kausel [14]

presented an explicit closed-form solution for the Green’s functions corresponding

to dynamic loads acting on layered strata. These functions embody all the essential

mechanical properties of the medium. The solution is based on a discretization

of the medium in the direction of layering, which results in a formula yielding

algebraic expressions for the displacement of all layers. Determination of response

for a layered medium to dynamic loads, prescribed at some location in the soil, can

be achieved by using the stiffness matrix method presented by Kausel and Roesset

[99]. In their solution the external loads, applied at the layer interfaces, are related to

the displacements at these locations through stiffness matrices, which are functions

of both frequency and wave number. The proposed method can treat simultaneous

solutions for multiple loadings. Israil and Ahmad [100] investigated the dynamic

response of rigid strip foundations on different media of a viscoelastic half-space,

viscoelastic strata on a half-space, and viscoelastic strata on a rigid bed. An ad-

vanced boundary element algorithm was developed by incorporating isoparametric

quadratic elements. The effect of Poisson’s ratio and material damping, layer depth,

embedment, and type of contact at the foundation-medium interface was studied.

26.4 Coupled Vibrations of Foundations

In the analyses for the pure rocking or the horizontal mode, it is usual to assume that

the medium is rigidly stiff for either shear or compression deformations. However, it

is known from characteristics of the soil that it can resist elastically for both applied

compression and shear. Therefore, the problem of horizontal or rocking motion for a

massive footing on the surface of elastic half-space media should be considered as a

coupled motion. Wong and Luco [61,62], Rucker [64], and Triantafyllidis [66]have

presented solutions for coupled vibrations of rectangular foundations on an elastic

and viscoelastic half-space.

Another approximate solution is based on simultaneous horizontal and rocking

motions. Hall [72] is among the early investigators who used the solution for pure

sliding and rocking of circular bases. He followed the Hsieh [67] approach in de-

riving the equations for simultaneous motion and presented numerical results for

certain cases. Richart and Whitman [101] compared the experimental results ob-

tained by Fry [102] with a similar prediction that Hall introduced for a circular base.

They found that their comparisons were satisfactory. Karasudhi et al. [49]andLuco

and Westmann [53] provided an approximate solution to the problem of the coupled

motion of an inﬁnitely long rigid strip. Veletsos and Wei [54] introduced an approx-

imate solution to evaluate the stiffness and damping coefﬁcients for a massless rigid

circular footing. They also compared these coefﬁcients with their corresponding

value for simultaneous motion. Ratay [103] considered simultaneous motions when

the circular base is excited by a harmonic horizontal force. He studied the variation

of the frequency response curve due to variation of involved parameters. Beredugo