Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay

Подождите немного. Документ загружается.

27 Inversely Found Elastic and Dimensional Properties 353

Table 27.2 Comparing conventionally measured values with those recovered ultrasonically

Property Conventional approach Ultrasonic approach

Young’s modulus, E (GPa) 202 ˙6 200 ˙10

Lam´e constant [Shear modulus],  [G](GPa) 79 ˙282˙3

Lam´e constant,  (GPa) 99 ˙54 68 ˙8

Ratio of Lam´e constants, .=/ 1:3 ˙ 0:7 0:84 ˙ 0:06

Poisson’s ratio, 0:28˙0:07 0:228 ˙0:009

Outer diameter, D

(mm) 88:80 ˙ 0:09 –

Thickness, H (mm) 5:6 ˙0:1 5:59 ˙ 0:01

Mean radius, R (mm) 41:6 ˙0:1 41:60 ˙0:05

Thickness to mean radius ratio, .H=R/ 0:134˙0:003 0:1343 ˙ 0:0004

Mass density,  (kg=m

) 7;700 ˙ 200 –

27.6.2 Experimental Corroboration

An actual 80 mm DN, Schedule 40, seamless, carbon steel pipe was examined ex-

perimentally next. The radial displacement was measured on the pipe’s outer surface

at   0 and z



D z=H  5. The time history is presented in Fig. 4a, while the

corresponding DFT and temporal curve ﬁt are given in Figs. 4c and 4b, respec-

tively, of [19]. The inversion procedure and uncertainty estimation were applied to

the cut-off frequencies obtained from the temporal curve ﬁt. Results from the ultra-

sonic measurements are summarized in Table 27.2.

An 18 cm or so length was cut from one end of the pipe. Plates and grips

were welded onto this short sample after which the sample was heat treated to re-

lieve residual stresses. Two nominally identical, three-element strain gauge rosettes

were bonded to the specimen. Then the instrumented sample was mounted in a stan-

dard pseudo-static test frame and loaded in either tension-compression or torsion.

The tension-compression results were used to estimate Young’s modulus, E;thetor-

sional test gave the shear modulus, G. These values are also reported in Table 27.2,

along with the independently determined mass density, outer diameter, and wall

thickness. It can be seen that E, G, and dimensional information found from the

ultrasonic measurements correlate very well with those obtained pseudo-statically.

However, the conventional, unlike the ultrasonic approach, calculates , .=/,and

 from the E and G values and standard elasticity relationships whose uncertainties,

therefore, are ampliﬁed.

27.7 Conclusions

The ability to simultaneously measure a homogeneous, isotropic pipe’s elastic prop-

erties and wall thickness by using the cut-off frequencies of three ultrasonic guided

wave modes is demonstrated. Young’s modulus, the shear modulus, and wall thick-

ness agree very well with values found conventionally. Poisson’s ratios agree within

354 D.K. Stoyko et al.

assessed uncertainties. However, dimensional uncertainties cannot be reﬂected re-

alistically by the ultrasonic approach’s implicit assumption that dimensions do not

change along or around a pipe. On the other hand, conventionally found dimen-

sional uncertainties are more indicative of actual pipe variations as they are based

upon direct measurements.

Acknowledgments All three authors acknowledge the ﬁnancial support from the Natural Science

and E

ngineering Research Council (NSERC) of Canada. The ﬁrst author also wishes to acknowl-

edge ﬁnancial aid from the S

ociety of Automotive Engineers (SAE) International, University of

Manitoba, Province of Manitoba, Ms. A. Toporeck, and the U

niversity of Manitoba Students’

nion (UMSU). The assistance of Messrs. B. Forzley, I. Penner, D. Rossong, V. Stoyko and

Dr. S. Balakrishnan with preparation of the experimental sample is much appreciated. Recogni-

tion is given to Dr. M. Singh and Mr. A. Komus for the use and help with the load frame.

References

1. Alberta Energy and Utilities Board (1998) Pipeline performance in Alberta 1980–1997. Alta

Energy and Util Board, Calgary, AB

2. Alleyne D, Cawley P (1996) Excitation of Lamb waves in pipes using dry-coupled piezoelectric

transducers. J Nondestruct Eval 15:11–20

3. Alleyne D, Lowe M, Cawley P (1998) Reﬂection of guided waves from circumferential notches

in pipes. J Appl Mech, Trans ASME 65(3):635–641

4. Alleyne D, Pavlakovic B, Lowe M et al. (2001) Rapid, long range inspection of chemical plant

pipework using guided waves. In: Thompson D, Chimenti D, Poore L (eds) Review of progress

in quantitative nondestructive evaluation, vol 20. American Institute of Physics, Melville, NY,

pp 180–187

5. Buckingham E (1914) On physically similar systems: illustrations of the use of dimensional

equations. Phys Rev 4:345–376

6. Gazis D (1959) Three-dimensional investigation of propagation of waves in hollow circular

cylinders. J Acoust Soc Am 31(5):568–578

7. Hay T, Rose J (2002) Flexible PVDF comb transducers for excitation of axisymmetric guided

waves in pipe. Sens Actuators A (Phys) A100 (1):18–23

8. Krautkr¨amer J, Krautkr¨amer H (1977) Ultrasonic testing of materials, 2nd edn. Springer, Berlin

9. Liu G, Han, X (2003) Computational inverse techniques in nondestructive evaluation. CRC

Press, Boca Raton, FL

10. Lowe M, Alleyne D, Cawley P (1998) Mode conversion of a guided wave by a part-

circumferential notch in a pipe. J Appl Mech, Trans ASME 65(3):649–656

11. Mathworks, Incorporated, The (2008) Genetic algorithm and direct search toolbox

user’s guide. The Mathworks, Inc, Natick (http://www.mathworks.com/products/gads/

technicalliterature.html)

12. Moiseuev N, Friedland S (1980) Association of resonance states with the incomplete spectrum

of ﬁnite complex-scaled Hamiltonian matrices. Phys Rev A 22:618–624

13. Mu J, Zhang L, Rose J (2007) Defect circumferential sizing by using long range ultrasonic

guided wave focusing techniques in pipe. Nondestruct Test Eval 22(4):239–253

14. Rattanawangcharoen N (1993) Propagation and scattering of elastic waves in laminated circular

cylinders. Doctoral Dissertation, University of Manitoba

15. Rose J, Quarry M (1999) Feasibility of ultrasonic guided waves for non-destructive evaluation

of gas pipelines. Gas Research Institute, Chicago, IL

16. Silk M, Bainton K (1979) Propagation in metal tubing of ultrasonic wave modes equivalent to

Lamb waves. Ultrasonics 17:11–19

27 Inversely Found Elastic and Dimensional Properties 355

17. Stoyko D, Popplewell N, Shah A (2007) Modal analysis of transient ultrasonic guided waves

in a cylinder. In: Yao Z, Yuan M (eds) Computational Mechanics Proceedings ISCM 2007:

Abstract page 411, Full manuscript (pp 1215–1225) on accompanying CD-ROM, 211

FP-136-

PopplewellN.pdf Tsinghua University Press and Springer, Beijing

18. Stoyko D, Popplewell N, Shah A (2008) Feasibility of ﬁnding properties of homogeneous,

isotropic pipes using nondestructive guided waves. In: Brennan M (ed) Proceedings of the 7th

European conference structural dynamics: Abstract page 29, Full manuscript on accompanying

CD-ROM, E152.pdf Institute of Sound Vibration Research, Southampton, Hampshire

19. Stoyko D, Popplewell N, Shah A (2009) Ultrasonic measurement of dimensional and material

properties. In: Thompson D, Chimenti D (eds) Review of progress in quantitative nondestruc-

tive evaluation, AIP Conference Proceedings 1096. American Institute of Physics, Melville,

NY, pp 1267–1274

20. Wilkinson J (1965) The algebraic eigenvalue problem. Oxford University Press, Oxford

21. Zhuang W, Shah A, Dong S (1999) Elastodynamic Green’s function for laminated anisotropic

circular cylinders. J Appl Mech 66:665–674

Chapter 28

Nonlinear Self-Deﬁned Truss Element Based

on the Plane Truss Structure with Flexible

Connector

Yajun Luo, Xinong Zhang, and Minglong Xu

Abstract A ﬁnite-element method based on the self-deﬁned truss element is

developed and used to model the plane truss structure with the ﬂexible connector,

moreover, the dynamic characteristic of the corresponding model is analyzed in

this paper. Firstly, a kind of new type truss structure is analyzed where the ﬂexible

connectors between trusses include clearance effects. A self-deﬁned truss element

is deﬁned based on the mechanical analysis and then used to build the ﬁnite-element

model. And the nonlinear elastic-damper model and the Coulomb friction model are

adopted to analyze the nonlinear nodal forces from the clearance ﬁeld. Secondly, a

nonlinear numerical solution method is developed based on the Newmark implicit

integrate method together with Newton–Raphson iterated method and then used to

solve the nonlinear dynamic model. Finally a numerical example is performed by

the method above and the effects of several key parameters (such as the contact

stiffness and the clearance) on the dynamic characteristic are analyzed. The results

validate the numerical solution method and show that the nonlinear ﬁnite-element

model is effective.

28.1 Introduction

Presently, various connectors are wildly adopted in the modern space structure such

as the deployable antenna and the solar plate for the requirement of the launching,

deformation, and attitude control. The dynamic analyses of the connectors are usu-

ally primary and key in the full structural analyses. Moreover, the connectors will

result in variety and complexity of the dynamic analysis of the space structure.

Common connectors, such as the spherical joint [1] and the sleeve connector [2]

in the deployable structure and the pre-load connector in the truss structure [3], gen-

erally include clearance, friction, impact, and other nonlinear cases. Furthermore,

X. Zhang (



)

School of Aerospace, Xi’an Jiaotong University, Xi’an 710049, People’s Republic of China

e-mail: xnzhang@mail.xjtu.edu.cn

A.C.J. Luo (ed.), Dynamical Systems: Discontinuity, Stochasticity and Time-Delay,

DOI 10.1007/978-1-4419-5754-2

28,

 Springer Science+Business Media, LLC 2010

357

358 Y. L u o e t a l .

the errors induced by manufacturing and assembling usually also result in the

randomness of the structural parameters in the practical structure. Therefore, the

modeling of the connectors is not easy for the complicated cases above. At present,

main reports such as the 3-D spherical joint model [1], the sleeve-type connec-

tor model considering the Coulomb friction and clearance effect [2, 4], the bilin-

ear hysteresis model [3, 5], are contributive to the development of this ﬁeld. The

other work for the connectors, for instance, Flores et al. [6] studied the nonlinear

dynamical behavior of the translational joints with clearance, Shi and Atluri [7]

used the Ramberg–Osgood function to describe the nonlinear elastic performance,

and Gaul and Lenz [8] used the Valanis model to analyze the slip and adhesion

characteristic of the contact ﬁeld, make also contribution to the design and applica-

tion of the connectors and other clearance mechanisms. Conclusively, the clearance

effect is still the main research focus because it widely exists in the connectors

and easily results in the impact and friction effect. The friction models include the

Coulomb friction model, LuGre friction model, and so on. The impact models are

mainly classiﬁed into two types, one is the linear impact model [9] and the other is

the nonlinear elastic-damper model [10–12]. The two models are put forward based

on Hertz contact theory, but the damping forces are considered based on the dif-

ferent hypothesizes. Generally, the latter is employed because it is closer to actual

case than the former. However, with the development of the modern space structure

technology, many new connectors which are with better performance and can sat-

isfy more special requirements are being designed, so some new modeling methods

need to be developed now.

Truss structure is still used widely in the space structure. The connectors be-

tween the truss and the main body structure, or between the truss and the support

structure, or among the trusses have various construction for different application

forms. The truss structure with the ﬂexible connectors which belong to the slideable

connector is applied in a space structure for satisfying some special requirements in

this study. Firstly, a self-deﬁned truss element which has considered the clearance

effect is deﬁned based on the construction of the ﬂexible connector. The nonlinear

elastic-damper model and Column friction model are adopted here. Secondly, the

nonlinear dynamic equations of the full system are obtained. Finally, the nonlinear

dynamic equations are solved in the time domain using the Newmark method for

time integration, in which the Newton–Raphson method is used for handling the

non-linear behavior within each time step. Furthermore, the dynamic characteristic

and response are analyzed by the numerical simulation. And the dynamic effects of

some key parameters on the full system are also analyzed.

In summary, the dynamic modeling based on the self-deﬁned truss and the cor-

responding nonlinear numerical solution method are explored. Moreover, they are

shown as effective approaches for the dynamic analysis of a new type truss structure

with the ﬂexible connector.

28 Nonlinear Self-Deﬁned Truss Element Based on the Plane Truss Structure 359

28.2 Finite-Element Dynamic Modeling

28.2.1 Introduction of the Structure

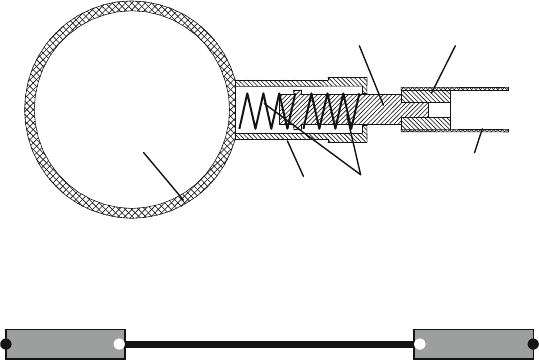
The ﬂexible truss structure is shown in Fig. 28.1. The ﬂexible connector consists

of six parts: a hollow sphere, a sleeve, two linked springs, a linkage, an inserted

nut, and a hollow rod. The hollow sphere is used as the joint to connect the adja-

cent trusses. The sleeve is used to connect the hollow sphere and the hollow rod, in

which is embedded two linked spring and a linkage. One end of the sleeve is welded

with the hollow sphere. The outer ends of the two linked springs are pressed on the

right end and the left end of the sleeve by a pre-load, respectively. The truncated

cone which locates in the middle of the linkage is used to separate the two adjacent

springs. It is likely to contact with the sleeve during the motion. The inserted nuts

in the ends of the hollow rod are designed because the hollow rod is a thin wall

structure and is hard to be directly connected with other components. They can re-

alize the threaded connection between the linkages and the hollow rods. Obviously,

the ﬂexibility of the connector and the full truss structure is depended on the stiff-

ness of the linked spring based on the design of this ﬂexible connector. That is, the

truss structure with various ﬂexibilities can be obtained by assembling the linked

springs with different stiffness levels. It is just a highlight of this connector. More-

over, the clearance between the sleeve and linkage is considered in the model as

showninFig.28.1. Compared with the traditional truss structure, the ﬂexible truss

structure is with more complex nonlinearity and modeling hardness.

The diagram of the self-deﬁned truss element used to simulate the ﬂexible truss

in the ﬁnite-element model is shown in Fig. 28.2. One truss is modeled as one

sleeve

linked spring

hollow sphere

inserted nutlinkage

hollow rod

Fig. 28.1 The construction of the ﬂexible connector

Fig. 28.2 The model of the self-deﬁned truss element

360 Y. L u o e t a l .

self-deﬁned truss element with three sub-elements. The sub-element E1, E3, and E2

in the self-deﬁned element are used to describe the left and right ﬂexible connection

and the middle hollow rod, respectively. The node i and p are located at the center

of the hollow spheres, respectively. The node j and q are located approximately at

the two ends of the hollow rods.

28.2.2 Motion Equations of the Self-Deﬁned Truss Element

There are two contact pairs: one is located between the linkage and the right end

of the sleeve (the contact pair a); the other is located between the sleeve and the

truncated cone of the linkage (the contact pair b). The point contact can be assumed

because the area of the contact surface is very small. Both the contact forces and the

friction forces at the two contact pairs are considered. The stiffness of the sleeve and

the linkage is much larger than that of the linked spring so they are assumed as rigid

body and only the inertia is considered. Through the force analysis, the equilibrium

equations of the connector can be written as follows:

gCC

gCK

gDfF

g; (28.1)

where M

, C

, K

,andfF

g are the mass matrix, damping matrix, stiffness

matrix, and load vector, respectively.

The sub-element E3 and E1 are located symmetrically along the axial direc-

tion. The material, size, force analysis, and boundary conditions of the sub-element

E3 are the same as those of the sub-element E1. So its motion equations can be

directly obtained. For the sub-element E2, the traditional plane frame element is

adopted here.

Finally, the motion equations of the self-deﬁned element can be obtained by

the superposition of all the dynamic matrix and vectors along the direction of the

corresponding coordinates according to the ﬁnite-element assembly method. The

ﬁnite-element equations have been given as follows.

gCC

gCK

gDfF

g (28.2)

To expand the load vector fF

g, it can be written as below:

gDfF

gCfF

g; (28.3)

where fF

g and fF

g are the load vectors about the clearance effect and the nodal

load, respectively. In order to analyze the numerical solution method of the nonlinear

motion equations conveniently, the summary nodal force is deﬁned as,

gDK

gfF

g (28.4)

28 Nonlinear Self-Deﬁned Truss Element Based on the Plane Truss Structure 361

and then the motion equations of the self-deﬁned element can be revised as

gCC

gCfR

gDfF

g; (28.5)

where the external load vector fF

g is equal to fF

28.3 Nonlinear Nodal Forces

Based on the nonlinear elastic-damper model [12], the contact force at every contact

pair is the sum of the elastic restoring force and the damping restoring force. For

example, at the contact pair a,

D F

C F

; (28.6)

where the expression of the elastic restoring force F

and the damping restoring

force F

are written as follows, respectively.

D K

h."

/ (28.7)

D C

h."

/; (28.8)

where n is a factor. h."

/ is a Heaviside function used to describe the direction of

the contact force. "

is the relative displacement of the middle of the contact pair a.

Similarly, the contact force of the contact pair b can also be obtained.

In the Coulomb friction model, the friction forces F

at the contact pair a are

expressed as:

D F

sign. Px

Px

/ D .K

h."

/CC

h."

//sign. Px

Px

/; (28.9)

where  is the friction factor and the function sign(x) is used to describe the direc-

tion of the friction force.

By substituting the concrete expressions of the contact force and friction force

into the contact load vector fF

g, the nonlinear nodal force vector of the local ele-

ment can be obtained. Furthermore, the tangent stiffness matrix of the nodal force

vector of the self-deﬁned element in the local coordinate can be derived from (28.4).

@fR

@fu

@.K

gfF

@fu

D K



@fF

@fu

; (28.10)

where the expressions of every elements in the tangent stiffness matrix and the

contact stiffness matrix can be written as

.i; j / D K

.i; j /  K

.i; j /; i; j D 1; 2; 3; 4; 5; 6 (28.11)

362 Y. L u o e t a l .

.i; j / D

@fF

.i/g

@fu

.j /g

;i;jD 1; 2; 3; 4; 5; 6; (28.12)

where K

and K

are the elastic stiffness matrix and the contact stiffness matrix,

respectively.

28.4 The Numerical Solution Method and Example

28.4.1 The Numerical Solution Method

In this search, the Newmark implicit integral method is employed for time integra-

tion, and then the Newton–Raphson method is employed for equilibrium iteration

in each time step. Therefore, the equation can be written as the following iterative

form.

nC1

gCC

nC1

k1

f

gDf

nC1

gf

nC1

k1

g (28.13)

where

f

gDf

nC1

gf

nC1

k1

g (28.14)

Then, (28.4)and(28.10) can be modiﬁed as

nC1

k1

gDfR

nC1

k1

g/gDK

nC1

k1

gfF

nC1

k1

g/g (28.15)

nC1

k1

D K

nC1

k1

g/ D K

 K

nC1

k1

g/ (28.16)

Equations (28.15)and(28.16) are substituted into (28.13), then

nC1

gCC

nC1

gCŒK

 K

nC1

k1

g/f

gDf

nC1

gK

nC1

k1

CfF

nC1

k1

g/g

(28.17)

Equation (28.17) is just the iteration formula of the self-deﬁned element at the

time t

nC1

28.4.2 Numerical Example

A truss structure with only one ﬂexible truss is considered in the numerical example.

Its structural diagram is given as shown in Fig. 28.3. Both the left and right ends

are ﬁxed. A transverse force F

and an axial force F

are simultaneously applied at

the node 2. The responses of both node 2 and node 3 along all DOF directions can

be excited under these loading conditions. As shown in Fig. 28.4, the length of the

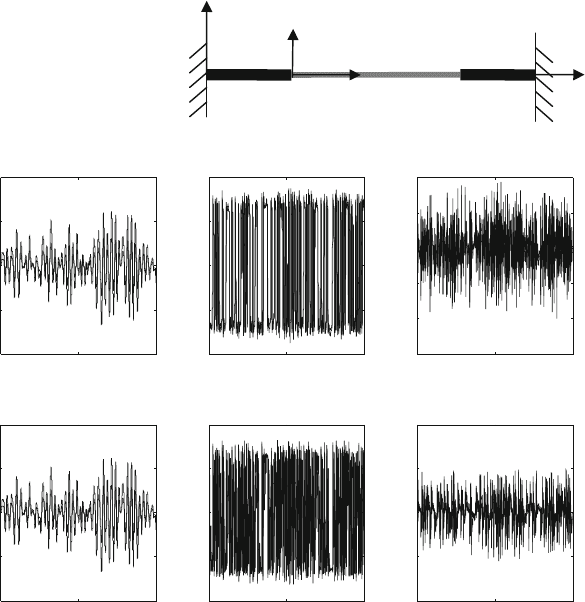
28 Nonlinear Self-Deﬁned Truss Element Based on the Plane Truss Structure 363

Fig. 28.3 The construction

of the single ﬂexible truss

structure

0 0.5 1

−0.01

−0.005

0.005

0.01

Time (s)

Displacement (m)

0 0.5 1

−2

−1

x 10

-4

Time (s)

Displacement (m)

0 0.5 1

−3

−2

−1

x 10

-3

Time (s)

Angle (rad)

0 0.5 1

−0.01

−0.005

0.005

0.01

Time (s)

Displacement (m)

0 0.5 1

−2

−1

x 10

-4

Time (s)

Displacement (m)

0 0.5 1

−4

−2

x 10

-3

Time (s)

Angle (rad)

def

Fig. 28.4 The displacement response curves. (Node 2: (a)X;(b)Y;(c) ™ Node 3: (d)X;(e)Y;

(f) ™ Factor of random excitation: solid line 0.25; dashed line 0.5)

truss is 0.42 m, the length of the connector is 0.051 m, the stiffness of the linkage

spring is 1,580 N/m, and all the parts are made of steel.

28.4.2.1 Random Excitation

A group random signal with 0–100 Hz frequency range is adopted as the excited

force by the gain ampliﬁer. The different excited force levels are adopted because

the stiffness level along the axis direction is signiﬁcant difference compared with

that of the transverse direction. In this example, the corresponding gain factors of

and F

are 0.25 and 1:25, respectively. Simultaneously, the gain factors of F

and F

are increased twice and changed as 0.5 and 2:5 in order to compare the

effects of the different levels of the excited force. The clearance value is 127 min

the connector.