Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay
Подождите немного. Документ загружается.


374 L.-F. L¨uetal.
29.3 Construction of Green’s Function
G.xI/ should satisfy the equation according to the definition of the Green’s
function, as
.
2
C/G.xI/C.2c Cc/G
0
.xI/C.c
2
1/G
00
.xI/ D ı.x / (29.8)
and boundary condition
G.0I/ D G.1I/ D 0: (29.9)
Generally, (29.8) with (29.9) can be solved by taking advantage of properties of
the Green’s function, e.g., the continuous condition and jump condition at x D .
The tedious procedure can be eliminated by using the construction of Green’s
theorem [9], which permits explicit expression of the Green’s function, as follows.
For the second linear differential operator L D P.x/d
2
=dx
2
C Q.x/d=dx C
R.x/,ifu
1
.x/ and u
2
.x/ satisfy
Lu
1
D 0; au
1
.
0
/ C a
0
u
0
1
.
0
/ D 0;
(29.10)
Lu
2
D 0; bu
2
.
1
/ C b
0
u
0
2
.
1
/ D 0
and W.u
1
; u
2
/ ¤ 0, then the Green’s function for L can be expressed as
G.xI/ D
1
P./W.u
1
; u
2
/
ˇ
ˇ
xD
(
u
1
.x/u
2
./; x <
u
1
./u
2
.x/; < x
; (29.11)
where
0
;
1
are two boundaries and W.u
1
; u
2
/ is the Wronskian determination de-
fined as
W.u
1
; u
2
/ ,
ˇ
ˇ
ˇ
ˇ
u
1
.x/; u
2
.x/
u
0
1
.x/; u
0
2
.x/
ˇ
ˇ
ˇ
ˇ
: (29.12)
With the following fundamental properties of the Green’s function, it is easy to
verify that the expression given by (29.11) is the Green’s function. That is to say
that G.xI/ is continuous
G.xI
/ D G.xI
C
/ (29.13)
and the derivative dG=dx satisfies the jump condition at x D
dG
dx
ˇ
ˇ
ˇ
ˇ
C
dG
dx
ˇ
ˇ
ˇ
ˇ
D
1
P.x/
: (29.14)
There are two independent solutions to the homogeneous differential (29.8)which
satisfy each of the boundary conditions given by (29.9)
(
1
.x/ D exp.
x/ exp.
C
x/; 0 x
2
.x/ D exp.
.x 1// exp.
C
.x 1//; x 1
; (29.15)

29 Complex Frequency Analysis of an Axially Moving String 375
where
˙
D
.2c C c/ ˙
p
2
c
2
C 4
2
C 4
2.c
2
1/
:
By applying the above-mentioned method, one can get
G.xI/ D
1
.c
2
1/W .
1
;
2
/
ˇ
ˇ
xD
(
1
.x/
2
./; 0 x
1
./
2
.x/; x 1
; (29.16)
where W.
1
;
2
/ ¤ 0 holds. Substitution of (29.16)into(29.7) leads to the frequen-
cies. In order to solve this equation, the eigenvalue of the unconstrained system is
adopted as an initial solution
m
i
D I
p
k
i
=m
i
;
n
str
D ˙ I!
n
;
D
1
2
; !
n
D
1
2
p
.c
2
1/.
2
C 4
2
n
2
.c
2
1//; I D
p
1: (29.17)
Particularly, for a conservative system, the initial eigenvalues of the string alone are
str
n
D n.1 c
2
/I; n D˙1; ˙ 2;::: (29.18)
It is worth pointing out that there exists a singularity in the Green’s function, i.e.,
c D 1, which is the critical speed of the system and corresponds to a non-oscillatory
eigenvector .x/ D 0.
29.4 Results and Discussions
The numerical examples presented hereafter aim to examine the effect of one or
several attached mass-spring oscillators on the eigenvalues of an axially moving
string, especially when the eigen-frequency of the oscillator is close to the first
eigen-frequency of the translating string.
For the problem of a single oscillator, the parameters c D 0:25; k D 3:4,and
m D 0:375 are assigned. The eigenvalues of a conservative system (i.e., D 0)
and a dissipative system with D 0:04 are shown in Figs. 29.2 and 29.3, respec-
tively, both varying with the location of the oscillator x
0
. The eigenvalues of the
coupled system derived from the eigenvalues of unconstrained string and oscillator
are marked by solid lines and dot-dashed lines, respectively. When c<1, the con-
servative system is positive definite and gyroscopic, thus only imaginary eigenvalues
exist [10]. It is noted that both the real and imaginary parts of the eigenvalues of the
constrained system are symmetric with respect to x
0
D 0:5 due to the symmetry of
the Green’s function. The distributions of the eigen-frequencies (the imaginary part
of the eigenvalues) of the constrained system are in accordance with the principle of
eigenvalue inclusion [11], which applies only for conservative gyroscopic system.
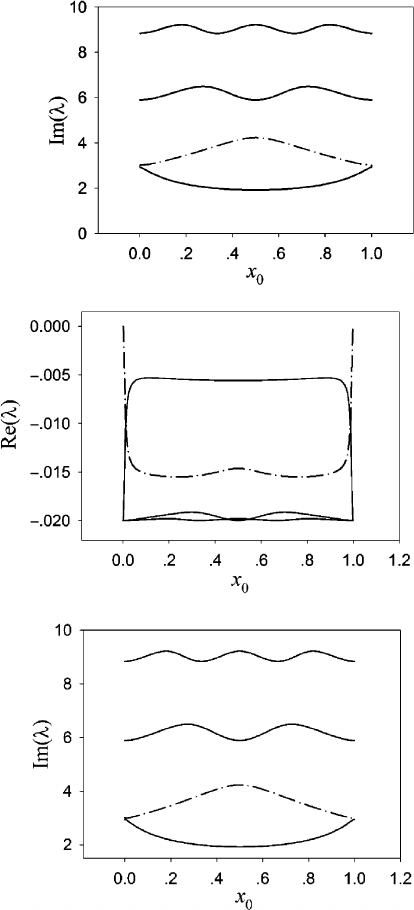
376 L.-F. L¨uetal.
Fig. 29.2 The first four
eigenvalues of the single
moving oscillator model
with D 0
Fig. 29.3 The first four
eigenvalues of the single
moving oscillator model
with D 0:04
As shown in Fig. 29.3a, it is not the case that the distributions of the real part of the
eigenvalues of the constrained system have the similar principle.
With the above assigned parameters the eigen-frequencyof the attached oscillator
.!
m
D 3:0111/ is very close to the first natural frequency of the unconstrained

29 Complex Frequency Analysis of an Axially Moving String 377
Table 29.1 The maximum variance rate of the eigen-frequencies of the coupled system
Im.
1
str
/
(%)
Im.
2
str
/
(%)
Im.
3
str
/
(%)
Im.
m
1
/
(%)
Im.
m
2
/
(%)
Single-oscillator model 34.99 10.01 4.32 41.43
Double-oscillator model 39.16 12.27 6.73 63.61 20.35
Double-mass model 34.23 22.53 19.49
moving string. Therefore, both the real and the imaginary part of the first eigen-
value of the constrained string change significantly with the varying attached
oscillator, which is related to the resonance-type of the eigenvalue. Other eigen-
values have also changed but not significantly. In order to determine the coupling
strength of the subsystems quantitatively, the maximum variance rate defined by
˛
i
D sup
ˇ
ˇ
Im
u
i
c
i
ˇ
ˇ
ı
min
Im
u
i
; Im
c
i
;i D 1; 2;::: is used, where
u
i
and
c
i
represent the ith eigenvalues of the unconstrained system and the con-
strained system, respectively. The maximum variance rate is tabulated in Table 29.1.
It can be seen that the variance rate of the eigen-frequencies of the moving string
drops with the increasing order of the modes. Moreover, the effect of higher modes
is relatively small on low-frequency response. This implies that the transient solu-
tions of the coupled system can be approximated by using the expansion of first few
modes of the system.
For the eigenvalue problem of an axially moving string with two mass-
spring oscillators, an equal stiffness of spring k
1
D k
2
D k and different
masses m
1
and m
2
are used. In this case, the parameters are chosen to be
m
1
D0:375; m
2
D0:3; t
1
D 0; t D 1 and t
2
D t
1
C t. The whole process of
movement can be divided into three parts
I W t 2 Œ0; t ; „
1
D 1; „
2
D 0; x
1
D ct;x
2
D 0;
II W t 2 Œt; 1=c ; „
1
D 1; „
2
D 1; x
1
D ct;x
2
D c.t t/;
III W t 2 Œ1=c; t C 1=c ; „
1
D 0; „
2
D 1; x
1
D 0; x
2
D c.t t/:
As shown in Fig. 29.4, the eigenvalue curves are no longer symmetric with respect to
the central point .t D 2:5/ on the time axis due to different masses of the oscillators.
Nonetheless, the eigenvalue curves will be mirrored about t D 2:5 as a result of the
symmetry of the Green’s function if the two masses are interchanged. For Parts
I and III, the eigenvalues are identical to those of the first and second oscillators
individually placed on the string, whereas for Part II another additional eigenvalue
appears when the second oscillator steps in, with less variance of frequency than
that of the first one. The maximum variance rate of other eigenvalues resembles the
one from the problem of single oscillator, though it becomes larger in magnitude.
Strictly speaking, the limit case of moving oscillators will be the one with in-
finitely large spring stiffness, which is not equivalent to the problem of moving
mass problem [12]. However, (29.7) is still valid for the eigenvalue problem of
coupled systems with attached masses since there is no additional assumption but
"
i
D m
i
2
. The variance of the first three eigenvalues of attached two masses model
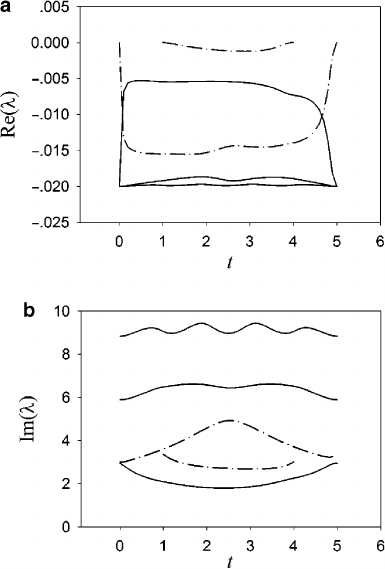
378 L.-F. L¨uetal.
Fig. 29.4 The first three
eigenvalues of multiple two
oscillators model
is depicted in Fig. 29.5 with c D 0:25; D 0:04; m
1
D 0:375,andm
2
D 0:3.The
maximum variance rate of the first three eigenvalues is also listed in Table 29.1.
Compared to the model of attached oscillator, the effect of moving mass on the first
three eigenvalues of the string are significant. This means that the transient solutions
of the coupled mass-string system should be approximated using much more modal
expansions of the system than that of the attached oscillator system.
It should be noted that the eigenvalue problem from (29.7) will be complicated
for very large N . The Galerkin’s discretization method is used to approximately
approach the eigenvalue solutions of (29.7), for which the eigen-functions of the
stationary string
n
D sin.nx/ are chosen. The Jacobian coefficient matrix of dis-
crete ODEs is shown in the Appendix. The first two eigen-frequencies of moving
string under double oscillators with the parameters above are computed for different
orders of expansion: M D 4; 8; 16, respectively, at various moments in Table 29.2.
It can be seen that the Galerkin’s method can capture the dynamical characteris-
tics of the string when locations of the oscillators vary. The results are more and
more accurate with increasing orders of expansion in comparison with the calcu-
lations of determination (29.7). Although it has been demonstrated that Galerkin’s
discretization method using Fourier series expansion can be effective to analyze the
dynamics of the moving systems, the expansion is still questionable for insufficient
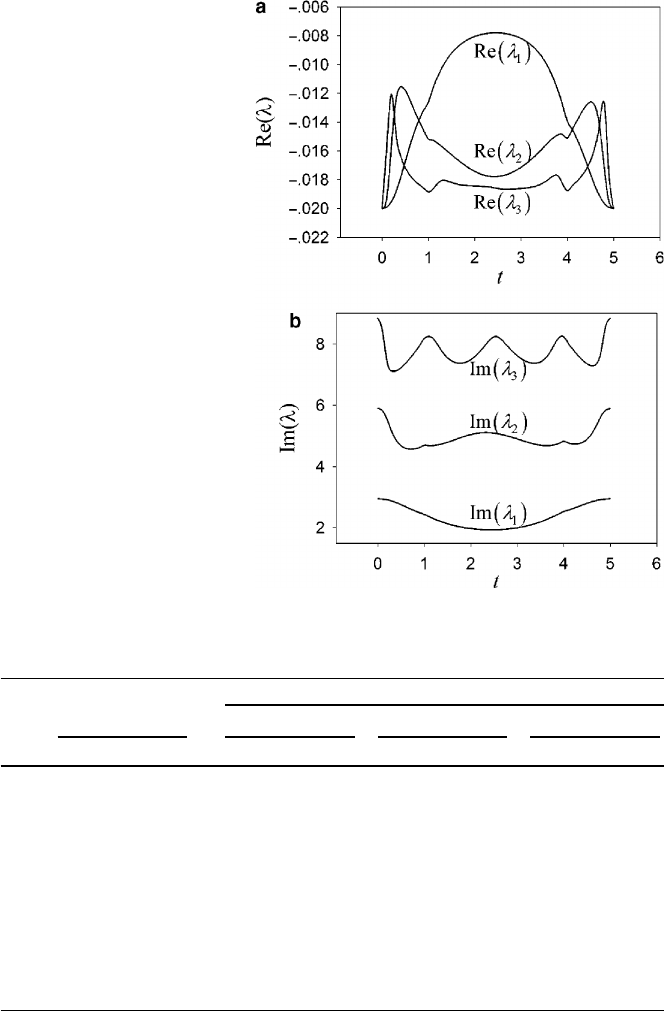
29 Complex Frequency Analysis of an Axially Moving String 379
Fig. 29.5 The first three
eigenvalues of the moving
masses model
Table 29.2 Comparison of the first two eigen-frequencies of moving string under double
oscillators between Galerkin’s discretization method of different order of expansion with the
present paper
Galerkin’s discretization method
The present paper M D 4MD 8MD 16
t Im.
1
str
/ Im.
2
str
/ Im.
1
str
/ Im.
2
str
/ Im.
1
str
/ Im.
2
str
/ Im.
1
str
/ Im.
2
str
/
0 2.9452 5.8905 2.9461 5.9023 2.9453 5.8918 2.9452 5.8906
0.5 2.3667 6.1510 2.4109 6.1777 2.3907 6.1632 2.3789 6.1568
1.0 2.0876 6.4804 2.1211 6.5547 2.1042 6.5117 2.0959 6.4947
1.5 1.9162 6.6021 1.9379 6.7000 1.9292 6.6448 1.9226 6.6223
2.0 1.8152 6.5723 1.8343 6.6618 1.8259 6.6168 1.8205 6.5922
2.5 1.7938 6.4340 1.8116 6.5172 1.8041 6.4596 1.7988 6.4465
3.0 1.8541 6.5381 1.8727 6.6218 1.8648 6.5798 1.8594 6.5567
3.5 2.0149 6.6127 2.0369 6.7144 2.0274 6.6569 2.0210 6.6337
4.0 2.2528 6.5137 2.2822 6.5942 2.2672 6.5478 2.2601 6.5293
4.5 2.5472 6.1662 2.5807 6.1951 2.5657 6.1797 2.5566 6.1727
5.0 2.9452 5.8905 2.9461 5.9023 2.9453 5.8918 2.9452 5.8906
380 L.-F. L¨uetal.
theoretical foundation. From the eigenvalue point of view, with the Galerkin’s
discretization method, the transient responses of the moving string with attached
oscillators will be more and more reliable with increasing orders of expansion.
29.5 Conclusion
The eigenvalue problem of an axially moving string coupled with multiple linear
oscillators is investigated by Green’s function method. The Green’s function in
an explicit form is obtained by the theorem of Green’s function construction, and
the analytical transcendental equation is directly obtained. The numerical examples
show that both the real and the imaginary parts of eigenvalues are varying. The
maximum variance rate is defined to analyze the coupling strength of the subsys-
tems. It is demonstrated that only the first eigenvalue changes significantly when
the eigen-frequency of the oscillator is close to that of the string’s first eigenvalue,
while all the eigen-frequencies of the string are significantly influenced by the mov-
ing mass model. Furthermore, the validity of the Galerkin’s method is presented for
a number of oscillators, which can be used to approximately solve the eigenvalue
problem without complicated computations of the determinant equation.
Acknowledgement The authors are grateful to the Natural Science Foundation of China (Project
10721062) and to the National 863 (Project 2007AA04Z405) for their fundings.
Appendix
The Jacobian matrix of the discrete ordinary differential equations of the moving
string with multiple linear mass-spring oscillators
8
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
<
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
:
J.2i 1; 2i / D 1; 1 i M C 2
J.2i;2j 1/ D.i /
2
.1 c
2
/ 2
N
P
nD1
k
n
2
i
.x
n
/; J.2i; 2j / D; 1 i D j M
J.2i;2j 1/ D2cd
ij
2
N
P
nD1
k
n
i
.x
n
/
j
.x
n
/; J.2i; 2j / D4cd
ij
;1 i ¤ j M
J.2i;2.M C n/ C 1/ D 2k
n
i
.x
n
/; 1 i M C 2
J.2.M C n/; 2j 1/ D k
n
=m
n
j
.x
n
/; 1 n N; 1 j M
J.2.M C n/; 2.M C n/ 1/ Dk
n
=m
n
;1 n N
J.i;j/ D 0; for other i;j
where d
ij
D ij.1 .1/
iCj
/=.i
2
j
2
/.
29 Complex Frequency Analysis of an Axially Moving String 381
References
1. Meirovitch L (1974) A new method of solution of the eigenvalue problem for gyroscopic
systems. AIAA J 12(10):1337–1342
2. Meirovitch L (1975) A modal analysis for the response of linear gyroscopic systems. J Appl
Mech 42:446–450
3. Parker RG (1998) On the eigenvalues and critical speed stability of gyroscopic continua. J Appl
Mech 65:134–140
4. Wang YF, Huang LH, Liu XT (2005) Eigenvalue and stability analysis for transverse vibrations
of axially moving strings based on Hamiltonian dynamics [J]. Acta Mech Sin 21(5):485–494
5. Stanisic MM (1985) On a new theory of the dynamic behavior of the structures carrying moving
masses. Arch Appl Mech 55(3):176–185
6. Kukla S (1991) The Green function method in frequency analysis of a beam with intermediate
elastic supports. J Sound Vib 149(1):154–159
7. Kukla S, Zamojska I (2007) Frequency analysis of axially loaded stepped beams by Green’s
function method. J Sound Vib 300:1034–1041
8. Pesterev AV, Yang B, Bergman LA (2001) Response of elastic continuum carrying multiple
moving oscillators. J Eng Mech 127(3):260–265
9. Gerlach UH (2007) Linear mathematics in infinite dimensions: signals, boundary value prob-
lems, and special functions. Lecture Notes of Ohio State University, http://www.math.ohio-
state.edu/gerlach/math/BVtypset/
10. Lee KY, Renshaw AA (2000) Solution of the moving mass problem using complex eigenfunc-
tion expansions. J Appl Mech 67:823–827
11. Yang B (1992) Eigenvalue inclusion principles for distributed gyroscopic systems. J Appl Mech
59:650–656
12. Pesterev AV, Bergman LA, Tan CA, Tsao TC, Yang B (2003) On asymptotics of the solution
of the moving oscillator problem. J Sound Vib 260:519–536

Chapter 30
Model Reduction on Inertial Manifolds
of Navier–Stokes Equations Through
Multi-scale Finite Element
Jia-Zhong Zhang, Sheng Ren, and Guan-Hua Mei
Abstract Multilevel finite element method is used to approach the Approximate
Inertial Manifolds (AIMs) from viewpoint of nonlinear dynamics, in the compu-
tational fluid dynamics. By this method, an unknown variable is divided into two
components, namely, the large eddy and small eddy components. With the introduc-
tion of an AIMs, the interaction between large eddy and small eddy components,
which is negligible if standard Galerkin algorithm is used to approach the original
governing equations, is considered essentially, and consequently a coarse grid finite
element space and a fine grid incremental finite element space are introduced to ap-
proach the two components. By this method, the flow field of incompressible flows
around airfoil is simulated numerically as an example, and velocity and pressure
distributions of the flow field are obtained accurately. The results show that there
exists less degrees-of-freedom in the discretized system in comparison with the tra-
ditional methods, and large computing time can be saved by this efficient method.
The small eddy component can be captured by AIMs, and an accurate result can
also be obtained.
30.1 Introduction
Most of dynamic systems encountered in engineering are nonlinear continuous
dynamic systems, which have a rich variety of nonlinear dynamical phenomena,
such as the large and complex fluid-structure interaction systems. Normally, the
finite element method or other numerical methods are used to approach the solu-
tions of the governing equations, due to the difficulty of obtaining a solution in
analytical form. As the results, the resulting equations are generally second order
in time dissipative evolution equations with many degrees-of-freedom in sense of
J.-Z. Zhang (
)
School of Energy and Power Engineering, Xi’an Jiaotong University,
No. 28, Xianning West Road, Xi’an, Shaanxi 710049, People’s Republic of China
e-mail: jzzhang@mail.xjtu.edu.cn
A.C.J. Luo (ed.), Dynamical Systems: Discontinuity, Stochasticity and Time-Delay,
DOI 10.1007/978-1-4419-5754-2
30,
c
Springer Science+Business Media, LLC 2010
383
384 J.-Z. Zhang et al.
dynamics. For such kind of equations, there are several classical numerical schemes
to approximate them, such as Newmark, Wilson-, Houbolt, and the Runge–Kutta
scheme with higher precision if the system is transferred into phase space. However,
great difficulties will arise from analyzing the nonlinear dynamics both qualita-
tively and quantitatively in a finite dimensional phase space of higher dimension
[1]. For example, the analysis of nonlinear dynamical systems, based on the nu-
merical schemes mentioned above, requires considerable computing time due to the
large number of degrees-of-freedom, and some numerical round-off errors will have
a strong influence on the long-term behaviors of the systems or the bifurcation anal-
ysis if the systems have a cluster of bifurcation points [2–5]. In other words, model
reduction is the key to such obstacle and currently urgent for the bifurcation analysis
by large scale numerical computation. Therefore, it is natural to reduce the model
from higher to lower dimensions and to achieve an acceptable approximation of the
original dynamics before large-scale numerical analysis is applied to the original
system. Indeed, this reduction technique can be reached for some certain dissipative
systems, by neglecting inessential degrees-of-freedom of the system and keeping
the topology of the solutions unchanged [1]. Under such background, a number of
researchers have developed many practical numerical algorithms [2]. For the linear
dynamic system, the component mode synthesis techniques can be used to ana-
lyze the dynamic behaviors of the system, and much computing time will be saved,
and an approximate result can be acceptable. However, for the nonlinear dynamic
system, there are a few methods for the model reduction. Most of the numerical al-
gorithms are developed based on the component mode synthesis techniques, which
can be used for linear dynamical systems with acceptable approximate results, while
few rigorous theoretical studies or the error estimate has been carried out on the in-
fluence of such reduction on the long-term behaviors, though a lot of numerical
experiments are given [6–10]. Strictly speaking, due to the strong nonlinearities of
some dissipative autonomous dynamical systems, the reduction of the systems has
a greater influence on the solution at a certain degree, in a mathematically precise
way [11,12].
Fluid dynamics, a kind of continuous dynamic system, is governed by a set of
nonlinear dissipative evolutionary equations, and there are many nonlinear phenom-
ena, such as separation in boundary layer, soliton and turbulence, and some other
open problems in it. In particular, the connections between fluid mechanics, partial
differential equations and nonlinear dynamical system, and the global attractors and
turbulence, are the essential heart of understanding of many important problems of
natural science. There are a number of numerical analysis of Navier–Stokes equa-
tions based on Finite Element Method, and most of them are the adaptations of
traditional Galerkin procedure [1]. However, an important deficiency of the existing
numerical methods in the computation fluid dynamics is the cost of computing-
time, that is, there are a large number of degrees-of-freedom after the system is
approached by the discretization, and the system is the one with higher dimension
from viewpoint of nonlinear dynamics. Hence, in the nonlinear continuous dynamic
systems, it is the current aim to reduce the original system to a system with less
degrees-of-freedom.
