Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay

Подождите немного. Документ загружается.

364 Y. L u o e t a l .

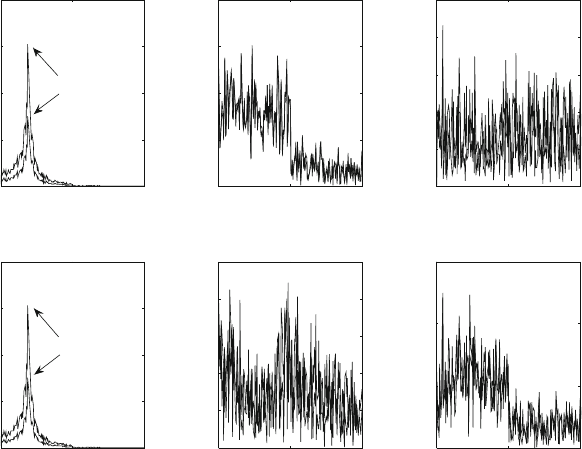
The displacement responses of the nodes 2 and 3 are given as shown in Fig. 28.4.

The responses along the transverse and rotation directions are mostly constrained

by the clearance. However, the responses along the axial direction are obviously

different under two kinds of excitation. It is found that the excited force with greater

amplitude generates the response with greater level. The nonlinearity along the axial

direction is not strong though the friction effect has been considered. And the axial

displacements at nodes 2 and 3 are almost synchronous as shown in Fig. 28.4a, d. It

is the cause that the axial stiffness of the hollow rod between the two nodes is much

larger than that of the connectors.

The conclusions above are also explained from Fig. 28.5 wherein the correspond-

ing displacement spectrum curves are given. It is indicated that the ﬁrst frequency

is 38.0 Hz in Fig. 28.5a, d. And it is found that the curves are much unorganized for

the signiﬁcant nonlinearity from the other four sub-ﬁgures.

The position curves at the two nodes with clearance are given in Fig. 28.6 in

order to observe the contact motion law along the transverse direction. The two

boundaries just express the value of the clearance. If the positions are between the

up and below boundaries, it expresses no contact, otherwise contact. The excess

parts of the positions compared with two boundaries are just the penetration of the

0 100 200

Frequency (Hz)

Spectrum (m)

0 100 200

0.1

0.2

0.3

0.4

Frequency (Hz)

Spectrum (m)

0 100 200

0.2

0.4

0.6

0.8

Frequency (Hz)

Spectrum (rad)

0 100 200

Frequency (Hz)

Spectrum (m)

0 100 200

0.05

0.1

0.15

0.2

0.25

Frequency (Hz)

Spectrum (m)

0 100 200

0.5

1.5

Frequency (Hz)

Spectrum (rad)

38.0Hz

ab c

de f

Fig. 28.5 The displacement spectrum curves. (Node 2: (a)X;(b)Y;(c) ™ Node 3: (d)X;(e)Y;

(f) ™ Factor of random excitation: solid line 0.25; dashed line 0.5)

28 Nonlinear Self-Deﬁned Truss Element Based on the Plane Truss Structure 365

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

−2

−1

x 10

−4

x 10

−4

Time(s)

Position (m)Position (m)

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

−2

−1

Fig. 28.6 The position curves. (Node: (a) node 2; (b) node 3. Contact pair: solid line a; dashed

line b)

contact pair. In spite of two excitations with the different amplitudes, the position

curves at every node are almost synchronous, respectively. The other phenomenon is

that the repeated impact curves at the node 2 between the two boundaries are clearer

than those at the node 3. The possible explanation is that the node 2 is actively

excited, but the node 3 is passively excited.

28.4.2.2 Contact Stiffness

The dynamic responses are compared in the present example which the contact

stiffness is considered as 1.5E7 and 1.5E8N/m. A sine signal with the ﬁrst mode

frequency 38.0 Hz is adopted as the excited force. Moreover, the gain factors of F

and F

are 0.5 and 2.5 N, respectively.

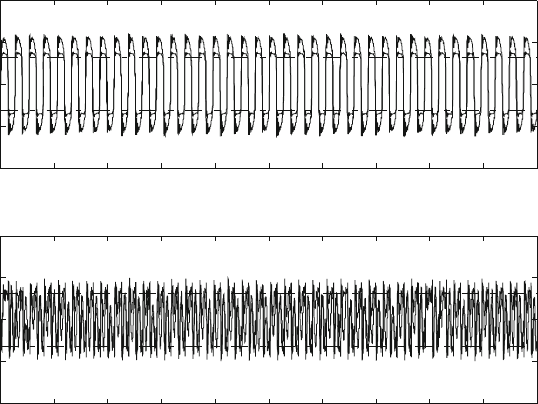
The curves of the displacement responses and the corresponding displacement

spectrums are given as shown in Figs. 28.7 and 28.8, respectively.

In Fig. 28.7, it can be seen that the contact stiffness has little effect on the axis

responses of the system, but it has obvious effect on the other two responses at

every nodes. From sub-ﬁgure (b, c, e, f), the smaller contact stiffness can result in

the greater response level. As shown in Fig. 28.8, the spectrum curves have several

peak values. And it is found that all the peak frequencies are several times of the

excited frequency. It is obvious that the nonlinear dynamic system has generated

366 Y. L u o e t a l .

0 0.5 1

x 10

−3

x 10

−3

Time (s)

Amplitude (m)

0 0.5 1

−4

−2

x 10

−4

x 10

−4

Time (s)

Amplitude (m)

0 0.5 1

−2

−1

x 10

−3

x 10

−3

Time (s)

Amplitude (rad)

0 0.5 1

−2

−1

Time (s)

Amplitude (m)

0 0.5 1

−4

−2

Time (s)

Amplitude (m)

0 0.5 1

−4

−2

Time (s)

Amplitude (rad)

def

−2

−1

Fig. 28.7 The displacement response curves. (Node 2: (a)X;(b)Y;(c) ™ Node 3: (d)X;(e)Y;

(f) ™ Contact stiffness: dashed line 1.5E7 N/m; solid line 1.5E8 N/m)

ab c

de f

0 200 400

Frequency (Hz)

Amplitude (m)

0 200 400

Frequency (Hz)

Amplitude (m)

0 200 400

Frequency (Hz)

Amplitude (m)

0 200 400

Frequency (Hz)

Amplitude (m)

0 200 400

0.5

1.5

Frequency (Hz)

Amplitude (m)

0 200 400

Frequency (Hz)

Amplitude (m)

38.0Hz

76.0Hz

Fig. 28.8 The displacement spectrum curves. (Node 2: (a)X;(b)Y;(c) ™ Node 3: (d)X;(e)Y;

(f) ™ Contact stiffness: dashed line 1.5E7 N/m; solid line 1.5E8 N/m)

28 Nonlinear Self-Deﬁned Truss Element Based on the Plane Truss Structure 367

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

x 10

−4

x 10

−4

Position (m)Position (m)

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

−4

−2

−4

−2

Time (s)

Fig. 28.9 The position curves. (Nodes: (a) node 2; (b) node 3. Contact stiffness: dashed line

1.5E7 N/m; solid line 1.5E8 N/m)

the primary resonance and the superharmonic resonance phenomenon. Moreover,

both of the displacement spectrum curves in sub-ﬁgure (a, d) have generated only

one superharmonic resonance at the frequency 76.0 Hz. But more superharmonic

resonances are observed in the other four sub-ﬁgures. This result reﬂects that the

nonlinear performance of the axis motion of the system is weaker than that of the

other two directions.

From Fig. 28.9, it can be observed that the position curves of the two nodes are vi-

brated around the up and below contact boundaries (as shown by dash-dot). Because

the excited forces are only actuated at the node 2, the position curves in Fig. 28.9a

have obvious periodicity compared with that in Fig. 28.9b. And an obvious phe-

nomenon is that the amplitude of the penetration is inversely proportional to the

contact stiffness.

28.4.2.3 Clearance

In this example, the contact stiffness is 1.5E8 N/m, the excited force is same so that

in the example of contact stiffness, and the clearance value is adopted two cases:

0m (without clearance) and 127 m (with clearance).

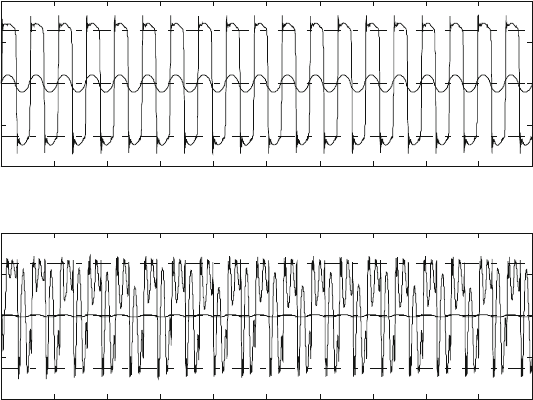
Figures 28.10 and 28.11 are given the displacement response curves and the cor-

responding spectrum curves. From Fig.28.10, it can be seen that the clearance has

368 Y. L u o e t a l .

0 0.5

−2

−1

x 10

−3

Time (s)

Amplitude (m)

0 0.5

−2

−1

x 10

−4

Time (s)

Amplitude (m)

0 0.5

−2

−1

x 10

−3

Time (s)

Amplitude (m)

0 0.5

−2

−1

x 10

−3

x 10

−3

Time (s)

Amplitude (m)

0 0.5

−2

−1

x 10

−4

Time (s)

Amplitude (m)

0 0.5

−2

−1

x 10

−3

Time (s)

Amplitude (m)

def

Fig. 28.10 The displacement response curves. (Node 2: (a)X;(b)Y;(c) ™ Node 3: (d)X;(e)Y;

(f) ™ Clearance: dashed line with; solid line without)

0 200 400

−1

−2

Frequency (Hz)

Amplitude (m)

−4

−6

−2

Amplitude (m)

−4

−6

−2

Amplitude (m)

−2

−4

Amplitude (rad)

−2

−4

Amplitude (rad)

−1

−2

Amplitude (m)

0 200 400

Frequency (Hz)

0 200 400

Frequency (Hz)

0 200 400

Frequency (Hz)

0 200 400

Frequency (Hz)

0 200 400

Frequency (Hz)

38.0Hz

76.0Hz

abc

def

Fig. 28.11 The displacement spectrum curves. (Node 2: (a)X;(b)Y;(c) ™ Node 3: (d)X;(e)Y;

(f) ™ Clearance: dashed line with; solid line without)

28 Nonlinear Self-Deﬁned Truss Element Based on the Plane Truss Structure 369

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

−2

−1

x 10

− 4

Time (s)

Position (m)Position (m)

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

x 10

− 4

−2

−1

Fig. 28.12 The position curves. (Nodes: (a) node 2; (b) node 3. Clearance: dashed line with; solid

line without)

little effect on the axis motion of the system by observing the sub-ﬁgure (a, d).

However, the clearance has great effect on the other responses by the obvious

different result in the sub-ﬁgure (b, c, e, f). The corresponding spectrum curves

also expressed the results as shown in Fig. 28.11. Only one hyperhormonic reso-

nance peak is observed in sub-ﬁgure (a, d), but a series of ones are observed in the

other four sub-ﬁgures. For the case of without clearance, the response curves and

spectrum curves become more regular and their amplitudes are also reduced sig-

niﬁcantly than that of with clearance as shown in Figs. 28.10 and 28.11b, c, e, f.

From Fig. 28.12, the penetration is always generated and the curve can be regarded

approximately as the sinusoidal curve when the clearance value is zero.

28.5 Conclusions

In this paper, a nonlinear ﬁnite-element model is developed to analyze the dynamic

problems of a new type plane truss structure with the ﬂexible connector that included

clearance, friction, and axial constraint based on the self-deﬁned truss element. And

then the model is solved by means of the nonlinear numerical solution method based

on the Newmark implicit integrate method together with Newton–Raphson intern

method. An example: single ﬂexible truss structure is also analyzed using the non-

linear numerical solution method.

370 Y. L u o e t a l .

There are two conclusions in the numerical example. On the one hand, the stiff-

ness level along axial direction is lower than the other directions, so that the ﬁrst

mode can be clearly observed only in the axial response for the case of random

excitation. On the other hand, both the contact stiffness and the clearance mainly

affect the responses of the two non-axial DOFs. And both of them induce the su-

perharmonic resonance phenomena. Obviously, the dynamic motion of the single

ﬂexible truss structure has strong nonlinearity.

In summary, the developed nonlinear self-deﬁned element represents the nonlin-

ear cases and the dynamic properties of the system well. In the future, the method

above will be thoroughly discussed in the complex plane truss structure.

Acknowledgments This work was supported by the Civil Space Advanced Project of China under

Grant No. C4120061309.

References

1. Tzou HS, Roog Y (1991) Contact dynamics of a spherical joint and a jointed truss-cell system.

AIAA J 29(1):81–88

2. Ferri AA (1998) Modeling and analysis of nonlinear sleeve joints of large space structures.

AIAA J Spacecr Rockets 25(5):354–360

3. Junjiro O, Tetsuni S, Kenji M (1995) Passive damping of truss vibration using preloaded joint

backlash. AIAA J 33(7):1335–1341

4. Bindemann AC, Ferri AA (1995) Large amplitude vibration of a beam restrained by a non-

linear sleeve joint. J Sound Vib 184(1):19–34

5. Hsu ST, Grifﬁn JH, Bielak J (1989) How gravity and joint scaling affect dynamic response.

AIAA J 27(9):1280–1287

6. Flores P, Ambr´osio J, Claro JCP, Lankarani HM (2008) Translational joints with clearance in

rigid multibody systems. J Comput Nonlinear Dyn 3(011007):1–10

7. Shi G, Atluri SN (1992) Nonlinear dynamic response of frame-type structures with hysteretic

damping at the joints. AIAA J 30(1):234–240

8. Gaul L, Lenz J (1997) Nonlinear dynamics of structures assembled by bolted joints. Acta Mech

125:169–181

9. Dubowsky S, Deck JF, Costello H (1987) Dynamic modeling of ﬂexible spatial machine

systems with clearance connections. J Mech Transm Autom Des 109(1):87–94

10. Lankarani HM, Nikravesh PE (1990) A contact force model with hysteresis damping for impact

analysis of multibody systems. ASME J Mech Des 112:369–376

11. Lankarani HM, Nikravesh PE (1994) Continuous contact force models for impact analysis in

multibody systems. Nonlinear Dyn 5:193–207

12. Yigit AS, Ulsoy AG, Scott RA (1990) Spring-dashpot models for the dynamics of a radially

rotating beam with impact. J Sound Vib 142(3):515–525

Chapter 29

Complex Frequency Analysis of an Axially

Moving String with Multiple Attached

Oscillators by Using Green’s Function Method

Le-Feng L¨u, Yue-Fang Wang, and Ying-Xi Liu

Abstract In the present paper, the eigenvalue problem of an axially moving string

with multiple attached mass-spring oscillators is investigated. Closed form transcen-

dental equations for the natural frequencies are obtained by means of the Green’s

function method. The maximum variance rate of eigen-frequencies of the string is

presented to indicate the coupling strength between the modes of subsystems. The

Galerkin’s discretization method is analyzed so as to determine the approximate

eigenvalues for large numbers of oscillators. The results of the traveling mass model

are also presented as a limit case.

29.1 Introduction

Axially moving continuum, rotating ﬂexible machineries, and ﬂuid-conveying pipes

are examples of gyroscopic systems. A convective acceleration component in the

governing equations renders complex, speed-dependent modes. In ﬁnding the eigen-

solution of this problem, Meirovitch [1, 2] proposed a method for the solution of

the eigenvalue problem for linear gyroscopic systems, which permits a formulation

in terms of real symmetric matrices. Parker [3] adopted a perturbation analysis

to determine approximate eigenvalue loci for axially moving materials on elastic

foundation. Wang et al. [4] investigated the eigenvalue problem for axially moving

strings based on Hamilton system and obtained the modal functions and symplectic

orthogonality conditions through a symplectic analysis.

For those continuous system subjected to complex constraints the system char-

acteristics can be signiﬁcantly inﬂuenced by the coupling between subsystems.

For example, for moving oscillator systems the presence of mass-spring oscillator

Y. - F. Wa n g (



)

Department of Engineering Mechanics, Dalian University of Technology, 2 Linggong Road,

Dalian 116024, People’s Republic of China

and

State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian 116024,

People’s Republic of China

e-mail: yfwang@dlut.edu.cn

A.C.J. Luo (ed.), Dynamical Systems: Discontinuity, Stochasticity and Time-Delay,

DOI 10.1007/978-1-4419-5754-2

29,

 Springer Science+Business Media, LLC 2010

371

372 L.-F. L¨uetal.

varies the inertia of the system, which results in location-dependent eigenvalues

that are different from conventional analytical eigenvalue solutions. Stannisie [5]

determined exact eigen-solutions for mass moving on an elastic foundation by per-

forming the integration in the Stieltjes sense. Kukla [6, 7] studied the eigenvalue

problem of a beam with intermediate elastic supports and presented the exact so-

lution of the coupled system by means of Green’s function method. The Green’s

function, with its intuitive concept and deﬁnite physical meaning, is simple yet ef-

fective for problems with presence of Dirac-Delta function. From the point of view

of the Green’s function theory, reference [5] utilizes the properties of Green’s func-

tion that was equivalent to the method of [6,7].

The Green’s function method is used to analyze the eigenvalue problem for the

axially moving string with attached mass-spring oscillator in this paper. The theorem

of construction of Green’s function is applied to obtain the explicit Green’s function

of the coupling system without complicated computation. In the numerical demon-

stration, the maximum variance rate of the eigen-frequencies of the moving string

related to coupling strength between the string and the masses is calculated. The

model of attached mass is also analyzed as the limit case of the coupled oscillator.

Finally, the Galerkin’s method is compared with the Green’s function method for

validity of the Galerkin’s discretization method.

29.2 Formulation of the Eigenvalue Problem

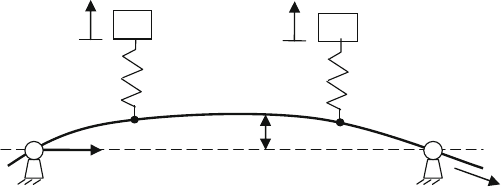
Consider a simply supported, axially moving string travelling with a velocity c with

N attached undamped linear oscillators, as shown in Fig. 29.1. Assume the i th os-

cillator arrives at the left end of the string at time t

;i D 1;:::;N,ofwhichthe

coefﬁcient of acting time is „

D H.t  t

/  H.t  .t

C 1=c//,whereH./ is the

Heaviside unit-step function. By neglecting the ﬂexural, shear, and torsion rigidity,

the nondimensional governing equations of transverse vibration of the system can

be written in the form [8]

(t)

(x,t)

Fig. 29.1 Axially moving string with attached multiple oscillators

29 Complex Frequency Analysis of an Axially Moving String 373

Rw C . Pw C cw

/ C 2c Pw

C .c

 1/w

iD1

„

 w/ı.x  x

/ C f

;

(29.1)

 w.x

;t// D f

 t  t

C 1=c; i D 1;:::;N; (29.2)

where w.x; t/ is the transverse displacement of the string,  the modal damping of

the string, y

and m

the deﬂection, the stiffness coefﬁcient and mass of the

ith oscillator, respectively. f

and f

are external forces on the string and mass,

respectively. ı./ is the Dirac-Delta function.

Let the general solutions of the foregoing be

w.x; t/ D Ref.x/e

t

g;y

.t/ D Y

t

; (29.3)

which leads to an eigenvalue problem

1/

.x/ C.2c Cc/

.x/ C.

C/.x/ D

iD1

.x

/„

ı.x  x

(29.4)

where "

D m



=.m



C k

By applying the Green’s function method, the solution of (29.4) can be obtained,

.x/ D

iD1

„

.x

/ı.x  x

/G.xI/d D

iD1

„

.x

/G.xIx

(29.5)

where G.xI/ is the Green’s function of the (29.4).

AsetofN homogeneous equations can be derived by substituting x D x

;iD

1;:::;N into (29.5), yielding

.x

/ C

j D1

„

.x

/G.x

/ D 0; i D 1;:::;N: (29.6)

The following equation must hold to require a non-trivial solution of (29.6):

„

G.x

/ C 1"

„

G.x

/  "

„

G.x

„

G.x

„

G.x

/ C 1  "

„

G.x

„

G.x

„

G.x

/  "

„

G.x

/ C 1

D 0:

(29.7)