Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay
Подождите немного. Документ загружается.

30 Reduction on Inertial Manifolds of Navier–Stokes Equations 385
On the other hand, it is well known that the asymptotic behaviors of some higher
dimensional or even infinite dimensional dissipative dynamic systems evolve to a
compact set known as a global attractor, which is finite-dimensional [13]. That
means such kind of dynamic systems can be described by the deterministic flow
on a lower dimensional attractor. Hence, it opens the way for the reduction of the
dynamics of infinite-dimensional dissipative equations to finite-dimensional sys-
tems, or higher dimensional dissipative equations to a lower dimensional system.
Consequently, various schemes have been used to construct a finite system for re-
producing the asymptotic dynamics of the original dynamic system [14–19]. One
of the schemes is the traditional Galerkin method, which ignores the small spatial
structure of a solution. However, an important and well-known aspect of nonlin-
ear dynamics is the sensitive dependence of the solution on the perturbations. Such
perturbations include small variations in initial and boundary values, as well as nu-
merical errors if a numerical computation method is adopted. A slight perturbation
to the system may produce very important effects and significant changes in the
system’s configuration after a long time [20]. The Center Manifold Theory can be
applied to the system with a small number of modes, whose eigenvalues are close
to the imaginary axis, but a small parameter variation from the critical value or a
large parameter variation for some cases will have the effect that additional modes
will become unstable, and the originally low dimensional system will not be valid
anymore [1].
The theory of Inertial Manifolds (IMs) has shown that the long time dynamic
behaviors of dissipative partial differential equation (PDE) can be fully described
by that of a set finite ordinary differential equation to which the PDE is reduced
on IMs. Roughly speaking, the IMs can be considered as a reduction method. In
fact, the methods used to construct the IMs are the adaptations of various theo-
ries in the studies of center manifolds and integral manifolds. Then, the stability
and bifurcation can be investigated based on the ordinary differential equation with
relatively low dimension on the IMs, and some nature of nonlinear phenomena can
be explained availably and feasibly.
For decades, the theory of Inertial Manifolds is a novel technique for model re-
duction [1, 21–23]. Unfortunately, the existence of IMs usually holds only under
the very restrictive spectral gap condition. Hence in practical applications, the con-
cept of Approximate Inertial Manifolds (AIMs) has been introduced [12, 23, 24].
However, there are few studies on the IMs and AIMs for the second order in time
nonlinear dissipative autonomous dynamic systems. In [25], AIMs for second order
in time partial differential equations with delay are constructed, and some impor-
tant results have been given. In light of Approximate Inertial Manifolds developed
in infinite dynamic systems and Mode Analysis in linear structural dynamics, a
combined method is presented to reduce the second order in time nonlinear dis-
sipative autonomous dynamic systems with many degrees-of-freedom, which are
encountered frequently in engineering, and the influence of model reduction on
the long-term behaviors has been studied in detail, and the error estimate is also
given [26]. Additionally, the AIMs has been introduced to the dynamic snap-through
buckling analysis of shallow arches under impact load [27].
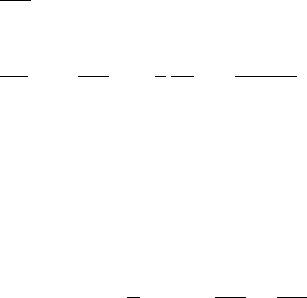
386 J.-Z. Zhang et al.
In this study, following Optimum finite element nonlinear Galerkin algorithm for
the Navier–Stokes equations [28], the multilevel finite element method is adapted
to approach the AIMs for Navier–Stokes equations, and the governing equations
can be projected onto the space dominated by the Inertial Manifolds, which is finite
dimension.
30.2 Multilevel Finite Element Method
For the sake of simplicity, the Approximate Inertial Manifolds approached by mul-
tilevel finite element method is given for the incompressible flow. The governing
equations with elementary variables for the incompressible flow are
8
ˆ
ˆ
ˆ
ˆ
<
ˆ
ˆ
ˆ
ˆ
:
@u
j
@x
j
D 0
@u
i
@t
C u
j
@u
i
@x
j
D
1
@p
@x
i
C
@
2
u
i
@x
j
@x
j
.i D 1; 2/: (30.1)
The boundary conditions:
D
1
[
2
;
where
1
is boundary for the velocity,
2
the essential boundary condition for the
pressure. And on boundary
1
, u
i
DQu
i
.i D 1; 2/, on boundary
2
p
ij
n
j
D
Qp
i
.i D 1; 2/, n
j
is the outward normal unit vector component on
2
, and tensor
p
ij
D
p
ı
ij
C
@u
i
@x
j
C
@u
j
@x
i
:
The initial conditions:
u.x
i
;0/ D u
0
.x
i
/:
In a sense, the nonlinear phenomena are the features of the interaction between the
higher mode and the lower mode in the system. The nonlinear Galerkin method
is the new numerical method for the computational fluid dynamics. Following the
Inertial Manifolds and the nonlinear dynamics, and it decomposes the unknown
into two components, that is, the large eddy and small eddy, the essential interaction
between them is the key for the schemes. For spectral method, such two components
are approached by the two subspaces spanned by the Eigen functions of the positive
definite operator. For the finite element methods, such kind subspaces are spanned
by a coarse grid finite element space and a fine grid incremental finite element space.
For the coarse grid finite element space, the quadrangle element is adopted to
mesh the domain, as shown in Fig. 30.1.
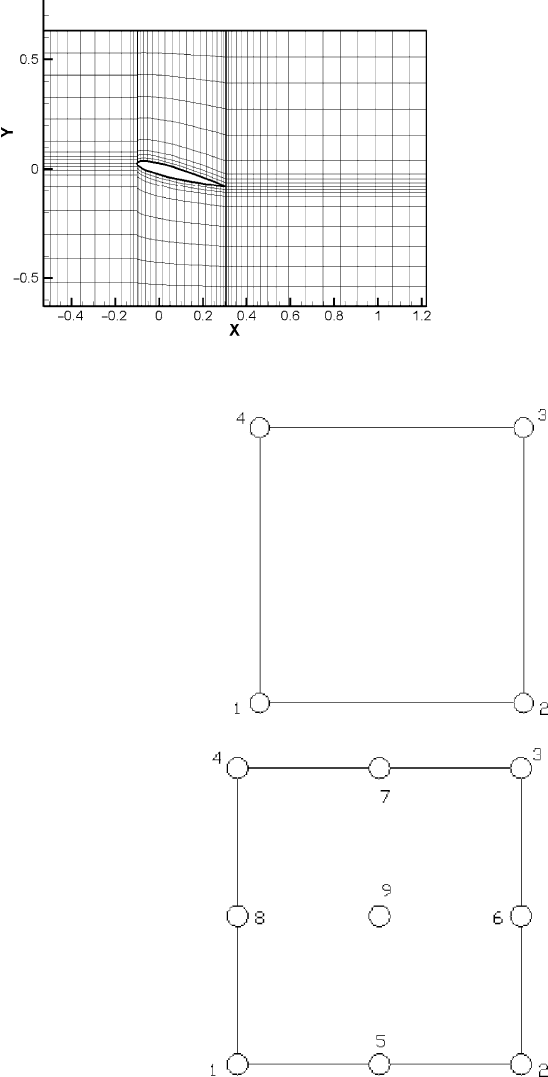
A quadrangle element with four nodes, namely, initial element, is shown in
Fig. 30.2 as the initial mesh, and then it is refined by adding other five nodes,
resulting in a refined quadrangle element with nine nodes, as shown in Fig. 30.3.Itis
30 Reduction on Inertial Manifolds of Navier–Stokes Equations 387
Fig. 30.1 The mesh of the domain
Fig. 30.2 Quadrangle
element with four nodes
Fig. 30.3 Quadrangle
element with nine nodes

388 J.-Z. Zhang et al.
clear that node 1, 2, 3, 4 in Fig. 30.3 are the same as that in Fig. 30.2, and hence such
element is referred to as multilevel element by this regular refinement for the mesh.
Accordingly, the shape function is constructed in the initial element, and the ba-
sis functions span the fundamental finite element space. Further, the shape function
is constructed with the other five nodes to provide the basis function for the incre-
mental finite element space.
For clarity, the shape functions for the quadrangle element with four nodes are
listed as follows,
N
1
D
1
4
.1 /.1 / N
2
D
1
4
.1 C /.1 /;
N
3
D
1
4
.1 C /.1 C / N
4
D
1
4
.1 /.1 C /:
As for the quadrangle element with nine nodes, the hierarchical functions for the
variable u can be presented as the following, remaining the fundamental shape func-
tions unchanged,
H
1
D N
1
H
2
D N
2
H
3
D N
3
H
4
D N
4
N
H
5
D
1
12
.
3
/.1 /
N
H
6
D
1
12
.1 C /.
3
/
N
H
7
D
1
12
.
3
/.1 C /
N
H
8
D
1
12
.1 /.
3
/
N
H
9
D
1
12
.
3
/.
3
/:
Following the Inertial Manifolds, the velocity in the element, namely, u
.e/
, can be
decomposed into
u
.e/
D y
.e/
C z
.e/
;
where y
.e/
denotes the large eddy component, z
.e/
the small eddy component. More,
the following expressions can be obtained
y
.e/
D
4
X
iD1
N
i
y
.e/
i
; z
.e/
D
9
X
iD5
N
H
i
z
.e/
i
:
30.3 The Weak Form of the Navier–Stokes Equations
Following the Galerkin procedure, the weak form of the governing equations for
incompressible flow can be obtained as
Z
@u
j
@x
j
ıp d D 0 (30.2)

30 Reduction on Inertial Manifolds of Navier–Stokes Equations 389
Z
@u
i
@t
C u
j
@u
i
@x
j
C
1
@p
@x
i
@
2
u
i
@x
j
@x
j
ıu
i
d D 0 (30.3)
By the Green formulas, (30.2) can be rewritten as
Z
u
j
@
@x
j
.ıp/d D
Z
1
Nu
n
ıp d (30.4)
where Nu
n
is the norm component on
1
,
Nu
n
DNu
j
Nn
j
:
Similarly, (30.3) can be rewritten as the following form,
Z
@u
i
@t
C u
j
@u
i
@x
j
ıu
i
C
p
ı
ij
C
@u
i
@x
j
C
@u
j
@x
i
@
@x
j
.ıu
i
/
d D
Z
2
Np
i
ıu
i
d
(30.5)
The terms in the left hand side in (30.5) denotes the inertial force, normal stress, vi-
sual power from viscosity, respectively. And the terms in the right hand side denotes
the visual power both from outer forces on the boundary and mass force.
30.4 Numerical Methods
The pressure-correctionmethod is applied to the numerical analysis of the governing
equations. The Euler scheme is used to approach the derivative
8
ˆ
ˆ
ˆ
ˆ
ˆ
<
ˆ
ˆ
ˆ
ˆ
ˆ
:
@u
.nC1/
j
@x
j
D 0
Ou
.nC1/
i
u
.n/
i
t
C u
.n/
j
@u
.n/
i
@x
j
D
1
@p
.nC1/
@x
i
C
@
2
u
.n/
i
@x
j
@x
j
.i D 1; 2I n is the time step/
(30.6)
For such implicit scheme, an intermediate velocity Ou is introduced availably, and the
momentum equations can be rewritten as the following form,
Ou
i
u
.n/
i
t
C u
.n/
j
@u
.n/
i
@x
j
D
1
@p
.n/
@x
i
C
@
2
u
.n/
i
@x
j
@x
j
.i D 1; 2I n is the time step/
(30.7)
However, the variable p is explicit in the scheme, and its value can be set as that at
the last step. Subtracting (30.6) from (30.7)gives,
u
.nC1/
i
Ou
i
D
t
@p
.nC1/
@x
i
@p
.n/
@x
i
!
(30.8)

390 J.-Z. Zhang et al.
A scalar variable is also introduced, and let
u
.nC1/
i
Ou
i
D
@
@x
i
(30.9)
The pressure p at the next step can be expressed
p
.nC1/
D
t
C p
.n/
(30.10)
Following the divergence of (30.9) and the continuity equation, a Poisson equation
relevant to can be given as
@
2
@x
2
1
C
@
2
@x
2
2
D
@Ou
1
@x
1
C
@Ou
2
@x
2
(30.11)
Then, can be obtained from (30.11), and substitute it into (30.9)and(30.10), both
u and p can be solved together.
30.5 Large Eddy and Small Eddy Components
As stated above, the velocity in the domain can be decomposed into large eddy and
small eddy components, namely, u D y C z. In the element, the velocity can be
expressed as
u
.e/
D y
.e/
C z
.e/
D
X
H
i
y
.e/
i
C
X
N
H
i
z
.e/
i
:
Similarly, the pressure in the element can be expressed as
p
.e/
D
X
i
P
.e/
i
C
X
N
i
Np
.e/
i
:
The weight function in (30.5) can be chosen as ıu
i
,andsetıu
i
D
N
H
j
(j D
5; 6; : : :; 9). As for (30.4), set ıp D
N
‰
k
(k D 5; 6; : : :; 9). Equations (30.4)and
(30.5) can be rewritten consequently as
A
.e/
Pz
.e/
1
C B
.e/
z
.e/
1
z
.e/
1
C C
.e/
z
.e/
2
z
.e/
1
C D
.e/
1
Np
.e/
C F
.e/
1
z
.e/
1
C F
.e/
2
z
.e/
2
D E
.e/
1
A
.e/
Pz
.e/
2
C B
.e/
z
.e/
1
z
.e/
2
C C
.e/
z
.e/
2
z
.e/
2
C D
.e/
2
Np
.e/
C F
.e/
3
z
.e/
1
C F
.e/
4
z
.e/
2
D E
.e/
2
M
.e/
1
z
1
C M
.e/
2
z
2
D G
.e/

30 Reduction on Inertial Manifolds of Navier–Stokes Equations 391
Furthermore, the final governing equations can be expressed in the following form,
APz
1
C Bz
1
z
1
C C z
2
z
1
C D
1
Np C F
1
z
1
C F
2
z
2
D E
1
(30.12)
APz
2
C Bz
1
z
2
C C z
2
z
2
C D
2
Np C F
3
z
1
C F
4
z
2
D E
2
(30.13)
M
1
z
1
C M
2
z
2
D G (30.14)
It is clear that the relationship between y
i
and z
i
can be expressed in the implicit
form by (30.12)and(30.13), that is, coefficients are the function of y
i
.Asy
i
is
known, z
i
can be obtained from this relationship.
Also, the Euler scheme is used to approach the derivative in time,
Pu
˛r
D
u
.iC1/
˛r
u
.i/
˛r
t
.˛ D 1; 2I r D 1;2;:::;N
u
/:
At t D t
iC1
, the implicit scheme is chosen as the following,
Az
.iC1/
1
C t
Bz
.iC1/
1
z
.iC1/
1
C Cz
.iC1/
2
z
.iC1/
1
C D
1
Np
.iC1/
C F
1
z
.iC1/
1
C F
2
z
.iC1/
2
D tE
1
C Az
.i/
1
Az
.iC1/
2
C t
Bz
.iC1/
1
z
.iC1/
2
C Cz
.iC1/
2
z
.iC1/
2
C D
2
Np
.iC1/
C F
3
z
.iC1/
1
C F
4
z
.iC1/
2
D tE
2
C Az
.i/
2
As z
.i/
at i step is known, z
.iC1/
can then be obtained from the iterative following
Newton–Raphson method,
J
.iC1/;.k/
x
.iC1/;.kC1/
D J
.iC1/;.k/
x
.iC1/;.k/
R
.iC1/;.k/
where
x D
2
4
z
1
z
2
Np
3
5
:
The residual is
R D
2
4
R
1
R
2
R
3
3
5
:
Herein, J is the Jacobean Matrix.
392 J.-Z. Zhang et al.
30.6 Numerical Examples
The NACA0012 airfoil is analyzed as a numerical example. The parameters of the
systems can be listed as
Kinematic viscosity of air D 1:8 10
5
Ns=m
2
, density D 1:205 kg=m
3
,
chord length c D 0:42 m, freestream velocity u D 100 m=s.
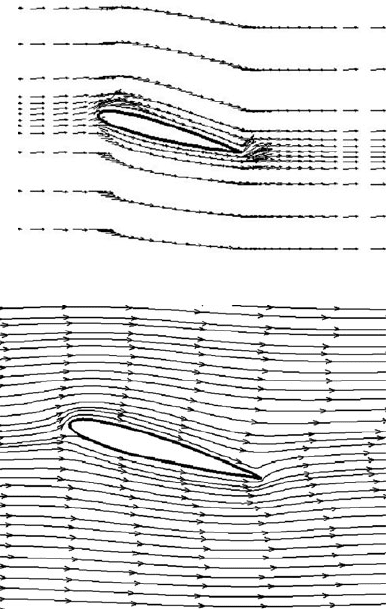
Figures 30.4–30.6 are the results of the flow field using coarse mesh, and it is
clear that there is no vortex in the boundary layer. As the small eddy components
are considered, that is, the Approximate Inertial Manifolds is used to approach
the solution of the system, some detail features of the system can be captured.
Figures 30.7–30.9 are the results from multilevel finite element method. Referring
to Fig. 30.10, it can be seen that the Approximate Inertial Manifolds can capture
the small eddies in the boundary layer, in comparison with the traditional Galerkin
method. It is well-known that such small eddies in the boundary layer is very
important for the flow control in the engineering.
Fig. 30.4 Velocity of the
flow from the traditional
method
Fig. 30.5 Streamline of the
flow from the traditional
method

30 Reduction on Inertial Manifolds of Navier–Stokes Equations 393
Fig. 30.6 Pressure
distribution from traditional
method
Fig. 30.7 Velocity of the
flow from AIMs
Fig. 30.8 Streamline of the
flow from AIMs

394 J.-Z. Zhang et al.
Fig. 30.9 Pressure
distribution from AIMs
Fig. 30.10 Streamline of the
flow from [29]
30.7 Concluding Remarks
In comparison with the traditional methods, the Approximate Inertial Manifolds
approached by the multilevel finite element method is feasible for the numerical
analysis of complex flow, and much computing time can be saved with an accurate
result. In particular, following Approximate Inertial Manifolds, the solution space
can be decomposed into two subspace, namely, large eddy and small eddy compo-
nents, and the method can capture the small eddies and a more accurate solution
can be given. In sense of dynamics, the Approximate Inertial Manifolds can be
considered as efficient method for model reduction for the nonlinear continuous
dynamic systems. As the further work, some improvements will be developed for
the numerical results.
Acknowledgments This research is supported by Program for New Century Excellent Talents in
University in China, No. NCET-07-0685.
